Содержание
Задача 1. 3
Задача 2. 4
Задача 4. 6
Задача 5. 9
Задача 6. 11
Задача 7. 14
Задача 9. 15
Задача 11. 19
Задача 13. 22
Список используемой литературы.. 25
Задача 1
Полуфабрикаты поступают на предприятие в виде листов фанеры. Всего имеется две партии материала, причем первая партия содержит 400 листов, а вторая – 250 листов. Из поступающих листов фанеры необходимо изготовить комплекты, включающие 4 детали 1 вида, 3 детали 2 вида, и 2 детали 3 вида. Лист фанеры каждой партии может раскраиваться различными способами. Количество деталей каждого типа, которое получается при раскрое одного листа соответствующей партии по тому или иному способу раскроя, представлено в таблице. Требуется раскроить материал так, чтобы обеспечить изготовление максимального числа комплектов.
| Первая партия |
Вторая партия |
| Детали |
Способ раскроя |
Детали |
Способ раскроя |
| 1 |
2 |
3 |
1 |
2 |
| 1 |
0 |
6 |
9 |
1 |
6 |
5 |
| 2 |
4 |
3 |
4 |
2 |
5 |
4 |
| 3 |
10 |
16 |
0 |
3 |
8 |
0 |
Решение
Обозначим через хij
число единиц из i-й партии (1,2) фанеры, которые намечено раскроить j -м способом (1,2,3) , так что из i-й партии при j-м способе раскроя будет получено аijk
хij
деталей к -го вида. Всего из всей i-й партии деталей к -го вида будет получено 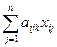 , а из всех mпартий их будет получено: , а из всех mпартий их будет получено: 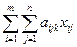
Из первой партии фанеры:
Деталей первого вида: 400(0х11
+6х12
+9х13
)
Деталей второго вида: 400(4х11
+3х12
+4х13
)
Деталей третьего вида: 400(10х11
+16х12
+0х13
)
Из второй партии фанеры:
Деталей первого вида: 250(6х21
+5х22
)
Деталей второго вида: 250(5х21
+4х22
)
Деталей третьего вида: 250(8х21
+0х22
)
Всего из двух партий фанеры:
Деталей первого вида: 400(6х12
+9х13
)+ 250(6х21
+5х22
)
Деталей второго вида: 400(4х11
+3х12
+4х13
)+ 250(5х21
+4х22
)
Деталей третьего вида: 400(10х11
+16х12
)+ 2000х21
Число полных комплектов, которое можно выпустить по данному плану, будет равно:
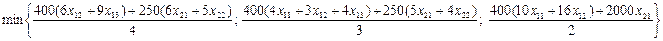 Введем дополнительную переменную х – отходы при используемом способе раскроя. В результате, получим задачу линейного программирования: Введем дополнительную переменную х – отходы при используемом способе раскроя. В результате, получим задачу линейного программирования:
z = x →min,
 при ограничениях: при ограничениях:
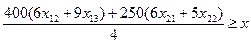
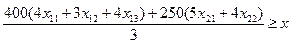
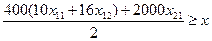
х11
+х12
+х13
=400
х21
+х22
+х23
=250
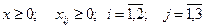 , где х, хij
– целые числа. , где х, хij
– целые числа.
Задача 2
Решить графическим методом.
Решить графическим методом
Z= 3 х1
-4х2
→ max при условиях:
-х1
+х2
≤1
-х1
+2х2
≥-2
х1
+х2
≥-1
-3х1
+2х2
≤6;
2х1
– х2
≤2
х1
≥0; х2
≥0
Решение
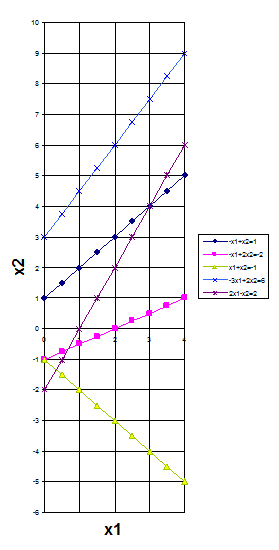
Запишем ограничения в виде равенств и построим соответствующие им линии уровня в системе координат. Строим область допустимых значений решения, удовлетворяющую начальным условиям. Семи заданным неравенствам соответствует множество точек плоскости, образующие пятиугольник АВСDE. Неравенства х1
≥-4; х1
+5х2
≥4 могут быть исключены, так как они определяют граничные прямые, не имеющие с АВСDE общих точек.
Строим на плоскости вектор целевой функции 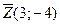 . Через начало координат перпендикулярно . Через начало координат перпендикулярно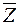 проводим линию уровня целевой функции Z=0. Линия уровня перемещается в направлении проводим линию уровня целевой функции Z=0. Линия уровня перемещается в направлении 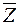 параллельно самой себе, пока не встретится с вершиной области допустимых значений АВСО т. В. Значение Z в точке В является минимальным. параллельно самой себе, пока не встретится с вершиной области допустимых значений АВСО т. В. Значение Z в точке В является минимальным.
При дальнейшем перемещении линия уровня пройдет через другую вершину ОДР, выходя из области решений – точку С. Значение Z в точке С является максимальным. Значение целевой функции Zm
ах
в т. С. Найдем её координаты:
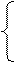 2х1
– х2
=2 2х1
– х2
=2
х2
=0
С(0; 1)
Zm
ах
=3*1-4*0=3
Ответ: Zm
ах
=3.
 Задача 4
Удельные затраты Сij
на перевозку 1 т груза вида i транспортом j (руб.) представлены матрицей
Сij
=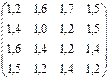
Мощности поставщиков А1
=30 тыс.т; А2
=10 тыс.т; А3
=40 тыс.т; А4
=70 тыс.т. Спрос потребителей: В1
=30 тыс.т; В2
=10 тыс.т; В3
=20 тыс.т; В4
=10 тыс.т.
Определить объемы перевозок груза транспортом j (руб.), чтобы суммарные издержки были бы минимальными, построить матрицу объемов перевозок.
Решение
1. Определяем тип задачи. Так как 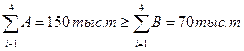 . Задача является открытой. Введем фиктивного потребителя с объемом потребления Вф
. . Задача является открытой. Введем фиктивного потребителя с объемом потребления Вф
.
2. Строим расчетную матрицу с фиктивным потреблением Вф
и удельными затратами на перевозку фиктивного груза Сi
ф
=0.
3. Сформируем опорный план по критерию наименьших удельных затрат на перевозку единицы груза , т. е. min Сi
ф.
Оставшиеся мощности относятся к фиктивному потребителю: хi
ф
=Аii
-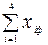
Опорный план
| В1
=30 тыс.т |
В2
=10 тыс.т |
В3
=20 тыс.т |
В4
=10 тыс.т |
Вф
|
Ui
|
| А1
=30 тыс.т |
1,2
3
0
|
1,6 |
1,7 |
1,5
0
|
0
|
1,5 |
| А2
=10 тыс.т |
1,4 |
1
10
|
1,2 |
1,5 |
0 |
1 |
| А3
=40 тыс.т |
1,6 |
1,4 |
1,2
20
|
1,4 |
0
2
0
|
1,2 |
| А4
=70 тыс.т |
1,5 |
1,2
0
|
1,4 |
1,2
1
0
|
0
6
0
|
1,2 |
| Vj
|
1,2 |
1,2 |
1,2 |
1,2 |
0 |
4. Проверим полученный план перевозок на вырожденность. Так как
4 столбца + 5 строк-1 > 7 поставок. То задача вырожденная. Для приведения плана к невырожденному состоянию введем в клетки (4;2) и (1,4) фиктивные нулевые поставки.
5. Оптимизируем план, используя метод потенциалов.
Сij
=Ui
+ Vj
, где Ui
– потенциал строки; Vj
– потенциал столбца.
Пусть V4
=0. пересчитаем все остальные Ui
и Vj
и зафиксируем их в опорном плане. U4
=1,2; Vф
=0; V4
=0-1,2=-1,2; Vф
=0-1,2=-1,2; U3
=0-(-1,2)=1,2; V3
=1,2-1,2=0; U1
=1,5-0=1,5; V1
=1,2-1,5=-0,3; V2
=0; U2
=1-0=1.
6. Определяем характеристики свободных клеток: Еij
= Сij
-(Ui
+ Vj
)≥0.
Е12
=1,6-0-1,5=0,1; Е13
=1,7-0-1,5=0,2; Е1ф
=1,2-1,5=-0,3; Е21
=1,4+0,3-1=0,7; Е23
=1,2-1=0,2; Е24
=1,5-1=0,5; Е2ф
=0+1,2-1=0,2; Е31
=1,6+0,3-1,2=0,7; Е32
=1,4-0-1,2=0,2; Е34
=1,4-0-1,2=0,2; Е41
=1,5+0,3-1,2=0,5; Е43
=1,4-0-1,2=0,2.
7. Характеристики клеток (3,ф) и (4,2) отрицательны, следовательно найденное решение не является оптимальным. Оптимизируем план. Для клетки к (1,ф) строим контур перераспределения.
х1ф
= min{0; 60}=60
Перенесем полученные результаты в новый план перераспределения.
| В1
=30 тыс.т |
В2
=10 тыс.т |
В3
=20 тыс.т |
В4
=10 тыс.т |
Вф
|
Ui
|
| А1
=30 тыс.т |
1,2
3
0
|
1,6 |
1,7 |
1,5
|
0
0
|
1,5 |
| А2
=10 тыс.т |
1,4 |
1
10
|
1,2 |
1,5 |
0 |
1 |
| А3
=40 тыс.т |
1,6 |
1,4 |
1,2
20
|
1,4 |
0
2
0
|
1,2 |
| А4
=70 тыс.т |
1,5 |
1,2
0
|
1,4 |
1,2
1
0
|
0
6
0
|
1,2 |
| Vj
|
1,2 |
1,2 |
1,2 |
1,2 |
0 |
Характеристики свободных клеток матрицы неотрицательны, следовательно найденное решение является оптимальным.
Задача решена.
Определим значение целевой функции:
F=30*1,2+10*1+20*1,2+1,2*10=82 (тыс.р.)
Задача 5
Для расчета мощности i-го вида транспорта необходимо воспользоваться значениями: S= 2 смены; z=8 часов; d= 25 дней.
Представлена грузоподъемность транспорта Р1
=10т; Р2
=5т; Р3
=10т; Р4
=15т.
АТП располагает m=4 видами транспортных средств различной грузоподъемности. Их количество n1
=20; n2
=30; n3
=30; n4
=20. На j-й вид продукции приходится Вj(m) спрос: В1
= 120 тыс.р.; В2
= 50 тыс.р.; В3
= 80 тыс.р.; В4
= 100 тыс.р. Известно, что среднее время транспортировки для каждого вида транспорта и вида груза:
Т=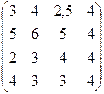
Даны себестоимости перевозок j-го груза i-ым видом транспорта.
С=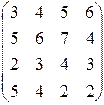
Определить такие объемы перевозок, чтобы суммарные месячные издержки перевозок были бы минимальными.
Решение
1. Определяем мощность Аi
=dtSni
d– количество рабочих дней (d=25) в месяце;
t – количество часов в смене (t=8);
S– количество смен (S=2) в сутки
ni
– количество машин i-го типа.
А1
=25*8*2*20=8000 маш.ч.; А2
=25*8*2*30=12000 маш.ч.; А3
=12000 маш.ч.; А4
=8000 маш.ч.
2. Рассчитаем показатель удельной производительности (т/маш.ч.); λij
=Pi
/tij
.
λ=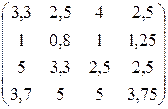
3. Рассчитаем критерий формирования опорного плана: kij
= λij
/ Сij
.
K=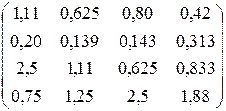
4. Строим опорный план перевозок, клетки распределения выбираем по maxkij
.
Это клетки Х31
и Х43.
Расчетная матрица
| В1
= 120 тыс.р. |
В2
= 50 тыс.р. |
В3
= 80 тыс.р. |
В4
= 100 тыс.р. |
Ui
|
| А1
=8 тыс.р. |
3 3,3
8
|
4 2,5
|
5 4
|
6 2,5
|
3 |
| А2
=12 тыс.р. |
5 1 |
6 0,8 |
7 1 |
4 1,25
12
|
4 |
| А3
=12 тыс.р. |
2 5
12
|
3 3,33
|
4 2,5
|
3 2,5 |
2 |
| А4
=8 тыс.р. |
5 3,7 |
4 5 |
2 5
8
|
2 3,75 |
2 |
| Аф
|
0 1
33,3
|
0 1
50
|
0 1
40
|
0 1
85
|
0 |
| Vj
|
0 |
0 |
0 |
0 |
5. Итак, все мощности использованы, но не все потребности удовлетворены – введем фиктивный вид транспорта (строка) с Сi
ф
=0 и λi
ф
=1. произведем расчет фиктивных поставок.
6. Проверяем план на вырожденность:
5 строк + 4 столбца -1=8 поставок. Задача невырожденная.
Оптимизируем опорный план.
Определяем потенциалы строк и столбцов по выражению:
Сij
= Ui
+Vj
λij
, откуда Ui
= Сij
-Vj
λij
; Vj
= (Сij
-Ui
)/λij
Зададимся потенциалом фиктивной троки: Uф
=0.
Тогда: V3
=V2
= V1
= V4
=0; U4
=4-5∙0=4; U3
=2-0=2; U2
=4-0=4; U1
=3-0=3
Определяем характеристики свободных клеток по формуле:
Еij
= Сij
-(Ui
+ λij
Vj
);
Е12
=4-3-0>0; Е13
=5-3-0>0; Е14
=6-3-0>0; Е21
=5-4-0>0; Е22
=6-4>0; Е23
=7-4>0; Е32
=3-2>0; Е33
=4-2>0; Е34
=3-2>0; Е41
=5-2>0; Е42
=4-2>0; Е44
=2-2=0.
Так как все Еij
≥0, то план оптимальный (но не единственный, так как Е44
=0)
Целевая функция затрат на перевозку:
F=8*3+12*4+12*2+8*2=112 (тыс.р.)
Задача 6
Для обслуживания потребителей предприятие может выделить 3 вида транспорта А1
, А2
, А3,
получая прибыль, зависящую от спроса на них (В1,
В2,
В3
).
| В1
|
В2
|
В3
|
В4
|
| А1
|
1 |
3 |
3 |
2 |
| А2
|
4 |
2 |
0 |
2 |
| А3
|
3 |
1 |
0 |
1 |
    Определить оптимальную пропорцию транспортных средств (состояние спроса полностью неопределенное). Прибыль должна гарантироваться при любом состоянии спроса. Определить оптимальную пропорцию транспортных средств (состояние спроса полностью неопределенное). Прибыль должна гарантироваться при любом состоянии спроса.
Решение
Определим верхнюю и нижнюю цену игры.
 А= А=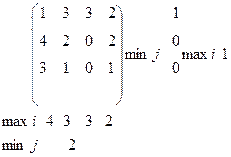
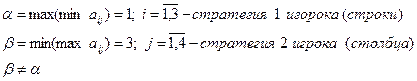
Игра не имеет Седловой очки, а значит ни один из участников н может использовать один план в качестве своей оптимальной стратегии, игроки переходят на «смешанные стратеги». Составим двойную пару задач линейного программирования. Для 1 игрока (предложения):
 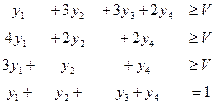
Освобождаясь от переменной V (цена игры), разделим уравнения системы на V. Приняв у/V за новую переменную Z, получим новую систему ограничений и целевую функцию.
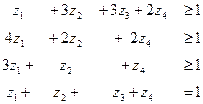
Z=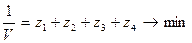
Аналогично для второго игрока (спрос)
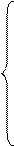 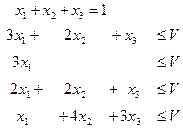
Приведем данные уравнения к форме без переменной V:
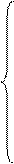 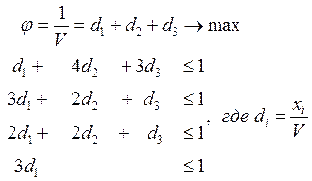 (*) (*)
Нам необходимо определить стратегию первого игрока (т.е. предприятия), т.е. относительную частоту использования его стратегий (х1
,х2
,…,хm
) будем определять, используя модель второго игрока, так как эти переменные находятся в его модели выигрыша. Приведем (*) к канонической форме:
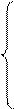 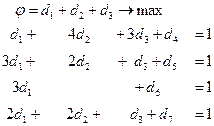
Решаем задачу симплексным методом.
итерация
0
|
базис |
d1
|
d2
|
d3
|
d4
|
d5
|
d6
|
d7
|
bi
|
bi
/ a |
| d4
|
1 |
4 |
3 |
1 |
0 |
0 |
0 |
1 |
1/3 |
| d5
|
3 |
2 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
| d6
|
3 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
| d7
|
2 |
2 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
| ψ |
-1 |
-1 |
-1 |
0 |
0 |
0 |
0 |
0 |
| 1 |
d3
|
1/3 |
4/3 |
1 |
1/3 |
0 |
0 |
0 |
1/3 |
1 |
| d5
|
8/3 |
2/3 |
0 |
-1/3 |
1 |
0 |
0 |
2/3 |
1/4 |
| d6
|
3 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1/3 |
| d7
|
5/3 |
2/3 |
0 |
-1/3 |
0 |
0 |
1 |
2/3 |
2/5 |
| Ψ |
-2/3 |
1/3 |
0 |
1/3 |
0 |
0 |
0 |
1/3 |
| 2 |
d3
|
0 |
1,25 |
1 |
0,375 |
-0,125 |
0 |
0 |
0,25 |
| d1
|
1 |
0,25 |
0 |
-0,125 |
0,375 |
0 |
0 |
0,25 |
| d6
|
0 |
-0,75 |
0 |
0,375 |
-1,125 |
1 |
0 |
0,25 |
| d7
|
0 |
0,25 |
0 |
-0,125 |
-0,625 |
0 |
1 |
0,25 |
| Ψ |
0 |
0,5 |
0 |
0,25 |
0,25 |
0 |
0 |
0,5 |
Базисное решение Б1
(0,25; 0; 0,25; 0; 0; 0,25; 0,25). Цена игры 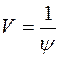 , так как , так как 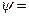 0,25+0,25+0=0,5 то V=2. 0,25+0,25+0=0,5 то V=2.
Исходные параметры относительно частот применения стратегий: х1
=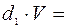 0,5; х2
=0; х3
=0,5; х4
=0; х5
=0; х6
=0,5; х7
=0,5. 0,5; х2
=0; х3
=0,5; х4
=0; х5
=0; х6
=0,5; х7
=0,5.
Задача 7
На двух предприятиях отрасли необходимо изготовить 300 изделий некоторой продукции. Затраты, связанные с производством изделий х на I предприятии, равны 4x1
2
руб., а затраты, обусловленные изготовлением х2
изделий на II предприятии, составляют 48х2
+ 8х2
2
(руб.).
Определить, сколько изделий на каждом из предприятий следует произвести, чтобы общие затраты, обусловленных изготовлением необходимой продукции, были минимальными.
Решение
f=4x1
2
+48х2
+ 8х2
2
→min
х1
+х2
=300
Составим функцию Лагранжа: F=f+λg
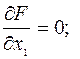 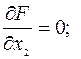
 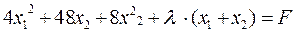
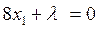
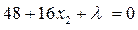
х1
+х2
=300
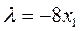 ; х2
=300-х1 ; х2
=300-х1
16(300-х1
)-8х1
+48=0
Тогда 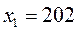 (деталей) (деталей)
х2
=300-202=88 (деталей)
Ответ: на первом предприятии следует произвести 202 детали, а на втором – 88 деталей.
Задача 9
Интервал планирования Т=5 лет. Функция затрат на ремонт а дальнейшую эксплуатацию К(τ)= 0,2τ+τ2
(р.). Функция замены Р(τ)=10+0,05τ2
(р.). Определить оптимальные планируемые затраты по годам пятилетки, если количество оборудования по возрастным группам n(τ=0)=10; n(τ=1)=12; n(τ=2)=8; n(τ=3)=5.
Решение
Рассчитаем переходы (затраты на замену и ремонт) оборудования для каждого из возможных состояний τ.
| τ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| К |
- |
1,2 |
4,4 |
9,6 |
16,8 |
26 |
37,2 |
50,4 |
65,6 |
| Р |
10 |
10,05 |
10,2 |
10,45 |
10,8 |
11,25 |
11,8 |
12,45 |
- |
Произведем пошаговую оценку альтернативных вариантов затрат для возможных различных состояний τ на каждом шаге t, т.е.
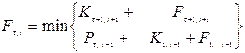
Начало оценивается с последнего t=5 шага.
Шаг 1; t=5.
Все состояния на последнем интервале приравниваются к 0:
F85
=0; F75
=0; F65
=0; F55
=0; F45
=0; F35
=0; F25
=0; F15
=0.
Шаг 2; t=4.
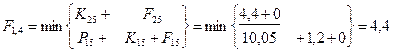
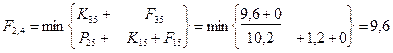
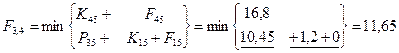
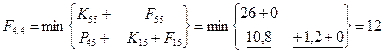
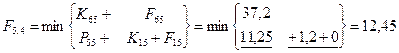
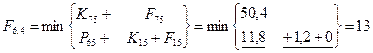
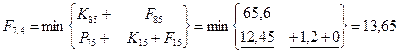
Шаг 3; t=3.
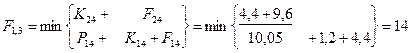
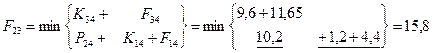
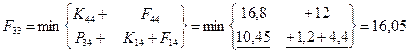
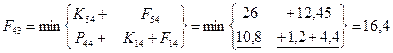
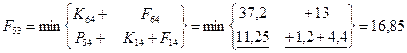
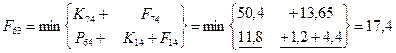
Шаг 4; t=2.
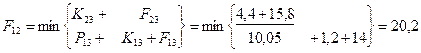
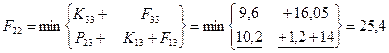
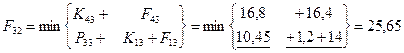
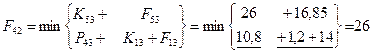
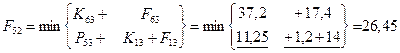
Шаг 5; t=1.
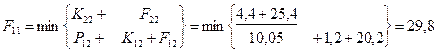
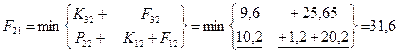
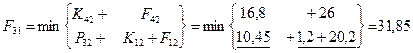
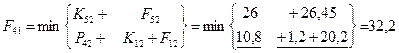
Шаг 6; t=0.
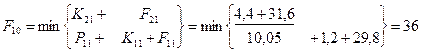
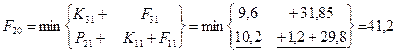
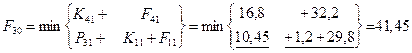
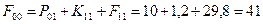
Функции затрат F00
, F10
, F20
, F30
– затраты на единицу оборудования соответственно для возраста τ=0,1,2,3 года. Определим стратегию замены и ремонта оборудования каждого возраста. На схеме стратегии выделены стрелками (только оптимальные шаги). Определяем затраты по годам планирования:
t=1; Q1
= 10*11,2+12*4,4+8*11,4+5*11,65=314,25
t=2; Q2
= (10+8+5)*4,4+12*11,4=238
t=3; Q3
= (10+8+5)*11,4+12*4,4=315
t=4; Q4
= (10+8+5)*4,4+12*11,4=238
t=5; Q5
=(10+8+5)* 9,6+12*4,4=237,6
Проверка: сумма затрат для оборудования каждого возраста должна равняться сумме затрат на них по годам планирования. Затраты на каждый возраст:

=41*10+36*12+41,2*8+41,45*5=1378,85
Сумма затрат по годам:
Q1
+ Q2
+ Q3
+ Q3
=314,25+238+315+238+237,6=1375,85

Задача 11
Дана схема движения транспорта с n=5 пунктами и расстояниями между ними. Построить кольцевой маршрут объезда всех пунктов наименьшей длины.
| ∞ |
13 |
12 |
11 |
7 |
| 10 |
∞ |
6 |
9 |
4 |
| 13 |
10 |
∞ |
12 |
7 |
| 9 |
6 |
14 |
∞ |
8 |
| 12 |
13 |
9 |
10 |
∞ |
Решение
Стоим приведенную матрицу с целью получения в каждой строке и столбце не меньше 1 кратчайшего маршрута (0 приведенного значения). Коэффициенты приведения
по строкам: К1
=7+4+7+6+9=33
| ∞ |
6 |
5 |
4 |
0 |
| 6 |
∞ |
2 |
5 |
0 |
| 6 |
3 |
∞ |
5 |
0 |
| 3 |
0 |
8 |
∞ |
2 |
| 3 |
4 |
0 |
1 |
∞ |
по столбцам (у приведенной матрицы): К2
=3+1=4
 Кпр
=33+4=37 (сумма самых коротких маршрутов). Кпр
=33+4=37 (сумма самых коротких маршрутов).
 ∞ ∞ |
6 |
5 |
3 |
0 |
| 3 |
∞ |
2 |
4 |
0 |
| 3 |
3 |
∞ |
4 |
0 |
| 0 |
0 |
8 |
∞ |
2 |
| 0 |
4 |
0 |
0 |
∞ |
Для нулевых значений определяем коэффициенты значимости:
К41
=0; К51
=0; К42
=3; К53
=2; К25
=2; К15
= К35
=3; К54
=3.
Выбираем аij
=0 с максимальным Кij
, например, К15
=3.
В матрице назначения присваиваем Х15
=1. В полученную матрицу в клетку (5,1) вводим запрет.
 Приведем матрицу. Приведем матрицу.
| 2 |
3 |
4 |
1 |
 2 2 |
∞ |
0 |
2 |
1 |
| 3 |
0 |
∞ |
1 |
0 |
| 4 |
0 |
8 |
∞ |
0 |
| 5 |
4 |
0 |
0 |
∞ |
Подсчитаем новое значение Кпр
: 37+2+3=42.
Определяем коэффициенты значимости для нулевых значений.
К32
=К42
= К53
=К41
=К31
=0; К23
= К54
=1.
Выбираем аij
=0 с максимальным Кij
, например, К23
=1.
В матрице назначения присваиваем Х23
=1. В полученную матрицу в клетку (3,2) вводим запрет.
| 2 |
 4 4 |
1 |
| 3 |
∞
|
1 |
0 |
| 4 |
0 |
∞ |
0 |
 5 5 |
4 |
0 |
∞ |
Так как матрица уже приведена, определяем коэффициенты значимости для нулевых значений.
К42
=4; К41
=0; К31
=1; К54
=5.
Присваиваем в матрице назначения Х54
=1. В полученную матрицу в клетку (4,1) вводим запрет.
В полученной матрице осталось два маршрута, которые и вносим в кольцевой маршрут: Х31
=1; Х42
=1.
Введем все маршруты в матрицу назначения.
Длина полученного маршрута:
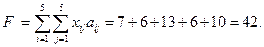
Условие оптимальности F=Кпр.
=42 выполняется, то полученный кольцевой маршрут является оптимальным.
Задача 13
Рассматривается круглосуточная работа пункта проведения профилактического осмотра автомашин. Пункт состоит из n=3 каналов; на осмотр каждой машины затрачивается 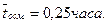 При осмотре группа выявляет дефект с вероятностью р=0,7; на осмотр поступает в среднем При осмотре группа выявляет дефект с вероятностью р=0,7; на осмотр поступает в среднем 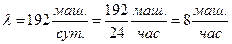 . Обслуживание одной заявки приносит среднюю прибыль С1
=3 руб./час, создание 1 канала требует среднего расхода С2
=18000 тыс.р., эксплуатация 1 канал в единицу времени требует среднего расхода С3
=8 руб./час. Определить характеристики работы пункта. Установить, при каких соотношениях С1
,С2
, С3
система будет рентабельна, и если система не рентабельна при заданных С1
,С2
, С3
, то при каких она будет рентабельна? Через какое время эксплуатации система будет приносить прибыль? . Обслуживание одной заявки приносит среднюю прибыль С1
=3 руб./час, создание 1 канала требует среднего расхода С2
=18000 тыс.р., эксплуатация 1 канал в единицу времени требует среднего расхода С3
=8 руб./час. Определить характеристики работы пункта. Установить, при каких соотношениях С1
,С2
, С3
система будет рентабельна, и если система не рентабельна при заданных С1
,С2
, С3
, то при каких она будет рентабельна? Через какое время эксплуатации система будет приносить прибыль?
Решение
Характеристики работы системы:
1. Среднее число занятых каналов
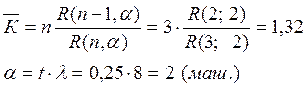
2. Вероятность выявления скрытого дефекта
Рабс.
=(1-Р0
)Р=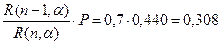
3. Абсолютная пропускная способность, считая все осмотренные машины:
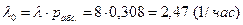
4. Полная абсолютная пропускная способность, считая все осмотренные машины:
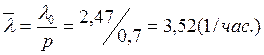
5. Вероятность того, что канал занят:
Пз.к.
=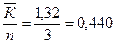
6. Среднее время простоя канала:
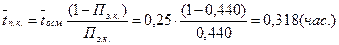
7. Вероятность того, что все группы будут заняты осмотром
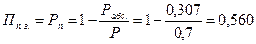
8. Среднее время неполной занятости системы (простоя хотя бы одной группы) (простоя хотя бы одной группы)
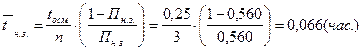
9. Средняя прибыль за сутки (t=24 часа)
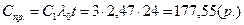
10 Средняя стоимость в сутки:
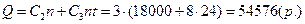
11. Прибыль, которую система начнет приносить через время, определяется условием: 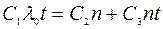
Условие рентабельности: 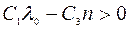
У нас 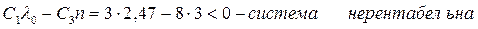 . .
Преобразуем это выражение с учетом того, что  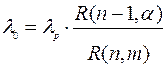 ; получим условие оптимальности: ; получим условие оптимальности: 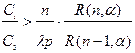
Система будет рентабельна, если: 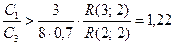
Из 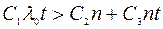 найдем время, через которое система начинает приносить прибыль: найдем время, через которое система начинает приносить прибыль:
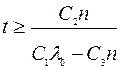 (дней) или (дней) или 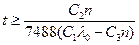 (лет) (лет)
Список используемой литературы
1. Данко П.Е. и др. Высшая математика в примерах и задачах. Ч2: Учебник для втузов. – М.: Высшая школа, 1986. – 415 с.
2. Конюховский П.В. Математические методы исследования операций в экономике. – СПб.: Питер, 2002. – 208 с.
3. Мельник М.М. Экономико-математические методы и модели в планировании МТС. – М.: Высшая школа, 1990. – 352 с.
Министерство образования Российской Федерации
«Тихоокеанский государственный университет»
КОНТРОЛЬНАЯ РАБОТА
ПО МЕТОДАМ И МАДЕЛЯМ В ЭКОНОМИКЕ
Выполнил: студент 3-го курса з/о
Специальность:________________
№ зач. книжки_________________
Ф.И.О._______________________
2010г.
|