1.
ЧР
наз. сходящимся
, если 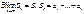
КК
сходимости ЧР:
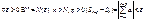
// Если ряд сходится, то

|
3. Интегральный ПК сх.Р:
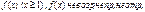
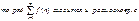
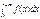
|
5. Признак Коши:
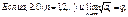
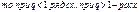
|
7. Признаки Абеля и Дирихле для ЧР:
Признак Абеля:
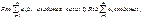
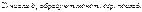
Признак Дирихле:
Ряд an
bn
сходится, если:
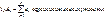
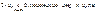
|
9. Действия над рядами.
По определению полагают:
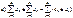
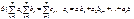
Равенство а) имеет неформальный смысл, если оба ряюа сходятся, а равенство б) – если, сверх того, по меньшей мере один из этих рядов сходится абсолютно.
|
11. КК РС функ. ряда:
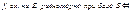
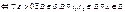
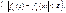
|
13. Признаки РС ф. рядов.
Признак Абеля: Ряд

сходится равномерно на X
, если: 1) Ряд an
сх. равн. на X
; 2) функции bn
(
x
)
ограничены в совокупности и "x
образуют монотонную последовательность.
Признак Дирихле:
Ряд (1) сходится равномерно на множествеX
, если: 1) Част. суммы an
(
x
) (
n
=1,…,
N
)
в совокупности ограничены; 2) посл-ть bn
(
x
) (
n
=1,2,…)
монотонна "x
и равномерно на X
стремится к нулю при n
®
µ
.
|
15. Непрерывность и
lim
пер.
Th
:
{ft
; t
ÎT
}, ft
: X
®
C
; B
-
база в T
. Если ft
сх.равн. к f
на X
при базе B
и функции ft
непрерывны в точке x
0
ÎX
,
то функция f
:X
®
C
тоже непрерывна в этой точке.
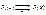
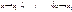
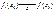
Следствие 1
: Если посл-ть функций, непрерывных на множестве, сходится на нем равномерно, то предельная функция тоже непрерывна на этом множестве.
Следствие 2
: Если ряд из функций, непрерывных на некотором множестве, сходится на нем равномерно, то сумма ряда тоже непрерывна на этом множестве.
|
17. Интегрирование и
lim
.
Th
:
{ft
, t
ÎT
}, ft
:[a
,b
]®C
; B
-
база T
; Если функции семейства интегрируемы на [a
,b
] и ft
сх. равн. к f
на [a
,b
] при базе B
, то предельная функция f
:[a
,b
]®C
тоже интегрируема на отрезке [a
,b
] и
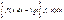
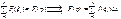

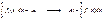
Следствие
: Если ряд из интегрируемых на [a
,b
] ф. сх.равн., то его сумма тоже интегрируема на [a
,b
],
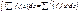
|
19. Характер сх. ст. ряда.
Th
:
Степенной ряд
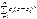
сходится в круге K
=
{z
ÎC
| | z – z0
| < R
}, радиус которого определяется по ф-ле Коши-Адамара:
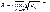
Вне этого круга ряд расходится. На любом замкнутом круге, лежащем строго внутри круга K
сходимости ряда, степенной ряд сходится абсолютно и равномерно.
|
21. Дифф. и
ò
ст. рядов:
Th
:
Если круг K
ÎC
сходимости ст. ряда
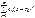
не сводится к единственной точке z
=
z
0
, то внутри K
сумма f
(
z
)
этого ряда дифференцируема, причем
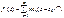
Кроме того, f
(
z
)
:K
®C
можно интегрировать по любому гладкому пути g:[0,1]®K
, и если
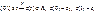
то
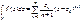
|
23. Ряд Тейлора.
Аналитическая в точке a
ф-я f
(x
) в некоторой окрестности этой точки разлагается в степенной ряд

Остаточный член
в форме Лагранжа
:
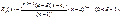
в форме Коши
:
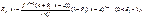
Основные разложения:
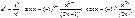
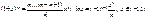
|
25. Алгебры функций.
Совокупность A
вещественно (комплексно)-значных функций на множестве X
наз. вещественной
(комплексной
) алгеброй функций
на X
, если из f
,g
ÎA
и a
ÎR
(
C
)
следует, что
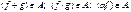
|
27. Теорема Стоуна:
Пусть A
– алгебра определенных на компакте K
непрерывных вещественнозначных функций. Если A
разделяет точки компакта K
и не исчезает на K
, то A
является всюду плотным подмножеством простанства C
(K
,R
).
|
29
. Теорема Вейерштрасса:
Если f
ÎC
([a
,
b
],C
), то $ {Pn
; n
ÎN
} многочленов Pn
:[a
,
b
]®C
, что Pn
сх. равн. к f
на [a
,
b
]. При этом, если f
ÎC
([a
,
b
],R
), то и многочлены Pn
можно выбрать из C
([a
.
b
],R
).
|
31. Дифф. и непр. собств.
ò
(пар)
.
Непрерывность
: P
=
{(x
,
y
)ÎR
2
| x
Î[a
,
b
], y
Î[c
,
d
]}. Если функция f
:P
®R
непрерывна, то ф-я
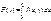
непрерывна в любой точке y
Î[c
,
d
].
Дифференцирование
: Если на прямоугольнике P
функция f
непрерывна и имеет непрерывную частную производную по y
, то интеграл принадлежит к классу C
(1)
([c
,
d
], R
), причем
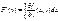
|
33. Пр. Вейерш.РС несоб.
ò
(
пар
).
Пусть f
(
x
,
y
),
g
(
x
,
y
)
интегрируемы по x
на любом отрезке [a
,
b
]Ì[a
,
w
] "y
ÎY
.
Если "x
Î[a
,
w
],
"y
ÎY
| f
(
x
,
y
)
| ≤ g
(
x
,
y
)
, а интеграл
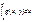
сходится равномерно на Y
, то интеграл
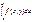
сходится абсолютно "y
и равномерно на мн-ве Y
.
|
35.
lim
перех. под. знаком.н.
ò
.
Th
:
Пустьf
(
x
,
y
)
– сем-во ф., интегрируемых хотя бы в несоб.смысле на x
Î[a
,
w
), и пусть BY
-база в Y
.
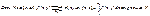 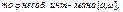
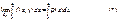
Следствие
: Пусть "y
ÎY
ÌR
вещ. ф-я f
(
x
,
y
)
неотрицательна и непрерывна на x
Î[a
,
w
). Если с ростом y
ф-ции f
(
x
,
y
)
, монотонно возрастая, стр. к j
(x
), jÎC
([a
,
w
],R
) и
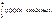
то справедливо равенство (*).
|
37. Дифф. н.
ò
(пар).
Th
:
Если
а)
ф-ции f
(
x
,
y
)
, f
’
y
(
x
,
y
)
непрерывны на {(x,y)ÎR
2
| x
Î[a
,
w
),y
Î[c
,
d
]},
b)
интеграл
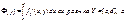
c)
интеграл
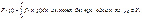
то он сх. равн. на Y
; при этом ф-я F
(
y
)
оказывается дифференцируемой и
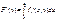
|
39. Интегрирование н.
ò
(пар):
Если f
(
x
,
y
)
непрерывна на {(x
,
y
)ÎR
2
| x
Î[a
,
w
),y
Î[c
,
d
]} и интеграл
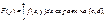
то ф-я F
интегрируема на [c
,
d
] и
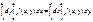
|
| 41.
|
43. Ряды Фурье.
Если X
–
Л.П. со скал. пр-ем < , >, а {lk
}–ортог. система ненулевых векторов в X
, то любому в. x
можно сопоставить ряд Фурье
:
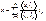
Экстремальное свойство
: "y
ÎL
||x
–
xl
||≤||x
–
y
||. Равенство возможно только при y
=xl
.
Неравенство Бесселя
:
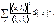
Равенство Парсеваля
:
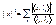
|
45. Гильбертово пр-во.
Линейное нормированное пр-во наз. гильбертовым
, если оно полно и имеет бесконечную размерность.
|
47. Тригонометр. ряд Фурье.
Систему экспонент
{einx
;n
ÎN
} называют триг. сист. в комплексной записи.
Она явл. ортогон. с. в-в пр-ва R
([-p
,p
], C
) отн. скал. пр-ния в-в.
Сопоставляемый ф. f
триг.ряд
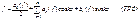
наз. триг.рядом Фурье ф-ции
f
.
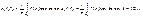
Th
:
(ТРФ
)"f
ÎR
([-p
,p
],C
)сх.к f
в средн.,т.е.f
=ТРФ,
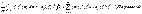

|
49. Лемма Римана.
Если локально интегрируемая ф-я f
:[w
1
,w
2
]®R
абсолютно интегрируема (хотя бы в несоб смысле), на промежутке [w
1
,w
2
], то

|
51. Д.У.сх.ряда Фурье в т.
Гов., что f
:U
0
®
C
, заданная в проколотой окр-ти точки x
ÎR
, удовлетворяет усл. Дини
, если
а) в т. x
$ оба односторонних предела
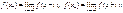
б) сходится абсолютно следующий интеграл:
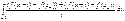
Th
:
f
:R
®C
– 2p-периодич.ф-я, абс.инт-я на [-p,p]. Если f
удовл. в т. x
ÎR
условиям Дини, то её ряд Фурье сходится в точке x
, причем
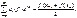
|
53.Свойства пр-ва
CL
2
[-∞,+
∞]
_____________
|
55. Преобразование Фурье.
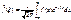
называется нормиров.преобр. Фурье
ф-ции f
:R
®
C
.
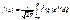
называется интегралом Фурье
ф-ции f
.
Свойства
: 1. Линейность преобразования Фурье.
2. Th
:
f
:R
®
C
– абс. инт-мая ф-я, кусочно непрерывная на каждом конечном отрезке числ. Оси R
. Если ф-я f
удовл. Усл. Дини в x
ÎR
, то её òФурье сх. в этой точке к значению ½(f
(x-
)+f
(x+
)).
|
57. Пр-е Фурье для ф. мн.пер.
f
:R
®C
– лок. инт. на Rn
ф-ция. Функция
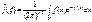
называется преобр. Фурье функции
f
.
Многомерное пр-е Фурье можно рассматривать как n
одномерных преобразований Фурье, проведенных по каждой из переменных x
1
,
…,
xn
.
|
59. Теорема обращения.
Оператор, определяемый равенством
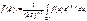
называется обратным преорбазованием Фурье
.
Формула обращения преобразования Фурье
:
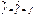
или в форме интеграла Фурье
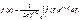
|
10. Сх. и РС семейства
f
(ПАР)
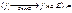
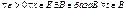
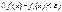
_________________________
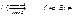
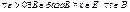 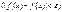
|
8. Теорема Римана:
Сумму условно сходящегося ряда путем перестановки слагаемых можно сделать равной любому числу.
|
6. Признак Лейбница:
Условно сходищимся
наз. ряд an
, если ряд an
сходится, а ряд |an
| -расходится.(n=1,2,…)
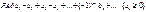
сходится (вообще гов. не абсолютно), если
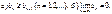
В этом случае для остатка ряда
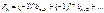
имеем оценку
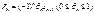
|
4. Признак Даламбера:

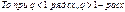
|
2. Признак сравнения
I
:
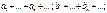
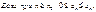
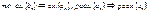 Признак сравнения
II
: Признак сравнения
II
:
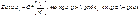
|
20. Теоремы Абеля.
Первая Теорема Абеля
: Если степенной ряд
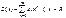
сх. в концевой точке x
=
R
интервала сход-ти, то
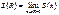
Вторая Теорема Абеля
: Если степенной ряд
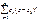
сходится в некоторой точке zÎС
, то он сходится равномерно на отрезке с концами z
0
,z
.
|
18.
Дифференцирование и
lim
.
Th
:
{ft
, t
ÎT
}–семейство ft
: X
®C
, определенных на выпуклом ограниченном мн-ве X
; B
-
база T
. Если функции семейства дифференцируемы на X
, семейство {ft
’
, t
ÎT
} производных сх. равн. на X
к некоторой ф-ции j
:X
®C
, а исходное семейство сх. хотя бы в одной точке x
0
ÎX
, то оно сх. равн. на всем мн-ве X
к дифференцируемой функции f
:X
®C
, причем f
’
=
j
.
|
16. Теорема Дини:
Если последовательность непрерывных на компакте функций сходится на нем монотонно и к непрерывной же функции, то эта сходимость равномерная.
Следствие
: Если члены ряда an
(x
) (n
=1,2,…) суть неотрицательные непрерывные на компакте K
функции an
: K
®
R
и ряд сходится на K
к непрерывной функции. То он сходится на K
равномерно.
|
14. Условия комм. 2х пр.пер:
Th
:
{Ft
;t
ÎT
}, Ft
: X
®
C
; BX
–
база в X
,BT
–
база в T
. Если при базе BT
cем-во сх. равн. на X
к F
:X
®
C
, а "t
$
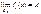
то $ оба повторных предела
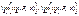
и имеет место равенство этих пределов
.
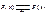

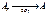
|
12. Признак Вейерштрасса РС функционального ряда:
u
1
(
x
)+…+
un
(
x
)+…
сходится абсолютно и равномерно на множестве X
, если существует сходящийся числовой ряд c
1
+
c
2
+…+
cn
+…
такой, что
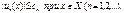
|
30. Собственные
ò
, их интег-е.
Интеграл, зависящий от параметра, – это ф-я вида

Если "t
ò явл. собственным, то F
есть собственный интеграл, зав. от параметра.
Th
:
Если ф-яf
:P
®R
непрерывна в прямоугольнике P
=
{(x
,
y
)ÎR
2
| x
Î[a
,
b
], y
Î[c
,
d
]}, то интеграл

интегрируем на отрезке [c
,
d
] и имеет место рав-во
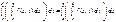
|
28.
Компл. вар. теоремы Стоуна:
Если комплексная алгебра A
функций f
:X
®
C
не вырождается на X
и разделяет точки X
, то при условии самосопряженности алгебры A
можно утверждать, что она плотна в C
(X
,C
).
|
26. Банахова Алгебра в С
(
K
).
Нормированная алгебра называется Банаховой
, если она является нормированным линейным пространством, полным относительно метрики, порожденной нормой (B
-пространством).
Подмн-во пространства C
(
K
,
Y
) наз. всюду плотным
, если функциями, составляющими это мн-во, можно со сколь угодно малой абсолютной погрешностью аппроксимировать любую непрерывную функцию f
:K
®Y
.
|
24. Формула Стирлинга.
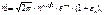
где

Или
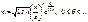
|
22. Аналит. ф. в действ. обл.
|
40. Эйлеровы интегралы.
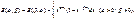
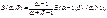
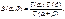
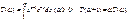
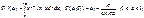
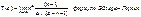
|
38. Интеграл Дирихле.
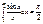
|
36. Непрерывность н.
ò
(пар):
Если а)
ф-я f
(
x
,
y
)
непрерывна на {(x,y)ÎR
2
| x
Î[a
,
w
),y
Î[c
,
d
]}, b
)
интеграл
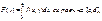
то ф-я F
(
y
)
непрерывна на [c
,
d
].
|
34. Пр. Абеля-Дирихле РС.н.
ò
.
Th
:
Пусть f
(
x
,
y
),
g
(
x
,
y
)
"y
ÎY
интегрируемы по x
на любом отрезке [a
,b
]Ì[a
,
w
]. Для равн.сх. интеграла
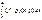
на мн-ве Y
достаточно:
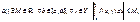
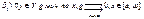
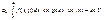
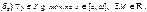 
|
32. Несоб.
ò
(пар)
, КК РС.
Говорят, что несобственный интеграл
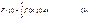
зав. от пар. y
ÎY
, сх. равн. на мн-ве E
ÌY
, если
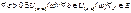
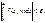
КК
: Чтобы несоб. ò (1) сходился равномерно на множестве E
ÌY
Û
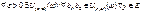
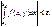
|
50. Ядра Дирихле.
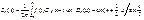
Dn
называется ядром Дирихле
. Ядро Дирихле 2p-периодично, четно, и, кроме того,
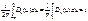
|
48. Ряды Фурье д/чет./неч. ф.
а)
Если ф-я f
(
x
)
четная, то

б)
если ф-я f
(
x
)
нечетная, то
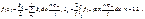
Ряд Фурье в комплексной форме
:
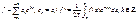
Th
(О сх-ти в среднем)
:
"f
(
x
)
ÎR
([-p
,p
],C
)
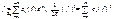
|
46. Предгильбертово пр-во.
Линейное нормированное пр-во бесконечной размерности наз. предгильбертовым
, если оно не полно по отношению к метрике, индуцированной естественной нормой в нем.
|
44. Ортонорм. сист.в-в.
Система в-в наз. {
ek
; k
ÎK
}ортонормированной
, если "i
,
j
ÎK
< ei
,ej
>=d
i
,
j
, где d
i
,
j
– символ Кронекера
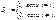
Система {x
a
; a
ÎA
} в-в нормир.пр-ваX
наз. полной по отношению к мн-ву
E
ÌX
, если "x
ÎE
можно сколь угодно точно в смысле нормы пр-ва X
приблизить конечными лин. комб-ми в-в системы.
В конечномерном пр-ве X
полнота в X
сист.в-в, как следует из сообр. компактности и непрер-ти, равносильна тому, что эта сист. явл. базисом в X
.
Th
:
X
– лин.пр-во со скал. пр-ем < , >; l
1
,…,
ln
,…
– кон. или счет.сист.¹0 вз. ортогон.в-в X
. Þ Эквив:
a
)
{lk
} полна по отн. к E
ÌX
;
b
)
"x
ÎE
ÌX
им.место
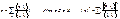
|
42. Интеграл Пуассона
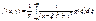
|
60. Теорема Планшереля.
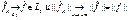
L
2
– пополнение (S
,
d
), d
– метрика сходимости в смысле среднего квадратичного уклонения на Rn
.
|
58. Пространство
S
(
Rn
).
S(Rn
,
C
) – сов-ть всех ф-ций f
ÎC(∞)
(Rn
,
C
), удовлетворяющих условию
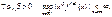
такие ф-ции наз. быстро убывающими
.
Если f
ÎS
, то
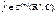
Более того,

|
56. Пр-е Фурье свертки.

- Ф-лы, связывающие операции свертки и умножения функций посредством пр.Фурье.
|
54. Теорема Фейера.
f
: R
®C
– 2p-периодическая абс. инт-мая на [-p,p] ф-я. Тогда
a) если на E
ÌR
f
равномерно непрерывна, то
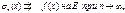
b) если f
ÎC
(R
,C
), то
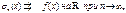
c) еслиf
непрерывна в x
ÎR
, то
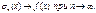
__________________________________________
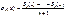
|
52. ДУ РС триг. ряда Фурье.
Th
:
Если f
:[-p,p]®C
такова, что а) f
ÎC
(
m
-1)
[-p,p], m
ÎN
; b) f
(
j
)
(-p)=
f
(
j
)
(p), j=0,1,…m
–
1; c) f
имеет на [-p,p] непрерывную производную f
(
m
)
порядка m
>=1,
то ряд Фурье ф-й f
сх. к f
абсолютно и равномерно на отрезке [-p,p], причем отклонение n
-
й частичной суммы Sn
(x
) ряда Фурье от f
(
x
)
на всем отрезке [-p,p] имеет оценку
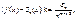
где {e
n
}–стремящаяся к нулю посл-ть положительных чисел.
|
|