Раздел 1.
Теория случайных чисел.
Все события делятся на детерминированные, случайные и неопределенные.
Если событие наступает в эксперименте всегда, оно называется достоверным
, если никогда – невозможным
. Это детерминированные события.
Статистическое определение вероятности:
Если в опыте, повторяющемся n раз, событие появляется mA
раз, тогда относительная частота наступления события: 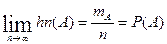 . Р(А) – вероятность наступления события А. . Р(А) – вероятность наступления события А.
Для достоверного
события W: Р(W)=1. Для невозможного
события Æ: Р(Æ)=0.
0 £ P(A) £ 1, т.к. 0£mA
£n - 0 £ hn(A) £ 1
W
mA
=n hn(A)=1
Æ
mA
=0 hn(A)=0
Все мыслимые взаимоисключающие исходы опыта называются элементарными событиями
. Наряду с ними можно наблюдать более сложные события – комбинации элементарных.
Несколько событий в данном опыте называются равновозможными
, если появление одного из них не более возможно, чем другого.
Классическое определение вероятности:
Если n-общее число элементарных событий и все они равновозможные, то вероятность события А:
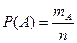 , ,
где mA
- число исходов, благоприятствующих появлению события А.
Раздел 2.
Сложные события.
Теория сложных событий позволяет по вероятностям простых событий определять вероятности сложных. Она базируется на теоремах сложения и умножения вероятностей.
1) Суммой (объединением)
двух событий А и В называется новое событие А+В, заключающееся в проявлении хотя бы одного из этих событий.
2) Произведением (пересечением)
двух событий А и В называется новое событие АВ, заключающееся в одновременном проявлении обоих событий. А*В=АВ, АА=А, АВА=АВ.
3) Событие А влечет за собой появление события В, если в результате наступления события А всякий раз наступает событие В. АÌВ
А=В: АÌВ, ВÌА
Два события называются несовместными
, если появление одного из них исключает возможность появления другого.
Если события несовместны, то АВ=Æ.
События А1
, А2
, …Аn
образуют полную группу событий в данном опыте, если они являются несовместными и одно из них обязательно происходит:
Ai
Aj
=
Æ
(i
¹
j, i,j=1,2…n)
A1
+A2
+…+An
=
W
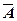 -
событие противоположное событию А, если оно состоит в не появлении события А. -
событие противоположное событию А, если оно состоит в не появлении события А.
А и 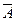 - полная группа событий, т.к. А+
- полная группа событий, т.к. А+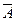 =W, А =W, А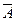 =Æ. =Æ.
Теорема сложения вероятностей.
Вероятность суммы несовместных событий
равна сумме вероятностей событий:
Р(А+В+С+…) = Р(А) + Р(В) + Р(С) +…
Следствие.
Если события A1
+A2
+…+An
- полная группа событий, то сумма их вероятностей равна 1.

P(A+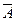 ) = P(A) + P(
) = P(A) + P(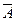 ) = 1 ) = 1
Вероятность наступления двух совместных событий
равна:
Р(А+В) = Р(А) + Р(В) - Р(АВ)
Р(А+В+С) = Р(А) + Р(В) + Р(С) – Р(АВ) – Р(АС) – Р(ВС) – Р(АВС)
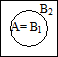
Теорема.
Если АÌВ, то Р(А) £ Р(В).
В=В1
+В2
(В1
=А) Р(В)=Р(В1
) + Р(В2
)= Р(А) + Р(В2
)
Теорема умножения вероятностей. Условные вероятности.
Опыт повторяется n раз, mB
раз наступает событие В, mАВ
раз наряду с событием В наступает событие А.
hn(B) = 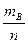 hn(AB) = hn(AB) =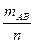
Рассмотрим относительную частоту наступления события А, когда событие В уже наступило:
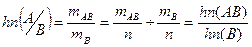
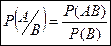 - условная вероятность события А по событию В
– вероятность события А, когда событие В уже наступило. - условная вероятность события А по событию В
– вероятность события А, когда событие В уже наступило.
Свойства условных вероятностей.
Свойства условных вероятностей аналогичны свойствам безусловных вероятностей.
1. 0 £ Р(А/В) £ 1, т.к. 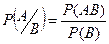 ; АВ Ì В, Р(АВ) £ Р(В) ; АВ Ì В, Р(АВ) £ Р(В)
2. Р(А/А)=1
3. ВÌА, - Р(А/В)=1
4. 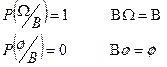
5. Р[(A+C)/B] = Р(А/В) + Р(C/В)
– Если события А и С несовместны
Р[(A+C)/B] = Р(А/В) + Р(C/В) - Р(АC/В)
– Если события А и С совместны
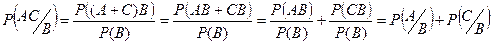
Теорема
. Вероятность произведения двух событий равна произведению вероятности одного события на условную вероятность другого.
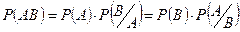
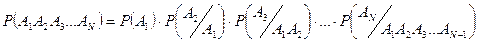
Свойства независимых событий.
Если события А и В независимы, то независимы и каждая из пар: А и В, А и 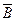 , , 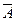 и В, и В, 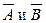 . .
Если события Н1
, Н2
, …Нn
независимы, то заменяя любые из них на противоположные, вновь получаем независимые события.
Формула полной вероятности.
Вероятность события В, которое может произойти совместно только с одним из событий Н1
, Н2
, …Нn
, образующих полную группу событий, вычисляется по формуле:

События А1
, А2
, …Аn
называют гипотезами
.
Теорема гипотез (формула Байеса).
Если до опыта вероятности гипотез были Р(Н1
), Р(Н2
)…Р(НN
), а в результате опыта произошло событие А, то условные вероятности гипотез находятся по формуле:
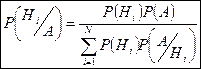
Пример.
На трех технологических линиях изготавливаются микросхемы. Найти: 1) вероятность того, что случайно выбранное изделие оказывается бракованным; 2) вероятность того, что если изделие дефектно, то оно изготовлено на 1 линии.
| № линии |
Количество изготавливаемых микросхем |
Вероятность брака |
| 1 |
25% |
5%; |
| 2 |
35% |
4% |
| 3 |
40% |
2% |
Рассмотрим события: Н1
, Н2
,…Нi
,…,НN
(полная группа событий)– изделие изготавливается i линией; А{изделие с браком}.
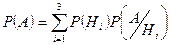
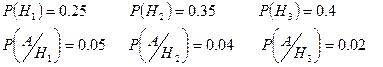
1) Р(А)=0,25*0,05+0,35*0,04+0,4*002=0,0345=3,45%
2) 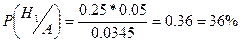
Схема последовательных испытаний Бернулли.
Проводится серия из n испытаний, в каждом из которых с вероятностью р может произойти событие А, с вероятностью q=1-р событие 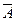 . .
Вероятность наступления события А не зависит от числа испытаний n и результатов других испытаний.
Такая схема испытаний с двумя исходами (событие А наступило либо не наступило) называется схемой последовательных испытаний Бернулли.
Пусть при n испытаниях событие А наступило k раз, (n-k) раз событие 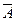 . .
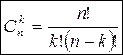 - число различных комбинаций события А - число различных комбинаций события А
Вероятность каждой отдельной комбинации: 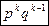
Вероятность того, что в серии из n испытаний событие А, вероятность которого равна р, появится k раз: 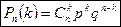
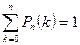 - условие нормировки. - условие нормировки.
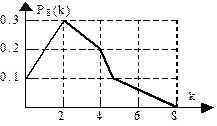 Пример.
Вероятность изготовления нестандартной детали равна р=0,25, q=0.75. Построить многоугольник распределения вероятностей числа нестандартных деталей среди 8 изготовленных. Пример.
Вероятность изготовления нестандартной детали равна р=0,25, q=0.75. Построить многоугольник распределения вероятностей числа нестандартных деталей среди 8 изготовленных.
N=8 p=0.25 q=0.75
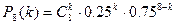
Если k0
– наивероятнейшее число,
то оно находится в пределах:
np-q £ k0
£ np+q
Если число (np+q) нецелое, то k0
– единственное
Если число (np+q) целое, то существует 2 числа k0
.
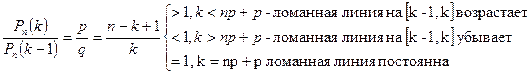
Предельные теоремы в схеме Бернулли.
1. Предельная теорема Пуассона
. При р»0, n-велико, np= l£ 10.
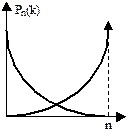 
Формула дает распределение Пуасона, описывает редкие события.
2. Предельная теорема Муавра-Лапласа.
0 £ p £ 1, n –велико, np>10
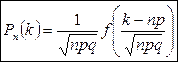
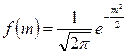 - стандартное нормальное распределение - стандартное нормальное распределение
3. Предельная интегральная теорема Муавра-Лапласа.
В условиях предыдущей теоремы вероятность того, что событие А в серии из n испытаний наступит не менее k1
раз и не более k2
раз:
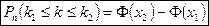
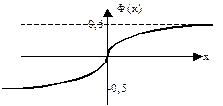 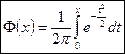 - функция Лапласа - функция Лапласа
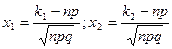
Следствие:
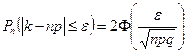
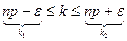
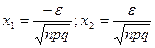
Пример.
ОТК проверяет на стандартность 1000 деталей. Выбранная деталь с вероятностью р=0,975 является стандартной.
1) Найти наивероятнейшее число стандартных деталей:
K0
=np=975
2) Найти вероятность того, что число стандартных деталей среди проверенных отличается от k0
не более чем на 10.
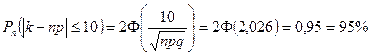
3) С вероятностью 0,95 найти максимальное отклонение числа стандартных деталей среди проверенных.
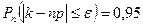
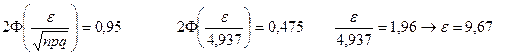
4) Найти число проверяемых деталей n, среди которых с вероятностью 0,9999 стандартные детали составят не менее 95%.
0,95n£k£n
P(0,95n£k£n)=0.9999 = Ф(х2
)- Ф(х1
) = 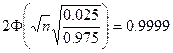
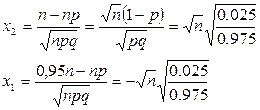
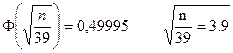 n=3.92
*39=594 n=3.92
*39=594
при р=0,9999 n=594
при р=0,999 n=428
при р=0,99 n=260
Раздел 3.
Случайные величины и распределение вероятностей.
Случайная
– величина, которая в ходе опыта принимает то или иное значение из возможных своих значений, меняющееся от опыта к опыту и зависящее от множества непредсказуемых факторов.
Если случайные события характеризуют процесс качественно, то случайная величина – количественно.
Случайная величина – численная функция, задаваемая на множестве элементарных событий. На одном множестве может быть несколько случайных величин.
Дискретная случайная величина (ДСК)
– величина, принимающая счетное (конечное или бесконечное) множество значений.
Непрерывная случайная величина (НСВ)
– случайная величина, значения которой образуют несчетные множества. (Например, расход бензина на 100 км у автомобиля Жигули в Нижнем Новгороде).
Задать св – значит указать все множество ее значений и соответствующие этим значениям вероятности. Говорят, что задан закон распределения случайной величины.
Случайная величина может быть задана несколькими способами:
1. Табличный.
| Х
|
a1
|
a2
|
… |
аn
|
| Р
|
p1
|
p2
|
… |
pn
|
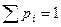
Значения случайных величин в таблице ранжируются, т.е. указываются в порядке возрастания.
Недостпаток табличного способа в том, что он пригоден только для случайных величин, принимающих небольшое количество значений.
2. Функция распределения
F
(
x
) =
P
(
X
<
x
)
или интегральный закон распределения.
Указывается вероятность того, что случайная величина принимает значение < x.
| Х
|
a1
|
a2
|
a3
|
… |
аn-1
|
| Р
|
p1
|
p2
|
p3
|
… |
pn-1
|
| F(x)
|
p1
|
p1
+
p2
|
p1
+
p2
+
p3
|
… |
p1
+
p2
+…+
pn-1
|
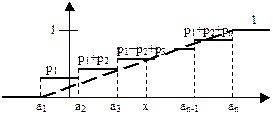
При увеличении значения случайной величины, количество ступенек функции F(х) возрастает, уменьшается их высота и в пределе при  получаем гладкую непрерывную функцию F(х). получаем гладкую непрерывную функцию F(х).
Свойства функции
F
(х).
1. Неотрицательна. 0£ F(х)£1
2. Неубывающая F(х2
)> F(х1
) при х2
>х1
3. 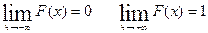
4. Р(
a
<
x
<
b
) =
F
(
a
) –
F
(
b
)
Вероятность того, что значение х попадет в интервал (а,b) определяется разностью значений функции на концах интервала.
Наряду с F(х) вводится f
(
x
) -
функция плотности вероятности или дифференциальный закон распределения:
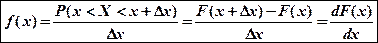
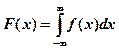
Свойства функции f(x):
1. Неотрицательна. (т.к. F(x) неубывающая, f
(
x
)
³
0
)
2.  Площадь фигуры под кривой на интервале (a,b) равна: Площадь фигуры под кривой на интервале (a,b) равна: 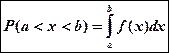
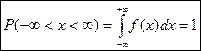 - условие нормировки функции f
(
x
). - условие нормировки функции f
(
x
).
Основные дискретные и непрерывные случайные величины.
Дискретные случайные величины (ДСВ).
1. Биноминальная случайная величина x{0,1,2,3…n}
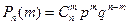 , p+q=1, 0<p<1 , p+q=1, 0<p<1
2. Пуассоновская случайная величина x{0,1,2,3…}

3. Бернуллиевая случайная величина 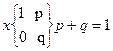
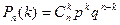
4. Равномерное распределение 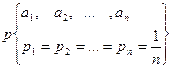
Непрерывные случайные величины (НСВ).
1.
Равномерное распределение
 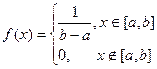
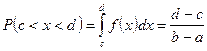
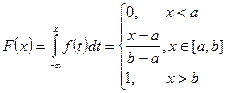
2.
Треугольное распределение Симпсона
 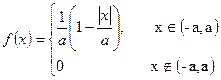
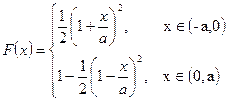
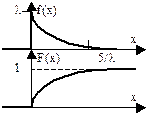 3.
Экспоненциальное (показательное) распределение. Имеет важное значение в теории массового обслуживания и теории надежности. 3.
Экспоненциальное (показательное) распределение. Имеет важное значение в теории массового обслуживания и теории надежности.
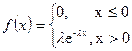
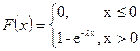
l - интенсивность.
3.
Нормальный закон распределения.
 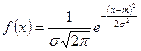 , s>0 , s>0
s=1, m=0 – нормальное стандартное распределение (m-мат. ожидание)
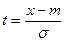 - такой подстановкой любое нормальное распределение приводится к стандартному. - такой подстановкой любое нормальное распределение приводится к стандартному.
При фиксированном s и изменяющемся m, кривая двигается вдоль Ох, не изменяя формы.
При фиксированном m и изменяющемся s (s1
<s2
<s3
), кривая вытягивается вдоль оси ординат, но площадь фигуры под каждой кривой = 1.
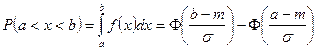
Функция Лапласа: 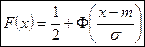
Операции со случайными величинами
Со случайными величинами, рассмотренными на одном и том же интервале исходов опыта, можно обращаться как с обычными числами и функциями.
X:
| X
|
a1
|
a2
|
… |
an
|
| p
|
p1
|
p2
|
… |
pn
|
Y=j(x)
Нужно найти закон распределения СВ Y. yk
=j(ak
), где k=1,2,…,n.
P(y=yk
)=P(x=ak
)=Pk
Если все значения СВ Y различны, то их надо проранжировать и указать соответствующие вероятности.
Если СВ Y принимает совпадающие значения, то их надо объединить под общей вероятностью, равной сумме соответствующих вероятностей, а после в ранжированном виде привести в таблице.
X={0,1,2,…,9}, P(x=k)=0.1, k=0,1,…,9, Y=x2
, Z=(x-5)2
.
| X
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| P
|
0.1 |
0.1 |
0.1 |
0.1 |
0.1 |
0.1 |
0.1 |
0.1 |
0.1 |
0.1 |
| Y
|
0 |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
| Py
|
0.1 |
0.1 |
0.1 |
0.1 |
0.1 |
0.1 |
0.1 |
0.1 |
0.1 |
0.1 |
| Z |
25 |
16 |
9 |
4 |
1 |
0 |
1 |
4 |
9 |
16 |
| Pz
|
0.1 |
0.1 |
0.1 |
0.1 |
0.1 |
0.1 |
0.1 |
0.1 |
0.1 |
0.1 |
Закон распределения СВ Z:
| Z
|
0 |
1 |
4 |
9 |
16 |
25 |
| Pz
|
0.1 |
0.2 |
0.2 |
0.2 |
0.2 |
0.1 |
Бинарные операции (с несколькими величинами)
СВ X,Y заданы в 1 опыте.
| Исход опыта |
E1
|
E2
|
… |
En
|
| Вероятность исхода
|
P1
|
P2
|
… |
Pn
|
| X
|
X1
|
X2
|
… |
Xn
|
| Y
|
Y1
|
Y2
|
… |
Yn
|
| Z=
j
(XY)
|
Z1
|
Z2
|
… |
Zn
|
Сложнее, если СВ задана только своим распределением:
| X
|
a1
|
a2
|
… |
an
|
| Р
|
p1
|
p2
|
… |
pn
|
| Y
|
b1
|
b2
|
… |
bn
|
| Р
|
g1
|
g2
|
… |
Gn
|
Z=X+Y
СВ Z принимаетзначения ak
+bs
, где ak
=a1
,a2
,…,an
; bs
=b1
,b2
,…bm
.
Общее количество возможных значений СВ = m×n.
P(Z=ak
+bs
)=P(X=ak
, Y=bs
)
Для нахождения такой вероятности необходимо знать закон совместного распределения СВ X и Y.
Набор точек (ak
,bs
) вместе с вероятностями P(X=ak
, Y=bs
) называется совместным распределением СВ
X
и
Y
. Обычно такое распределение задается таблицей.
Определение закона распределения суммы СВ по законам распределения слагаемых называется композицией законов распределения
.
X \Y
|
b1
|
b12
|
… |
bs
|
… |
bm
|
Px
|
| a1
|
P11
|
P12
|
… |
P1s
|
… |
P1m
|
P1
|
| a2
|
P21
|
P22
|
… |
P2s
|
… |
P2m
|
P2
|
| … |
… |
… |
… |
… |
… |
… |
… |
| ak
|
Pk1
|
… |
… |
Pks
|
… |
Pkm
|
Pk
|
| … |
… |
… |
… |
… |
… |
… |
… |
| an
|
Pn1
|
Pn2
|
… |
Pns
|
… |
Pnm
|
Pn
|
| Py
|
g1
|
g2
|
… |
gs
|
… |
gm
|
1 |
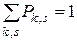
Наиболее просто вероятности Pks
находятся в случае независимости СВ X и Y. Две СВ X и Y называются независимыми
тогда и только тогда, когда
P(X=ak
, Y=bs
)=P(X=ak
)×P(Y=bs
)
Pks
=Pk
×Ps
По известному закону распределения совместного распределения СВ X и Y могут быть найдены одномерные законы распределения СВ X и Y.
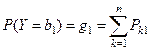 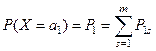
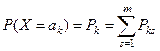
Теорема
. Если СВ Х,Y являются независимыми, то любые функции j(Х) и y(У) от этих величин также являются независимыми.
Распределение функции от случайной величины
Х – непрерывная СВ 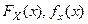
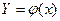 . По закону распределения СВ Х. Найти закон распределения СВ Y. . По закону распределения СВ Х. Найти закон распределения СВ Y.
Если СВ ХÎ[х0
,х1
], то 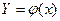 Î [y0
,y1
]. Î [y0
,y1
].
Предполагается, что функция j(х) является однозначной и имеет обратную функцию q(y).
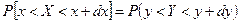
Воспользовавшись элементами вероятности:
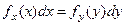 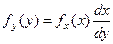
получим 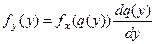 . .
Закон распределения не меняется, если q(y) является линейной.
fy
(y)=fx
(x).
Многомерные законы распределения СВ
Часто при решении практических задач мы имеем дело не с одной, а с совокупностью нескольких случайных величин, которые взаимосвязаны
.
nx1
,x2
,…,xn
n
-мерная случайная величина
– совокупность n взаимосвязанных случайных величин. Для ее описания используются многомерные законы распределения.
Двумерные функции распределения
X,YF(x,y)=P(X<x,Y<Y)
Функция F
(
x
,
y
)
обладает свойствами, аналогичными свойствам одномерной функции:
– не убывающая 1. x2
³x1
ÞF(x2
,y)³F(x1
,y)
– не отрицательная y2
³y1
ÞF(x,y2
)³F(x,y1
)
0£F(x,y)£ 1 2. F(¥,¥)= 1 F(-¥,-¥)=0
3. Fx
(x)=P(X<x+=P(X<x,Y<¥)=F(x,¥)
Fy
(y)=P(Y<y)=P(X<¥,Y<y)=F(¥,y)
f
(
x
,
y
) –
функция плотности вероятности совместного распределения величин x
и y
.
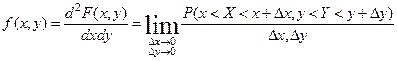
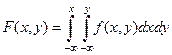
1. f(x,y)³0
2.
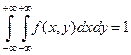 – условие нормировки – условие нормировки
3. По известным двумерным находятся соответствующие одномерные
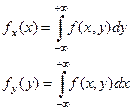 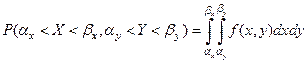
В случае статистической независимости СВ Х и У
F(x,y)=Fx
(x)×Fy
(y)
f(x,y)=fx
(x)×fy
(y)
F(x,y)=Fx
(x)×Fy
(y/x)=Fx
(x/y) – для условных
f(x,y)=fx
(x) ×f(y/x)=fy
(y) ×f(x/y)
Раздел 4. Числовые характеристики СВ
Исчерпывающие представления о СВ дает закон её распределения.
Во многих задачах, особенно на заключительной стадии, возникает необходимость получить о величине некоторое суммарное представление: центры группирования СВ – среднее значение или математическое ожидание, разброс СВ относительно её центра группирования.
Эти числовые характеристики в сжатой форме отражают существенные особенности изучаемого распределения.
Математическое ожидание (МО)
М(х), МО(х), mx
, m
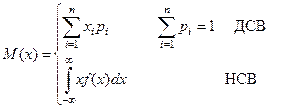
Основные свойства МО:
1. М(х) СВ Х Þ Хmin
£М(х)£Хmax
2. М(С)=С МО постоянной величины есть величина постоянная
3. М(Х±У)=М(Х) ±М(У)
4. М(Х×У)=М(х) ×М(у) Þ М(Сх)=СМ(х) – МО произведения двух независимых СВ
5. М(аХ+вУ)=аМ(Х)+вМ(У)
6. М(Х-m)=0 – МО СВ Х от её МО.
МО основных СВ
Дискретные Случайные Величины
1. Биноминальные СВ МО(Х)=np
2. Пуассоновские СВ МО(Х)=l
3. Бернуллиевы СВ МО(Х)=р
4. Равномерно распред. СВ 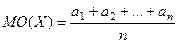
Непрерывные Случайные Величины
1. Равномерно распределенная СВ 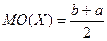
2. Нормально распределенная СВ MO(X)=m
3. Экспоненциально распределенная СВ 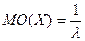
Дисперсия СВ
1. R=Xmax
-Xmin
– размах СВ
2. M(|X-m|) – среднее абсолютное отклонение СВ от центра группирования
3. M(X-m)2
– дисперсия – МО квадрата отклонения СВ от центра группирования
M(X-m)2
=D(X)=s2
=sx
2
=s2
(X)
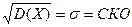 – среднеквадратическое отклонение (стандартное отклонение). – среднеквадратическое отклонение (стандартное отклонение).
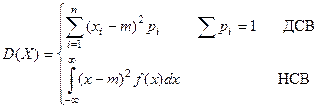
Основные свойства дисперсии:
1. Для любой СВ Х: D(X)³0. При Х=constD(X)º0.
2. D(X)=M(X2
)-M2
(X)=M(X2
-2mX-m2
)
3. D(cX)=c2
D(X)
4. D(X+c)=D(X)
5. D(X+Y)=D(X)+D(Y), D(X-Y)=D(X)+D(Y)
В общем случае:
D(X+Y)=M(X+Y-mx
+
y
)2
=M((X-mx
)+(Y-my
))2
=M((X=mx
)2
+2(X-mx
)(Y-my
)+(Y-my
)2
)=
=D(X)+2M((X-mx
)(Y-my
))+D(Y). Второй член этого выражения называется корреляционным моментом
. mx
+
y
=M(X)+M(Y)=mx
+my
. D(X)=M(X-mx
)2
.
M((X-mx
)(Y-my
))=K(X,Y)=Kxy
=cov(x,y) – ковариация
Kxy
/sx
sy
=rxy
– коэффициент корреляции
6. Независимые СВ: D(XY)=D(X)D(Y)+M2
(X)D(Y)+M2
(Y)D(X)
Дисперсия основных СВ
ДСВ
1. Биноминальные D(X)=npq
2. Пуассоновские D(X)=l
3. Бернуллиевы D(X)=pq
НСВ
1. Равномерно распределенные D(X)=(b-a)2
/12
2. Нормально распределенные D(X)= s2
3. Экспоненциально распределенные D(X)=1/l2
Математическое ожидание и дисперсия суммы случайных величин
X1
,X2
,…,Xn
– независимые СВ с одинаковым законом распределения.
M(Xk)=aD(Xk)=s2
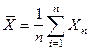 – среднее арифметическое – среднее арифметическое
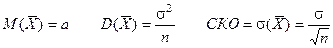
Другие числовые характеристики СВ
Моменты распределения делятся на начальные моменты, центральные и смешанные.
1. Начальные моменты qго
порядка (q=1,2,…): M(X1
)=МО
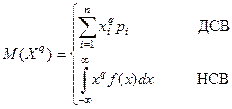
2. Центральные моменты qго
порядка: M((X-m)2
)=D
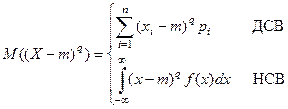
M(x-m)q
=M(x)q
-Cq
1
mM(x)q
-1
+ Cq
2
mM(x)q
-2
+…+(-1)q
mq
M(x-m)3
= M(x)3
-3mM(x)2
+2m3
M(x-m)2
= M(x)2
-m2
=D(x)
Центральные моменты 3го
и 4го
порядков используются для получения коэффициентов асимметрии и эксцесса (As, Ex), характеризующих особенности конкретного распределения.
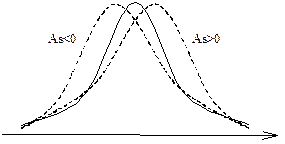 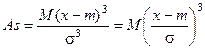
Для нормального закона распределения As=0.
Если As>0, то распределение имеет правостороннюю скошенность
. При As<0 – левосторонняя скошенность
.
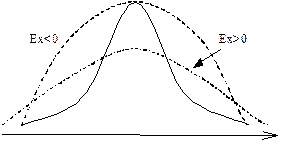 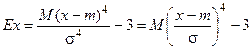
Эксцесс характеризует остро- или плосковершинность исследуемого распределения по сравнению с нормальным распределением.
НСВ:
1. Нормальное распределение: Ex=As=0
2. Равномерное распределение: As=0, Ex=-1,2
3. Экспоненциальное распределение: As=2, Ex=9.
Биноминальное: 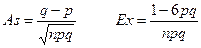
3. Смешанные моменты:
Начальный смешанный момент порядка (k+s) системы 2х
СВ (X+Y):
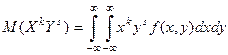
Центральный моменты порядка (k+s):
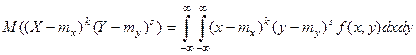
Центральный смешанный момент второго порядка:
Kxy
=M((X-mx
)(Y-my
)) – корреляционный момент
 – коэффициент корреляции – коэффициент корреляции
Мода ДСВ
– значение СВ, имеющее максимальную вероятность.
Мода НСВ
– значение СВ, соответствующее максимуму функции плотности вероятности f(x).
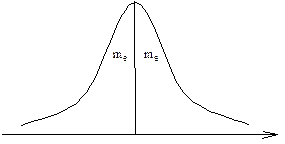 Обозначение моды: m0
, M0
(x), mod(x). Обозначение моды: m0
, M0
(x), mod(x).
Медиана
СВ Х (me
, Me
(x), med(x)) – значение СВ, для которого выполняется равенство:
P(X<me
)=P(X>me
)
F(me
)=0,5.
Медиана – это площадь, получаемая делением фигуры пополам.
В симметричном распределении m=m0
=me
. В несимметричном они не равны.
Так как мода и медиана зависят от структуры распределения, их называют структурными средними
.
Медиана – это значение признака, который делит ранжированный ряд значений СВ на две равных по объему группы. В свою очередь, внутри каждой группы могут быть найдены те значения признака, которые делят группы на 4 равные части – квартиль
.
Ранжированный ряд значений СВ может быть поделен на 10 равных частей – децилей, на 100 – центилей.
Такие величины, делящие ранжированный ряд значений СВ на несколько равных частей, называются квантилями
.
Под p% квантилями понимаются такие значения признака в ранжированном ряду, которые не больше p% наблюдений.
Предельные теоремы теории вероятностей
Делятся на две группы: Закон Больших Чисел (ЗБЧ) и Центральная Предельная Теорема (ЦПТ).
Закон Больших Чисел
устанавливает связь между абстрактными моделями теории вероятностей и основными ее понятиями и средними значениями, полученными при статистической обработке выборки ограниченного объема из генеральной совокупности. P, F(x), M(x), D(x).
ЗБЧ доказывает, что средние выборочные значения при n®¥ стремятся к соответствующим значениям генеральной совокупности: hn
(A)®P, Xср
®M(X), sср
2
®D(X), F*
(X)®F(X).
Лемма Маркова
. Если Y – СВ, принимающая не отрицательные значения, то для любого положительного e:
P(Y³e)£M(x)/e, P(Y<e)³1-M(x)/e.
Доказательство
. Рассмотрим Y и 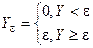 : Ye
£Y, M(Ye
)£M(Y) : Ye
£Y, M(Ye
)£M(Y)
M(Ye
)=0×P(Y<e)+e×P(Y³e)=e×P(Y³e)
M(Y)³M(Ye
)=e×P(Y³e).
Лемма позволяет сделать оценку вероятности наступления события по математическому ожиданию этой СВ.
Неравенство Чебышева
. Для любой СВ с ограниченными первыми двумя моментами (есть МО и D) и для любого e>0:
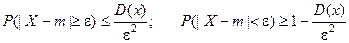
Доказательство
. По лемме Маркова: рассмотрим не отрицательную СВ Y
Y=(X-m)2
M(Y)=M(X-m)2
=D(x)
P(|X-m|³e)=P((X-m)2
³e2
)=P(Y³e2
)£M(Y)/e2
=D(x)/e2
.
Требуется только знание дисперсии СВ при любом законе распределения.
ЗБЧ в форме Чебышева
. X1
, X2
, …, Xn
– последовательность независимых СВ. Для любого e>0 и n®¥:
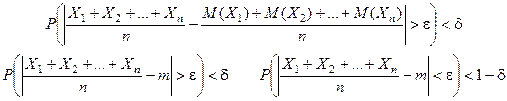
ЗБЧ в форме Бернулли
. m – число успехов в серии из n последовательных испытаний Бернулли. P – вероятность успеха в каждом отдельном испытании. e>0:
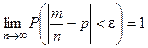
ЗБЧ носит чисто качественный характер. В тех же условиях неравенство Чебышева позволяет получить количественную характеристику оценки вероятности.
Пример
. Для определения вероятности события проведено 40000 опытов. События наблюдалось в m=16042 случаях. За вероятность события принимается относительная частота наступления события: m/n»0,4. Применяя неравенство Чебышева, оценить, с какой вероятностью можно гарантировать, что число 0,4, принятое за вероятность, отличается от истинной вероятности не больше, чем на 0,05.
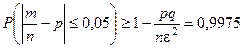
Неизвестные p и q находим из системы уравнений:
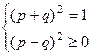 => => 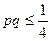
Центральная предельная теорема Ляпунова
.
Предмет внимания этой теоремы – распределение суммы большого числа СВ.
X=(x1
+x2
+…+xn
)/n
Распределение суммы n независимых СВ в независимости от их законов распределения асимптотически сходятся к нормальному закону при неограниченном числе слагаемых и ограниченных двух первых моментах (МО и D).
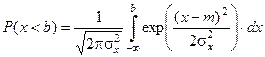
Если si
2
=s2
, то sх
2
=s2
/n,  . .
D(x)=sх
2
=(s1
2
+s2
2
+…sn
2
)/n2
ЦПТ универсальны и справедливы как для НСВ, так и для ДСВ.
P(a<X<b)=Ф(t2
)-Ф(t1
).
t2
=(b-mx
)/sx
t2
=(a-mx
)/sx
Sn
=(X1
+X2
+…+Xn
)/n
P(|Sn
-m|<zs)=2Ф(z)
M(xk)=m D(xk)=s2
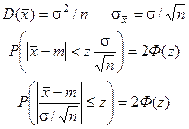
ЦПТ в интегральной форме Муавра-Лапласа
.
Статистическое оценивание параметров распределения
Мы анализируем только выборки из генеральной совокупности. По средне выборочным параметрам находим параметры самой генеральной совокупности.
Задачи такого рода решаются методами проверки статистических гипотез и статистической оценки параметров распределения.
Прежде нужно получить и провести первичную обработку исходных экспериментальных данных.
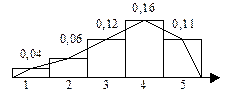 Статистические ряды часто изображают графически в виде полигона, гистограммы, кумулятивной кривой F*
(x). Статистические ряды часто изображают графически в виде полигона, гистограммы, кумулятивной кривой F*
(x).
Полигон
– ломаная линия, соединяющая в декартовой системе координат точки (xi
,ni
), (xi
,mxi
).
Кумулятивная кривая
строится по точкам (xi
,F*
(xi
)).
Гистограмма
– на оси абсцисс – отрезки интервалов t, на этих интервалах строятся прямоугольники с высотой, равной относительной частоте признака. По гистограмме легко строится полигон.
И полигон, и гистограмма характеризуют функцию f*
(x) – плотность вероятности.
НСВ – проблема выбора интервала варьирования h.
h выбирается, исходя из необходимости выявления характерных черт рассматриваемого распределения.
Правило Старджесса
: 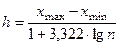
Как только характерные особенности распределения проявились, ставится вопрос об условиях, при которых сформировалось данное распределение – вопрос об однородности статистических данных.
Если функция f*
(x) – бимодальная (имеет два максимума), то статистическое данные неоднородные.
Методы математической статистики должны позволить сделать обоснованные выводы о числовых параметрах и законе распределения генеральной совокупности по ограниченному числу выборок из этой совокупности.
Состав выборок случаен и выводы могут быть ложными. С увеличением объема выборки вероятность правильных выводов растет. Всякому решению, принимаемому при статистической оценке параметров, ставится в соответствие некоторая вероятность, характеризующая степень достоверности принимаемого решения.
Задачи оценки параметров распределения ставятся следующим образом:
Есть СВ Х, характеризуемая функцией F(X, q).
q – параметр, подлежащий оценке.
Делаем m независимых выборок объемом n элементов xij
(i – номер выборки, j – номер элемента в выборке).
1 x11
, x12
, …, x1n
X1
2 x21
, x22
, …, x2n
X2
…
mxm
1
, xm
2
, …, xmn
Xm
Случайные величины X1
, X2
,…Xm
мы рассматриваем как m независимых СВ, каждая из которых распределена по закону F(X, q).
Всякую однозначную функцию наблюдений над СВ х, с помощью которой судят о значении параметра q, называют 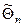 – оценкой параметра
q
. – оценкой параметра
q
.
Выбор оценки, позволяющей получить хорошее приближение к оцениваемому параметру – задача исследования.
Основные свойства оценок
Несмещенность, эффективность и состоятельность.
Оценка 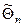 параметра q называется несмещенной
, если M( параметра q называется несмещенной
, если M(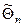 )=q. )=q.
Если 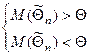 – в оценке параметра q имеется систематическая ошибка. – в оценке параметра q имеется систематическая ошибка.
Несмещенность оценки гарантирует отсутствие систематической ошибки в оценке параметра.
Несмещенных оценок может быть несколько.
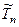 – несмещенная оценка q. – несмещенная оценка q.
Разброс параметров или рассеяние величины относительно математического ожидания q характеризует дисперсия D(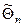 ), D( ), D(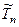 ). ).
Из двух или более несмещенных оценок предпочтение отдается оценке, обладающей меньшим рассеянием относительно оцениваемого параметра.
Оценка 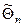 называется состоятельной
, если она подчиняется закону больших чисел: называется состоятельной
, если она подчиняется закону больших чисел:
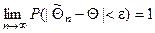
На практике не всегда удается удовлетворить одновременно всем трем требованиям.
Оценка математического ожидания по выборке
Теорема 1
. Среднее арифметическое 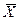 по n независимым наблюдениям над СВ x с МО m является несмещенной оценкой этого параметра. по n независимым наблюдениям над СВ x с МО m является несмещенной оценкой этого параметра.
Доказательство: x1
,x2
,…,xn
M(x)=mM(x1
)=M(x2
)=…=M(xn
)=m
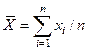 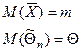
Теорема 2
. Среднее арифметическое 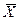 по n независимым наблюдениям над СВ x с МО m и дисперсией D(x)=s2
является состоятельной оценкой МО. по n независимым наблюдениям над СВ x с МО m и дисперсией D(x)=s2
является состоятельной оценкой МО.
Доказательство: D(x)=s2
D(x1
)=D(x2
)=…=D(xn
)=s2
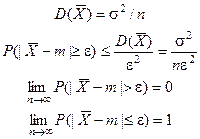
Теорема 3
. Если СВ Х распределена по нормальному закону с параметрами (m,s2
), то несмещенная и состоятельная оценка 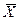 МО m имеет минимальную дисперсию s2
/n => МО m имеет минимальную дисперсию s2
/n => 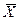 является и эффективной. является и эффективной.
Оценки дисперсии по выборке
Если случайная выборка состоит из n независимых наблюдений над СВ Х с M(X)=m и D(X)=s2
, то выборочная дисперсия не является несмещенной оценкой дисперсии генеральной совокупности.
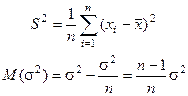
Несмещенной оценкой D(x) является 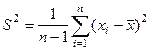 , , 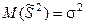 . .
Легко доказать по формуле Чебышева, что оценки S2 и 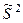 являются состоятельными оценками дисперсии. являются состоятельными оценками дисперсии.
Несмещенная, состоятельная и эффективная оценка дисперсии:
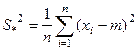
Если МО генеральной совокупности неизвестно, то используют 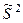 . .
Существуют регулярные методы получения оценок параметров генеральной совокупности по данным выборок.
Методы оценки параметров генеральной совокупности
Метод наибольшего (максимального) правдоподобия (МНП)(ММП)
обладает следующими достоинствами:
1. Всегда приводит к состоятельным оценкам (иногда смещенным)
2. Получаемые оценки распределены асимптотически нормально и имеют минимально возможную дисперсию по сравнению с другими асимптотически нормальными оценками.
Недостаток: требуется решать громоздкие системы уравнений.
Имеется СВ Х, f(x,q) – функция ее плотности вероятности, выражение которой известно.
q – неизвестный параметр, подлежащий оценке.
x1
, x2
,…,xn
– n независимых наблюдений над СВ x.
В основе МНП лежит функция L(q) – функция правдоподобия, формирующаяся с учетом свойств многомерной функции распределения наблюдений над СВ х.
f(x1
, x2
,…,xn
,q)=f(x1
, q)×f(x2
,q)×…×f(xn
,q)
В указанное равенство подставляются данные и получаем функцию L(q):
L(q)=f(x1
, q)×f(x2
,q)×…×f(xn
,q)
За максимальное правдоподобное значение параметра q принимаем 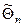 , при которой L(q) максимально. , при которой L(q) максимально.
L'(q)=0 => qmax
=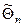
Метод моментов(Метод Пирсона).
Метод обладает следующими достоинствами:
1. Оценки получаемые этим методом всегда являются состоятельными.
2. Метод моментов мало зависит от закона распределения случайной величины.
3. Сложность вычисления незначительна.
Известна случайная величина Х, которая характеризуется f(x, θ1
, θ2
…θq
), аналитический вид этой функции известен.
По выборке объёмом n х1
,х2
,х3
,…хn
– значения случайной величины в выборке вычисляем эмпирические начальные моменты случайной величины:
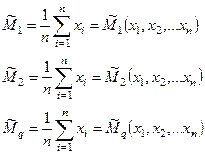
Находим теоретические моменты:
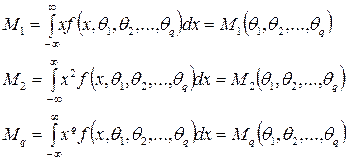
Основная идея метода моментов заключается в приравнивании значения эмпирических значений моментов теоретическим.
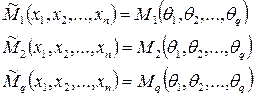
Решим систему q-уравнений с q-неизвестными:
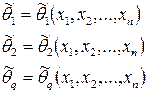 состоятельные оценки. состоятельные оценки.
Состоятельность этих оценок основана на том, что эмпирические моменты при достаточно большом n (n→∞) стремится к теоретическим. Выполняется закон больших чисел.
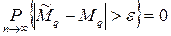
Распределение средней арифметической для выборки
из нормальной совокупности. Распределение Стьюдента.
Выборочное среднее рассчитанное по конкретной выборке, есть конкретное число. Состав выборки случаен и среднее арифметическое вычисленное по элементам другой выборки того же объёма, будет число отличное от первого.
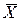 - средняя арифметическая величина меняющаяся от выборки к выборке. - средняя арифметическая величина меняющаяся от выборки к выборке.
Теорема:
Если случайная величина Х подчиняется нормальному закону с параметрами m и σ2
Х(m, σ2
), а х1
,х2
,х3
,…,хn
– это выборка из генеральной совокупности, то средняя арифметическая:
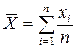
так же является случайной величиной подчиняющаяся нормальному закону с параметрами m и σ2
/n, а нормированная случайная величина:
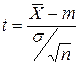
так же подчиняется нормальному закону с параметрами (0;1).
Предполагается при использовании таблиц интеграла вероятности, что объём выборки n достаточно велик(n ≥ 30).
Существует достаточно большое количество технических задач в которых не удаётся собрать выборку такого объёма. Тем не менее анализу такой выборки необходимо дать вероятностную оценку.
В 1908 году английский математик Вильям Госсет дал решение задачи малых выборок (псевдоним Стьюдент). Стьюдент показал, что в условиях малых выборок надо рассматривать не распределение самих средних, а их нормированных отклонений от средних генеральных.
Надо рассматривать:
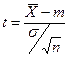
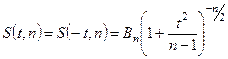 - это чётное распределение. - это чётное распределение.
Оно зависит только от объёма выборки n и не зависит ни от математического ожидания, ни от дисперсии случайной величины Х. При n→∞ t – распределение Стьюдента переходит в нормальное распределение.
Поскольку в большинстве случаев σ генеральной совокупности неизвестно, то работает с такой величиной:
- состоятельная и несмещённая оценка.
Существуют t таблицы распределения Стьюдента.
Величина доверительной вероятности, её выбор находятся за пределами прикладной статистики. Они задаются самим исследователем. Величина доверительной вероятности определяется тяжестью тех последствий, которые могут произойти в случае, если произойдёт нежелательное событие.
Величина tn
,
p
показывает предельную случайную ошибку расхождения средневыборочного и математического ожидания.
Распределение дисперсии в выборках нормальной совокупности.
Распределение χ2
Пирсона.
Выборочная дисперсия так же является случайной величиной меняющейся от выборки к выборки.
1) М(Х) – известно;
2) М(Х) – не известно.
1) Имеется случайная величина Х, которая подчиняется нормальному закону с параметрами (m, σ2
),
где: хi
(i = 1, 2, …, n) – независимые наблюдения над случайной величиной.
Для дисперсии мы выбираем вот такую оценку:
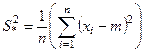 - несмещённая, состоятельная и эффективная оценка дисперсию генеральной совокупности. - несмещённая, состоятельная и эффективная оценка дисперсию генеральной совокупности.
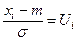
Величина Ui
является случайной величиной с параметрами (0;1).
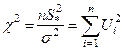
Случайная величина представляющая собой сумму квадратов n независимых случайных величин, каждая из которых подчиняется нормальному закону распределения с параметрами (0;1) и независимых случайных величин с распределением χ2
с к = n – степенями свободы.
Сама функция плотности вероятности f(χ2
) имеет вид:
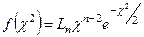
Эта функция зависит только от объёма выборки и не зависит ни от математического ожидания, ни от дисперсии, ни от х.
Имеются таблицы распределения χ2
позволяющие вычислить вероятность события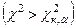
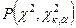 , ,
где: к – число степеней свободы;
α – доверительная вероятность, которая задаётся самим исследователем.
2) Математическое ожидание неизвестно
.
Когда случайная величина Х с параметрами (
m
,
σ
2
) – неизвестны.
Для оценки дисперсии генеральной совокупности используется величина:
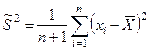
Случайная величина 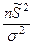 имеет распределение χ2
с к = n – 1 степенями свободы. имеет распределение χ2
с к = n – 1 степенями свободы.
Уменьшение степени свободы использована для получения среднего выборочного.
Доверительный интервал.
Рассмотренные ранее оценки получили название точечных оценок. На практике широко используются интервальные оценки, для получения которых используется метод доверительных интервалов.
В методе доверительных интервалов указывает не одно(точечное) значение интересующего нас параметра, а целый интервал. Он строится на основе неравенства Чебышева:
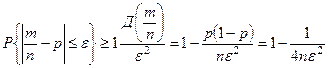
Задаётся некоторое число 0 < α < 1 близкое к нулю, которое называется уровень значимости
.
Параметр ε находится из неравенства:
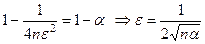 , тогда: , тогда:
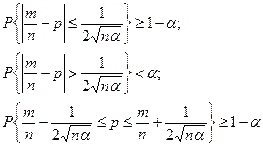
Интервал 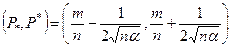 называется доверительным интервалом с уровнем значимости α
. называется доверительным интервалом с уровнем значимости α
.
Доверяясь расчёту мы утверждаем, что неизвестная вероятность принадлежит указанному интервалу, а вероятность возможной ошибки имеющей место тогда, когда этот интервал не накрывает истинное значение α не превосходит уровня значимости α.
n = 1000, m/n = 0,6
При α = 0,1 (0,550; 0,650)
При α = 0,01 (0,442; 0,758)
Истинное значение вероятности Р мы незнаем, но можем утверждать, что первый интервал накрывает это значение с вероятностью не менее чем 0,9 , а второй – 0,99.
Пример
. Имеется некоторое предположение, гипотеза, о том, что неизвестная вероятность Р равна заданному число Р0
:
Н0
: р = р0
; (Р0
= 0,5).
Эту гипотезу можно принять, а можно и отклонить посчитав её противоречащей известным статистическим данным.
Для принятия решения(проверки гипотезы) мы проделаем следующую процедуру:
Если Р0
Î(Р*
, Р*
) с α, то гипотезу принимаем(возможно здесь и ошибка, мы можем принять ложную гипотезу – такая ошибка первого рода).
Если Р0
Ï (Р*
, Р*
) с α, то гипотеза отвергается(здесь тоже можем совершить ошибку отклонить верную гипотезу – такая ошибка второго рода, вероятность такой ошибки заранее задаётся нами при построении доверительного интервала).
При наших предположениях, когда уровень значимости равен 0,1 в общем мы имеем Р0
Ï (0,550; 0,650). Эта гипотеза отвергается, при этом мы ошибаемся не более чем в 1 случае из 10.
Построение доверительного интервала для математического ожидания.
Случайная величина Х распределённая с параметрами (m, σ2
).
Математическое ожидание неизвестно и требуется построить для него доверительный интервал.
1. Известно σ2
.
2. Неизвестно σ2
.
1.
σ2
известно.
Проводится выборка из генеральной совокупности и в качестве несмещённой, состоятельной и эффективной оценки математического ожидания выбирается 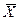 . Оно тоже подчиняется нормальному закону с параметрами: . Оно тоже подчиняется нормальному закону с параметрами:
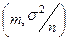 , где: n – объём выборки. , где: n – объём выборки.
Нормированная величина:
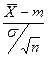
подчиняется нормальному закону распределения с параметрами (0; 1), тогда вероятность:
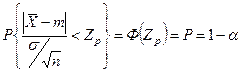
Вероятность задаётся уровнем α, величина Р – доверительная вероятность. По таблице находим величину Zp
.
При известном Zp
получим:
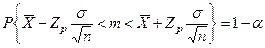
Интервал для математического ожидания (m*
; m*
) получим:
– доверительный интервал для математического ожидания с уровнем значимости α
.
2. σ2
неизвестно.
Точно так же проводится выборка объёмом n, формируется случайная величина t
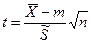
Случайная величина t имеет распределение Стьюдента.
Зная объём выборки n, задаваясь уровнем значимости α или задаваясь доверительной вероятностью р=1-α.
По распределению Стьюдента находим tn
,
p
– максимальное отклонение m и 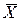 . .
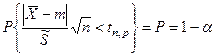
где: Р – доверительная вероятность.
Отсюда легко строится доверительный интервал.
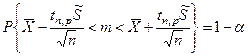
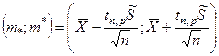
Несмотря на кажущиеся совпадения двух формул они существенно отличаются друг от друга.
Во втором случае величина доверительного интервала зависит не только от доверительной вероятности, но и от объёма выборки.
Это различие наиболее существенно проявляется при малых выборках.
Построение доверительного интервала для дисперсии.
Случайная величина Х распределена по нормальному закону с параметрами (m, σ2
).
Требуется построить доверительный интервал для дисперсии по выборочным дисперсия.
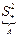 или или 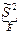
Построение доверительного интервала для дисперсии основывается на том, что случайные величины:
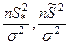 – имеют распределение χ2
с – имеют распределение χ2
с
к = n, к = n – 1 – степенями свободы.
При заданной доверительной вероятности 1 – α мы записываем:
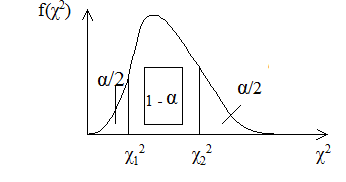 
По таблице распределения χ2
мы должны выбрать такие два числа  , чтобы площадь заштрихованная была равна 1-α. , чтобы площадь заштрихованная была равна 1-α.
Обычно величины  выбирают таким образом, чтобы выполнялось неравенство: выбирают таким образом, чтобы выполнялось неравенство:
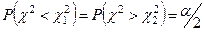
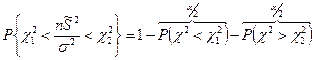
В таблице распределения χ2
имеется только вероятность вида:
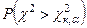
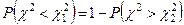
Тогда:
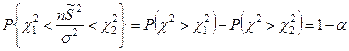
Преобразуя это неравенство получим:
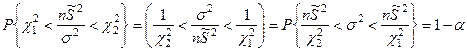
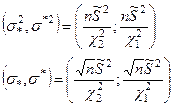 - доверительный интервал с уровнем значимости α. - доверительный интервал с уровнем значимости α.
Проверка статистических гипотез.
Наряду с оценкой параметров распределения по выборочным данным большой интерес представляет вид (закон) распределения неизвестный на практике. Такие задачи решаются методами статических гипотез.
Относительно неизвестного теоретического распределения формируется некоторое предположение, которое формируется в виде гипотез.
Например, теоретическое распределение подчиняется нормальному, экспоненциальному закону.
При проверки гипотез используется принцип значимости основывающийся на принципе практической невозможности.
Согласно принципу практической невозможности события с очень малыми вероятностями в практических приложениях считаются невозможными.
Максимум таких вероятностей определяет уровень значимости α, который задаётся.
В свою очередь согласно принципу значимости отвергается случайность появления практически невозможного события.
Поскольку теоретическое распределение задано гипотезой, то легко рассчитать вероятность появления некоторого события при проведении испытаний или взятии выборки и пусть такая расчётная вероятность не превышает ε, т.е. событие является практически невозможным.
Если же такое событие происходит, то возникает противоречие между выдвинутой гипотезой и выборкой. Гипотезу следует отвергнуть в этом и заключается содержание принципа значимости.
Проверяемая гипотеза называется нулевой или основной Н0
.
Если гипотеза отвергается, то принимается противопоставляемая ей гипотеза Н1
, которая называется конкурирующей ил альтернативной.
Про проверки гипотезы Н0
возможны ошибки.
Можно отвергнуть гипотезу Н0
в условиях когда она верна и совершить ошибку I-го рода и можно принять гипотезу, когда она не верна и совершить ошибку II-го рода.
Решение поставленной задачи по сути дела состоит в разделении всего множества выборочных данных на 2-а не пересекающихся подмножества О и W. Таких, что решение принимается в пользу гипотезы Н0
, если выборка принадлежит области О и в пользу гипотезы Н1
, если выборка принадлежит подмножеству W. Область W называется критической областью выборочного пространства. Здесь гипотеза Н0
отвергается, а область О является областью допустимых значений. Здесь гипотеза Н0
принимается.
Проверка гипотезы о равенстве центров распределения математического ожидания 2-х нормальных генеральных совокупностей.
Задача имеет большой практический интерес. Достаточно часто наблюдается такая ситуация, что средний результат в одной серии эксперимента отличается от среднего результата в другой серии эксперимента.
Возникает вопрос: можно ли объяснить отличительное расхождение случайными ошибками эксперимента и относительно малыми объёмами выборки или это отклонение вызвано какими-либо неизвестными, незамеченными закономерностями.
Имеется две случайных величин Х и Y с нормальным законом распределения.
Получим 2-е независимых выборки объёмом n1
и n2
из указанных генеральных совокупностей.
Необходимо проверить: Н0
: М(X) = М(Y)
H1
: |M(X) – M(Y)| > 0
Рассмотрим два случая:
1. – известны дисперсия генеральной совокупности 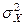 ; ;
2. – дисперсия неизвестна 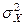 . .
1
- 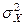 , ,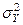 M(X) и M(Y) - неизвестны, для их оценки мы используем средние выборочные M(X) и M(Y) - неизвестны, для их оценки мы используем средние выборочные 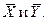
Относительно 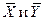 известно, что они подчиняются нормальному закону распределения с параметрами:
известно, что они подчиняются нормальному закону распределения с параметрами:
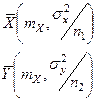
Рассмотрим случайную величину 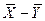 . В силунезависимости выборок эта случайная величина подчиняется нормальному закону распределения.
. В силунезависимости выборок эта случайная величина подчиняется нормальному закону распределения.
Её дисперсия:
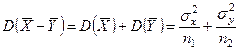
Если гипотез Н0
верна(справедлива), то тогда: 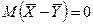 . .
Величина:
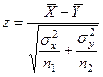 с параметрами (0, 1) с параметрами (0, 1)
Выбирая уровень значимости α или доверительную вероятность Р = 1- α можем записать:
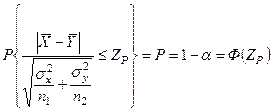 ; ; 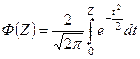 ; ;
Выбирая по величине интеграла вероятности значения ZP
мы тем самым делим выборочных данных на область допустимых значений и критическую область.
Для области, где выполняется неравенство |Z| ≤ ZP
– область допустимых значений(ОДЗ) Н0
– принимается.
А, если |Z| > ZP
– критическая область(КО) Н0
– отвергается, Н1
– принимается.
Чем меньше α, тем меньше вероятность отклонить проверяемую гипотезе, если она верна. Но в этом случае увеличивается вероятность совершения ошибки II-го рода.
Чем меньше α, тем больше ОДЗ и тем больше вероятность принять проверяемую гипотезу, если она не верна, т.е. совершить ошибку II-го рода.
Методы проверки гипотез позволяют только отвергнуть проверяемую гипотезу, но они не могут доказать её справедливость.
2
-Дисперсия неизвестна.
Есть 2-е случайных величины X и Y, 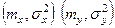 . .
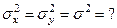 mx
и my
неизвестны берутся независимые выборки (n1
;n2
) и рассматривается гипотеза: Н0
: M(X) = M(Y) mx
и my
неизвестны берутся независимые выборки (n1
;n2
) и рассматривается гипотеза: Н0
: M(X) = M(Y)
H1
: |M(X) – M(Y)| > 0.
Для оценки математического ожидания M(X) и M(Y) используем среднее выборочное 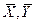 . Для оценки дисперсий используем: . Для оценки дисперсий используем:
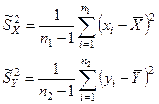 - несмещённые, состоятельные оценки дисперсии. - несмещённые, состоятельные оценки дисперсии.
Поскольку генеральные совокупности X и Y имеют одинаковые дисперсии, то для оценки дисперсии 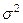 целесообразно использовать результаты обеих выборок. целесообразно использовать результаты обеих выборок.
Наиболее целесообразной оценкой дисперсии является средняя взвешенная этих двух оценок.
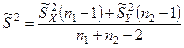
Если гипотеза Н0
справедлива, то тогда случайная величина 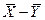 подчиняется нормальному закону распределения с подчиняется нормальному закону распределения с 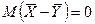 и с дисперсией и с дисперсией 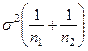
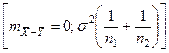
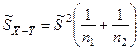
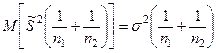
Если построить случайную величину:
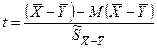
, то она будет подчиняться нормальному закону с параметрами (0; 1).
Т.к. 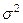 неизвестна, то такая величина подчиняется t-распределению Стьюдента(со степенями свободы n1
+ n2
– 2). неизвестна, то такая величина подчиняется t-распределению Стьюдента(со степенями свободы n1
+ n2
– 2).
Для α(Р = 1– α) подсчитывается критическое значение 
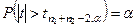
Если вычисленные значения 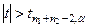 , то гипотеза Н0
отвергается и наоборот: , то гипотеза Н0
отвергается и наоборот:
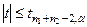 Н0
принимается. Н0
принимается.
Проверка гипотезы о совпадении 2-х дисперсий.
Задача имеет важное практическое значение. Возникает при наладке какого-либо оборудования при сравнении точности приборов, инструментов, методов измерений.
По 2-м независимым выборкам вычислены оценки дисперсий:
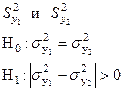
Для проверки гипотезы Н0
используется критерий Фишера(F–критерий, F–распределение).
Вычисляется коэффициент:
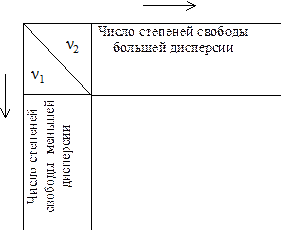 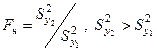
Вычисляется критическое значение Fкр
(α (или Р = 1 - α))
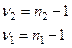
,где: ν – число степеней свободы числителя и знаменателя.
Если Fн
> Fкр
, то Н0
отвергается,
Fн
< Fкр
, то Н0
принимается.
Анализ однородности дисперсий.
Понятие однородности
является обобщением понятия равенства дисперсий в случае, если число выборок превосходит 2(N > 2).
Для проверки гипотезы H0
:
Н0
: 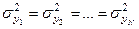
Н1
: дисперсия неоднородна.
Объёмы выборок n1
,n2
, … ,nN
различны.
Когда объёмы выборок различны для решения задачи является χ2
с (N-1) степенями свободы.
На практике наиболее частым является когда объёмы выборок одинаковы.
При равных объёмах выборок используется критерий Кохрана для проверки Н0
.
Есть соответствующее распределение, но оно громоздко.
В начале вычисляется фактическое значение критерия:
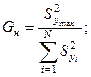
Отношение максимальной оценки дисперсии к сумме всех оценок дисперсий вычисленных по табличным данным.
Для Р = 1 – α вычисляется критическое значение критерия Кохрана Gкр
.
При Gн
≤ Gкр
- H0
принимается;
Gн
> Gкр
- H0
отвергается.
Проверка гипотез о законе распределения.
Имеется случайная величина Х, требуется проверить гипотезу Н0
:
Н0
: эта случайная величина подчиняется некоторому закону распределения F(x).
Для проверки гипотезы делается выборка состоящая из n независимых наблюдений над случайной величиной Х. По выборке строится эмпирическая функция распределения F*(x). Сравнивая эти распределения с помощью некоторого критерия(критерий согласия) делается вывод о том, что эти два распределения согласуются, т.е. Н0
– принимается.
Существует несколько критериев согласия: χ2
Пирсона, критерий Колмогорова и т.д.
Критерий согласия χ2
Пирсона.
Имеется случайная величина Х, выдвигается гипотеза Н0
: F(x), делается выборка.
Диапазон Хmin
– Хmax
разбивается на ℓ интервалов. Размер интервала определяется по правилу Старджесса. D1
;D2
;D3
;…;Dℓ
.
| Интервал Di
|
D1
|
D2
|
D3
|
… |
Dℓ
|
| Эмпирическая частота mi
|
m1
|
m2
|
m3
|
… |
mℓ
|
| Теоретическая частота npi
|
np1
|
np2
|
np2
|
… |
npℓ
|
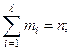
mi
> 3(в среднем 5 - 7).
При mi
< 3 укрупнить интервал.
Находим частоту попадания случайной величины внутрь каждого интервала.
Поскольку теоретическое распределение задано в гипотезе Н0
всегда можно найти вероятность pi
попадания случайной величины внутрь каждого интервала.
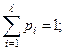
χ2
Пирсона предполагает, что надо построить:
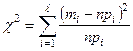
(имеет распределение χ2
только при относительно больших n (n > 50)).
Порядок применения χ2
Пирсона:
1. Рассчитывается эмпирическое значение критерия χ2
;
2. Выбирается уровень значимости α (при Р = 1 - α);
3. По таблице подсчитывается 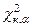 , ,
где: α – уровень значимости;
к – число степеней свободы.
В общем случае к = ℓ - r – 1,
где: ℓ - количество интервалов разбиения;
r – количество параметров распределения подсчитанных по выборке;
Здесь к = r – 1.
Если 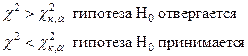
Критерий Колмогорова.
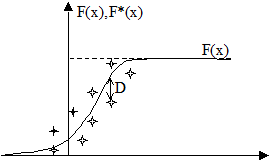
По результатам выборки объёмом n строится эмпирическая функция распределения F(х). Принимается гипотеза Н0
: случайная величина Х подчиняется распределению описанному функцией F(x).
За меру расхождения функций принимается величина:
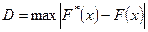
Существуют таблицы распределения Колмогорова в которых можно найти:
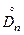 - критическое значение. Оно зависит от уровня значимости α(Р = 1 - α), величины в и величины выборки n. - критическое значение. Оно зависит от уровня значимости α(Р = 1 - α), величины в и величины выборки n.
Если полученные из опыта значения коэффициента в оказывается больше критического 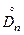 , то Н0
отвергается. , то Н0
отвергается.
Если 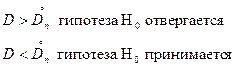
С помощью величины 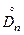 можно построить доверительные границы для неизвестной функции F(x): можно построить доверительные границы для неизвестной функции F(x):
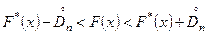
Колмогоров показал, что при n → ∞ величина:
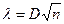
подчиняется распределению Колмогорова.
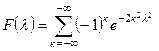
Критерий Колмогорова так же может быть использован для статистической проверки принадлежности двух выборок объёмом n1
и n2
к одной и той же генеральной совокупности. Вычисляется параметр λ:
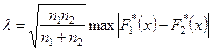
где: 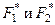 - эмпирические функции распределения соответственно первой и второй выборки. - эмпирические функции распределения соответственно первой и второй выборки.
По величине λ судят о согласии.
Раздел 6.
Основы дисперсионного анализа.
Дисперсионный анализ
– это статистический метод анализа результатов наблюдений зависящий от различных одновременно действующих факторов и позволяющий выбрать из ряда факторов наиболее важные, оценивать их влияние.
Основными предпосылками дисперсионного анализа является как правило нормальное распределение результатов наблюдений и отсутствие влияния исследуемых факторов на дисперсию результатов наблюдения.
Обязательным здесь является возможность управляемого изменения фактора в рамках его разновидностей называется уровнями фактора
.
Эти эксперименты могут быть пассивными, когда существование уровней и их смена является естественными для исследуемого объекта и активными, когда эти изменения искусственно вносятся экспериментатором по заранее составленному плану.
Идея дисперсионного анализа в разложении общей дисперсии случайной величины на независимые случайные слагаемые, каждый из которых характеризует влияние того или иного фактора, или их взаимодействие. Последующие сравнения этих дисперсий позволяют оценить сущность влияния факторов на исследуемую величину.
Пусть Х – это некоторая случайная величина зависящая от 2х
действующих на неё факторов А и В.
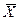 - среднее значение исследуемой величины. - среднее значение исследуемой величины.
Отклонение:
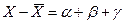
где: α – отклонение вызванное фактором А;
β – отклонение вызванное фактором В;
γ - отклонение вызванное другими факторами.
α, β, γ – случайные величины независимы.
Дисперсию случайной величины Х, α, β, γ обозначим:
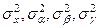
где: величина 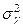 - остаточная дисперсия учитывающая влияние случайных и прочих неучтённых факторов. - остаточная дисперсия учитывающая влияние случайных и прочих неучтённых факторов.
Для независимых и случайных величин имеет место равенство:
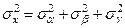
Сравнивая 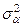 или или 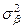 с величиной с величиной 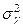 можно установить степень влияния факторов А и В на величину Х по сравнению с неучтёнными и случайными факторами. можно установить степень влияния факторов А и В на величину Х по сравнению с неучтёнными и случайными факторами.
Сравнивая между собой 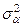 и и 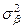 мы можем оценить сравнительную степень влияния факторов А и В на величину Х. мы можем оценить сравнительную степень влияния факторов А и В на величину Х.
Дисперсионный анализ позволяет на основании выборочных данных найти все значения дисперсии 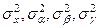 . Далее используя соответствующие критерии можно оценить степень влияния параметров А и В на исследуемую случайную величину. . Далее используя соответствующие критерии можно оценить степень влияния параметров А и В на исследуемую случайную величину.
Если речь идёт о влиянии одного фактора на исследуемую случайную величину, то речь идёт об однофакторном дисперсионном анализе. Если же речь идёт о многих факторах, то говорят о многофакторном дисперсионном анализе.
Однофакторный дисперсионный анализ.
Большое количество практических задач приводится к задачам однофакторного дисперсионного анализа.
Типичным примером является работа технологической линии в составе которой имеется несколько параллельных рабочих агрегатов.
На выходе имеют место какие-то детали. Эти детали по какому-то параметру можем контролировать.
Ясно, что среднее значения контролируемых параметров после каждого станка будут несколько отличаться.
Вопрос:
Обусловлены ли эти отличия действием случайных факторов или имеет место влияние конкретного станка агрегата.
В данном случае фактор только один – станок.
Совокупность размеров деталей подчиняется нормальному закону распределения, и все эти совокупности имеют равные дисперсии.
Имеется m станков, т.о. имеется m совокупностей. Из этих совокупностей мы проводим выборки объёмом n. Так, что значение параметров i-той совокупности i: 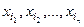 . .
Все выборки можно записать в виде таблицы, которая называется матрицей наблюдения.
Выдвигаем гипотезу Н0
заключающуюся в равенстве средних выборочных.

Гипотеза Н0
проверяется сравнением внутригрупповых и межгрупповых дисперсий по F критерию Фишера.
Если расхождение незначительно, то принимается гипотеза Н0
, в противном случае гипотеза Н0
отвергается.
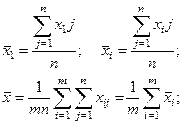
Далее находят сумму квадратов отклонений от общего среднего:
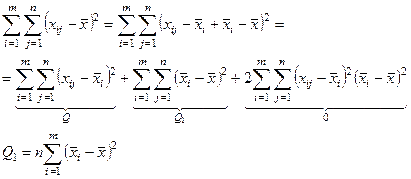
Ноль потому, что стоит сумма от 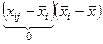 - сумма отклонений переменных одной совокупности от средней арифметической той же совокупности. - сумма отклонений переменных одной совокупности от средней арифметической той же совокупности.
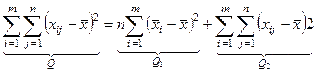
Слагаемое Q1
является суммой квадратов разностей между средними отдельных совокупностей и общей средней всех совокупностей. Эта сумма называется суммой квадратов отклонений между группами. Она характеризует систематическое отклонение между совокупностями наблюдений.
Величину Q1
– рассеяние по фактору.
Слагаемое Q2
– представляет собой сумма квадратов разностей между отдельными и средней соответствующей совокупности. Эта сумма называется суммой квадратов отклонений внутри группы.
Она характеризует остаточное рассеяние случайных погрешностей совокупностей.
Величина Q называется общей или полной суммой квадратов отклонений отдельных отклонений от общей средней.
Получим оценки дисперсий: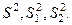
- дисперсия обусловленная влиянием фактора;
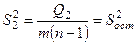 - остаточная дисперсия – влиянием случайных и других неучтённых факторов. - остаточная дисперсия – влиянием случайных и других неучтённых факторов.
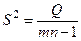 - полная дисперсия. - полная дисперсия.
Далее формируем оценку различия между оценками 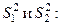
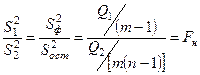 подчиняется распределению f
2
Фишера. подчиняется распределению f
2
Фишера.
Выбираем уровень значимости α, или доверительной вероятности 1– α = Р и по таблице F-распределения с числом степеней свободы: к1
= m–1; к2
= m(n–1) находим критическое значение  Фишера. Фишера.
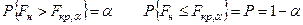
Сравнивая между собой Fн
и Fкр,α
мы делаем вывод насколько сильно влияние интересующего нас фактора на исследуемую случайную величину.
В этом и состоит идея дисперсионного анализа.
Однофакторный дисперсионный анализ обычно представляют в виде таблицы.
| Компоненты дисперсии |
Оценки дисперсии |
Число степеней свободы |
| Основной фактор |
Межгрупповая дисперсия |
 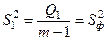 |
m - 1 |
| Случайные, неучтенные факторы |
Внутригрупповая дисперсия |
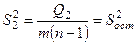 |
m(n - 1) |
| Общая дисперсия |
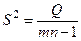 |
mn - 1 |
Основы регрессионного и корреляционного анализа.
Связи между различными явлениями в природе сложны и многообразны. В технике чаще всего речь идет о функциональной зависимости. В большинстве случаев интересующие нас явления протекают в условиях воздействия на них множества неконтролируемых факторов. Воздействие каждого из этих факторов в целом невелико, при этом связь теряет строгую функциональность и система переходит не в строго определенное состояние, а в одно из множества возможных. Речь идет о стохастической связи.
Под стохастической
мы понимаем такую связь, когда одна случайная переменная реагирует на изменения другой случайной переменной изменением своего закона распределения.
Наиболее широко в технике используется частный случай стохастической связи, называемый статистической связью
, при которой условное МО некоторой случайной величины Y является функцией от значения, которое принимает другая случайная величина X:
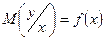
Как правило исследуются такие виды статистической связи, при которых значение некоторой случайной переменной зависит в среднем от значений, принимаемых другой случайной переменной:
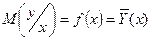
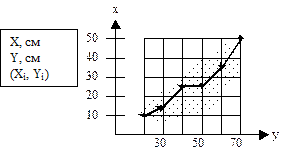 Такое представление зависимости между переменными X и Y называется полем корреляции. Можно также построить таблицу корреляции. Такое представление зависимости между переменными X и Y называется полем корреляции. Можно также построить таблицу корреляции.
Проделывая операцию усреднения для всех тех значений Х, по которым есть экспериментальный материал, приходим к тому, что облако исчезает и получается набор точек, представляющих средние значения. Соединяя эти точки, получаем ломанную, называемую эмпирической линией регрессии
.
Связь между СВ характеризуется формой и теснотой связи.
Определение фориы связи и понятие регрессии.
Определить форму связи между СВ – значит выявить механизм получения зависимой случайной величины. При изучении статистических связей, форму связей характеризует функция регрессии:
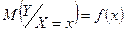 - зависимость условного МО - зависимость условного МО
Если св Х и Y зависимы, то МО их произведения:
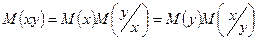
Регрессия св Y относительно Х определяется как:
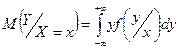 , ,
где 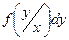 - условная плотность вероятности по формуле Байеса: - условная плотность вероятности по формуле Байеса:
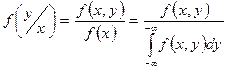
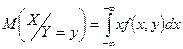 - регрессия Х по Y. - регрессия Х по Y.
Функция регрессии имеет важное практическое значение. Она может быть использована для прогноза значений, которые может принимать известная случайная величина при ставших известными значениях другой случайной величины.
Точность прогноза определяется дисперсией условного распределения:
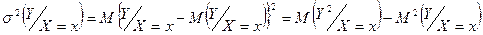
учитывая: 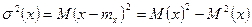
Несмотря на важность функции регрессии, возможности ее практического использования ограничены, т.к. для ее вычисления необходимо знать аналитический вид двумерной функции {x,y}. Мы же, как правило, имеем выборку ограниченного объема.
Традиционный путь приводи к большим ошибкам, т.к. одну и ту же совокупность точек на плоскости можно описать с помощью различных функций.
Другой характеристикой формы связи, используемой на практике, стала кривая регрессии
– зависимость условного среднего случайной величины от значения, которое принимает случайная величина Х: 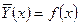 . .
Определение кривой регрессии инвариантно закона совместного распределения св Х и Y. Важное значение в практике имеет двумерный нормальный закон распределения
. Особенностью этого распределения является то, что условные МО совпадают с условными средними. При этом функция регрессии совпадает с кривой регрессии.
Линейная регрессия (ЛР). Метод наименьших квадратов.
Линейная регрессия занимает в технике и теории корреляции особое место. Она обусловлена двумерным нормальным законом распределения СВ Х и Y:
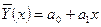 , где , где
а0
и а1
– коэффициенты регрессии,
х – независимая случайная величина
Параметры уравнения регрессии определяются методом наименьших квадратов, предложенным Лагранжем и Гауссом, который сводится к следующему.
Строятся квадратичные формы:
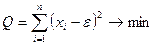
xi
– измеренное значение переменной,
e - истинное или теоретическое значение этой величины.
Требуется, чтобы сумма квадратов отклонений измеренных значений относительно истинных была минимальна.
В случае линейной регрессии за теоретическое значение принимается значение 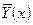 , т.е. ищется такая прямая линия с коэффициентами а0
и а1
, чтобы сумма квадратов отклонений от этой линии была минимальна. , т.е. ищется такая прямая линия с коэффициентами а0
и а1
, чтобы сумма квадратов отклонений от этой линии была минимальна.
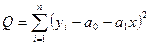 , ,
уi
– измеренное значение переменной Y.
Минимальные квадратичные формы получают, приравнивая к нулю ее производные по а0
и а1
:
 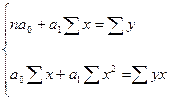
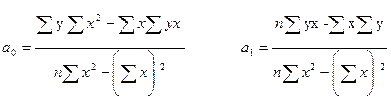
Нелинейная регрессия (НР).
Форма связи между условными средними определяется уравнениями регрессии. В зависимости от вида уравнений можно говорить о ЛР или НР.
В общем случае эта зависимость может быть представлена в виде полинома степени k:
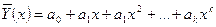
Определение коэффициентов регресии производится по методу наименьших квадратов:
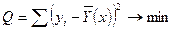
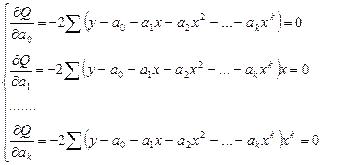
В результате получаем систему нормированных уравнений:
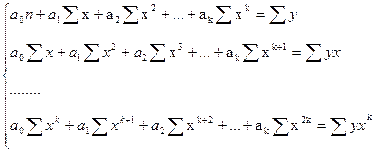
Решая полученную систему известным способом, находим коэффициенты регрессии.
Измерение тесноты связи.
Если бы величина Y полностью определялась аргументом Х, все точки лежали бы на линии регрессии. Чем сильнее влияние прочих факторов, тем дальше отстоят точки от линии регрессии. В случае в) связь между Х и Y является более тесной.
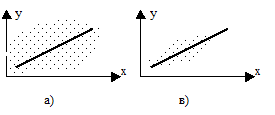
За основу показателя, характеризующего тесноту связи, берется общий показатель изменчивости дисперсии:
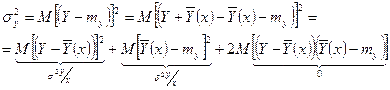
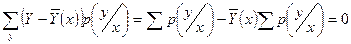
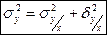 (*) (*)
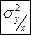 - дисперсия переменной Y относительно теоретической линии дисперсии, определяющей влияние прочих факторов на величину Y. - дисперсия переменной Y относительно теоретической линии дисперсии, определяющей влияние прочих факторов на величину Y.
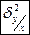 - условная дисперсия, характеризует дисперсию теоретической линии регрессии относительно условной генеральной средней my
. Именно она определяет влияние данного фактора (Х) на величину Y и может быть использована для оценки тесноты связи между величинами Х и Y. - условная дисперсия, характеризует дисперсию теоретической линии регрессии относительно условной генеральной средней my
. Именно она определяет влияние данного фактора (Х) на величину Y и может быть использована для оценки тесноты связи между величинами Х и Y.
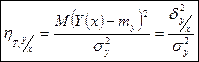 - теоретическое корреляционное отношение. - теоретическое корреляционное отношение.
Изменяется от 0 до 1, что легко доказать, поделив (*) на sу
2
:
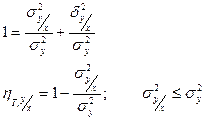
1) Если 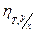 =1, то =1, то 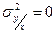
Влияние прочих факторов отсутствует. Все распределение будет сконцентрировано на линии регрессии. В этом случае между Х и Y существует простая функциональная зависимость.
2) Если 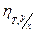 =0, когда =0, когда 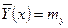 . .
В этом случае линия регрессии Y по Х будет горизонтальной прямой, проходящей через центр распределения.
В случае, когда вид зависимости (форма связи) случайных величин Х и Y не установлен, часто бывает необходимо убедиться в наличии какой-либо связи вообще. Может оказаться, что связь несущественна и вычисление коэффициентов регрессии неоправданно.
Для объяснения такого вопроса вычисляется эмпирическое корреляционное отношение, определяемое на основе выборочных данных. При выводе формул для ЭКО пользуются эмпирической линией регрессии и оценкой дисперсии по выборке.
Определение эмпирического корреляционного соотношения.
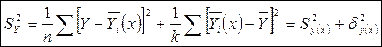
y – измеряемое значение зависимой переменной
n – общее количество измерений
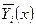 - условное среднее (среднее значение зависимой переменной у в i-ом интервале св Х) - условное среднее (среднее значение зависимой переменной у в i-ом интервале св Х)
k – общее количество интервалов
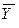 - среднее всей совокупности измерений - среднее всей совокупности измерений
В пределах каждого интервала, для всех тех значений Х, для которых есть экспериментальные результаты (значения Y), находим средние значения.
 Sy(x)
2
– составляющая полной дисперсии, характеризует дисперсию результатов измерений относительно эмпирической линии регрессии, т.е. влияние прочих факторов на зависимую переменную Y. Sy(x)
2
– составляющая полной дисперсии, характеризует дисперсию результатов измерений относительно эмпирической линии регрессии, т.е. влияние прочих факторов на зависимую переменную Y.
dy
(
x
)
2
– характеризует дисперсию эмпирической линии регрессии относительно среднего всей совокупности, т.е. влияние исследуемого фактора на зависимую переменную Y.
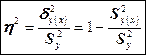 - Эмпирическое корреляционное соотношение - Эмпирическое корреляционное соотношение
Из сравнения с формулой для теоретического корреляционного соотношения видно: при расчете теоретического корреляционного соотношения
необходимо знать форму связи между переменными.
При вычислении эмпирического корреляционного соотношения никакие предположения о форме связи не используются, нужна только эмпирическая линия регрессии.
Свойства:
1. 0 £ £ 1 £ 1
2. если  =1, все точки корреляционного поля лежат на линии регрессии – функциональная связь между Х и Y. =1, все точки корреляционного поля лежат на линии регрессии – функциональная связь между Х и Y.
3. Если  =0 (когда =0 (когда  ), отсутствует изменчивость условных средних ), отсутствует изменчивость условных средних 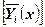 , эмпирическая линия регрессии проходит параллельно оси абсцисс – свзи между Х и Y нет. , эмпирическая линия регрессии проходит параллельно оси абсцисс – свзи между Х и Y нет.
Эмпирическое корреляционное соотношение  завышает тесноту связи между переменными и случайными величинами, причем тем сильнее, чем меньше число измерений, поэтому завышает тесноту связи между переменными и случайными величинами, причем тем сильнее, чем меньше число измерений, поэтому  рекомендуется использовать для предварительной оценки тесноты связи, а для окончательной оценки – теоретическое корреляционное соотношение. рекомендуется использовать для предварительной оценки тесноты связи, а для окончательной оценки – теоретическое корреляционное соотношение.
Коэфициент корреляции.
Рассмотрим случай вычисления теоретического корреляционного соотношения 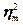 , когда связь между случайными величинами Х и Y является линейной. , когда связь между случайными величинами Х и Y является линейной.
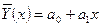
Такая форма связи между Х и Y имеет место в случае, когда случайные величины подчиняются двуменому нормальному закону распределения.
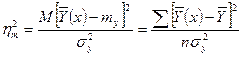
Подставив вместо Y и 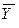 их значения для случая линейной зависимости: их значения для случая линейной зависимости:
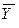 = =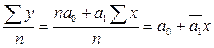
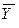 (х)=а0
+ а1
х (х)=а0
+ а1
х
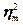 = =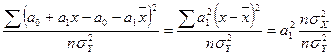
Заменим а1
ее значением, полученным из решения нормальных уравнений:
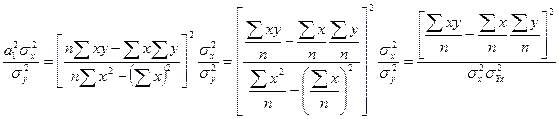
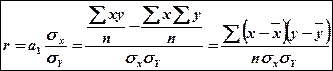
Коэфициент корреляции является частным случаем теоретического корреляционного соотношения 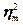 , когда связь между СВ является линейной. В этом случае r является показателем тесноты связи. , когда связь между СВ является линейной. В этом случае r является показателем тесноты связи.
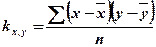 - выборочный корреляционный момент - выборочный корреляционный момент
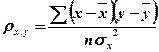 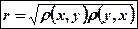
Выборочный коэфициент корреляции обладает свойствами:
1. r=0, если св Х и Y независимы
2. 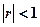 - Для любых св Х и Y - Для любых св Х и Y
3. 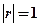 - Для случая линейной зависимости св Х и Y. - Для случая линейной зависимости св Х и Y. 
Коэфициент корреляции используется для оценки тесноты связи и в случае нелинейной зависимости между случайными величинами.
Если предварительный графический анализ поля корреляции указывает на какую либо тесноту связи, полезно вычислить коэфициент корреляции.
Если модуль коэфициента корреляции 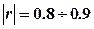 , то независимо от вида связи можно считать, что она достаточно тесна, чтобы исследоват ее форму. , то независимо от вида связи можно считать, что она достаточно тесна, чтобы исследоват ее форму.
Двумерное нормальное распределение.
Его возникновение объясняется центральной предельной теоремой Ляпунова:
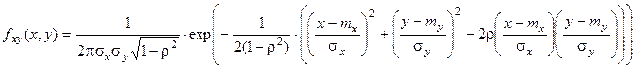
r – коэффициент корреляции. Х и У по отдельности распределены нормально (mx
,sx
) и (my
,sy
).
В частном случае независимых СВ Х и У r=0:
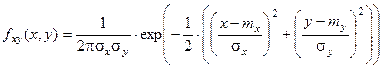
Исходные плотности одномерных нормальных распределений Х и У:
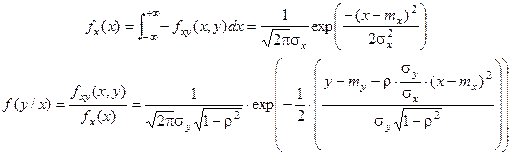
Условное распределение
– нормальное с условиями:
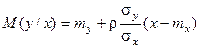 и и 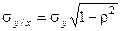 . .
Первое условие является уравнением функции регрессии.
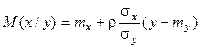 и и 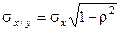 . .
Нормальная регрессия прямолинейна. Точность оценки у/х одинакова для всех х. В качестве меры тесноты связи используется коэффициент корреляции, а форму связи при этом характеризует коэффициент регрессии.
Z=fxy
(x,y) – трехмерная поверхность, сечения которой плоскостями XZ и YZпредставляют собой графики плотности одномерных распределений.
Коэффициент множественной корреляции

D* – это в с добавочными верхней строкой и правым столбцом, состоящих из свободных членов уравнений.
Пример
: Вычислить КМК:
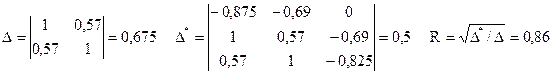
Коэффициент корреляции рангов (объединенные ранги)
Анализ информации неподдающейся количественной оценке.
На экзаменах разные экзаменаторы ставят одним и тем же студентам разные оценки. Чтобы исключить элемент субъективизма, всех учащихся располагают в соответствии со степенью их способностей и ранжируют. Корреляция между рангами значительно точнее отражает взаимосвязь.
Есть n учащихся и ранги по некоторому фактору А: X1
…Xn
и по фактору B: Y1
…Yn
.
Xi
, Yi
– перестановки n первых натуральных чисел.
Xk
-Yk
=dk
– мера тесноты связи A и B. Если все dk
=0, то A и B полностью соответствуют.
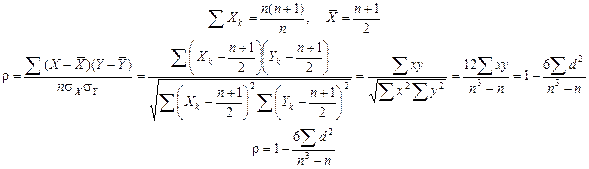
Последнее выражение – коэффициент корреляции рангов Спирмена
.
Существуют и другие показатели тесноты связи:
ККР Кендела
: удобен для углубленных исследований, когда невозможно установит ранговые различия. Строятся объединенные усредненные ранги и
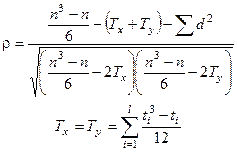
ti
– число объединенных рангов.
Метод ранговой корреляции
Позволяет анализировать множество факторов и выделять доминирующие.
Для построения математической модели процесса необходимо выделить из множества факторов доминирующие. На первом этапе это делается с помощью экспертных оценок: максимальному кругу специалистов предлагается расположить факторы в порядке убывания степени влияния. При этом предлагается максимально полный список факторов, хотя каждый может включать в этот список дополнительные факторы.
Результат – матрица рангов, которая строится с учетом квалификации опрашиваемого: показания специалистов умножаются на коэффициент квалификации. Чем меньше сумма рангов фактора, тем более важное место он занимает, тем большее влияние он оказывает на выходной параметр.
Если распределение на диаграмме близко к равномерному, то все факторы должны учитываться. Обычно отмечается, что опрос не дал желаемого результата.
Если не равномерно, но изменение рангов не велико, значит специалисты делают различия между факторами, но неуверенно. Таким образом, надо учитывать все факторы.
Наиболее благоприятен случай быстрого экспоненциального спада суммы рангов. Малозначащие факторы отсеиваются. Для оценки степени согласованности мнений специалистов вычисляется коэффициент конкордации
:
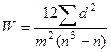
m – число специалистов
n – число факторов.
Чем больше W, тем больше степень согласованности. Если W=0, то согласованность отсутствует. При W=1 – полная согласованность.
Планирование эксперимента
Классический регрессионный и корреляционный анализ базируются на пассивном эксперименте, который сводится к сбору и обработке данных, полученных в результате наблюдения за процессом или явлением.
Привлекательность пассивного эксперимента в том, что он избавляет от необходимости тратить время и средства на постановку опытов. Полученные результаты в виде уравнения регрессии можно затем использовать для управления процессом. Однако пассивный эксперимент имеет ряд недостатков:
1. При сборе экспериментальных данных на реальном действующем промышленном объекте во избежание появления брака возможны лишь незначительные изменения параметров процесса. При этом интервалы варьирования параметров оказываются столь малыми, что изменение выходной величины будет в значительной степени обусловлено воздействием случайных факторов.
2. Часто упускают из вида важные факторы из-за невозможности их измерения или регистрации.
3. При пассивном эксперименте нельзя произвольно варьировать параметры. В результате этого экспериментальные точки часто располагаются неудачно и при большом количестве опытов затрудняют точное описание процесса.
Активный эксперимент
Ставится по плану. Достоинства:
1. Появляется четкая логическая схема всего исследования.
2. Повышается эффективность исследования. Оказывается возможным извлечь максимальное количество информации.
3. Обработка результатов эксперимента осуществляется стандартными приемами.
4. Планирование эксперимента позволяет обеспечить случайный порядок проведения опытов (рандомизация).
Отпадает необходимость в жесткой стабилизации мешающих факторов.
Активный эксперимент эффективен в лабораторной практике, а пассивный – в производстве.
С помощью методов планирования эксперимента можно получить математическую модель изучаемого процесса в аналитическом виде при отсутствии сведений о механизме процесса.
Математическая модель процесса задается полиномом:
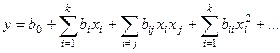
Чаще всего используется линейная модель:
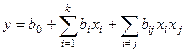
План эксперимента определяет расположение точек в к-мерном факторном пространстве.
Матрица планирования
: каждая строчка – условие проведения опыта, а столбец – значения переменной в различных опытах.
При выборе линейной модели достаточно варьировать каждый фактор на двух уровнях. Если при этом осуществляются все возможные комбинации из k факторов, то реализация эксперимента по такому плану называется полным факторным экспериментом типа 2k
(ПФЭ 2k
).
Построение математической модели методом ПФЭ проводится в следующем порядке:
1. Планирование эксперимента
2. Проведение эксперимента
3. Проверка воспроизводимости
4. Построение математической модели с проверкой статистической значимости всех коэффициентов
5. Проверка адекватности математической модели.
Центр плана (точка, вокруг которой ставится серия опытов) выбирается на основании априорных сведений о процессе.
Если эти сведения отсутствуют, то в качестве центра плана выбирается центр исследуемой области.
|