| Федеральное Агентство по образованию
государственное Образовательное Учреждение высшего профессионального образования
«
Тюменский Государственный Нефтегазовый Университет»
Институт Нефти и Газа
Кафедра «
математические методы в экономике»
Курсовая работа
по математическому анализу
Однородные и неоднородные системы линейных дифференциальных уравнений
Проверил: старший преподаватель
Тюмень 2007
Содержание
ВВедение
1 Системы линейных дифференциальных уравнений.
1.1 Общие сведения о линейных системах.
1.2 Метод сведения линейной системы к одному уравнению более высокого порядка.
1.3 Методы решения однородных линейных систем дифференциальных уравнений.
1.4 Методы решения неоднородных линейных систем дифференциальных уравнений.
2. Решение линейных систем дифференциальных уравнений.
2.1.Решение методом сведения линейной системы к одному уравнению более высокого порядка.
2.2. Решение однородных линейных систем дифференциальных уравнений.
2.2.1. Решение видоизмененным методом Эйлера
2.3.2. Решение методом неопределенных коэффициентов
ВВЕдение
1. Системы линейных дифференциальных уравнений.
1.1 Общие сведения о линейных системах.
Линейные системы – это системы дифференциальных уравнений вида
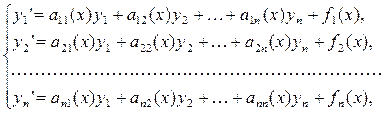 (1) (1)
Где коэффициенты aij
и fi
– некоторые функции независимой переменной x
. Будем считать их непрерывными; тогда для данной системы заведомо выполняются условия теоремы о существование и единственности решения задачи Коши. Если все fi
=0, то система называется однородной
, в противном случае она называется неоднородной.
Система
 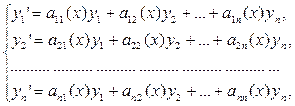 (2) (2)
Называется однородной системой
, соответствующей неоднородной системе
(1).
При изучении линейных систем удобно использовать матричные обозначения
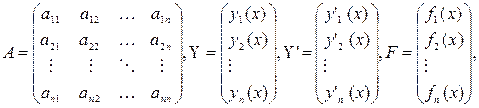
Позволяющие записать систему (1) в виде одного матричного уравнения
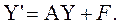 (3) (3)
Так же, как и в случае линейных уравнений, общее решение неоднородной системы представляет собой сумму частного решения этой системы и общего решения соответствующей ей однородной системы. В свою очередь, общее решение однородной системы имеет вид
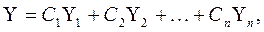 (4) (4)
Где С1
,…,Сn
- произвольные постоянные, а
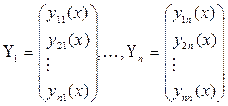
-произвольные линейно независимые решения, называемые фундаментальным набором решений
этой системы. Критерием линейной независимости этих решений является неравенство нулю определителя Вронского
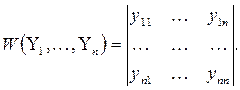 (5) (5)
1.2 Метод сведения линейной системы к одному уравнению более высокого
порядка.
(Этот метод применим как для однородной, так и для неоднородной системы линейных дифференциальных уравнений.)
Один из методов интегрирования линейной системы заключается в сведении системы к одному уравнению n-ого порядка с одной неизвестной функцией. Продемонстрируем это на примере системы двух уравнений.
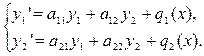 (6) (6)
Дифференцируя (по x) обе части первого уравнения системы (6), находим
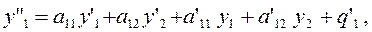
откуда, заменяя производные y1
', y2
' их выражениями из самой системы, имеем
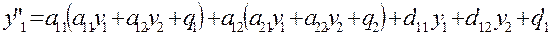 . .
Группируя в правой части, получим уравнение вида
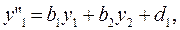 (7) (7)
Где коэффициенты b1
, b2
и d1
определенным образом выражаются через коэффициенты aij
и q
1
и их производные. Комбинируя уравнение (7) с первым уравнением системы (6), получим
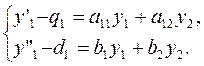 (8) (8)
Предположим, что в рассматриваемой области изменения x определитель
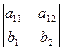  отличен от нуля. Тогда систему (8) можно решить относительно y1
и y2
, т.е. выразить y1
и y2
через y’1
и y”2
. отличен от нуля. Тогда систему (8) можно решить относительно y1
и y2
, т.е. выразить y1
и y2
через y’1
и y”2
.
В результате приходим к уравнениям вида
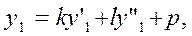 (9) (9)
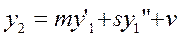 . (10) . (10)
Первое из них представляет собой линейное дифференциальное уравнение второго порядка с одной неизвестной функцией y1
(t). Заметим, что если в исходной системе (6) все коэффициенты aij
постоянны, то уравнение (9) также является уравнением с постоянными коэффициентами. [ 3 стр 509-510]
1.3 Методы решения однородных линейных систем дифференциальных уравнений.
1) Сведение к одному уравнению n-ого порядка. (Этот метод мы разбирали выше)
2) Решение ЛОСДУ с постоянными коэффициентами с помощью матриц (видоизмененный метод Эйлера).
Пусть дана система n линейных дифференциальных уравнений с n неизвестными функциями, коэффициенты которой постоянные:
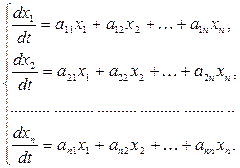 (11) (11)
Эту систему можно записать в виде одного матричного дифференциального уравнения
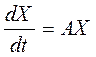 . .
Здесь
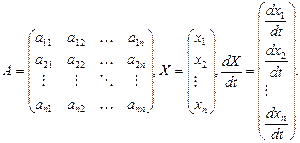
[2 стр 169]
Ищем решение системы в виде:
X1
=α1
ekt
, X2
=α2
ekt
,……. Xn
=αn
ekt
. (12)
Требуется определить постоянные α1,
α2
,…, αn
и k так, чтобы функции α1
ekt
, α2
ekt
,…,αn
ekt
удовлетворяли системе уравнений (11). Подставим их в систему(1), получим:
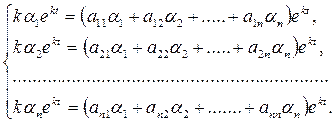
Сократим на ekt
. Перенося все члены в одну сторону и собирая коэффициенты при α1,
α2
,…., αn
, получим систему уравнений
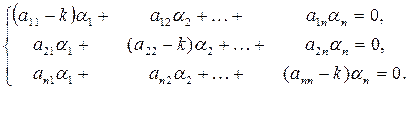 
Выберем α1,
α2
,…., αn
и k такими, чтобы удовлетворялась система (13).Эта система есть система линейных однородных алгебраических уравнений относительно α1,
α2
,…., αn
. Составим определитель системы (13):
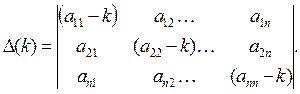 (14) (14)
Если k таково, что определитель ∆ отличен от нуля, то система (13) имеет только нулевые решения α1
=α2
=…=αn
=0,а следовательно, формулы (12) дают только тривиальные решения:
X1
(t)=X2
(t)=…=X(t)=0.
Таким образом, нетривиальные решения (12) мы получим только при таких k,при которых определитель (14) обращается в нуль. Мы приходим к уравнению n-ого порядка для определения k:
 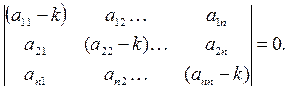 (15) (15)
Это уравнение называется характеристическим уравнением для системы (1),его корни называются корнями характеристического уравнения.
Рассмотрим несколько случаев.
Случай 1. Корни характеристического уравнения действительны и различны. Обозначим через k1
, k2
,….kn
корни характеристического уравнения. Для каждого корня kj
напишем систему (13) и определим коэффициенты
α1
(
i
)
,α2
(
i
)
,…, αn
(
i
)
.
Можно показать, что один из них произвольный, его можно считать равным единице. Таким образом, получаем:
для корня k1
решение системы (11)
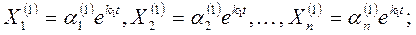
Для корня k2
решение системы (1)
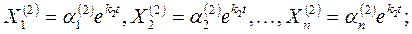
……………………………………………………….
для корней kn
решение системы (1)
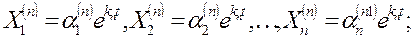
Путем непосредственной подстановки в уравнения можно убедиться, что система функций
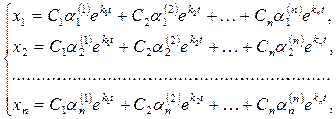 (16) (16)
где С1
, С2
,….,Сn
-произвольные постоянные, тоже является решением системы дифференциальных уравнений (11). Это есть общее решение системы (11). Легко показать, что можно найти такие значения постоянных, при которых решение будет удовлетворять заданным начальным условиям.
Случай 2. Корни характеристического уравнения различные, но среди них есть комплексные. Пусть среди корней характеристического уравнения имеется два комплексных сопряженных корня:
k1
= α+iβ, k2
= α-iβ.
Этим корням будут соответствовать решения

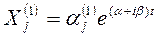 (j = 1, 2, …,n), (17) (j = 1, 2, …,n), (17)
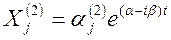 (j = 1, 2, …,n), (18)
(j = 1, 2, …,n), (18)
Коэффициенты α j
(
1
)
и α j
(2)
определяются из системы уравнений (13).
Можно показать, что действительные и мнимые части комплексного решения тоже являются решениями. Таким образом, мы получаем два частных решения:
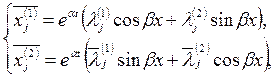 (19) (19)
Где 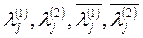 - действительные числа, определяемые через - действительные числа, определяемые через 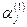 и и 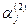 . Соответствующие комбинации функций (18) войдут в общее решение системы. [2 стр 112-115] . Соответствующие комбинации функций (18) войдут в общее решение системы. [2 стр 112-115]
Случай 3. Характеристическое уравнение имеет единственный корень k
(кратности 2), которому соответствуют два линейно независимых собственных вектора P1
и P2
(т.е. кратность корня совпадает с числом линейно независимых собственных векторов). Векторы P1
и P2
порождают два линейно независимых решения
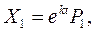 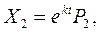
И общее решение, так же как и в случае 1, находится по формуле (4) .
Случай 4. Характеристическое уравнение имеет единственный корень k
(кратности 2), которому с точностью до постоянного множителя соответствует один собственный вектор P1
(т.е. кратность корня больше числа линейно независимых собственных векторов). В этом случае для отыскания решения целесообразно применить метод неопределенных коэффициентов
. Согласно этому методу общее решение необходимо искать в форме
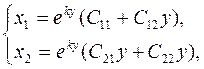
Где постоянные Сij
требуют определения путем подстановки этих выражений в исходную однородную систему.
Замечание. Для решения однородных систем в случае, когда корень характеристического уравнения λ кратный и ему соответствует единственный собственный вектор P1
, может быть применен метод присоединения векторов
.
Суть его такова. Пусть P2
– вектор-столбец, являющийся решением уравнения
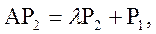 (20) (20)
тогда однородная система
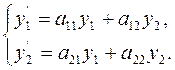 (21) (21)
имеет два линейно независимых решения
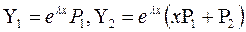 . .
Покажем, что Y2
является решением. Имеем
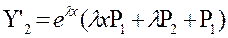 . .
Учитывая, что P1
и - собственный вектор, а P2
удовлетворяет условию (20), получаем
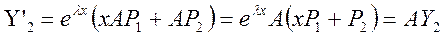 . .
Нетрудно также убедиться, что Y1
и Y2
линейно независимы. Следовательно, они образуют фундаментальный набор решений, и общее решение может быть найдено по формуле (4).
В общем случае корню характеристического уравнения λ кратности k>1, имеющему один собственный вектор P1
,соответствует k линейно независимых решений
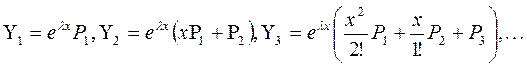
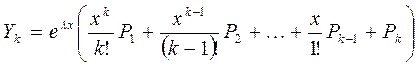 , (22) , (22)
Где присоединенные векторы P2
,P3
,…,Pk
являются последовательными решениями следующих алгебраических систем
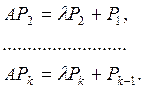 (23) [3 стр 519-522] (23) [3 стр 519-522]
1.4 Методы решения
неоднородных
линейных систем дифференциальных уравнений.
1) Для решения неоднородных линейных систем применяются методы, аналогичные методам, используемым для решения неоднородных линейных уравнений. Одним из таких методов является метод вариации постоянных.
Продемонстрируем его суть на следующем примере.
Пример: 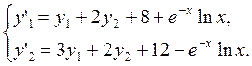
Решение. Решая характеристическое уравнение
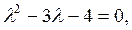
Находим корни λ1
=-1, λ2
=4. Собственными векторами, отвечающими найденным собственным значениям, будут соответственно
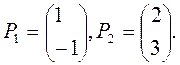
Следовательно, общее решение соответствующей однородной системы имеет вид
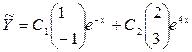 . .
Решение неоднородного уравнения в соответствии с методом вариации постоянной будем искать в форме
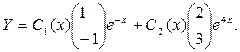
Для нахождения С1
(x) и C2
(x) подставив выражение для Y в исходную систему, получим
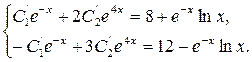
Отсюда находим:
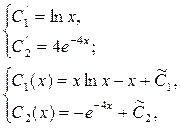
где 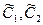 - производные постоянные. Таким образом, решение исходной системы будет - производные постоянные. Таким образом, решение исходной системы будет
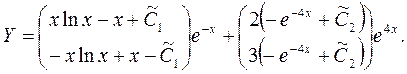
2) В случае, когда столбец свободных членов системы имеет специальный вид
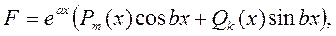 (24) (24)
Где Pm
(x) и Qk
(x) – вектор-столбцы, элементами которых являются многочлены от х степени, не превышающей соответственно n и k, для отыскания частного решения уравнения целесообразно воспользоваться методом неопределенных коэффициентов
. Для систем он имеет определенную специфику. Суть метода такова.
Если число γ =
a
+
bi
не является корнем характеристического уравнения, то частное решение ищется в виде
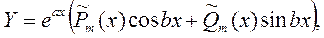
где 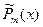 и и 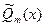  - вектор-столбцы, элементами которых являются многочлены от x степени m=max{k,n}. - вектор-столбцы, элементами которых являются многочлены от x степени m=max{k,n}.
Если же  γ является корнем характеристического уравнения кратности l
(резонансный случай), то частное решение ищется в форме γ является корнем характеристического уравнения кратности l
(резонансный случай), то частное решение ищется в форме
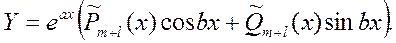 [ 3 стр 529-531] [ 3 стр 529-531]
2. Решение линейных систем дифференциальных уравнений.
2.1.Решение методом сведения линейной системы к одному уравнению более высокого порядка.
2.2. решение однородных линейных систем дифференциальных уравнений.
2.2.1. Решение
видоизмененным методом Эйлера
Случай 1
Пример1. 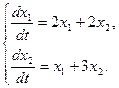
Решение. Составляем характеристическое уравнение
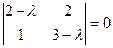
Или 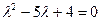 . Находим корни: . Находим корни:
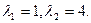
Решение системы ищем в виде
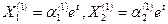
и
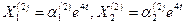 . .
Составим систему (3) для корня 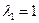 и определяем и определяем 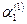 и и 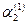 : :
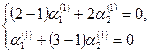
Или
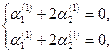
Откуда 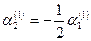 . Полагая . Полагая 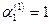 , получаем , получаем 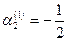 . Таким образом, мы получили решение системы: . Таким образом, мы получили решение системы:
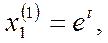 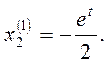
Составим далее систему (3) для корня 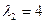 и определяем и определяем 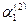 и и 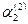 : :
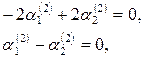
Откуда 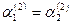 и и 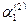 =1, =1, 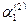 =1. Получаем второе решение системы: =1. Получаем второе решение системы:
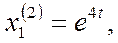 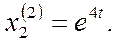
Общее решение системы будет (см (6))

Пример2. 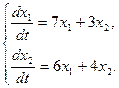
Решение. Составим характеристическое уравнение матрицы системы
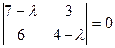 или или 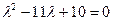
Находим его корни: 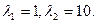
Составим систему (3) для корня 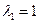 и определяем и определяем 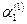 и и 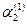 : :
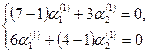 или или  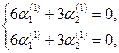 => => 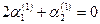
Откуда 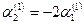 . Полагая . Полагая 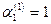 , получаем , получаем 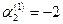 . .
Таким образом, мы получили решение системы:
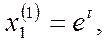 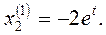
Составим далее систему (3) для корня 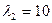 и определяем и определяем 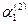 и и 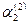 : :
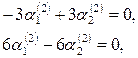
Откуда 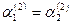 и и 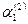 =1, =1, 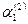 =1. =1.
Получаем второе решение системы:
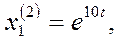 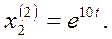
Общее решение системы будет
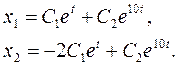
Пример3. 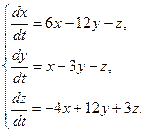
Решение. Составим характеристическое уравнение матрицы системы
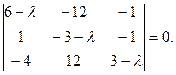
Раскрывая определитель, находим
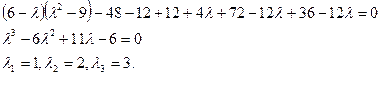
Составим систему (3) для корня 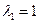
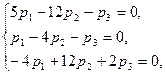
одно из которых - следствие двух других. Возьмем, например, первые два уравнения:
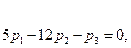 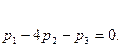
Отсюда
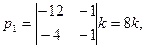 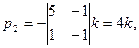 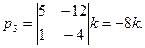
Приняв k=1/4,получаем собственный вектор (2;1;-2).
При λ=2 имеет систему
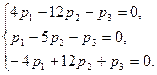
Используя первые два уравнения (третье – их следствие), находим
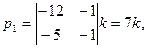 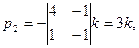 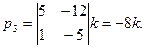
Полагая k=1, находим собственный вектор (7;3;-8).
При λ=3 имеет систему
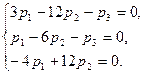
Из последнего уравнения находим 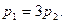 Подставляем это значение p1
в первое уравнение и находим Подставляем это значение p1
в первое уравнение и находим 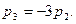 Приняв Приняв 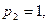 получаем получаем 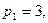 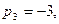 т.е. собственный вектор (3; 1; -3). т.е. собственный вектор (3; 1; -3).
Фундаментальная система решении:
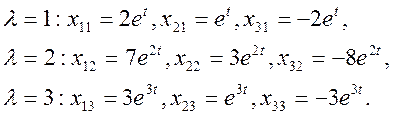
Общее решение записываем в виде
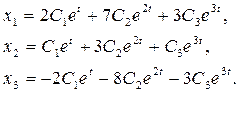
Случай 2.
Пример 1. 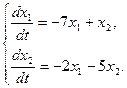
Решение. Составляем характеристическое уравнение
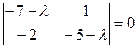 или или 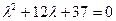
и находим его корни: 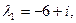 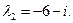
Подставляем 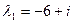 в систему (3) и определяем в систему (3) и определяем 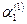 и и 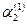 : :
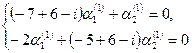 или или 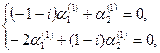
Откуда 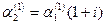 . Полагая . Полагая 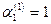 , получаем , получаем 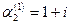 . .
Пишем решение (7):
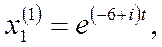 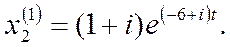
Подставляя 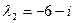 в систему (3), находим: в систему (3), находим:
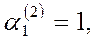 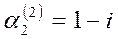 . .
Получим вторую систему решений (8):
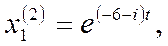 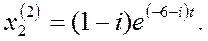
Перепишем решения:
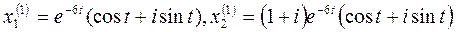
или
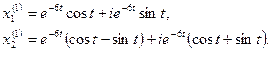
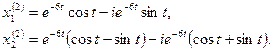
За системы частных решений можно взять отдельно действительные части и отдельно мнимые части
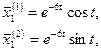 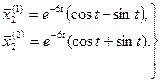
Общим решением системы будет
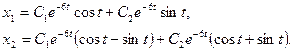
Пример 2. 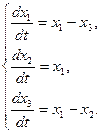
Решение. Составляем характеристическое уравнение
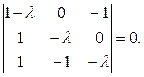 или или 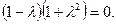
Характеристические числа: λ1
=1, λ2
=i, λ3
= - i.
При λ1
=1 для определения собственного вектора получаем систему уравнений
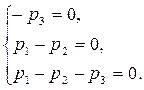
Эта система определяет собственный вектор (1; 1; 0).
При λ2
=i получаем систему уравнений
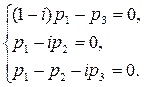
Эта система определяет собственный вектор (1; i; 1-i).
При λ3
= - i получаем систему уравнений
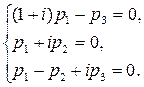
Эта система определяет собственный вектор (1; -i; 1+i).
Значению λ1
=1 соответствуют решения
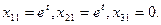
Значению λ2
=i соответствуют решения
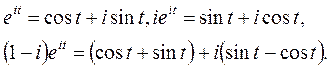
Значению λ3
= - i соответствуют решения
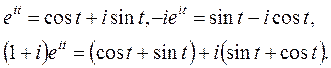
Отделяя действительные части, получим решения
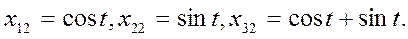 до решать до решать
Случай 4.
Пример 1. 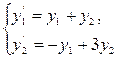
Решение. Характеристическое уравнение
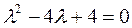
Имеет единственный корень λ=2 (кратности 2). Ему соответствует единственный собственный вектор
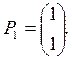
Поэтому решение в этом случае будем искать в виде
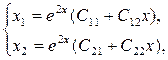
Подставляя выражения для y1
и y2
в исходную систему, находим
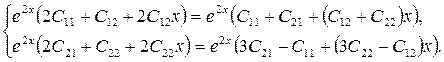
Отсюда получаем систему
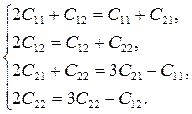
Решая её, находим
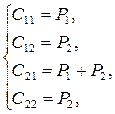
Где P1
, P2
– произвольные постоянные. Таким образом, общее решение системы имеет вид
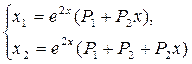
Пример 2. 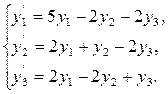
Решение. Составим характеристическое уравнение системы
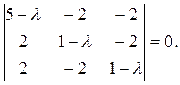
Раскрывая определитель, получаем
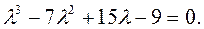
Данное уравнение после несложных преобразовании принимает вид
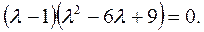
Отсюда находим: 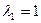 (простой корень), ему соответствует собственный вектор (простой корень), ему соответствует собственный вектор

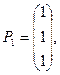
и 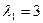 (корень кратности 2), которому соответствуют два линейно независимых собственных вектора (корень кратности 2), которому соответствуют два линейно независимых собственных вектора
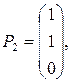 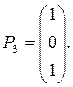
Следовательно, общее решение системы имеет вид
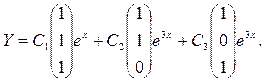
2.3. решение неоднородных линейных систем дифференциальных уравнений.
2.3.1. Решение методом вариации постоянных.
Пример 1.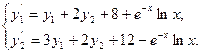
Решение. Решая характеристическое уравнение
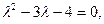
Находим корни 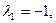 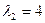 . Собственными векторами, отвечающими найденным собственным значениям, будут соответственно . Собственными векторами, отвечающими найденным собственным значениям, будут соответственно
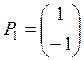 , , 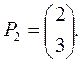
Следовательно, общее решение соответствующей однородной системы имеет вид
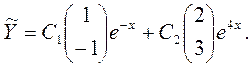
Решение неоднородного уравнения в соответствии с методом вариации постоянной будем искать в форме
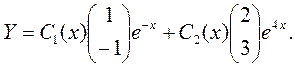
Для нахождения С1
(x) и С2
(x) подставив выражение для Y в исходную систему, получим
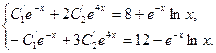
Отсюда находим:
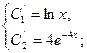
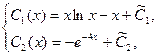
Где 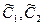 - произвольные постоянные. Таким образом, решение исходной системы будет - произвольные постоянные. Таким образом, решение исходной системы будет
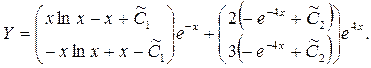
2.3.2.
Решение методом неопределенных коэффициентов
Пример 1. 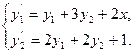
Решение. Решая характеристическое уравнение системы
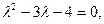
Находим корни 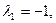 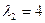 . Собственными векторами, отвечающими найденным собственным значениям, будут соответственно . Собственными векторами, отвечающими найденным собственным значениям, будут соответственно
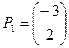 , , 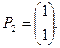
Следовательно, общее решение соответствующей однородной системы имеет вид
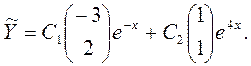
Теперь найдем частное решение. В рассматриваемом случае элементы столбца свободных членов представляют собой многочлены степени, не превышающей 1, и так как число γ=0 не совпадает с корнями характеристического уравнения, то частное решение неоднородной системы будем искать в виде
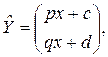
Где p, q, c и в – некоторые постоянные. Для их определения подставим выражение для 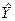 в исходную систему. Получим в исходную систему. Получим
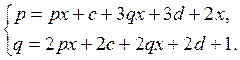
Отсюда
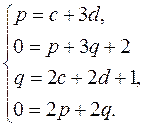
Решив эту систему, находим p=1, q= - 1, c= - 2 и d=1. Следовательно,
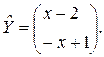
Так как общее решение неоднородной системы уравнения Y представляет собой сумму частного решения 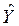 и общего решения и общего решения 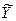 соответствующей однородной системы, то окончательно получаем соответствующей однородной системы, то окончательно получаем
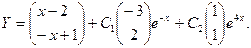
Пример 2. 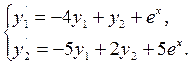
Решение. Решая характеристическое уравнение системы
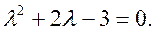
Его корни будут 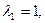 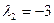 . Им соответствуют собственные векторы . Им соответствуют собственные векторы
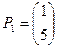 , , 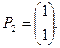
Следовательно, общее решение соответствующей однородной системы имеет вид
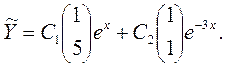
Теперь найдем частное решение. В рассматриваемом случае число γ= 1 совпадает с корнем λ1
характеристического уравнения (резонансный случай). Так как элементы столбца свободных членов представляют собой многочлены нулевой степени, частное решение неоднородной системы будем искать в виде
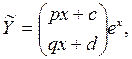
где p, q, c и в – некоторые постоянные. Подставим выражение для 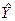 в исходную систему. Получим в исходную систему. Получим
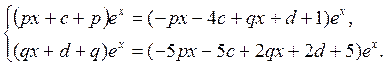
Отсюда
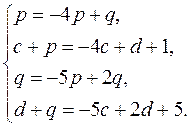
Решив эту систему, находим
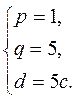
Полагая с =1, получаем в = 5. Следовательно,
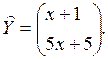
Таким образом, общее решение системы имеет вид
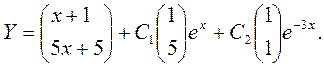
Список используемой литературы
1. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Выцсшая математика в упражнениях и задачах. –М.: “Высшая школа”, 1986.
2. Пискунов Н.С. Дифференциальное и интегральное исчисления.- М.:”Наука”, 1978.
3. Солодовников А.С., Бабайцев В.А., Браилов А.В., Шандра И.Г. Математика в экономике.- М.:”Финансы и статистика”, 2003.




|