|
Государственное образовательное учреждение
среднего профессионального образования
Волгодонский педагогический колледж
Допущена к защите
“____”____________200__г. Защищена с отметкой:______
Зам. директора по управлению Протокол ИГА №__________
образовательным процессом ________________________
________________________
Выпускная квалификационная работа
Тема:
«Алгебраические уравнения с одной неизвестной и способы их решения в основной школе»
Специальность: 050201_Математика
Выполнил(а):
студент(ка)
Руководитель:
Волгодонск 2007 г.
СОДЕРЖАНИЕ
Введение……………………………………………………………………......3
ГЛАВА I. Теоретические особенности алгебраических уравнений.
§1. Уравнения с одним неизвестным. Корень уравнения…………...6
§2. Линейные уравнения………………………………………………....10
§3. Квадратные уравнения. Теорема Виета (прямая и обратная)…….......13
§4. Разложение квадратного трехчлена на множители……………….......21
§5. Уравнения, приводимые к линейным и квадратным………………23
§6. Уравнения третей степени…………………………………………...26
§7. Уравнения четвертой степени……………………………………….29
§8. Уравнения, содержащие неизвестное под знаком абсолютной
величины………………………………………………………………32
ГЛАВА II. Использование способов решения алгебраических уравнений на педагогической практике.
§1. Задачи, условия и этапы организации экспериментальной работы по
внедрению алгебраических уравнений на уроках математики в 8 классах…………………………………………………………….34
§2. Эффективность использования разработанной системы………......41
Заключение…………………………………………………………………........43
Список литературы………………………………………………………….......44
Приложения……………………………………………………………………...46
Введение
Велика роль математики в современном мире. Она занимает почетное место в сложном и бурном процессе развития человеческого общества и сама становится производительной силой. Практика наших дней оказывается богатейшим источником новых типов математических задач. Все эти задачи не только выдвинули физические, инженерные и технологические проблемы, но и привели к созданию новых разделов математики, таких как программирование для ЭВМ, ветвящиеся случайные процессы, теория оптимального уравнения и многие другие.
Сегодня понятие «алгебраические уравнения» стало необходимым элементом общей математической культуры. При этом учащиеся должны не только знать основные определения данного материала, но и осознавать необходимость глубокого изучения алгебраических уравнений, их решений. Изучение уравнений способствует расширению кругозора учащихся, улучшению качества их знаний и помогает при поступлении в ВУЗы. Поэтому актуальностью исследования
является изучение и решение алгебраических уравнений.
Рассмотрение этого вопроса в научно-методической литературе не решает проблемы по изучению данного материала в школьном курсе математики. Во-первых, не выделяется достаточно времени на более глубокое изучение исследуемых понятий; во-вторых, программой не предусмотрен достаточно подробный разбор уравнений, их решений в основной общеобразовательной школе, которые содействуют развитию математического мышления, формированию научного мировоззрения.
На современном этапе развития общества к математике предъявляются серьезные требования с технологизацией и информатизацией.
Поэтому проблему
нашего исследования мы видим в необходимости систематизации и углубления знаний учащихся по данному материалу и отсутствии системности при изучении этого материала в курсе основной школы, что не позволяет сделать процесс обучения оптимальным.
Объект исследования:
процесс обучения математики в основной общеобразовательной школе.
Предмет исследования:
алгебраические уравнения и способы их решения как составляющая курса обучения математики.
Цель исследования:
изучить в теории и практике способы решения алгебраических уравнений с одним неизвестным, выявить методические условия, способствующие повышению знаний, умений и навыков учащихся по решению различных видов алгебраических уравнений и апробировать их на практике.
Исходя из поставленных целей исследования, вытекают следующие задачи:
1. Выявить различные виды и способы решения алгебраических уравнений с одним неизвестным.
2. Определить методологические условия, способствующие качественному формированию знаний, умений и навыков в решении алгебраических уравнений.
3. Апробировать на практике в основной школе различные способы решения алгебраических уравнений.
Гипотеза:
системное изложение учебного материала по алгебраическим уравнениям в курсе основной общеобразовательной школы будет способствовать углублению и оптимизации знаний по математике и созданию прочной базы для усвоения курса высшей математики.
Методологической основой нашего исследования
явилась гуманистическая личностно-ориентированная концепция обучения, которая позволяет поставить потребности учащихся в центре всей педагогической системы.
Теоретическая значимость:
на основе теоретического обобщения научно-методических источников выявлен наиболее оптимальный способ решения алгебраических уравнений с одним неизвестным.
Методы исследования:
анализ научно-методической литературы по проблеме исследования, методы эмпирического исследования: наблюдение, анкетирование, контрольные задания, экспериментальные методы статистической обработки результатов.
База исследования
: теоретические разработки исследования апробировались в 8 классе средней общеобразовательной школы №4 Мартыновского района, хутора Малоорловский.
ГЛАВА
I
. Теоретические особенности алгебраических уравнений.
§1. Уравнения с одним неизвестным. Корень уравнения.
Буквенные величины, входящие в равенство двух выражений 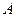 и и 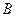 : : 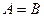 , по условию задачи могут быть неравноправными. Одни из них считаются известными, или параметрами. Они могут принимать все свои допустимые значения. Другие буквенные величины являются неизвестными. , по условию задачи могут быть неравноправными. Одни из них считаются известными, или параметрами. Они могут принимать все свои допустимые значения. Другие буквенные величины являются неизвестными.
Равенство, содержащее неизвестные числа, обозначенные буквами, называется уравнением.
В зависимости от числа неизвестных, входящих в уравнение, рассматривают уравнения с одним, с двумя и т.д. неизвестными.
Неизвестные величины в уравнениях обычно обозначают буквами 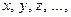 а известные (или параметры) – буквами а известные (или параметры) – буквами 
Будем сначала рассматривать уравнение с одним неизвестным 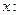
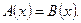
Выражения, стоящие слева и справа от знака равенства, называются левой и правой частями уравнения. Каждое слагаемое части уравнения называется членом уравнения.
Областью допустимых значений (сокращенно ОДЗ) или областью определения уравнения 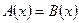 называется множество всех числовых значений неизвестного называется множество всех числовых значений неизвестного 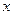 , при каждом из которых имеют смысл выражения , при каждом из которых имеют смысл выражения 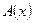 и и 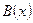 одновременно. одновременно.
Определение.
Корнем (или решением) уравнения называется то значение неизвестного, при котором это уравнение обращается в верное равенство. [20, c.34]
Очевидно, что корень уравнения принадлежит ОДЗ этого уравнения.
Решить уравнение - это значит найти все его корни или установить, что их нет.
Например, уравнение 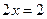 имеет единственный корень имеет единственный корень  ; уравнение ; уравнение 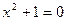 не имеет корней во множестве R: для любого действительного числа не имеет корней во множестве R: для любого действительного числа 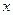 всегда всегда 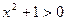 . .
Определение.
Два уравнения называются равносильными (эквивалентными), если всякий корень одного уравнения является корнем другого, и наоборот. Если оба уравнения не имеют корней (решений), то они также считаются равносильными. [20, c.34]
Иначе говоря, равносильными называются уравнения, множества корней которых совпадают.
Если уравнения 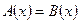 и и 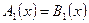 равносильны, то пишут равносильны, то пишут 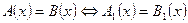 . .
Например, 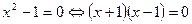 ; ; 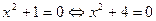 , так как эти уравнения не имеют действительных корней. Ясно, что уравнения , так как эти уравнения не имеют действительных корней. Ясно, что уравнения  и и 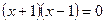 неравносильны. неравносильны.
При решении уравнения путем различных преобразований стараются заменить его более простым, равносильным ему уравнением. Однако такая замена не всегда удается. Тогда возможны следующие два случая:
1. При переходе к новому уравнению может произойти потеря корней. Например, при переходе от уравнения 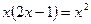 к уравнению к уравнению 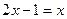 сокращением на неизвестное сокращением на неизвестное 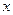 происходит потеря корня происходит потеря корня 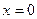 . Поэтому при переходе к новому уравнению надо учитывать возможность потери корня данного уравнения. . Поэтому при переходе к новому уравнению надо учитывать возможность потери корня данного уравнения.
2. Новое уравнение может содержать корни, не являющиеся корнями
данного уравнения (так называемые посторонние корни). Например, при переходе от уравнения 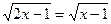 к уравнению к уравнению 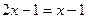 возведением в квадрат обеих частей исходного уравнения получим возведением в квадрат обеих частей исходного уравнения получим 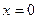 - посторонний корень этого уравнения. Поэтому часто делают проверку корней, подставив их в данное уравнение. - посторонний корень этого уравнения. Поэтому часто делают проверку корней, подставив их в данное уравнение.
Напомним, что числовые равенства обладают следующими свойствами:
1) числовое равенство не нарушится, если к обеим его частям прибавить
одно и то же число;
2) числовое равенство не нарушится, если обе его части умножить или
разделить на одно и то же число, отличное от нуля.
Из свойств числовых равенств и понятия равносильных уравнений вытекают следующие основные свойства уравнений:
1) Уравнение  , (1) равносильно уравнению , (1) равносильно уравнению 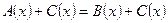 , (2) где , (2) где 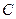 - число или некоторое выражение, имеющее смысл на множестве допустимых значений (т.е. на ОДЗ) уравнения - число или некоторое выражение, имеющее смысл на множестве допустимых значений (т.е. на ОДЗ) уравнения 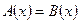 . .
Доказательство:
Обозначим через 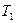 множество решений уравнения (1), а через множество решений уравнения (1), а через 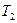 множество решений уравнения (2). Тогда уравнения (1) и (2) будут равносильны, если множество решений уравнения (2). Тогда уравнения (1) и (2) будут равносильны, если 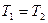 . Но чтобы убедиться в этом, необходимо показать, что любой корень из . Но чтобы убедиться в этом, необходимо показать, что любой корень из 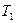 является корнем уравнения (2) и, наоборот, любой корень из является корнем уравнения (2) и, наоборот, любой корень из 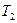 является корнем уравнения (1). является корнем уравнения (1).
Пусть число 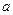 - корень уравнения (1). Тогда - корень уравнения (1). Тогда 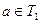 и при подстановке в уравнение (1) обращает его в истинное числовое равенство и при подстановке в уравнение (1) обращает его в истинное числовое равенство 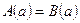 , а выражение , а выражение 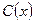 обращает в числовое выражение обращает в числовое выражение 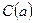 .
Прибавим к обеим частям истинного равенства .
Прибавим к обеим частям истинного равенства 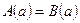 числовое выражение числовое выражение 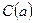 . Получим согласно свойствам истинных числовых равенств истинное числовое равенство . Получим согласно свойствам истинных числовых равенств истинное числовое равенство 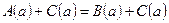 . .
Но это равенство говорит о том, что число 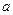 является также и корнем уравнения (2). является также и корнем уравнения (2).
Итак, доказано, что каждый корень уравнения (1) является корнем и уравнения (2), т.е. 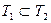 . .
Пусть теперь 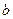 - корень уравнения (2). Тогда - корень уравнения (2). Тогда 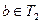 и при подстановке в уравнение обращает его в истинное числовое равенство и при подстановке в уравнение обращает его в истинное числовое равенство 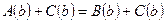 . .
Прибавим к обеим частям этого равенства числовое выражение 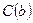 .
Получим истинное числовое равенство .
Получим истинное числовое равенство 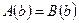 ,
которое говорит о том, что число ,
которое говорит о том, что число 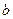 - корень уравнения (1). - корень уравнения (1).
Итак, доказано, что каждый корень уравнения (2) является и корнем уравнения (1), т.е. 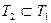 . .
Так как 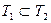 и и 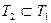 , то по определению равных множеств , то по определению равных множеств 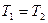 , а значит, уравнения (1) и (2) равносильны, ч.т.д. , а значит, уравнения (1) и (2) равносильны, ч.т.д.
Следствие. Любое слагаемое можно перенести из одной части уравнения в другую с противоположным знаком.
Например, 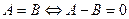 . .
2) Уравнение 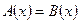 равносильно уравнению равносильно уравнению 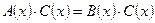 , где , где 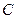 - число или некоторое выражение, имеющее смысл на множестве допустимых значений уравнения - число или некоторое выражение, имеющее смысл на множестве допустимых значений уравнения 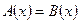 и не обращающееся на нем в нуль. и не обращающееся на нем в нуль.
Доказательство этого свойства аналогично доказательству свойства 1.
Следствие. Обе части уравнения можно сокращать на общий множитель, не обращающийся в нуль на множестве допустимых значений
данного уравнения.
Действительно, уравнение 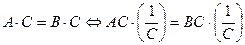 , т.е. , т.е.
равносильно уравнению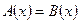 . .
3) Уравнение 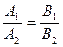 равносильно уравнению равносильно уравнению 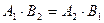 , рассматриваемому на множестве допустимых значений исходного уравнения , рассматриваемому на множестве допустимых значений исходного уравнения 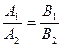 или на своем множестве при дополнительном условии или на своем множестве при дополнительном условии 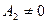 , , 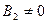 . .
Эти свойства используются при решении уравнений. [5, c.116]
§2.
Линейные уравнения.
Определение.
Уравнением первой степени с одним неизвестным называется уравнение вида 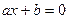 , где , где 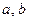 - заданные числа, причем - заданные числа, причем 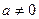 , а , а 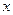 - неизвестное. - неизвестное.
При этом число 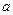 называется коэффициентом при неизвестном называется коэффициентом при неизвестном 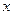 , ,
число 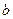 - свободным членом уравнения. - свободным членом уравнения.
Это уравнение равносильно уравнению  , из которого получаем, что , из которого получаем, что 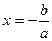 . Таким образом, уравнение первой степени всегда имеет единственный корень . Таким образом, уравнение первой степени всегда имеет единственный корень 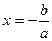 . .
Уравнение первой степени является частным случаем линейного уравнения  , где , где  - заданные числа, а - заданные числа, а 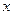 - неизвестное. - неизвестное.
Линейное уравнение сводится к равносильному ему уравнению вида 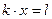 , где , где 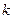 и и 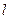 - известные числа. При этом число - известные числа. При этом число 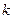 - коэффициент при неизвестном - коэффициент при неизвестном 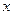 , может оказаться равным нулю, в отличие от коэффициента при неизвестном в уравнении первой степени. , может оказаться равным нулю, в отличие от коэффициента при неизвестном в уравнении первой степени.
Может оказаться, что линейное уравнение не имеет корней или имеет бесконечное множество корней. [5, с.118]
Пример 1.
Показать, что уравнение  не имеет корней. не имеет корней.
Решение. Данное уравнение равносильно уравнению
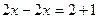 или или 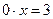 . .
Это уравнение не имеет корней, так как левая часть 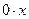 равна нулю при любом равна нулю при любом 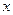 , а значит, не равна 3. [1, c.34] , а значит, не равна 3. [1, c.34]
Пример 2.
Решить уравнение 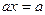 . .
Решение. Это уравнение содержит параметр 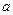 (переменную, которая в условии данной задачи сохраняет одно и то же значение). (переменную, которая в условии данной задачи сохраняет одно и то же значение).
Если 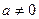 , то , то 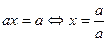 , т.е. , т.е.  - единственный корень уравнения. Если - единственный корень уравнения. Если 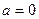 , то уравнение принимает вид , то уравнение принимает вид 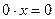 и его корнем является любое действительное число и его корнем является любое действительное число 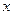 . [1, c.35] . [1, c.35]
Пример 3.
Решить уравнение
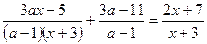 . .
Решение.
1) После приведения дробей к общему знаменателю 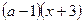 получим линейное уравнение получим линейное уравнение 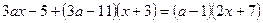 , равносильное исходному, при условии, что , равносильное исходному, при условии, что  , т.е. , т.е.  , , 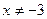 . .
2) После приведения подобных членов и сведения полученного уравнения к стандартному для линейного уравнения виду 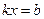 имеем имеем 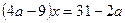 , (*) , (*)
3) а) Если 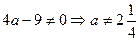 , то , то 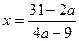 . Теперь необходимо исключить те значения параметра . Теперь необходимо исключить те значения параметра 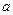 , при которых найденное значение , при которых найденное значение 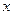 равно равно 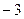 , чего не может быть по области определения (ОДЗ) исходного уравнения. Приравняем дробь , чего не может быть по области определения (ОДЗ) исходного уравнения. Приравняем дробь  к к 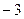 : :
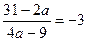 , , 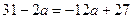 , , 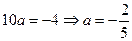 . .
Таким образом, при 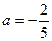 полученное в результате преобразования линейное уравнение имеет корень полученное в результате преобразования линейное уравнение имеет корень 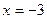 , посторонний для исходного уравнения. , посторонний для исходного уравнения.
б) Если 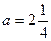 , то уравнение (*) примет вид , то уравнение (*) примет вид 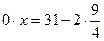 или или 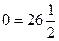 - неверное равенство, т.е. уравнение (*) не имеет корней. - неверное равенство, т.е. уравнение (*) не имеет корней.
Вообще, если уравнение не имеет корней, то говорят также, что множество корней уравнения пустое, и обозначают Ø.
Ответ. 1) При  , , 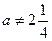 и и 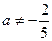 уравнение имеет единственное решение уравнение имеет единственное решение 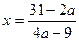 ; ;
2) при 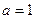 данное уравнение не имеет смысла; данное уравнение не имеет смысла;
3) при 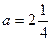 и и 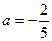 нет решений. нет решений.
Ответ можно записать короче:
1) если 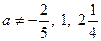 , то , то 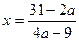 ; 2) если ; 2) если 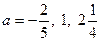 , то Ø. [14, c.42] , то Ø. [14, c.42]
§3.
Квадратные уравнения. Теорема Виета (прямая и обратная).
Определение.
Квадратным уравнением (или уравнением второй степени) называется уравнение вида  , где , где 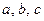 - заданные числа, причем - заданные числа, причем 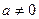 , а , а 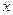 - неизвестное. Числа - неизвестное. Числа 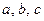 называются коэффициентами квадратного уравнения: называются коэффициентами квадратного уравнения: 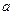 - коэффициент при квадрате неизвестного, - коэффициент при квадрате неизвестного, 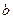 - коэффициент при неизвестном в первой степени, - коэффициент при неизвестном в первой степени,  - свободный член. - свободный член.
Квадратное уравнение 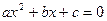 называется неполным, если хотя бы один из коэффициентов называется неполным, если хотя бы один из коэффициентов 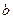 или или  равен нулю. равен нулю.
Неполное квадратное уравнение - это уравнение одного из следующих видов:
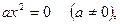
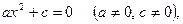
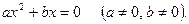
Покажем, как решаются неполные квадратные уравнения.
1. Уравнение 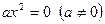 имеет единственный корень имеет единственный корень 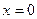 . .
2. Уравнение 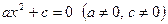 равносильно уравнению равносильно уравнению  . Возможны два случая. . Возможны два случая.
Если 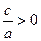 , то , то 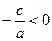 , и поэтому уравнение , и поэтому уравнение 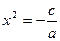 не имеет действительных корней. не имеет действительных корней.
Если 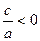 , то , то 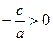 , и уравнение , и уравнение 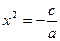 имеет два корня: имеет два корня: 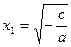 , , 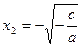 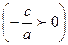 . .
Действительно, перенося в уравнении 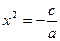 величину величину 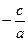 в левую часть, получаем в левую часть, получаем 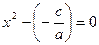 . .
Так как 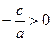 , то , то 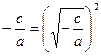 . Поэтому . Поэтому 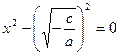 . .
Разложив левую часть этого уравнения на множители, получим 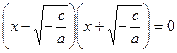 . .
Данное произведение равно нулю, если хотя бы один из сомножителей равен нулю.
Рассматривая 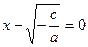 , получим , получим 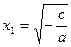 ; рассматривая ; рассматривая 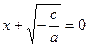 , находим , находим 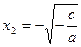 . .
Следовательно, уравнение 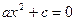 при при 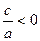 имеет два корня; имеет два корня; 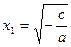 , , 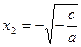 что и утверждалось. Ответ часто записывается в виде что и утверждалось. Ответ часто записывается в виде 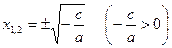 . .
Например, неполное квадратное уравнение 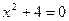 не имеет действительных корней. Для неполного квадратного уравнения не имеет действительных корней. Для неполного квадратного уравнения 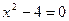 получаем получаем 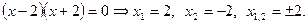
Это уравнение можно решить по-другому:
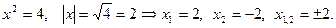
3. Уравнение 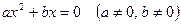 можно решить с помощью разложения его левой части на множители. Очевидно, что можно решить с помощью разложения его левой части на множители. Очевидно, что 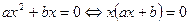 , откуда , откуда 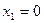 , , 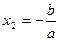 . Например, . Например, 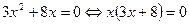 , откуда , откуда 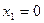 , , 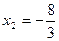 . .
В общем случае для решения квадратных уравнений применяется метод выделения полного квадрата. [5, c.120]
Применение этого метода поясним сначала на примерах.
Пример 1.
Решить квадратное уравнение 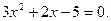
Решение. Разделим обе части уравнения на 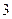 : :
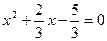 . .
Применим метод выделения полного квадрата: 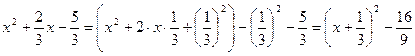 . .
Поэтому получим
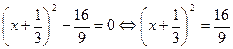 , ,
откуда 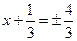 . Следовательно, . Следовательно,
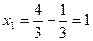 , , 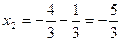 . .
Можно выделить полный квадрат в исходном уравнении и без предварительного деления на 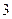 (коэффициент при квадрате неизвестного): (коэффициент при квадрате неизвестного):
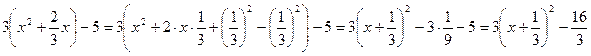 . .
Поэтому
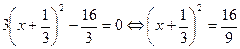 и т.д. [2, c.107] и т.д. [2, c.107]
Рассмотрим теперь квадратное уравнение общего вида
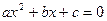  . (1) . (1)
Применим метод выделения полного квадрата. Для этого запишем левую часть уравнения в следующем виде:
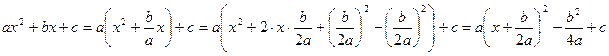 .Поэтому .Поэтому
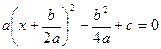 или или 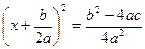 . (2) . (2)
Дальнейшее решение зависит от знака правой части полученного уравнения (2).
Так как 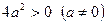 , то знак правой части совпадает со знаком выражения , то знак правой части совпадает со знаком выражения 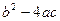 . [15, c.163] . [15, c.163]
Определение.
Выражение 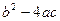 называется дискриминантом квадратного уравнения называется дискриминантом квадратного уравнения  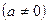 и обозначается буквой и обозначается буквой 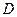 : : 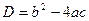 . .
Рассмотрим три случая: 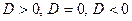 . .
1. 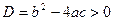 . .
В этом случае уравнение (2) можно записать так:
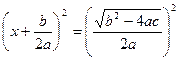 ; ;
следовательно,
 , ,
откуда
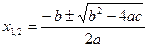 , (3) , (3)
или
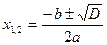 , (4) , (4)
где 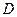 - дискриминант уравнения (1). - дискриминант уравнения (1).
Таким образом, в случае положительного дискриминанта, т.е. при 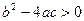 , уравнение , уравнение 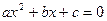 имеет два различных корня, которые можно найти по формуле (3) или (4). имеет два различных корня, которые можно найти по формуле (3) или (4).
2. 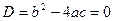 . .
В этом случае уравнение (2) принимает вид
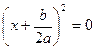 , ,
откуда  , т.е. , т.е. 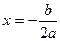 . .
Таким образом, если дискриминант равен нулю, т.е.  , то уравнение имеет единственный корень , то уравнение имеет единственный корень 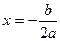 . .
Заметим, что формула (3) или, что то же, (4) применима и в случае 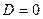 . В самом деле, эта формула дает единственный корень уравнения (1). Говорят также, что в этом случае квадратное уравнение имеет два равных корня: . В самом деле, эта формула дает единственный корень уравнения (1). Говорят также, что в этом случае квадратное уравнение имеет два равных корня: 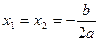 . Такое соглашение освобождает нас от специальных оговорок, относящихся к этому случаю при формулировке свойств квадратных уравнений. . Такое соглашение освобождает нас от специальных оговорок, относящихся к этому случаю при формулировке свойств квадратных уравнений.
3. 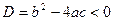 . .
В этом случае в правой части уравнения (2) стоит отрицательное число, а в левой части - неотрицательное (положительное или равное нулю). Следовательно, если 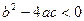 , то уравнение (2), а значит, и уравнение , то уравнение (2), а значит, и уравнение 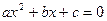 не имеют действительных корней. не имеют действительных корней.
Вывод.
Квадратное уравнение  имеет действительные корни только при дискриминанте имеет действительные корни только при дискриминанте  ; если ; если 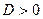 , то корни различные; если , то корни различные; если 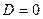 , то корни равные. Формула корней квадратного уравнения имеет вид (3) или (4). [15, c.165] , то корни равные. Формула корней квадратного уравнения имеет вид (3) или (4). [15, c.165]
По этой формуле можно находить и корни неполных квадратных уравнений, но проще вычислять их путем разложения левой части неполного квадратного уравнения на множители, как было показано.
Замечание 1. Если коэффициент 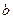 - четное число, т.е. - четное число, т.е. 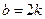 , то формула корней квадратного уравнения примет вид , то формула корней квадратного уравнения примет вид
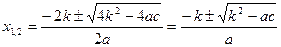 . [2, c.114] . [2, c.114]
Например, вычислим корни уравнения 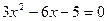 (заметим, что уравнение имеет действительные корни, так как (заметим, что уравнение имеет действительные корни, так как 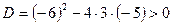 ): ):
 . .
Замечание 2. Если коэффициент 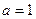 , то квадратное уравнение принимает вид , то квадратное уравнение принимает вид 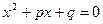 . Такое квадратное уравнение называется приведенным квадратным уравнением. Всякое квадратное уравнение . Такое квадратное уравнение называется приведенным квадратным уравнением. Всякое квадратное уравнение 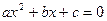 можно привести к виду можно привести к виду  делением обеих частей уравнения на делением обеих частей уравнения на 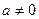 . [2, c.117] . [2, c.117]
Найдем корни приведенного квадратного уравнения. В формуле (3) полагаема 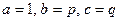 . Тогда . Тогда
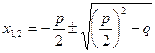 - формула корней приведенного квадратного уравнения - формула корней приведенного квадратного уравнения 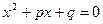 . .
Например, решим уравнение 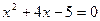 : :
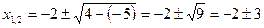 , ,
Откуда 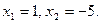
Пример
2.
Решить уравнение  . .
Решение. Разложив знаменатели на множители, имеем
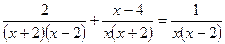 . .
После приведения дробей к общему знаменателю 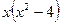 получим уравнение получим уравнение 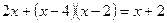 или или 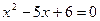 , равносильное исходному уравнению, при условии, что , равносильное исходному уравнению, при условии, что 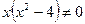 , т.е. , т.е. 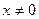 , ,  . Находим корни приведенного квадратного уравнения: . Находим корни приведенного квадратного уравнения:
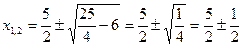 , ,
откуда 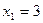 , , 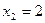 . Так как . Так как 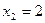 не удовлетворяет ограничению не удовлетворяет ограничению 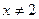 (не входит в ОДЗ исходного уравнения), то, следовательно, исходное уравнение имеет единственный корень (не входит в ОДЗ исходного уравнения), то, следовательно, исходное уравнение имеет единственный корень 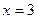 . [2, c.124] . [2, c.124]
Теорема Виета. Если квадратное уравнение  имеет действительные корни имеет действительные корни  и и 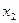 , то их сумма равна , то их сумма равна 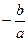 и произведение равно и произведение равно 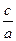 : :
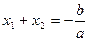 , , 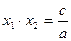 . (5) . (5)
Формулы (5) называются формулами Виета.
Доказательство. По условию дискриминант квадратного уравнения  . Тогда по формуле (4) уравнение имеет два корня: . Тогда по формуле (4) уравнение имеет два корня:
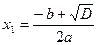 , , 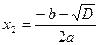 . .
Найдем сумму и произведение корней:
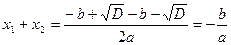 , ,
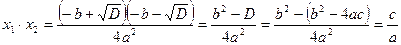 , ,
и формулы (5) получены.
Теорема Виета устанавливает связь между корнями квадратного уравнения и его коэффициентами.
Для приведенного квадратного уравнения 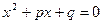 с дискриминантом с дискриминантом 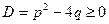 формулы (5) принимают вид формулы (5) принимают вид
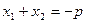 , , 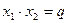 . (6) . (6)
Полученные для приведенного квадратного уравнения формулы Виета читаются так: сумма корней приведенного квадратного уравнения равна коэффициенту при неизвестном в первой степени, взятому с противоположным знаком, а произведение корней равно свободному члену.
Если корни квадратного уравнения действительные 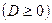 , то формулы Виета позволяют по знакам коэффициентов уравнения определить знаки корней. Например, если , то формулы Виета позволяют по знакам коэффициентов уравнения определить знаки корней. Например, если 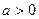 , , 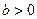 , , 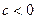 (и, следовательно, (и, следовательно, 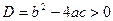 ), то ), то 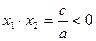 и корни имеют разные знаки. Так как при этом и корни имеют разные знаки. Так как при этом  , то отсюда следует, что больший по модулю корень отрицателен (сумма двух чисел разных знаков отрицательная!). [5, c.126] , то отсюда следует, что больший по модулю корень отрицателен (сумма двух чисел разных знаков отрицательная!). [5, c.126]
Теорема (обратная теореме Виета). Если числа 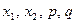 таковы, что таковы, что 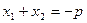 , , 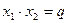 , то , то  и и 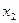 - корни уравнения - корни уравнения 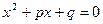 . .
В теореме Виета для приведенного квадратного уравнения 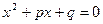 утверждалось, что для его корней утверждалось, что для его корней  , , 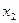 и коэффициентов и коэффициентов 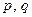 справедливы формулы (6). справедливы формулы (6).
В обратной теореме Виета утверждается: если для чисел 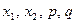 справедливы формулы (6), то справедливы формулы (6), то  и и 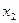 - корни приведенного квадратного уравнения - корни приведенного квадратного уравнения 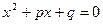 . .
Доказательство. Рассмотрим 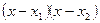 и получим и получим 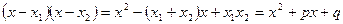 . Очевидно, что . Очевидно, что 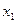 и и 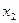 - корни уравнения - корни уравнения 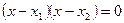 и, значит, уравнения и, значит, уравнения 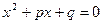 . [5, c.127] . [5, c.127]
Теорема Виета и теорема, обратная ей, часто применяются при решении различных задач.
Пример 3.
Не решая уравнения 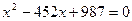 , определить знаки его корней. , определить знаки его корней.
Решение. Дискриминант этого уравнения положителен, так как 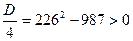 . Следовательно, уравнение имеет действительные корни . Следовательно, уравнение имеет действительные корни 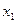 и и 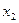 . По теореме Виета . По теореме Виета 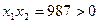 ; корни имеют одинаковые знаки. Так как по теореме Виста ; корни имеют одинаковые знаки. Так как по теореме Виста 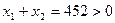 , то корни , то корни  и и 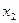 - положительные. [2, c.119] - положительные. [2, c.119]
Пример 4.
Составить приведенное квадратное уравнение, корни которого 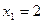 , , 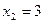 . .
Решение. По обратной теореме Виета 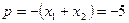 , , 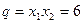 . Искомое уравнение . Искомое уравнение  . [2, c.119] . [2, c.119]
§4.
Разложение квадратного трехчлена на множители.
Рассмотрим квадратный трехчлен 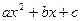 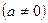 . .
Квадратный трехчлен - это многочлен второй степени. Значения  , при которых квадратный трехчлен обращается в нуль, называются корнями квадратного трехчлена. Для нахождения корней квадратного трехчлена нужно решить квадратное уравнение , при которых квадратный трехчлен обращается в нуль, называются корнями квадратного трехчлена. Для нахождения корней квадратного трехчлена нужно решить квадратное уравнение  . .
Мы уже знаем, что число действительных корней квадратного уравнения, а значит, и квадратного трехчлена зависит от знака дискриминанта 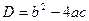 . Пусть дан квадратный трехчлен . Пусть дан квадратный трехчлен 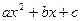 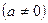 с неотрицательным дискриминантом с неотрицательным дискриминантом 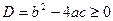 . .
Теорема. Если  и и 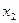 - корни квадратного трехчлена - корни квадратного трехчлена 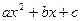 , то , то 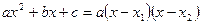 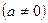 . (1) . (1)
Доказательство. Так как  и и 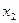 - корни квадратного уравнения - корни квадратного уравнения 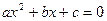 с дискриминантом с дискриминантом 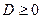 , то по теореме Виета , то по теореме Виета
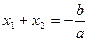 , , 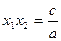 . .
Поэтому
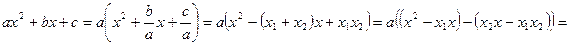 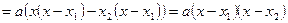 . .
Полученное равенство (1) называется формулой разложения квадратного трехчлена на линейные множители. [5, c.129]
Пример 1.
Упростить выражение 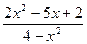 . .
Решение. Для квадратного трехчлена 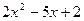 дискриминант дискриминант 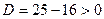 . Найдем корни трехчлена, решив квадратное уравнение . Найдем корни трехчлена, решив квадратное уравнение 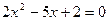 . Получим . Получим 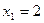 и и 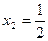 . Поэтому по формуле (1) . Поэтому по формуле (1) 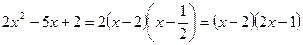 . Следовательно, . Следовательно,
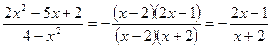 . [2, c.121] . [2, c.121]
Пример 2.
Доказать, что выражение
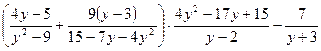
при всех допустимых значениях 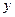 есть величина постоянная. есть величина постоянная.
Решение. 1) Разложим знаменатель второй дроби на линейные множители. Решив уравнение 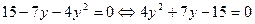 , найдем , найдем 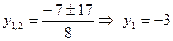 , , 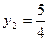 . Получаем разложение квадратного трехчлена: . Получаем разложение квадратного трехчлена: 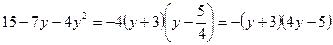 . .
2) 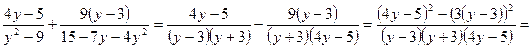
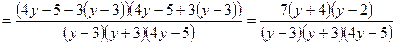 ; ;
3) 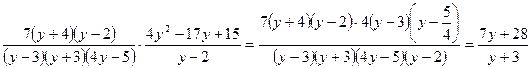 ; ;
4) 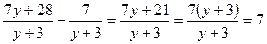 - величина, постоянная при всех допустимых значениях - величина, постоянная при всех допустимых значениях 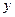 (т.е. при любых значениях (т.е. при любых значениях 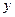 , для которых , для которых 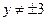 , ,  , , 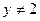 ). [5, c.130] ). [5, c.130]
§5.
Уравнения, приводимые к линейным и квадратным.
Уравнение вида
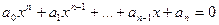 ( (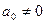 , , 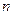 - натуральное) - натуральное)
называется алгебраическим уравнением n
-й
степени. Его левая часть - многочлен n
-й
степени относительно  . Уравнение первой степени и квадратное уравнение являются его частными случаями при . Уравнение первой степени и квадратное уравнение являются его частными случаями при 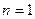 и и 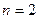 соответственно. соответственно.
Уравнения, в которых неизвестное содержится под знаком корня, называются иррациональными.
Всякое иррациональное уравнение с помощью элементарных преобразований (умножения, деления, возведения в целую степень обеих
частей уравнения) может быть сведено к рациональному алгебраическому уравнению. При этом следует иметь в виду, что полученное
рациональное алгебраическое уравнение может оказаться не эквивалентным исходному иррациональному уравнению, а именно может
содержать «лишние» корни, которые не будут корнями исходного
иррационального уравнения. Поэтому, вычислив корни полученного
алгебраического уравнения, необходимо проверить, будут ли все они
также и корнями исходного иррационального уравнения.
В общем случае трудно указать какой-либо универсальный метод решения любого иррационального уравнения, так как желательно, чтобы в результате преобразований исходного иррационального уравнения получилось не просто какое-то рациональное алгебраическое уравнение, среди корней которого будут и корни данного иррационального уравнения, а рациональное алгебраическое уравнение, образованное из многочленов как можно меньшей степени. Желание получить рациональное алгебраическое уравнение, образованное из многочленов как можно меньшей степени, вполне естественно, так как нахождение всех корней рационального алгебраического уравнения само по себе может оказаться довольно трудной задачей, решать которую полностью мы можем лишь в весьма ограниченном числе случаев. [23, c.107]
Рассмотрим примеры решения некоторых алгебраических уравнений степени 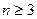 , а также иррациональных уравнений. , а также иррациональных уравнений.
Пример 1.
Решить уравнения:
а) 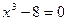 ; б) ; б) 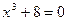
Решение. Оба уравнения можно решить разложением левой части на множители. Проще поступить по-другому:
а)  ; ;
б) 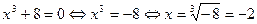 . [5, c.131] . [5, c.131]
Пример 2.
Решить уравнение 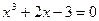 . .
Решение. Используем разложение на множители:
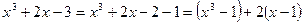 или или 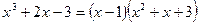 . .
Поэтому 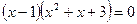 , откуда , откуда 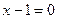 и и 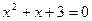 . Получим . Получим 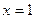 ; дискриминант квадратного уравнения ; дискриминант квадратного уравнения 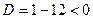 ; следовательно, квадратное уравнение действительных корней не имеет. ; следовательно, квадратное уравнение действительных корней не имеет.
Значит, 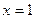 - единственный действительный корень данного уравнения. [5, c.131] - единственный действительный корень данного уравнения. [5, c.131]
Пример 3.
Решить уравнение 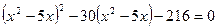 . .
Решение. Заметим важную особенность уравнения: его левая часть содержит неизвестное 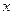 в виде выражения в виде выражения 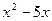 . Поэтому для решения этого уравнения используем метод введения нового неизвестного. Пусть . Поэтому для решения этого уравнения используем метод введения нового неизвестного. Пусть  , где , где 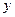 - новое неизвестное. Тогда данное уравнение приводится к квадратному уравнению относительно - новое неизвестное. Тогда данное уравнение приводится к квадратному уравнению относительно 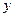 : : 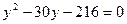 . .
Решая его, получаем 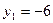 , , 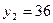 . .
Теперь найдем 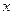 . Решая уравнение . Решая уравнение 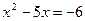 или или  , ,
получаем 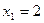 , , 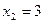 . .
Решая уравнение 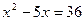 или или 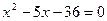 , ,
получаем 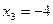 , , 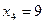 . .
Итак, 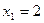 , , 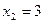 , , 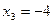 , , 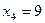 - все корни данного уравнения. - все корни данного уравнения.
Отметим, что без введения нового неизвестного решить данное уравнение четвертой степени было бы затруднительно. [5, c.132]
Пример 4.
Решить биквадратное уравнение 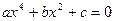 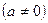 . .
Решение. Биквадратное уравнение - важный частный случай уравнения четвертой степени. Заменой 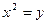 биквадратное уравнение приводится к квадратному уравнению биквадратное уравнение приводится к квадратному уравнению 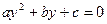 , которое имеет действительные корни только в случае, когда его дискриминант , которое имеет действительные корни только в случае, когда его дискриминант 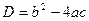 неотрицательный. Тогда возможны следующие случаи, (в зависимости от корней неотрицательный. Тогда возможны следующие случаи, (в зависимости от корней 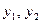 вспомогательного квадратного уравнения): вспомогательного квадратного уравнения):
1) 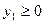 , , 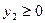 ; биквадратное уравнение имеет четыре действительных корня: ; биквадратное уравнение имеет четыре действительных корня: 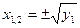 , ,  . .
2) 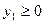 , , 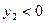 ; биквадратное уравнение имеет два действительных ; биквадратное уравнение имеет два действительных
корня: 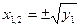 . .
Очевидно, аналогично и при 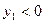 , , 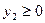 . .
3) 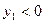 , , 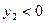 ; биквадратное уравнение не имеет действительных корней. ; биквадратное уравнение не имеет действительных корней.
Например, решим биквадратное уравнение 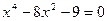 . Полагаем . Полагаем 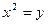 . Тогда . Тогда 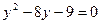 ; дискриминант ; дискриминант 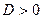 ; корни ; корни 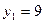 , , 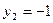 . Решая уравнение . Решая уравнение 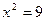 , получаем , получаем 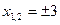 . Уравнение . Уравнение 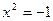 действительных корней не имеет. [23, c.103] действительных корней не имеет. [23, c.103]
Пример 5.
Решить уравнение 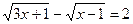 . .
Решение. Запишем уравнение в виде 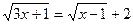 и возведем обе части его в квадрат: и возведем обе части его в квадрат:
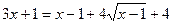 или или 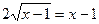 , откуда , откуда 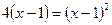 , т.е. , т.е. 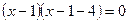 . Следовательно, . Следовательно,  , , 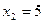 . Проверка показывает, что числа . Проверка показывает, что числа 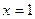 , , 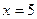 удовлетворяют исходному уравнению. удовлетворяют исходному уравнению.
Ответ: 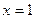 , , 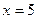 . [15, c.185] . [15, c.185]
§6.
Уравнения третей степени.
Будем рассматривать уравнение третей степени вида 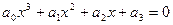 , где , где 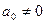 , , 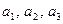 - любые коэффициенты. Левая часть – это многочлен третей степени, поэтому уравнение имеет три корня (возможно комплексные и совпадающие). Разделим данное уравнение на - любые коэффициенты. Левая часть – это многочлен третей степени, поэтому уравнение имеет три корня (возможно комплексные и совпадающие). Разделим данное уравнение на  , тогда получим: , тогда получим:
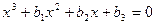 , (1) , (1)
Преобразуем это уравнение так, чтобы исчез член с квадратом неизвестного. Если положить
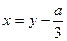
и подставить это выражение в наше уравнение, то после несложных выкладок получится более простое уравнение
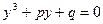 , (2) , (2)
которое называется приведенным уравнением третей степени.
Таким образом, остается решить уравнение (2). Полагаем 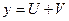 , где , где 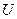 и и 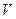 – два новых вспомогательных неизвестных, и, подставляя это выражение – два новых вспомогательных неизвестных, и, подставляя это выражение 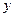 в уравнение (2), мы получим: в уравнение (2), мы получим:
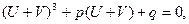
или, раскрыв скобки и перегруппировав члены:
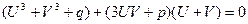 , (3) , (3)
Так как вместо одного неизвестного ввели две неизвестные 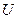 и и 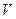 , то одно может быть выбрано произвольно, т.е. между , то одно может быть выбрано произвольно, т.е. между 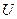 и и 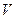 можем установить еще одну произвольную зависимость. Потребуем, чтобы можем установить еще одну произвольную зависимость. Потребуем, чтобы 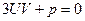 . .
Значит 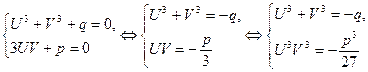
Мы видим, что 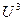 и и 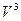 являются корнями приведенного квадратного уравнения являются корнями приведенного квадратного уравнения

Решая это уравнение, находим:
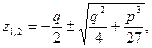
откуда
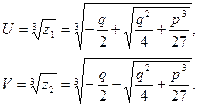
Итак, неполное уравнение (2) нам удалось решить алгебраически:
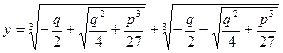 , (4) , (4)
Формула (4) называется формулой Кардана.
По этой формуле получается девять значений, а нас интересует только три значения. Нужные три значения найдем из условия
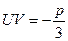 , (5) , (5)
Чтобы упростить систему поисков, поступим следующим образом: обозначим через 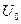 одно из значений одно из значений 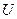 (любое), а через (любое), а через 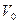 такое значение такое значение 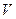 , чтобы , чтобы 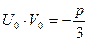 или или 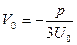 . Тогда остальные значения находятся по формулам: . Тогда остальные значения находятся по формулам:
 , , 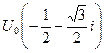 , ,
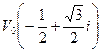 , , 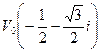 . .
Таким образом, получаем все три корня уравнения (2):
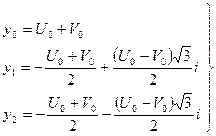 (6) (6)
Пример.
Определить по формуле Кардана корни уравнения 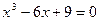 . .
Здесь 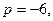 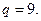 Следовательно, Следовательно,

Отсюда по формулам (6) получаем три корня уравнения:
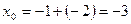
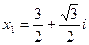
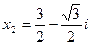 [23, c.99]. [23, c.99].
§7.
Уравнения четвертой степени.
Перейдем к исследованию уравнения
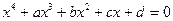 , (1) , (1)
четвертой степени. Рассмотрим его способ.
Перенесем три последних члена уравнения (1) в правую часть и прибавим к обеим частям 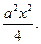
Тогда получится:
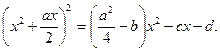
Затем прибавляем к обеим частям последнего уравнения сумму
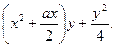
Уравнение примет вид:
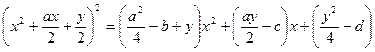 , (2) , (2)
Подберем вспомогательное неизвестное 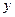 так, чтобы правая часть последнего уравнения превратилась в полный квадрат. Это будет очевидно, в том случае, когда так, чтобы правая часть последнего уравнения превратилась в полный квадрат. Это будет очевидно, в том случае, когда
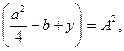 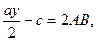 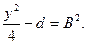
Но 
Поэтому должно быть:
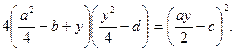
Если раскрыть скобки, то после некоторых преобразований получится также уравнение третьей степени относительно y
:
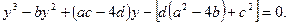
Пусть 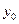 какой-нибудь корень этого уравнения. Подставляя его в уравнение (2), превратим его правую часть в полный квадрат какой-нибудь корень этого уравнения. Подставляя его в уравнение (2), превратим его правую часть в полный квадрат 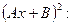
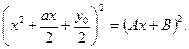
Отсюда
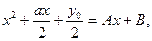
или

Эти два квадратных уравнения и дадут нам все четыре корня уравнения четвертой степени. [24, c.112]
Итак, решение уравнения четвертой степени сводится к решению одного уравнения третьей степени и двух уравнений второй степени.
Пример.
Найдем корни уравнения
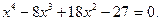
Здесь 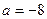 , ,
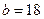 , ,
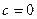 , ,
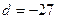 .
Следовательно, y
должно удовлетворять уравнению .
Следовательно, y
должно удовлетворять уравнению

Приводим последнее уравнение к трехчленному виду, полагая в нем
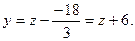
Получаем 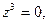 откуда откуда 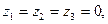 а потому а потому 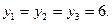
Затем находим  и и  . .

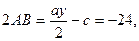
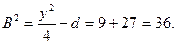
Мы видим, что 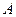 и и 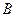 имеют положительные знаки, так как произведение имеют положительные знаки, так как произведение 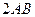 отрицательно. Поэтому полагаем отрицательно. Поэтому полагаем 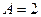 , ,
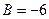 (с таким же успехом можно было взять (с таким же успехом можно было взять 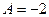 , , 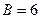 ). Отсюда получаются такие квадратные уравнения: ). Отсюда получаются такие квадратные уравнения:
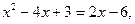
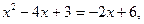
или
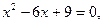
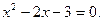
Решая первое уравнение, получаем 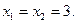
Решая второе уравнение, получаем 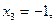 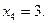
§8.
Уравнения, содержащие неизвестное под знаком
абсолютной величины.
Эти уравнения можно свести к уравнениям, не содержащим знака абсолютной величины, используя ее определение. Так, решение уравнения
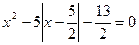 , (1) , (1)
сводится к решению двух уравнений с дополнительными условиями.
1. Если 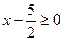 , то уравнение (1) приводится к виду , то уравнение (1) приводится к виду
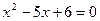 , (2) , (2)
Решения этого уравнения: 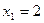 , , 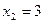 . Условию . Условию 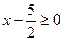
удовлетворяет лишь второй корень квадратного уравнения (2), и, следовательно, число 3 является корнем исходного уравнения (1).
2. Если 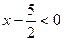 , то уравнение (1) приводится к виду , то уравнение (1) приводится к виду
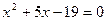 . .
Корнями этого уравнения будут числа 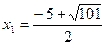 и и 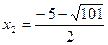 . Первый корень . Первый корень 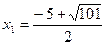 не удовлетворяет условию не удовлетворяет условию 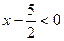 и поэтому не является решением уравнения (1). и поэтому не является решением уравнения (1).
Таким образом, решениями уравнения (1) будут числа 3 и 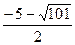 . .
Заметим, что коэффициенты уравнения, содержащего неизвестное под знаком абсолютной величины, можно подобрать так, что решениями будут все, значения неизвестного, принадлежащие некоторому промежутку числовой оси. Например, решим уравнение
 , (3) , (3)
Отметим на числовой оси точки 0 и 3 (нули функций, стоящих под знаком абсолютной величины). Эти точки разобьют числовую
ось на три промежутка (рис. 1):
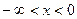 ; ; 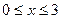 ; ; 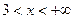
На этих промежутках:
1) при 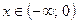 уравнение (3) приводится к виду уравнение (3) приводится к виду 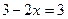 и в промежутке и в промежутке 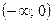 решений не имеет. решений не имеет.

0 3 х
Рис. 1
Аналогично при 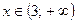 уравнение (3) приводится к виду уравнение (3) приводится к виду 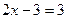 и в промежутке и в промежутке 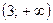 решений не имеет; решений не имеет;
2) при 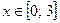 уравнение (3) приводится к виду уравнение (3) приводится к виду  , т.е. обращается в тождество. Следовательно, любое значение , т.е. обращается в тождество. Следовательно, любое значение 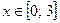 является решением уравнения (3). [23, 110] является решением уравнения (3). [23, 110]
ГЛАВА II. Использование способов решения
алгебраических уравнений на педагогической практике.
§1. Задачи, условие и этапы организации экспериментальной работы
по внедрению алгебраических уравнений
на уроках математики в 8 классах.
При проведении теоретических исследований были получены выводы о многообразии алгебраических уравнений, а также о том, что изучение алгебраических уравнений повышает уровень знаний по математике. Поэтому для подтверждения этих выводов наше эмпирическое исследование направлено на разрешение следующих задач:
1. Провести анализ содержания школьных учебников.
2. Определить методологические условия, способствующие качественному формированию знаний, умений и навыков в решении алгебраических уравнений.
3. Практически реализовать предложенную экспериментальную программу.
4. Провести сравнительный анализ результатов.
При проведении эмпирического исследования были использованы следующие методы: наблюдение, анкетирование, педагогический эксперимент, контрольные работы.
Для осуществления эксперимента были выбраны учащиеся 8 класса, средней полной общеобразовательной школы №4, Мартыновского района, хутора Малоорловский. Всего в исследовании приняло участие 28 учеников: 18 мальчиков и 10 девочек. Учитель математики охарактеризовал данный класс, как класс со средней успеваемостью, обучающейся без уклона на какую-либо дисциплину.
Исследование мы проводили на уроках математики, и оно включало в себя три этапа:
- Констатирующий.
- Формирующий.
- Контрольный.
В ходе констатирующего этапа мы осуществили наблюдение на уроках математике в 8 классе, анализировали содержание учебников алгебры, проводили анкетирование учителей, провели контрольную работу №1.
На этом этапе мы провели анализ учебников алгебры разных авторов. По нашему мнению наиболее доступным для учащихся языком написан учебник алгебры 7 класса, авторами которого являются Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров, Н.Е. Федорова, М.И. Шабунин. До того как ввести главу II, «Уравнения с одним неизвестным», авторы предлагают изучить главу I, «Алгебраические выражения», куда входят следующие параграфы:
§1. Числовые выражения.
§2. Алгебраические выражения.
§3. Алгебраические равенства. Формулы.
§4. Свойства арифметических действий.
§5. Правила раскрытия скобок.
Выше перечисленные параграфы, знакомят учащихся с темами, которые в дальнейшем помогут при изучении темы «Алгебраические уравнения». Изучив параграфы, входящих в главу I, учащиеся без труда освоят главу II:
§1. Уравнение и его корни.
§2. Решение уравнений с одним неизвестным, сводящихся к линейным.
§3. Решение задач с помощью уравнений.
Т.к. мы проводили наблюдение лишь в одном классе, наблюдали за деятельностью одного учителя, то наши заключения могут носить случайный характер. В связи с этим мы провели опрос учителей математики нескольких школ с тем, чтобы выявить, применяют ли они методы решения алгебраических уравнений, если применяют, то в каких случаях. Опрос проводился в форме анкеты (см. приложение 1). Шестнадцати респондентам предлагались 7 вопросов, на каждый из которых давались варианты ответов. Результаты анкетирования были занесены нами в таблицу 1.
Таблица №1. Обобщенные данные по результатам анкетирования.
| Номер
позиции
Номер
вопроса
|
1
|
2
|
3
|
Всего
|
| 1
|
11
65%
|
5
35%
|
0
0%
|
16
100%
|
| 2
|
9
55%
|
5
32%
|
2
13%
|
16
100%
|
| 3
|
10
60%
|
1
10%
|
5
30%
|
16
100%
|
| 4
|
10
60%
|
3
20%
|
3
20%
|
16
100%
|
| 5
|
8
50%
|
3
18%
|
5
32%
|
16
100%
|
| 6
|
2
28,5%
|
4
57%
|
1
14,5%
|
7
100%
|
| 7
|
7
45%
|
5
35%
|
4
20%
|
16
100
|
Из таблицы видно, что из шестнадцати опрошенных учителей 65% ответили, что недостаточно времени отводится программой для обучения учащихся предмету, 35% ответили, что вполне достаточно и ни один человек не ответил, что для обучения учащихся этому предмету отводится количество часов в избытке.
Итак, на вопрос – систематизируете ли вы знания учащихся на уроках математики – 55% учителей ответили – нет, 32% - не знаю, 13% - да. Результаты опроса показали, что большинство учителей считают, что нет системы в изложении данной темы. 60% всех учителей считают важным достижение повышения качества знаний учащихся, 30% - активности школьников в учении, 10% - исключение дублирования. При построении оптимальной системы уроков по теме «Алгебраические уравнения» 60% учителей использую методические журналы, остальные – дидактическую литературу и учебные пособия. 50% учителей считают, что трудности возникают в связи с большими затратами времени на изучение материала, 18% - отсутствие необходимой литературы и 32% - сложность для восприятия учащихся. 57% учителей используют алгебраические уравнения с целью получения прочных, осознанных знаний, остальные – для развития логического мышления и формирования познавательных интересов. На вопрос о необходимости использовать систематичность в обучении для лучшего усвоения и углубления знаний математического материала были получены следующие ответы: 45% считают необходимым использовать систематичность в обучении для лучшего усвоения учебного материала, 35% - нет, и 20% - только на факультативах.
Анализируя полученные ответы на вопросы анкеты, можно сделать вывод о том, что большинство учителей преподают тему «Алгебраические уравнения» не в системе, одни по причине большой затраты времени, другие в связи с отсутствием необходимой литературы.
Для определения эффективности использования разработанной нами системы необходимо сравнить уровень успеваемости учащихся до введения системы и после. Поэтому в ходе констатирующего этапа эмпирического исследования мы провели контрольную работу №1 (см. приложение №2). Задания, подобранные в ней, соответствовали уровню знаний учащихся, были средней сложности.
На основе результатов, полученных в ходе наблюдения, можно сделать вывод о том, что решение алгебраических уравнений с одной неизвестной различными способами способствует активизации самостоятельной деятельности, повышению интереса к предмету, развитию логического мышления, приросту знаний.
На формирующем этапе мы поставили следующие цели:
1. Внедрить на уроках математики в 8 классе материал, содержание которого раскрыто в теоретической части нашей дипломной работы.
2. Провести наблюдение за процессами осмысления, восприятия и запоминания учащимися данного материала.
3. Определить какие вопросы вызвали наибольшие затруднения у учащихся.
В ходе формирующего этапа эмпирического исследования рассматривать алгебраические уравнения с одной неизвестной предлагалось учащимся в качестве дополнительного материала, а так же на факультативах. Способы решения таких уравнений подробно описаны в главе I нашей дипломной работы.
На начальных этапах введения данной темы возникло множество трудностей, связанных прежде всего с тем, что исследование проводилось в 8 классе, где тема «Алгебраические уравнения» изучалась год назад и многие навыки при решении уравнений были забыты. Уравнения довались по следующей схеме: от более простых, к более сложным. Это позволило повысить эффективность воспроизведения памяти данной темы. На уроке алгебры объяснялась тема «Дробно-рациональные уравнения», на котором был изучен алгоритм решения этих уравнений. Приведем фрагмент этого урока.
| Этапы урока
|
Деятельность учителя
|
Деятельность учащихся
|
| II. Устный счет
IV. Закреп-ление.
|
Решить уравнения:
1) 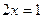 ; ;
2) 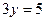 ; ;
3) 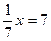 ; ;
4) 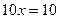 . .
Как найти неизвестное уменьшаемое?
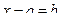
Как найти неизвестное вычитаемое?
Решим уравнение:
 . .
Что в этом уравнении является неизвестным?
Как найти неизвестное уменьшаемое?
Решим такое уравнение:
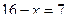
Что в это уравнении является неизвестным?
Как найти неизвестное вычитаемое?
Решим уравнение:
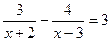 . .
Что делаем в первую очередь?
Каким мы воспользовались свойством?
Каким здесь воспользовались законом?
Будут ли найденные значения являться корнями уравнения?
|
1) 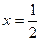 . .
2) 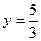 . .
3) 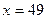 . .
4) 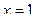 . .
Нужно к разн6ости прибавить вычитаемое.
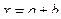
Нужно из уменьшаемого вычесть разность.
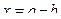
Уменьшаемое.
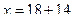
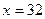
Вычитаемое.
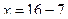
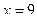
Приводим дроби к общему знаменателю.
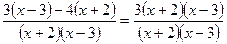
Умножим обе части уравнения на  , получим , получим
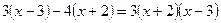 . .
Свойством сократимости.
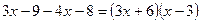
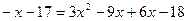
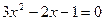
Сочетательным законом.
Решая это уравнение, находим его корни: 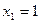 , , 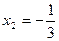 . .
Да, так как при подстановке этих значений в знаменатель, он не обращается в 0.
|
В ходе практической работы было выявлено множество позитивов. Отдельно можно выделить: учащиеся начинают осознавать, что без четкого анализа уравнения не возможен выбор правильного способа решения. Это ведет к развитию мыслительной активности учащихся, повышение которых положительно сказывается на всем процессе обучения. В этом случае они осознают, воспринимают и запоминают материал не только усилиями одной памяти, а прежде всего, усилиями мыслительных способностей.
В ходе контрольного этапа эмпирического исследования мы провели контрольную работу №2 (см. приложение №3) с целью выявления эффективности разработанной нами системы. Полученные результаты сравнили с результатами контрольной работы №1, проведенной на констатирующем этапе. Результаты двух контрольных работ мы приведем в следующем параграфе.
§2. Эффективность использования разработанной системы.
Для выявления эффективности используемой системы необходимо сравнить уровень успеваемости учащихся до введения разработанной системы и после, т.е. сравнить результаты контрольных работ.
Таблица №1. Оценки, полученные учащимися за контрольные работы на констатирующем и контрольном этапах.
| Контрольная работа №1
|
Контрольная работа №2
|
| 2 4 5 2 3 3 3 2 5 4
4 4 4 4 2 2 3 3 3 4
4 3 4 4 3 3 3 3
|
4 4 5 4 3 3 2 5 4 3
4 2 2 5 3 2 4 4 4 3
4 4 3 3 4 3 4 3
|
Из таблицы видно, что количество неудовлетворенных оценок после введения системы значительно снизилось. Это говорит о том, что уровень успеваемости у учащихся после введения системы незначительно, но повысился. Для наглядности представим результаты двух контрольных работ в виде диаграмм.
График результатов контрольной работы до введения системы
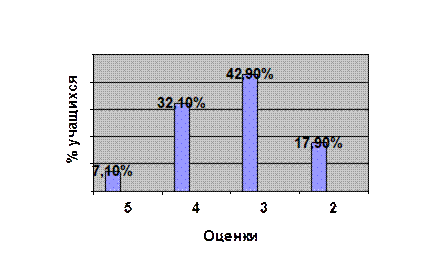
График результатов контрольной работы после введения системы
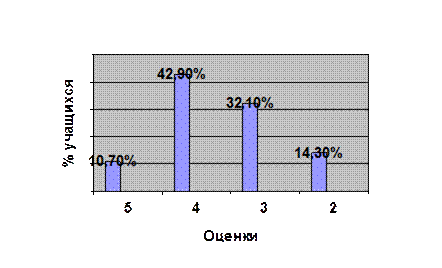
Проводя анализ контрольных работ, мы можем предположить, что системное изложение темы «Алгебраические уравнения с одной неизвестной» будет способствовать развитию логического мышления и творческой активности, так как у учащихся появляется интерес, а вследствие этого повышается успеваемость.
Сделав выводы, нами были выявлены условия, которые привели к таким результатам:
1. Временной фактор (контрольная работа №1 проводилась в начале четверти, а контрольная работа №2 по прошествии времени);
2. Ознакомление учащихся с различными видами и способами решения алгебраических уравнений с одной неизвестной;
3. Расширение круга задач, доступных учащимся 8 класса основной общеобразовательной школы.
Эти условия и помогли нам сделать общие выводы по нашему исследованию.
ЗАКЛЮЧЕНИЕ
Результаты теоретического и эмпирического исследования позволили нам сделать предположение о том, что в современной школе есть возможности применять предложенную методику изучения алгебраических уравнений и способов их решения. Это обеспечивает подготовку учащихся к восприятию начальных понятий, основ математики, использованию их в практической деятельности. Поэтому большое значение имеют такие вопросы школьного курса математики, которые учитывали бы современные тенденции развития образования, требующие от учащихся глубоких знаний математических понятий, прививающих учащимся стремление поиска новых путей, новых возможностей, новых подходов и разрешению жизненно важных вопросов, как традиционным путем, так и нестандартным.
На основе полученных результатов нашей дипломной работы мы пришли к выводу о том, что процесс изучения алгебраических уравнений доступен пониманию учащихся, может способствовать повышению качества их знаний и уровня обученности по математике, вооружает мощным математическим аппаратом для решения большого круга задач.
В связи с выше изложенным, мы считаем возможным рекомендовать учителям школ создавать условия для изучения алгебраических уравнений с тем, чтобы развить творческие способности и логическое мышление у учащихся, сформировать интерес к знаниям, а также активизировать их мыслительную деятельность.
Список литературы
4. Алгебра: Учебник для 7 кл. ср. шк./Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. и др. М.: Просвещение, 1991.
5. Алгебра: Учебник для 8 кл. общеобразоват. учреждений/Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. и др. М.: Просвещение, 1998.
6. Алгебра: Учебник для 9 кл. ср. шк./Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. и др. М.: Просвещение, 1992.
7. Алгебра: Учебник для 10-11 кл. ср. шк./Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. и др. М.: Просвещение, 1990.
8. Богатырев Г.И., Боковнев О.А. Математика для подготовительных курсов техникумов на базе 8 классов средней школы. М.: Наука, 1988.
9. Большой энциклопедический справочник. Математика. М: Большая российская энциклопедия, 1998.
10. Болтянский В.Г., Сидоров Ю.В., Шабушин М.И. Лекции и задачи по элементарной математике. М.: Наука, 1972.
11. Выгодский Н. Я. Справочник по элементарной математике. М.: Наука, 1979.
12. Глейзер Г.И. История математики в школе. М.: Наука, 1981.
13. Дорофеев Г.П., Потапов М.К. Пособие по математике для поступающих в ВУЗы. М.: Наука. гл. ред. физ.-мат. лит., 1976.
14. Задачи по математике. Алгебра. Справочное пособие. М.: Наука, 1987.
15. Колмогоров А.Н. Математика – наука и профессия. /Сост. Г.А. Гальперин. М.: Наука. гл. ред. физ.-мат. лит., 1988.
16. Кострикин А.И. Введение в алгебру. М.: Просвещение, 1979.
17. Литаренко Н.И. Правила решения уравнений. Математика в школе. 1996.
18. Мордкович А.Г. Алгебра и начало анализа. Учебное пособие для подготовительных отделений ВУЗов. М.: Высшая школа, 1987.
19. Методика преподавания математики в восьмилетней школе. Под общ. ред. Лепина С.Е. М.: Просвещение, 1965.
20. Методика преподавания математики в средней школе. Общая методика: учебное пособие для студентов физико-математических факультетов педагогических институтов. Под ред. В.А. Оганесяна. М.: Просвещение, 1980.
21. Муравин К.С., Крейдлин Е.Г. Сборник задач по алгебре для учащихся 6-8 классов. М.: Просвещение, 1964.
22. Окунев Л.Я. Высшая алгебра. М.: Просвещение, 1966.
23. Пособие по математике для поступающих в ВУЗы: Учебное пособие. Кутасов А.Д., Пиголкина Т.С., Чехлов В.И., Яковлева Т.Х. – под ред. Яковлева Г.Н. М.: Наука. гл. ред. физ.-мат. лит., 1988.
24. Потрягин Л.С. Математический анализ для школьников. М.: Наука, 1983.
25. Фихтенгольц Г.М. Основы математического анализа. т.1. М.: Наука, 1964.
26. Цыпкин А.Г. Справочник по математике для средних учебных заведений. М.: Наука, 1988.
27. Шавгулидзе Е.Т., Чирский В.Г. Уравнения элементарной математики.
Методы решения. М.: Наука, 1992.
28. Шклярский Д.О., Ченцов Н.Н., Яглош И.М., Избранные задачи теоремы элементарной математики. (Арифметика и алгебра). М.: Наука, 1976.
29. Шустеф Ф.М. Методика преподавания алгебры. Курс лекций. Минск, Высшая школа, 1967.
Приложение №1.
Анкета учителям.
Уважаемый коллега!
Мы проводим исследование состояния практики работы по изучению алгебраических уравнений в школьном курсе математики.
Просим вас ознакомиться с данной анкетой и максимально объективно ответить на ее вопросы, либо выбрать содержащиеся в ней утверждения.
Ваши ответы помогут нам определить пути дальнейшего совершенствования изучения алгебраических уравнений.
1. Достаточно ли Вам количества часов, отводимых программой, для обучения учащихся предмету, который вы преподаете?
1.1. Количество часов недостаточно.
1.2. Вполне достаточно.
1.3. Количество часов в избытке.
2. Существует ли, по-вашему, система в изложении темы «Алгебраические уравнения» в курсе алгебры 7-9 классов?
2.1. Да.
2.2. Нет.
2.3. Не знаю.
3. Что считаете наиболее важным результатом изучения алгебраических уравнений?
3.1. Достижение повышения качества знаний учащихся.
3.2. Активность школьников в учении.
3.3. Исключение дублирования.
4. Какие источники помогают Вам в построении оптимальной системы уроков по теме «Алгебраические уравнения?»
4.1. Методические журналы.
4.2. Дидактическая литература.
4.3. Учебные пособия.
5. Что затрудняет изложение данной темы в системе?
5.1. Большие затраты времени на изучение материала.
5.2. Сложность для восприятия учащихся.
5.3. Отсутствие необходимой литературы.
6. С какой целью Вы используете алгебраические уравнения?
6.1. С целью получения прочных, осознанных знаний.
6.2. Для развития логического мышления.
6.3. Для формирования познавательных интересов.
7. Считаете ли Вы необходимым использовать систематичность в обучении для лучшего усвоения учебного материала?
7.1. Да.
7.2. Нет.
7.3. Только на факультативах.
Спасибо за ответы!
Приложение №2.
Контрольная работа №1.
I вариант.
1. Решить уравнение:
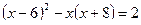
2. Найти координаты точки пересечения графиков функций:
 и и 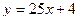
3. Решить уравнения:
а) 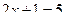 ; ;
б) 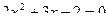 . .
4. Расстояние в 400 км скорый поезд прошел на час быстрее товарного. Какова скорость каждого поезда, если скорость товарного поезда на 20 км/ч меньше, чем второго?
II вариант.
1. Решить уравнение:
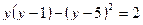
2. Найти координаты точки пересечения графиков функций:
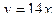 и и 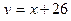
3. Решить уравнения:
а) 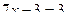 ; ;
б) 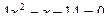 . .
4. Две бригады, работая вместе, закончили заготовку леса за 6 дней. Сколько дней потребовалось бы каждой бригаде на выполнение этой работы, если одной из бригад для этого требуется на 5 дней меньше, чем другой?
Приложение №3.
Контрольная работа №2.
I вариант.
1. Решить уравнение:
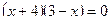
2. Решить уравнение:
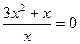
3. Упростить:

4. Решить уравнение:
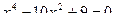
5. Прямоугольник, одна сторона которого на 2 см больше другой, имеет площадь, равную площади квадрата со стороной на 4 см меньше периметра прямоугольника. Найти стороны прямоугольника.
II вариант.
1. Решить уравнение:

2. Решить уравнение:
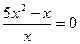
3. Упростить:
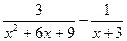
4. Решить уравнение
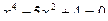
5. Прямоугольник, одна сторона которого на 8 см меньше стороны квадрата, а другая вдвое больше стороны квадрата, имеет площадь, равную площади этого квадрата. Найти стороны прямоугольника.
|