СОДЕРЖАНИЕ
1.Геометрические приложения интегралов
1.1 Геометрические приложения двойных интегралов………….. 3
1.2 Геометрические приложения тройных интегралов………….. 5
1.3 Геометрические приложения криволинейных интегралов… 6
1.4 Геометрические приложения поверхностных интегралов….. 8
2. Физические приложения интегралов
2.1 Физические приложения двойных интегралов……………… 10
2.2 Физические приложения тройных интегралов……………… 12
2.3 Физические приложения криволинейных интегралов……... 14
2.4 Физические приложения поверхностных интегралов……… 18
1.Геометрические приложения интегралов
1.1 Геометрические приложения двойных интегралов
1)Площадь плоской фигуры
Если f
(x,y
) = 1 в интеграле 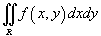 , то двойной интеграл равен площади области интегрирования R
. , то двойной интеграл равен площади области интегрирования R
.
Площадь области типа I (элементарной относительно оси Оy
) (рисунок 1) выражается через повторный интеграл в виде
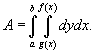
Аналогично, площадь области типа II (элементарной относительно оси Оx
) (рисунок 2) описывается формулой
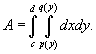
 |
 |
| Рис.1
|
Рис.2
|
2) Объем тела
Если f
(x,y
) > 0 в области интегрирования R
, то объем цилиндрического тела с основанием R
, ограниченного сверху поверхностью z = f
(x,y
), выражается формулой
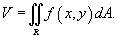
В случае, когда R
является областью типа I, ограниченной линиями 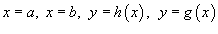 , объем тела равен , объем тела равен
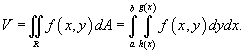
Для области R
типа II, ограниченной графиками функций 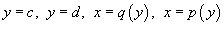 , объем соответственно равен , объем соответственно равен
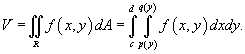
Если в области R
выполняется неравенство 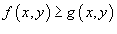 , то объем цилиндрического тела между поверхностями z
1
= f
(x,y
) и z
2
= g
(x,y
) с основанием R
равен , то объем цилиндрического тела между поверхностями z
1
= f
(x,y
) и z
2
= g
(x,y
) с основанием R
равен
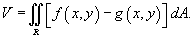
3) Площадь поверхности
Предположим, что поверхность задана функцией z = f
(x,y
), имеющей область определения R
. Тогда площадь такой поверхности над областью z
определяется формулой
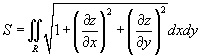
при условии, что частные производные 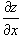 и и 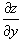 непрерывны всюду в области R
. непрерывны всюду в области R
.
Площадь и объем в полярных координатах
Пусть S
является областью, ограниченной линиями 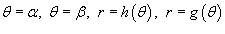 (рисунок 3). Тогда площадь этой области определяется формулой (рисунок 3). Тогда площадь этой области определяется формулой
 |
| Рис. 3 |
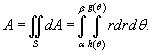
Объем тела, ограниченного сверху поверхностью 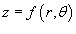 с основанием S
, выражается в полярных координатах в виде с основанием S
, выражается в полярных координатах в виде
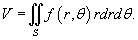
Пример
Вычислить площадь области R
, ограниченной линиями 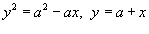 . .
Сначала определим точки пересечения двух заданных линий.
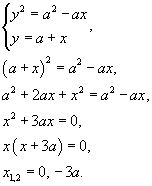
Следовательно, координаты точек пересечения равны
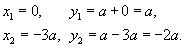
Область R
представлена на рисунке 5 выше. Будем рассматривать ее как область типа II. Для вычисления площади преобразуем уравнения границ:
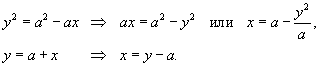
Получаем
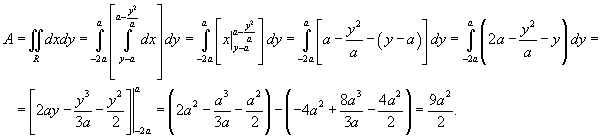
1.2 Геометрические приложения тройных интегралов
Геометрическое приложение
- вычисление объема
любого пространственного тела.
Объем тела
U
в декартовых координатах Oxyz
выражается формулой
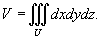
В цилиндрических координатах объем тела равен
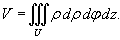
В сферических координатах, соответственно, используется формула
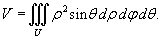
Пример
Найти объем шара x
2
+ y
2
+ z
2
≤ R
2
.
Вычислим объем части шара, расположенной в первом октанте (x
≥ 0, y
≥ 0, z
≥ 0), и затем умножим результат на 8. Получаем
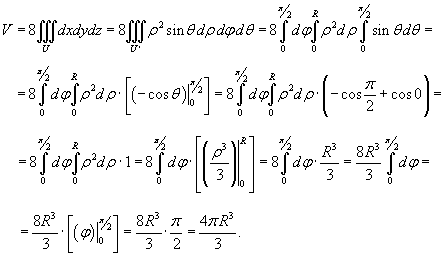
В результате получена известная формула для объема шара радиусом R
.
1.3 Геометрические приложения криволинейных интегралов
Криволинейные интегралы имеют многочисленные приложения в математике, физике и прикладных расчетах. В частности, с их помощью вычисляются
· Длина кривой;
· Площадь области, ограниченной замкнутой кривой;
· Объем тела, образованного вращением замкнутой кривой относительно некоторой оси.
Длина кривой
Пусть C
является гладкой, кусочно-непрерывной кривой, которая описывается вектором 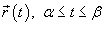 . Длина данной кривой выражается следующим криволинейным интегралом . Длина данной кривой выражается следующим криволинейным интегралом
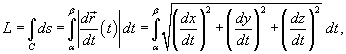
где 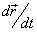 − производная, а − производная, а 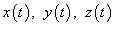 − компоненты векторной функции − компоненты векторной функции 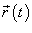 . .
Если кривая C
задана в плоскости, то ее длина выражается формулой
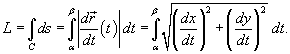
Если кривая C
представляет собой график заданной явно, непрерывной и дифференцируемой функции 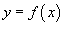 в плоскости Oxy
, то длина такой кривой вычисляется по формуле в плоскости Oxy
, то длина такой кривой вычисляется по формуле
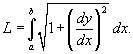
Наконец, если кривая C
задана в полярных координатах уравнением 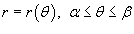 , и функция , и функция 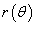 является непрерывной и дифференцируемой в интервале является непрерывной и дифференцируемой в интервале 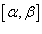 , то длина кривой определяется выражением , то длина кривой определяется выражением
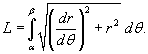
Площадь области, ограниченной замкнутой кривой
Пусть C
является гладкой, кусочно-непрерывной и замкнутой кривой, заданной в плоскости Oxy
(рисунок 1). Тогда площадь области R
, ограниченной данной кривой, определяется формулами
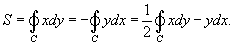
Здесь предполагается, что обход кривой C
производится против часовой стрелки.
Если замкнутая кривая C
задана в параметрическом виде 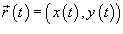 , то площадь соответствующей области равна , то площадь соответствующей области равна
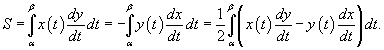
 |
 |
| Рис.1
|
Рис.2
|
Объем тела, образованного вращением замкнутой кривой относительно оси Ox
Предположим, что область R
расположена в верхней полуплоскости y ≥
0 и ограничена гладкой, кусочно-непрерывной и замкнутой кривой C
, обход которой осуществляется против часовой стрелки. В результате вращения области R
вокруг оси Ox
образуется тело Ω (рисунок 2). Объем данного тела определяется формулами
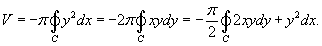
1.4 Геометрические приложения поверхностных интегралов
С помощью поверхностных интегралов вычисляются
- Площадь поверхности;
- Объем тела, ограниченного замкнутой поверхностью.
Площадь поверхности
Пусть S
является гладкой, кусочно-непрерывной поверхностью. Площадь поверхности
определяется интегралом
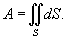
Если поверхность S
задана параметрически с помощью вектора
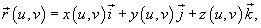
то площадь поверхности будет равна
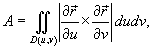
где D
(u,v
) − это область, в которой задана поверхность.
Если поверхность S
задана в явном виде функцией z
(x,y
), то площадь поверхности выражается формулой
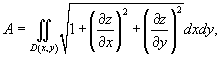
где D
(x,y
) − проекция поверхности S
на плоскость xy
.
Объем тела, ограниченного замкнутой поверхностью
Предположим, что тело ограничено некоторой гладкой, замкнутой поверхностью S
. Тогда объем тела
определяется по формуле
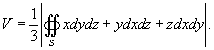
Пример
Вычислить площадь поверхности части параболоида 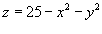 , лежащей выше плоскости xy
. , лежащей выше плоскости xy
.
Площади заданной поверхности равна
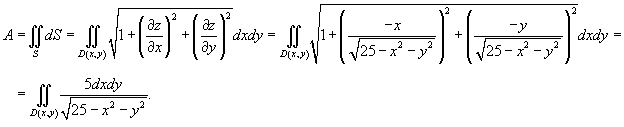
Переходя к полярным координатам, находим ответ:
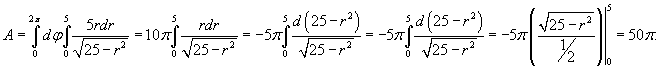
2. Физические приложения интегралов
2.1Физические приложения двойных интегралов
Масса и статические моменты пластины
Предположим, что плоская пластина изготовлена из неоднородного материала и занимает область R
в плоскости Oxy
. Пусть плотность пластины в точке (x, y
) в области R
равна 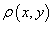 . Тогда масса пластины
выражается через двойной интеграл в виде . Тогда масса пластины
выражается через двойной интеграл в виде
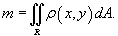
Статический момент пластины относительно оси
Ox
определяется формулой
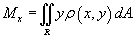
Аналогично находится статический момент пластины относительно оси
Oy
:
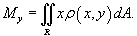
Координаты центра масс пластины
, занимающей область R
в плоскости Oxy
с плотностью, распределенной по закону 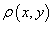 , описываются формулами , описываются формулами
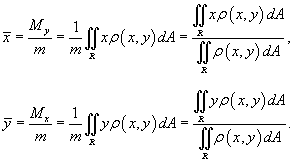
Для однородной пластины с плотностью 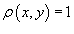 для всех (x, y
) в области R
центр масс определяется только формой области и называется центроидом
. для всех (x, y
) в области R
центр масс определяется только формой области и называется центроидом
.
Моменты инерции пластины
Момент инерции пластины относительно оси
Ox
выражается формулой
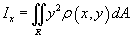
Аналогично вычисляется момент инерции пластины относительно оси
Oy
:
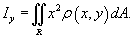
Полярный момент инерции пластины
равен
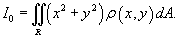
Заряд пластины
Предположим, что электрический заряд распределен по области R
в плоскости Oxy
и его плотность распределения задана функцией 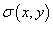 . Тогда полный заряд пластины
Q
определяется выражением . Тогда полный заряд пластины
Q
определяется выражением
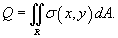
Среднее значение функции
Приведем также формулу дял расчета среднего значения некоторой распределенной величины. Пусть f
(x,y
) является непрерывной функцией в замкнутой области R
в плоскости Oxy
. Среднее значение функции μ
функции f
(x,y
) в области R
определяется формулой
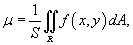
где 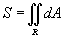 − площадь области интегрирования R
. − площадь области интегрирования R
.
Пример
Вычислить моменты инерции треугольника, ограниченного прямыми 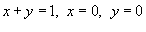 (рисунок 2) и имеющего плотность (рисунок 2) и имеющего плотность 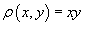 . .
Найдем момент инерции пластины относительно оси Ox
.
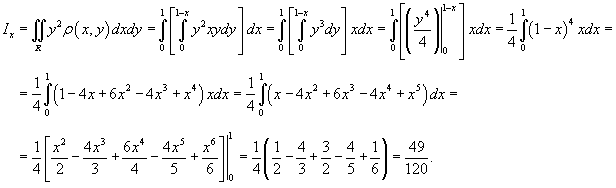
Аналогично вычислим момент инерции относительно оси Oy
.

2.2 Физические приложения тройных интегралов
Масса и статические моменты тела
Пусть тело занимает объем U
и его объемная плотность в точке M
(x,y,z
) задана функцией ρ
(x,y,z
). Тогда масса тела
m
вычисляется с помощью тройного интеграла:
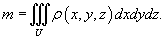
Статические моменты тела относительно координатных плоскостей Oxy, Oxz, Oyz
выражаются формулами
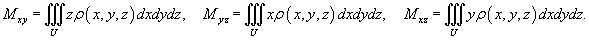
Координаты центра тяжести тела
вычисляются по формулам:
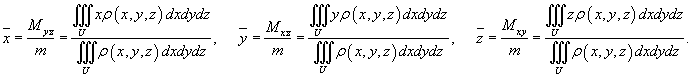
Если тело является однородным с плотностью ρ
(x,y,z
) = 1 для точек M
(x,y,z
) в области U
, то центр тяжести тела зависит только от геометрии тела и называется центроидом
.
Моменты инерции тела
Моменты инерции тела относительно координатных плоскостей Oxy, Oxz, Oyz
определяются выражениями
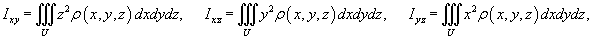
а моменты инерции тела относительно координатных осей Ox, Oy, Oz
вычисляются по формулам

Как видно, справедливы соотношения
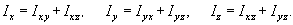
Моментом инерции тела относительно начала координат
называется интеграл
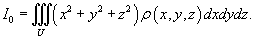
Момент инерции относительно начала координат можно выразить через моменты инерции относительно координатных плоскостей:
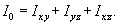
Тензор инерции
Используя рассмотренные выше 6 чисел Ix
, Iy
, Iz
, Ixy
, Ixz
, Iyz
, можно составить так называемую матрицу инерции
или тензор инерции
тела:
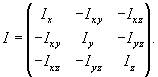
Данный тензор является симметричным, и, следовательно, его можно привести к диагональному виду при определенном выборе осей Ox', Oy', Oz'
. Значения диагональных элементов (после приведения тензора к диагональному виду) называются главными моментами инерции
, а указанные направления − собственными векторами
или главными осями инерции
.
Если тело вращается вокруг оси, не совпадаюшей с главной осью инерции, то оно будет испытывать вибрации при высоких скоростях вращения. Поэтому, при конструировании таких устройств необходимо, чтобы ось вращения совпадала с одной из главных осей инерции. Например, при замене шин автомобиля проводится их балансировка: небольшие грузики добавляются к колесам, чтобы обеспечить совпадение оси вращения с главной осью инерции и исключить вибрации.
Гравитационный потенциал и сила тяготения
Ньютоновым потенциалом тела
в точке P
(x,y,z
) называется интеграл
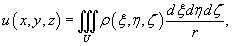
где ρ
(ξ,η,ζ
) − плотность тела, и 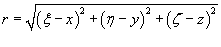 . .
Интегрирование выполняется по всему объему тела. Зная потенциал, можно вычислить силу притяжения материальной точки массы m
и заданного распределенного тела с плотностью ρ
(ξ,η,ζ
) по формуле
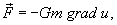
где G
− гравитационная постоянная.
Пример
Найти массу шара радиуса R
, плотность γ
которого пропорциональна квадрату расстояния от центра.
По условию, плотность γ
задана соотношением γ = ar
2
, где a
− некоторая постоянная, r
− расстояние от центра. Массу шара удобно вычислить в сферических координатах:
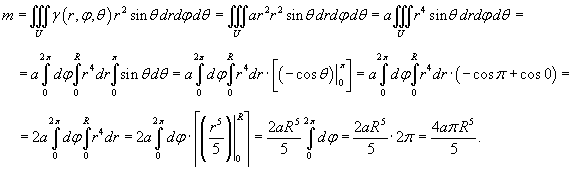
2.3 Физические приложения криволинейных интегралов
С помощью криволинейных интегралов вычисляются
1) Масса кривой;
2) Центр масс и моменты инерции кривой;
3) Работа при перемещении тела в силовом поле;
4) Магнитное поле вокруг проводника с током (Закон Ампера);
5) Электромагнитная индукция в замкнутом контуре при изменении магнитного потока (Закон Фарадея).
Рассмотрим эти приложения более подробно с примерами.
Масса кривой
Предположим, что кусок проволоки описывается некоторой пространственной кривой C
. Пусть масса распределена вдоль этой кривой с плотностью ρ
(x,y,z
). Тогда общая масса кривой
выражается через криволинейный интеграл первого рода
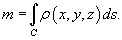
Если кривая C
задана в параметрическом виде с помощью векторной функции 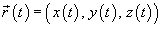 , то ее масса описывается формулой , то ее масса описывается формулой
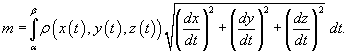
В случае плоской кривой, заданной в плоскости Oxy
, масса определяется как
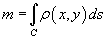
или в параметрической форме
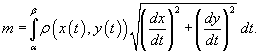
Центр масс и моменты инерции кривой
Пусть снова кусок проволоки описывается некоторой кривой C
, а распределение массы вдоль кривой задано непрерывной функцией плотности ρ
(x,y,z
). Тогда координаты центра масс кривой
определяются формулами
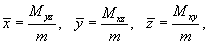
где
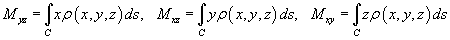
− так называемые моменты первого порядка
.
Моменты инерции относительно осей Ox, Oy и Oz
определяются формулами
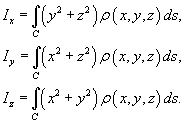
Работа поля
Работа при перемещении тела в силовом поле 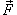 вдоль кривой C
выражается через криволинейный интеграл второго рода вдоль кривой C
выражается через криволинейный интеграл второго рода
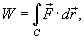
где 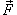 − сила, действующая на тело, − сила, действующая на тело, 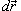 − единичный касательный вектор (рисунок 1). Обозначение − единичный касательный вектор (рисунок 1). Обозначение 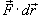 означает скалярное произведение векторов означает скалярное произведение векторов 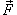 и и 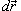 . .
Заметим, что силовое поле 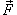 не обязательно является причиной движения тела. Тело может двигаться под действием другой силы. В таком случае работа силы не обязательно является причиной движения тела. Тело может двигаться под действием другой силы. В таком случае работа силы 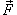 иногда может оказаться отрицательной. иногда может оказаться отрицательной.
Если векторное поля задано в координатной форме в виде
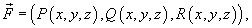
то работа поля вычисляется по формуле
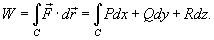
В частном случае, когда тело двигается вдоль плоской кривой C
в плоскости Oxy
, справедлива формула
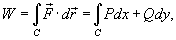
Где 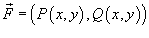
Если траектория движения C
определена через параметр t
(t
часто означает время), то формула для вычисления работы принимает вид
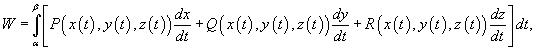
где t
изменяется в интервале от α
до β
. Если векторное поле 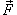 потенциально
, то работа по перемещению тела из точки A
в точку B
выражается формулой потенциально
, то работа по перемещению тела из точки A
в точку B
выражается формулой
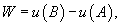 где где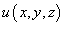 − потенциал поля. − потенциал поля.
 |
 |
| Рис.1
|
Рис.2
|
Закон Ампера
Криволинейный интеграл от магнитного поля с индукцией 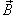 вдоль замкнутого контура C
пропорционален полному току, протекающему через область, ограниченную контуром C
(рисунок 2). Это выражается формулой вдоль замкнутого контура C
пропорционален полному току, протекающему через область, ограниченную контуром C
(рисунок 2). Это выражается формулой
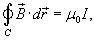
где 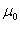 - магнитная проницаемость ваккуума
, равная - магнитная проницаемость ваккуума
, равная 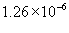 Н/м. Н/м.
Закон Фарадея
Электродвижущая сила
ε
, наведенная в замкнутом контуре C
, равна скорости изменения магнитного потока ψ
, проходящего через данный контур (рисунок 3).
 |
| Рис.3
|

Пример
Определить массу проволоки, имеющей форму отрезка от точки A
(1,1) до B
(2,4). Масса распределена вдоль отрезка с плотностью 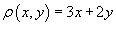 . .
Решение.
Составим сначала параметрическое уравнение прямой AB
. 
где параметр t
изменяется в интервале [0,1]. Тогда масса проволоки равна
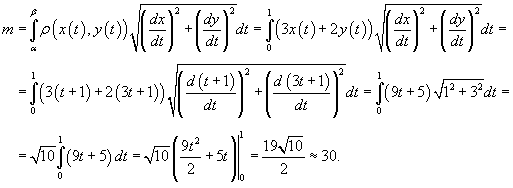
2.4 Физические приложения поверхностных интегралов
Поверхностные интегралы применяются во многих прикладных расчетах. В частности, с их помощью вычисляются
- Масса оболочки;
- Центр масс и моменты инерции оболочки;
- Сила притяжения и сила давления;
- Поток жидкости и вещества через поверхность;
- Электрический заряд, распределенный по поверхности;
- Электрические поля (теорема Гаусса в электростатике).
Масса оболочки
Пусть S
представляет собой тонкую гладкую оболочку. Распределение массы оболочки описывается функцией плотности 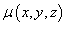 . Тогда полная масса оболочки
выражается через поверхностный интеграл первого рода по формуле . Тогда полная масса оболочки
выражается через поверхностный интеграл первого рода по формуле
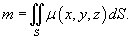
Центр масс и моменты инерции оболочки
Пусть распределение массы m
в тонкой оболочке описывается непрерывной функцией плотности 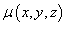 . Координаты центра масс оболочки
определяются формулами . Координаты центра масс оболочки
определяются формулами
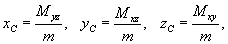
где
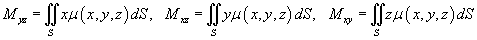
− так называемые моменты первого порядка относительно координатных плоскостей
x =
0, y =
0 и z =
0, соответственно.
Моменты инерции оболочки относительно осей Ox, Oy, Oz
выражаются, соответственно, формулами
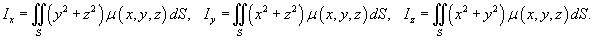
Моменты инерции оболочки относительно плоскостей xy, yz, xz
определяются формулами
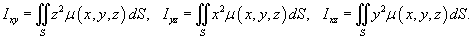
Сила притяжения поверхности
Пусть задана поверхность S
, а в точке (x
0
, y
0
, z
0
), не принадлежащей поверхности, находится тело массой m
(рисунок 1).
 |
 |
| Рис.1
|
Рис.2
|
Сила притяжения
между поверхностью S
и точечным телом m
определяется выражением
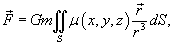
где 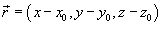 , G
- гравитационная постоянная, , G
- гравитационная постоянная, 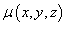 − функция плотности. − функция плотности.
Сила давления
Предположим, что поверхность S
задана вектором 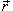 и находится под воздействием некоторой силы давления (это может быть плотина, крыло самолета, стенка баллона со сжатым газом и т.д.). Полная сила и находится под воздействием некоторой силы давления (это может быть плотина, крыло самолета, стенка баллона со сжатым газом и т.д.). Полная сила 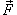 , созданная давлением , созданная давлением 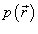 , находится с помощью поверхностного интеграла по формуле , находится с помощью поверхностного интеграла по формуле
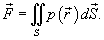
Давление, по определению, действует в направлении вектора нормали к поверхности S
в каждой точке. Поэтому, мы можем записать
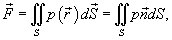
где  − единичный нормальный вектор к поверхности S
. − единичный нормальный вектор к поверхности S
.
Поток жидкости и поток вещества
Если в качестве векторного поля рассматривается скорость жидкости 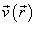 , то поток через поверхность S
называется потоком жидкости
. Он равен объему жидкости, проходящей через поверхность S
в единицу времени и выражается формулой , то поток через поверхность S
называется потоком жидкости
. Он равен объему жидкости, проходящей через поверхность S
в единицу времени и выражается формулой
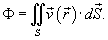
Аналогично, поток векторного поля 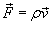 , где ρ − плотность, называется потоком вещества
и определяется выражением , где ρ − плотность, называется потоком вещества
и определяется выражением
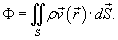
Он численно равен массе вещества, проходящего через поверхность S
в единицу времени.
Заряд поверхности
Пусть величина 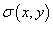 является плотностью распределения заряда по поверхности. Тогда полный заряд
, распределенный по проводящей поверхности S
выражается формулой является плотностью распределения заряда по поверхности. Тогда полный заряд
, распределенный по проводящей поверхности S
выражается формулой
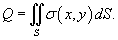
Теорема Гаусса
Поток электрического смещения
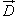 через замкнутую поверхность S
равен алгебраической сумме всех зарядов, расположенных внутри поверхности: через замкнутую поверхность S
равен алгебраической сумме всех зарядов, расположенных внутри поверхности:
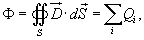
где 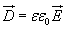 , , 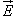 − напряженность электрического поля, ε
− относительная диэлектрическая проницаемость среды, − напряженность электрического поля, ε
− относительная диэлектрическая проницаемость среды, 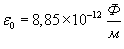 − диэлектрическая проницаемость вакуума. − диэлектрическая проницаемость вакуума.
Теорема Гаусса применима к любым замкнутым поверхностям. В случае поверхности с достаточной симметрией, данная теорема упрощает вычисление электрического поля. Теорему Гаусса рассматривают как один из основных постулатов теории электричества. Она входит в систему основных уравнений Максвелла.
Пример
Найти массу параболической оболочки, заданной уравнением 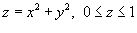 и имеющей плотность и имеющей плотность 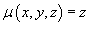 . .
Воспользуемся формулой
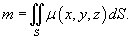
Проекция D
(x,y
) параболической поверхности S
на плоскость xy
представляет собой круг радиусом 1 с центром в начале координат. Следовательно, можно записать
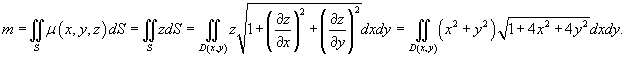
Переходя в подынтегральном выражении к полярным координатам, получаем
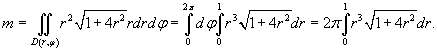
Сделаем подстановку 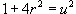 . Тогда . Тогда 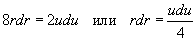 . Здесь u =
1 при r =
0, и . Здесь u =
1 при r =
0, и 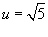 при r =
1. Следовательно, интеграл равен при r =
1. Следовательно, интеграл равен
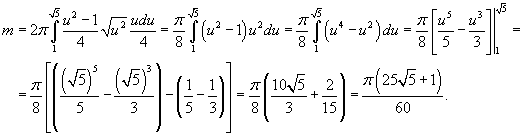
|