ЦЕНТРОСОЮЗ РОССИЙСКОЙ ФЕДЕРАЦИИ
СИБИРСКИЙ УНИВЕРСИТЕТ ПОТРЕБИТЕЛЬСКОЙ КООПЕРАЦИИ
Кафедра статистики и экономического прогнозирования
Контрольная работа
"Экономико-математические методы"
Новосибирск 2009
Задание 1
Производственная функция для райпо имеет вид 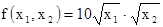 , где f – товарооборот, млн. руб.; x1
– производственная площадь, тыс. кв. м; x2
– численность работников, сотни чел. Рассмотрите изокванту уровня , где f – товарооборот, млн. руб.; x1
– производственная площадь, тыс. кв. м; x2
– численность работников, сотни чел. Рассмотрите изокванту уровня 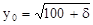 и найдите на ней точку С1
с координатами и найдите на ней точку С1
с координатами 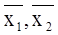 , где , где 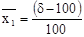 , и точку С2
с координатами , и точку С2
с координатами 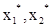 , где , где 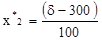 . Сделайте вывод о возможности замены ресурсов ( . Сделайте вывод о возможности замены ресурсов (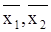 ) и ( ) и (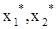 ). Полученные результаты изобразите графически. ). Полученные результаты изобразите графически.
Решение
Для производства некоторого изделия в количестве Y
единиц используются различные ресурсы, которые можно обозначить x1
, x2
, …..xn
. Очевидно, что и Y и x1
, x2
, …..xn
измеряются в определенных единицах измерения и имеют количественное выражение. Использую математические методы можно выразить значение одной величины через другую, в том числе Y через 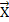 , где , где 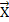 = (x1
, x2
, …..xn
)
. Функциональную зависимость Y = f ( = (x1
, x2
, …..xn
)
. Функциональную зависимость Y = f (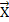 ) называют производственной функцией. ) называют производственной функцией.
Обозначим какое-то изделие через Y0
. Если установлено, что для его изготовления можно в n – мерном пространстве найти такие 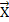 , что Y0
= f ( , что Y0
= f (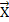 ). Найденные ). Найденные 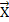 составят некоторое множество Q y
0.
Сказанное можно записать следующим образом Q y
0
= составят некоторое множество Q y
0.
Сказанное можно записать следующим образом Q y
0
= 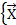 : : 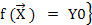 . .
Множество Q y
0
и называют изоквантой функции f (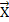 ). ).
Пусть имеются 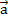 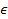 Q y
0
и Q y
0
и 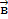 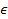 Q y
0
. Из понятия изокванты следует, что Q y
0
. Из понятия изокванты следует, что 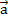 и и 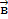 обеспечивают производство одного и того же количества продукта Y0
, т.е. являются в этом смысле взаимозаменяемыми. Для организаторов производства знание изокванты позволяет недостаток одних ресурсов компенсировать другими. обеспечивают производство одного и того же количества продукта Y0
, т.е. являются в этом смысле взаимозаменяемыми. Для организаторов производства знание изокванты позволяет недостаток одних ресурсов компенсировать другими.
Для производственной функции товарооборота (в млн. рублей), которая имеет вид: f (x1
, x2
) = 10 *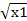 * * 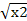 . .
(x1
– производственная площадь, тыс. кв. м;
x2
– численность работников, сотни чел.) и ее изокванты
Y0
= 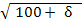 = = 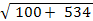 = = 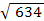 = 25,18 найдем координаты для точек C1
(а1
, в1
) и С2
(а2
, в2
). = 25,18 найдем координаты для точек C1
(а1
, в1
) и С2
(а2
, в2
).
Для точки C1
(а1
, в1
) известно, а1
= 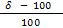 = = 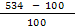 = = 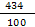 = 4,34. = 4,34.
Использую определение изокванты, получаем:
10 * 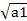 * * 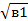 = = 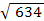 , или 100 * а1
* в1
= 634, или а1
* в1
= 6,34 , или 100 * а1
* в1
= 634, или а1
* в1
= 6,34
Отсюда, в1
= 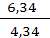 = 1,46, т.е. точка C1
имеет координаты (4,34; 1,46). = 1,46, т.е. точка C1
имеет координаты (4,34; 1,46).
Для точки C2
(а2
, в2
) известно, в2
= 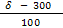 = = 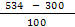 = = 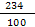 = 2,34. = 2,34.
Использую определение изокванты, получаем:
10 * 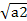 * * 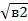 = = 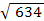 , или 100 * а2
* в2
= 634, или а2
* в2
= 6,34 , или 100 * а2
* в2
= 634, или а2
* в2
= 6,34
Отсюда, а2
= 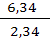 = 2,71, т.е. точка C2
имеет координаты (2,71; 2,34). = 2,71, т.е. точка C2
имеет координаты (2,71; 2,34).
Уравнение нашей изокванты имеет вид 10 *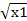 * * 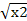 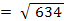
(при Y0
= 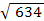 = 25,18) или x1
* x2
= 6,34. Уравнение такого вида представляет собой гиперболу, которую и изобразим схематически на графике ниже. = 25,18) или x1
* x2
= 6,34. Уравнение такого вида представляет собой гиперболу, которую и изобразим схематически на графике ниже.
Итак, 146 работников райпо, используя 4,34 тыс. кв. метров производственной площади, обеспечат товарооборот 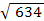 = 25,18 (млн. руб.), и такой же товарооборот могут обеспечить 234 работника райпо, используя площадь 2,71 тыс. кв. метров. = 25,18 (млн. руб.), и такой же товарооборот могут обеспечить 234 работника райпо, используя площадь 2,71 тыс. кв. метров.
Используя график этой функции, можно находить взаимозаменяемые пары (x1, x2).
X2
(сотни чел.) C2
(2,71; 2,34)
2.5
2.0
1.5 С1 (4,34; 1,46)
1.0
0.5
1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 X1
(тыс. кв. м)
Задание 2
Произведите классификацию товаров по следующей таблице эластичностей:
| Товар
|
Первый
|
Второй
|
Третий
|
| Первый
|
|
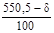
|
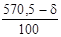
|
| Второй
|
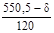
|
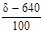
|
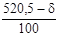
|
| Третий
|
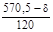
|
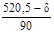
|
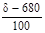
|
Решение
Преобразуем таблицу под наш вариант 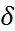 = 534 = 534
| товар
|
первый
|
второй
|
третий
|
| первый
|
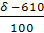 = = 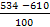 = – 0,76 = – 0,76
|
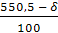 = =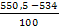 = 0,165 = 0,165
|
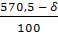 = = = 0,365 = 0,365
|
| второй
|
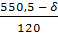 = =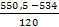 = 0,1375 = 0,1375
|
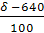 = = 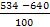 = – 1,06 = – 1,06
|
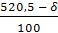 = =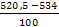 = – 1,135 = – 1,135
|
| третий
|
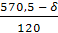 = =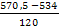 = 0,304 = 0,304
|
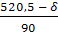 = =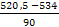 = – 0,15 = – 0,15
|
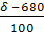 = = 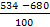 = – 1,46 = – 1,46
|
1. Введем определение эластичности товара.
Обозначим 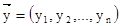 – спрос на товары, выраженный в некоторых единицах, и – спрос на товары, выраженный в некоторых единицах, и 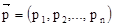 – цены на эти товары, т.е. pi
– цена на i – й товар; yi
– спрос на i – й товар. – цены на эти товары, т.е. pi
– цена на i – й товар; yi
– спрос на i – й товар.
Пусть рассматривается некоторый потребитель, например типичный представитель определенной социальной группы, и если для него удается 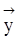 выразить через выразить через 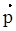 , т.е. , т.е. 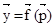 , то , то 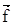 называется функцией спроса. называется функцией спроса.
Ввиду того, что 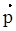 , ,  , , 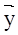 – n – мерные векторы, равенство – n – мерные векторы, равенство 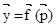 можно представить в координатной записи следующим образом: можно представить в координатной записи следующим образом: 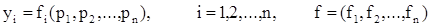 . .
Разумеется, в реальной ситуации спрос зависит не только от цен, но от многих других факторов. Поэтому введенное понятие имеет весьма ограниченное использование и применимо, в частности, для некоторой классификации товаров с позиции определенного потребителя.
Определим эластичность εij
формулой
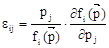 . .
Величина εij
является математической идеализацией процентного изменения спроса на i – й товар при увеличении на 1% цены на j-й товар.
Например, если ε23
=0,25, то это понимается так, что если цену на 3-й товар увеличить на 1%, то спрос на 2-й товар увеличится на 0,25%.
Эластичность εij
при i = j называется прямой, и она показывает, на сколько процентов изменится спрос на i-й товар при увеличении на 1% цены на этот же товар. Будем считать, что εii
‹ 0, т.е. увеличение цены на i-й товар приводит к снижению спроса на него.
Эластичность εij
при 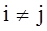 называется перекрестной, и она показывает влияние изменения цены одного товара на спрос другого. называется перекрестной, и она показывает влияние изменения цены одного товара на спрос другого.
Классификация товаров на основе прямой и перекрестной эластичности сводится к следующему:
– если |εii
| ‹ 1, то i-й товар называется малоэластичным;
– если |εii
|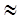 1, то i – й товар называется среднеэластичным; 1, то i – й товар называется среднеэластичным;
– если |εii
| › 1, то i – й товар называется высокоэластичным;
– если увеличение цены на j-й товар приводит к уменьшению спроса на i-й и наоборот, то эти товары называются взаимодополняемыми.
Математически это соответствует выполнению неравенств: εii
‹ 0, εji
‹ 0;
– если увеличение цены на j-й товар приводит к увеличению спроса на i-й товар и наоборот, то эти товары называются взаимозаменяемыми.
Математически это соответствует неравенствам εij
› 0, εji
› 0.
Таблица эластичностей принимает вид:
| товар
|
первый
|
второй
|
третий
|
| первый
|
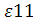 = – 0,76 = – 0,76
|
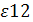 = 0,165 = 0,165
|
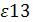 = 0,365 = 0,365
|
| второй
|
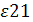 = 0,1375 = 0,1375
|
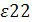 = – 1,06 = – 1,06
|
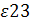 = – 1,135 = – 1,135
|
| третий
|
 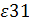 = 0,304 = 0,304
|
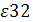 = – 0,15 = – 0,15
|
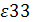 = – 1,46 = – 1,46
|
Так как |ε11
| = 0,76 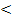 1, то первый товар малоэластичный; 1, то первый товар малоэластичный;
так как |ε22
| = 1,06 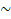  1, то второй товар среднеэластичный; 1, то второй товар среднеэластичный;
так как |ε33
| =1,46 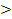 1, то третий товар высокоэластичный. 1, то третий товар высокоэластичный.
Поскольку ε12
= 0,165  0 и ε21
= 0,1375 0 и ε21
= 0,1375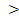 0, то первый и второй товары взаимозаменяемые. 0, то первый и второй товары взаимозаменяемые.
Поскольку ε13
= 0, 365  0 и ε31
= 0,304 0 и ε31
= 0,304  0, то первый и третий товары взаимозаменяемые. 0, то первый и третий товары взаимозаменяемые.
Поскольку ε23
= – 1,135 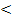 0 и ε32
= – 0, 15 0 и ε32
= – 0, 15 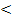 0, то второй и третий товары взаимодополняемые. 0, то второй и третий товары взаимодополняемые.
Задание 3
Дайте определение коэффициентов прямых затрат. Где они могут быть использованы?
Решение
1. Пусть народное хозяйство представлено n отраслями сферы материального производства. Каждая из отраслей производит один агрегированный продукт. Валовой выпуск этих продуктов отраслями обозначим x1
, x2
,…, xn
. Вся продукция xi
отрасли i, i=1, 2,…, n, делится на промежуточную Zi
и конечную yi
. Промежуточную продукцию потребляют в процессе производства сами отрасли. Конечная продукция выходит из сферы материального производства и предназначается для непроизводственного потребления.
На основе отчетных данных о деятельности отраслей за определенный период можно составить межотраслевой баланс. Обозначим xij
– объем продукта i-й отрасли, используемый за отчетный период j-й отраслью. Если представить, как распределяется валовая продукция каждой отрасли по другим отраслям и в сфере потребления, то получится система балансовых уравнений.
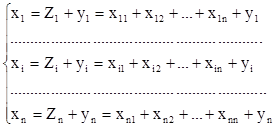 (1) (1)
Преобразуем систему уравнений:
 (2) (2)
Отношение 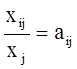 называется коэффициентом прямых затрат и содержательно означает объем продукции i-й отрасли, который требуется передать j-й отрасли, чтобы последняя произвела единицу своей валовой продукции. называется коэффициентом прямых затрат и содержательно означает объем продукции i-й отрасли, который требуется передать j-й отрасли, чтобы последняя произвела единицу своей валовой продукции.
Учитывая это, система уравнений примет вид:
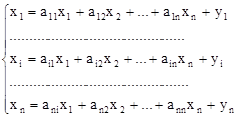 (3) (3)
Модель межотраслевого баланса может использоваться в планировании деятельности отраслей материального производства. Если технологии производства продуктов не меняются, то коэффициенты прямых затрат остаются неизменными.
Задание 4
В магазине самообслуживания работают две кассы с интенсивностью μ= (δ+300)/100 (треб./мин.) каждая. Входящий поток требований имеет интенсивность λ=(δ+400)/100 (треб./мин.). Рассчитайте долю времени простоя касс и среднюю длину очереди. Если интенсивность входящего потока станет равной λ=(700-δ)/10 (треб./мин.), то будет ли выполнено условие стационарности? Если будет, то во сколько раз увеличится средняя длина очереди?
Решение
К системам массового обслуживания (СМО) относятся магазины, рестораны, автозаправочные станции, аэродромы, автоматизированные телефонные станции и многие другие объекты. Общую схему СМО можно представить в следующем виде:
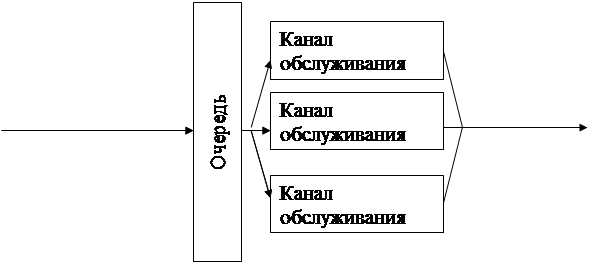
Поток
Входящий поток обслуженных
требований требований
Для входящего потока требований предположим, что интервалы между поступлениями соседних требований есть случайная величина X с показательным законом распределения, т.е. ее интегральная функция F(t) имеет вид:
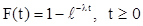 . .
Число λ (треб./ед. времени) называется интенсивностью входящего потока, и она показывает, сколько в среднем требований поступает в единицу времени.
Будем считать, что очередь не ограничена и требования обслуживаются в порядке поступления. Для обслуживания примем предположения, что все n каналов одинаковы и для каждого из них время обслуживания одного требования есть случайная величина Y, распределенная по показательному закону, т.е. ее интегральная функция имеет вид:
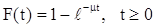 . .
Число μ (треб./ед. времени) называется интенсивностью обслуживания, и она показывает, сколько в среднем требований обслуживается одним каналом в единицу времени.
Обозначим  (α – параметр загрузки СМО) и предположим, что выполняется условие стационарности α < n или λ < μ * n. (α – параметр загрузки СМО) и предположим, что выполняется условие стационарности α < n или λ < μ * n.
Это условие означает, что интенсивность входящего потока меньше, чем суммарная интенсивность обслуживания.
При сформулированных предположениях можно рассчитать некоторые экономические показатели работы СМО, такие, например, как Рк
– доля времени работы К – каналов, К=0,1,…, n; L – средняя длина очереди и другие.
Формулы для вычисления p0
,…, pn,
L в общем случае довольно громоздки, поэтому приведем их для случая n = 2:
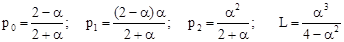 . .
Рассчитаем долю времени простоя касс и среднюю длину очереди для магазина самообслуживания, в котором работают две кассы с интенсивностью μ = (534+300)/100 (треб./мин.) каждая и входящий поток требований имеет интенсивность λ = (534+400)/100 (треб./мин.). Если интенсивность входящего потока станет равной λ=(700–534)/10 (треб./мин.), то будет ли выполнено условие стационарности? Если будет, то во сколько раз увеличится средняя длина очереди?
Вычислим λ (треб./ед. времени) интенсивностью входящего потока λ = 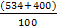 = 9,34 и μ (треб./ед. времени) интенсивностью обслуживания μ = = 9,34 и μ (треб./ед. времени) интенсивностью обслуживания μ = 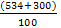 = 8,34. Отсюда, вычислим параметр загрузки СМО = 8,34. Отсюда, вычислим параметр загрузки СМО 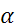 = =  = = 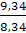 = 1, 12 и предположим, что выполняется условие стационарности = 1, 12 и предположим, что выполняется условие стационарности  < n или λ < μ * n (1,12 < 2; 9,34 < 8,34 * 2 = 16,68 – выполняются оба условия стационарности). < n или λ < μ * n (1,12 < 2; 9,34 < 8,34 * 2 = 16,68 – выполняются оба условия стационарности).
Вычислим Рк
– доля времени работы К – каналов, К=0,1 и L – средняя длина очереди:
Р0
= 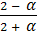 = = 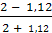 = 0,282 (Р0
= 28,2%) = 0,282 (Р0
= 28,2%)
L1
= 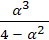 = = 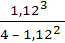 = = 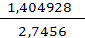 = 0,511 (треб.) = 0,511 (треб.)
Если интенсивность станет λ = 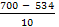 = 16,6 (треб./мин.), то, в силу выполнения условия стационарности (λ < μ * n, 16,6 < 8,34 * 2 = 16,68), вычислим среднюю длину очереди: = 16,6 (треб./мин.), то, в силу выполнения условия стационарности (λ < μ * n, 16,6 < 8,34 * 2 = 16,68), вычислим среднюю длину очереди:
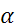 = =  = = 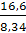 = 1,99 = 1,99
L2
= 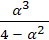 = = 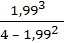 = = 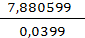 = 197,51 (треб.) = 197,51 (треб.)
 = = 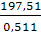 = 386,5. = 386,5.
Таким образом, при интенсивности обслуживания μ=8,34 (треб./мин.) и интенсивности входа λ=9,34 (треб./мин.) доля времени простоя касс составляет 28,2% времени, а средняя длина очереди равна 0,511 (треб.).
Если же интенсивность входа станет равной 16,6 (треб./мин.), то средняя длина очереди увеличится в 386,5 раза.
Литература
1. Айвазян С.А. и др. Прикладная статистика. Исследование зависимостей. – М.: Финансы и статистика, 1985
2. Гранберг А.Г. Математические модели социалистической экономики. – М.: Экономика, 1976
3. Иванилов Ю.П., Лотов А.В. Математические методы в экономике – М.: Наука, 1979
4. Лопатников Л.И. Экономико-математический словарь. – М.: Наука, 1987
5. Спирин А.А., Фомин Г.П. Экономико-математические методы и модели в торговле. – М: Экономика, 1988
6. Щедрин И.И., Кархов А.Н. Экономико-математические методы в торговле. – М.: Экономика, 1980
7. Шаланов Н.В. Экономико-математические методы в торговле: Учебное пособие. – Новосибирск: СибУПК, 1998
|