|
Исследовательская работа
Выполнил:
ученик 11 «А» класса
Дударев Александр
Руководитель:
учитель высшей категории
Поддельская В. Б
СОДЕРЖАНИЕ
Введение 2
История развития учения о комплексных числах 2
Действия с комплексными числами 4
Решение уравнений с комплексной переменной 7
Геометрия комплексных чисел 7
Возведение в степень и извлечение корня из комплексного числа 9
Заключение 11
Список литературы 12
КОМПЛЕКСНЫЕ ЧИСЛА
1
ВВЕДЕНИЕ
Впервые я узнал о комплексных числах в 5-ом классе, когда, читая энциклопедию, натолкнулся на это словосочетание. Я заинтересовался и решил прочитать статью до конца. Из неё я узнал, что вообще представляют собой комплексные числа, как с ними работать, где они применяются. На этом моё первое знакомство с комплексными числами закончилось. Я вспомнил о них лишь тогда, когда мой преподаватель по математике предложила мне тему работы в Малой Академии Наук – комплексные числа. Я сразу же согласился. Мой интерес возрос ещё больше, когда я узнал много нового о комплексных числах. Вот результат моей работы над этой темой.
Моей целью являлось изучение комплексных чисел как раздела математики, а также создание наглядного электронного пособия для учащихся старших классов и студентов первого курса технических ВУЗов.
Я считаю, что моя тема актуальна, так как хотя в наше время довольно много научной и учебной литературы, но далеко не во всех изданиях материал изложен ясно, понятно и доступно для учащихся.
Задача, которую я ставил перед собой, – проведение мониторинга (исследования) по изучению темы "Комплексные числа" по данному учебному пособию среди учащихся 11 класса.
2
ИСТОРИЯ РАЗВИТИЯ УЧЕНИЯ О КОМПЛЕКСНЫХ ЧИСЛАХ
Для решения алгебраических уравнений недостаточно действительных чисел. Поэтому естественно стремление сделать эти уравнения разрешимыми, что в свою очередь приводит к расширению понятия числа. Например, для того чтобы любое уравнение х + a = b имело корни, положительных чисел недостаточно и поэтому возникает потребность ввести отрицательные числа и нуль.
Древнегреческие математики считали, что, a = с и b = a только натуральные числа, но в практических расчетах за два тысячелетия до нашей эры в Древнем Египте и Древнем Вавилоне уже применялись дроби. Следующим важным этапом в развитии понятия о числе было введение отрицательных чисел – это было сделано китайскими математиками за 2 века до нашей эры. Отрицательные числа применял в III веке нашей эры древнегреческий математик Диофант, знавший уже правила действий над ними, а в VII веке нашей эры эти числа подробно изучили индийские ученые, которые сравнивали такие числа с долгом. С помощью отрицательных чисел можно было единым образом описывать изменение величин. Уже в VIII веке нашей эры было установлено, что квадратный корень из положительного числа имеет два значение – положительное и отрицательное, а из отрицательных чисел квадратные корни извлечь нельзя: нет такого числа х, чтобы х2
= - 9. В XVI веке в связи с изучением кубических уравнений оказалось необходимым извлекать квадратные корни из отрицательных чисел. В формуле для решения кубических уравнений содержатся кубические и квадратные корни. Эта формула безотказно действует в случае, когда уравнение имеет один действительный корень (например, для уравнения х3
+ 3х – 4 = 0), а если оно имело 3 действительных корня (например, х3
– 7х + 6 = 0),то под знаком квадратного корня оказывалось отрицательное число. Получалось, что путь к этим 3 корням уравнения ведет через невозможную операцию извлечения квадратного корня из отрицательного числа.
Чтобы объяснить получившийся парадокс, итальянский алгебраист Джироламо Кардано в 1545 г. предложил ввести числа новой природы. Он показал, что система уравнений х + у = 10, xy = 40 не имеющая решений во множестве действительных чисел, имеет решение всегда х = 5 ±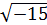 , у = 5 ± , у = 5 ±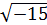 , нужно только условиться действовать над такими выражениями по правилам обычной алгебры и считать, что , нужно только условиться действовать над такими выражениями по правилам обычной алгебры и считать, что 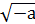 ∙ ∙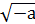 = -
a. Кардано называл такие величины «чисто отрицательными» и даже «софистически отрицательными», считая их бесполезными, и стремился не применять их. В самом деле, с помощью таких чисел нельзя выразить ни результат измерения какой-нибудь величины, ни изменение этой величины. Но уже в 1572 г. вышла книга итальянского алгебраиста Р. Бомбелли, в которой были установлены первые правила арифметических операций над такими числами, вплоть до извлечения из них кубических корней. Название «мнимые числа» ввел в 1637 г. французский математик и философ Р. Декарт, а в 1777 г. один из крупнейших математиков XVIII века Л. Эйлер предложил использовать первую букву французского слова imaginaire («мнимый») для обозначения = -
a. Кардано называл такие величины «чисто отрицательными» и даже «софистически отрицательными», считая их бесполезными, и стремился не применять их. В самом деле, с помощью таких чисел нельзя выразить ни результат измерения какой-нибудь величины, ни изменение этой величины. Но уже в 1572 г. вышла книга итальянского алгебраиста Р. Бомбелли, в которой были установлены первые правила арифметических операций над такими числами, вплоть до извлечения из них кубических корней. Название «мнимые числа» ввел в 1637 г. французский математик и философ Р. Декарт, а в 1777 г. один из крупнейших математиков XVIII века Л. Эйлер предложил использовать первую букву французского слова imaginaire («мнимый») для обозначения 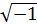 (мнимой единицы)
, т.е. i
= (мнимой единицы)
, т.е. i
= 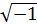 , этот символ вошел во всеобщее употребление благодаря К. Гауссу (1831 г). , этот символ вошел во всеобщее употребление благодаря К. Гауссу (1831 г).
В течение XVII века продолжалось обсуждение арифметической природы мнимостей, возможности дать им геометрическое истолкование. Постепенно развивалась техника операций над комплексными числами. На рубеже XVII – XVIII веков была построена общая теория корней n
-й степени сначала из отрицательных, а впоследствии и из любых комплексных чисел.
В конце XVIII века французский математик Ж. Лагранж смог сказать, что математический анализ уже не затрудняют мнимые величины. С помощью комплексных чисел научились выражать решения линейных дифференциальных уравнений с постоянным коэффициентом. Такие уравнения встречаются, например, в теории колебаний материальной точки в сопротивляющейся среде.
Я. Бернулли применил комплексные числа для вычисления интегралов. Хотя в течение XVIII века с помощью комплексных чисел были решены многие вопросы, в том числе и прикладные задачи, связанные с картографией, гидродинамикой и т. д., однако еще не было строго логического обоснования теории этих чисел. Поэтому французский ученый П. Лаплас считал, что результаты, получаемые с помощью мнимых чисел, - только наведение, приобретающие характер настоящих истин лишь после подтверждения прямыми доказательствами. В конце XVIII – начале XIX веков было получено геометрическое истолкование комплексных чисел. Датчанин Г. Вессель, француз Ж. Арган и немец К. Гаусс независимо друг от друга предложили изображать комплексное число z = a + bi точкой М (a, b) на координатной плоскости. Позднее оказалось, что еще удобнее изображать число не самой точкой М, а вектором ОМ, идущим в эту точку из начала координат. При таком истолковании сложению и вычитанию комплексных чисел соответствуют эти же операции над векторами.
Геометрические истолкования комплексных чисел позволили определить многие понятия, связанные с функциями комплексного переменного, расширило область их применения. Стало ясно, что комплексные числа полезны во многих вопросах, где имеют дело с величинами, которые изображаются векторами на плоскости: при изучении течения жидкости, задач теории упругости, в теоретической электротехнике.
Большой вклад в развитие теории функций комплексной переменной внесли русские и советские ученые: Р.И. Мусхелишвили занимался ее приложениями к теории упругости, М.В. Келдыш и М.А. Лаврентьев – к аэродинамике и гидродинамике, Н. Н. Боголюбов и В.С. Владимиров – к проблемам квантовой теории поля.
3
ДЕЙСТВИЯ С КОМПЛЕКСНЫМИ ЧИСЛАМИ
Я рассмотрел решение квадратного уравнения х2
+ 1 = 0. Отсюда х2
= –1. Число х, квадрат которого равен –1, называется мнимой единицей и обозначается i. Таким образом, i2
= -1, откуда i =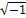 . Решение квадратного уравнения, например, х2
– 8х + 25 = 0, можно записать следующим образом: х = . Решение квадратного уравнения, например, х2
– 8х + 25 = 0, можно записать следующим образом: х =
= 4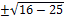 = 4 = 4 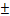 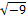 = 4 ± = 4 ± 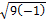 = 4 = 4 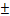 3 3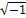 = 4 ± 3i. = 4 ± 3i.
Числа вида 4 + 3i и 4 – 3i называют комплексными числами. В общем виде комплексное число записывается a + bi, где a и b – действительные числа, а i – мнимая единица. Число a
называется действительной частью комплексного числа (Re, от фр. réele – «реальный», «действительный»), bi
– мнимой частью этого числа (Im, от фр. imaginaire – «мнимый»), b
–
коэффициентом мнимой части комплексного числа.
Комплексные числа равны, если равны их действительные части и коэффициенты мнимых частей: a + bi = c + di, если a = c, b = d. Комплексное число равно нулю тогда, когда его действительная часть и коэффициент мнимой части равны нулю, т.е. z = a + bi = 0, если a = 0, b = 0. Действительные числа являются частным случаем комплексных чисел. Если b = 0, то a + bi = a – действительное число. Если a = 0, b ≠ 0, то a + bi = bi – чисто мнимое число. Также на множестве комплексных чисел теряются понятия "больше" и "меньше", можно лишь по отдельности сравнивать действительные и мнимые части комплексных чисел.
Комплексно-сопряжённые числа.
 Сопряжёнными числами называют числа, действительные части которых равны, а мнимые отличаются знаком. Сопряжённое комплексному числу z обозначают z. Сопряжёнными числами называют числа, действительные части которых равны, а мнимые отличаются знаком. Сопряжённое комплексному числу z обозначают z.
Произведением и суммой сопряжённых чисел являются действительные числа:
(a + bi) + (a – bi) = 2a,
(a + bi) ∙ (a – bi) = a2
+ b2
.
Позже, когда была предложена геометрическая интерпретация комплексных чисел, возникла необходимость введения нового понятия – длины вектора, соответствующего комплексному числу. Его стали называть модулем комплексного числа и обозначать:
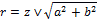
по предложению швейцарского математика Жана Аргана.
Самостоятельно изучив пример 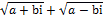 , я пришёл к выводу, что и сумма корней двух сопряжённых чисел равна действительному числу. Действительно, обозначив конечный результат за x
и учитывая, что обе части неотрицательны, я имею право возвести выражение в квадрат: , я пришёл к выводу, что и сумма корней двух сопряжённых чисел равна действительному числу. Действительно, обозначив конечный результат за x
и учитывая, что обе части неотрицательны, я имею право возвести выражение в квадрат:
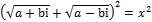
Раскрыв скобки и выполнив возможные действия в левой части, я получил:
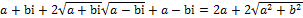 . Т.е. . Т.е. 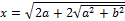
Так как a
и b
– действительные числа, то и это выражение будет действительным. Я доказал это на примере:
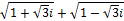 . Возведя в квадрат, я получил: . Возведя в квадрат, я получил:
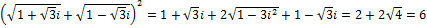 . .
Т.е. 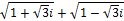 = =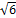 . .
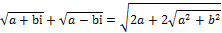
Сложение комплексных чисел.
Суммой двух комплексных чисел z1
= a + bi и z2
= c + di называется комплексное число z = (a + c) + (b + d)i. Для комплексных чисел справедливы переместительный и сочетательный законы сложения. Их справедливость следует из того, что сложение комплексных чисел по существу сводится к сложению действительных частей и коэффициентов мнимых частей, а они являются действительными числами, для которых справедливы указанные законы.
Вычитание комплексных чисел
определяется как действие, обратное сложению: разностью двух комплексных чисел a + bi и c + di называется комплексное число х + yi, которое в сумме с вычитаемым дает уменьшаемое. Отсюда, исходя из определения сложения и равенства комплексных чисел, получим два уравнения, из которых найдем, что х = a – c, у = b – d. Значит,
(a + bi) – (c + di) = (a – c) + (b – d)i.
Произведение
комплексных
чисел
z1
= a + bi и z2
= c + di называется комплексное число z = (ac – bd) + (ad + bc)i, z1
z2
= (a + bi) ∙ (c + di) = (ac – bd) + + (ad + bc) i. Легко проверить, что умножение комплексных чисел можно выполнять как умножение многочленов с заменой i2
на –1. Для умножения комплексных чисел также справедливы переместительный и сочетательный законы, а также распределительный закон умножения по отношению к сложению.
Деление комплексных чисел,
кроме деления на нуль, определяется как действие, обратное умножению. Конкретное правило деления получим, записав частное в виде дроби и умножив числитель и знаменатель этой дроби на число, сопряженное со знаменателем:
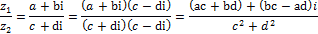
Или короче: 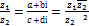 . .
Степень числа
i
является периодической функцией с периодом 4. Я доказал это утверждение: i3
= i2
∙ i = (– 1) i = – i; i4
= i3
∙ i = (– i) i = – i2
= – (– 1) = 1; i5
=
= i4
∙ i = 1 ∙ i = i; i6
= i5
∙ i = i ∙ i = – 1. Вообще, i4n + k
= (i4
)n
∙ ik
= 1n
∙ ik
.
4
РЕШЕНИЕ УРАВНЕНИЙ С КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
Сначала я рассмотрел простейшее квадратное уравнение z2
= a, где a – заданное число, z – неизвестное. На множестве действительных чисел это уравнение:
1) имеет один корень z = 0, если a = 0;
2) имеет два действительных корня z1,2
= ±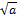 , если a > 0; , если a > 0;
3) не имеет действительных корней, если a < 0;
4) на множестве комплексных чисел это уравнение всегда имеет корень.
Вообще уравнение
z
2
=
a
, где
a
< 0 имеет два комплексных корня:
z
1,2
=±
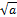 i
. i
.
Используя равенство i2
= –1, квадратные корни из отрицательных чисел принято записывать так: 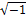 = i, = i, 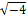 = i = i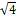 = 2i, = 2i, 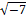 = i = i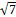 . .
Итак, 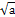 определен для любого действительного числа a (положительного, отрицательного и нуля). Поэтому любое квадратное уравнение определен для любого действительного числа a (положительного, отрицательного и нуля). Поэтому любое квадратное уравнение
az2
+ bz + c = 0, где a, b, с – действительные числа, a ≠ 0, имеет корни. Эти корни находятся по известной формуле:
z1, 2
=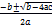 . .
Также справедливо утверждение, что любое уравнение степени n
имеет ровно n
корней, при этом среди них могут быть одинаковые и комплексные.
Невозможно не рассмотреть одну из красивейших формул математики – формулу Кардано для вычисления корней кубического уравнения вида x3
+ px + q = 0:
 . .
По видимому, эту же формулу ранее получили Сцепион дель Ферро и Николо Фонтане (Тарталья), но первым опубликовал эту формулу именно Кардано.
5
ГЕОМЕТРИЯ КОМПЛЕКСНЫХ ЧИСЕЛ
Наглядно представить мнимые числа пытались ещё в XVIII веке.
В 1799 г. датский математик Каспар Вессель предложил простую геометрическую интерпретацию комплексных чисел, однако его работа осталась незамеченной. В 1806 г. швейцарец Жан Агран высказал похожую идею. Но широкое распространение эта интерпретация получила лишь через три десятка лет, когда Карл Фридрих Гаусс выпустил в свет труд «Теория биквадратных вычетов», в котором дал такое же геометрическое изображение комплексных чисел, как Вессель и Агран. Больше всего меня поразило то, что практически одновременно, независимо друг от друга трое учёных предложили одну и ту же идею. Это говорит о том, что идея буквально витала в воздухе. Вообще, именно это открытие способствовало дальнейшему развитию учения о комплексных числах: стала возможна тригонометрическая запись числа, и, как следствие, намного удобнее стали возведение в степень и извлечение корня.
Точками на числовой оси можно представлять как действительные, так и мнимые числа (но только не на одной и той же оси). Значит, чтобы одновременно изобразить действительные и мнимые числа нужно взять сразу две оси. Назовём их действительной осью и мнимой осью и расположим перпендикулярно. Для определённости выберем положительное направление действительной оси вправо, а мнимой – вверх.
Теперь можно наглядно представить операции сложения и вычитания комплексных чисел с помощью векторов.
Аргумент комплексного числа.
Когда я изображал комплексно-сопряжённые числа как вектора, возникла неопределённость, так как углы между соответствующими сопряжённым числам векторами равны. Во избежание этой неопределённости необходимо ввести понятие направления измерения угла и как следствие – отрицательные углы. Направление от положительной полуоси против часовой стрелки значение угла принято считать положительным, а против – отрицательным. Этот угол называют аргументом комплексного числа и обозначают так: φ = arg z. Обычно он измеряется не в градусах, а в радианах. Но и аргумент не полностью устраняет неопределённость. Выходит, если φ – аргумент комплексного числа, то и φ + 2πk (k = 0, ±1, ±2, …). Но эту неопределённость устранять не стоит (она понадобилась мне для извлечения корня из комплексного числа).
Модуль комплексного числа.
Я заметил одну интересную закономерность. Если каждое действительное число имеет только одно число с таким же модулем, то комплексные числа имеют бесконечное множество чисел с одинаковым модулем. Действительно, если взять точку M, соответствующую числу z = a + bi на координатной плоскости, провести к ней радиус-вектор, а потом провести окружность радиуса |z| = 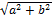 с центром в точке O, то будет видно, что все числа, имеющие такой же модуль |z| = с центром в точке O, то будет видно, что все числа, имеющие такой же модуль |z| =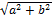 , будут лежать на этой окружности. , будут лежать на этой окружности.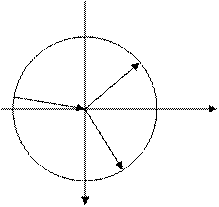
Тригонометрическая форма записи комплексных чисел.

Я взял произвольное комплексное число z = a + bi и изобразил его в виде радиус-вектора 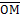 на комплексной плоскости. Пусть N – проекция точки M на действительную ось. В прямоугольном треугольнике OMN длины катетов ON и OM равны соответственно a и b, а длина гипотенузы OM равна на комплексной плоскости. Пусть N – проекция точки M на действительную ось. В прямоугольном треугольнике OMN длины катетов ON и OM равны соответственно a и b, а длина гипотенузы OM равна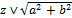 . Из тригонометрии известно, что отношение длины катета к длине гипотенузы равняется косинусу прилежащего угла и синусу противолежащего. Следовательно, . Из тригонометрии известно, что отношение длины катета к длине гипотенузы равняется косинусу прилежащего угла и синусу противолежащего. Следовательно,
a = Re z = | z | ∙ cos φ,
b = Im z = | z | ∙ sin φ,
где φ – аргумент комплексного числа z. Таким образом,
z = a + bi = | z | ∙ cos φ + | z | ∙ sin φ ∙ i = |
z
| ∙ (
cos
φ
+
i
sin
φ
)
.
Произведение двух комплексных чисел z1
= | z1
| ∙ (cos φ1
+ i sin φ1
) и
z2
= | z2
| ∙ (cos φ2
+ i sin φ2
) будет равно:
z1
∙ z2
= | z1
| | z2
| (cos φ1
+ i sin φ1
) (cos φ2
+ i sin φ2
) =
= | z1
| | z2
| ((cos φ1
cos φ2
– sin φ1
sin φ2
) + i (sin φ1
cos φ2
+ cos φ1
sin φ2
)) =
= | z1
| | z2
| (cos (φ1
+ φ2
) + i sin (φ1
+ φ2
)).
При умножении комплексных чисел их модули необходимо перемножить, а аргументы – сложить.
При делении необходимо произвести обратные операции: поделить модули и вычесть аргументы.
6
ВОЗВЕДЕНИЕ В СТЕПЕНЬ И ИЗВЛЕЧЕНИЕ КОРНЯ ИЗ КОМПЛЕКСНОГО
ЧИСЛА
Я возвёл комплексное число z = r ∙ (cos φ + i sin φ) в степень n:
zn
= rn
(cos nφ + i sin nφ).
Это выражение назвали формулой Муавра – в честь английского математика Абрахама де Муавра, открывшего её в 1701 г.
При n = 1, я получил zn
= rn
(cosφ + i sinφ)n
= rn
(cos nφ + i sin nφ).
То есть rn
(cosφ + i sinφ)n
= rn
(cos nφ + i sin nφ), или, если разделить на rn
≠ 0: (cosφ + i sinφ)n
= (cos nφ + i sin nφ).
Этой формулой можно воспользоваться для выражения синусов и косинусов аргумента nφ через синусы и косинусы аргумента φ. Для этого я применил к левой части формулу бинома Ньютона и учёл формулы для степеней числа i. Получается, что
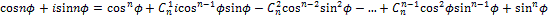
Отсюда следуют равенства
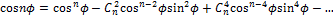
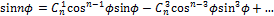
Суммирование ведётся до тех пор, пока показатель при cos φ не обратится в 0 или в 1 (в зависимости от чётности n). Поскольку в выражение для cos nφ входят лишь чётные степени sin φ, то их можно выразить лишь через cos φ. Для sin nφ при нечётном n можно получить выражение лишь через sin φ, а при чётном n – в виде произведения cos φ на выражение от sinφ.
Извлечение корня из комплексного числа.
Как и для действительных чисел, корнем n-й степени из комплексного числа z, где n – натуральное число, называют такое комплексное число w, что wn
= z. Корень n-й степени из z обозначают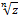 . Я приведу доказательство, что из любого комплексного числа z можно извлечь корень n-й степени, причём если z ≠ 0, то . Я приведу доказательство, что из любого комплексного числа z можно извлечь корень n-й степени, причём если z ≠ 0, то 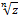 принимает n различных значений. принимает n различных значений.
Я записывал числа в тригонометрической форме.
Пусть z = r (cos φ1
+ i sin φ1
). Число w я искал в виде w = R (cos φ2
+ i sin φ2
). Равенство wn
= z принимает вид:
Rn
(cos nφ2
+ i sin nφ2
) = r (cos φ1
+ i sin φ1
).
Но два комплексных числа равны тогда и только тогда, когда их модули равны, а аргументы отличаются лишь слагаемым, кратным 2π. Значит,
Rn
= r,
nφ = φ + 2πk, kZ.
итак, для модуля R искомого числа я получил определённое значение. Что же касается аргумента φ этого числа, он может принимать различные значения в зависимости от значения числа k. Я выяснил, при каких значениях k1
и k2
получаются значения φ, отличающиеся друг от друга на кратное 2π (т. е. одинаковые значения w). Для этого разность
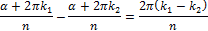
должна быть кратна 2π. Это имеет место тогда и только тогда, когда k1
– k2
делится на n. Отсюда следует, что при r ≠ 0 значениям k = 0, 1, …, n – 1 соответствуют различные значения корня, а k = n даёт то же значение корня, что и при k = 1 и т. д. Число различных значений корня равно n.
Таким образом, я доказал утверждение:
Теорема.
Для любого натурального числа n и любого отличного от нуля комплексного числа z существуют n различных значений корня n-й степени.
Если z = r (cos φ + i sin φ), то эти значения выражаются формулой
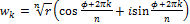 , ,
где k = 0, 1, …, n – 1.
Все точки wk
лежат на окружности радиусом 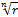 с центром в начале координат. Аргументы соседних точек отличаются на с центром в начале координат. Аргументы соседних точек отличаются на 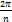 , а потому указанные точки делят окружность на n равных частей. Иными словами, они являются вершинами правильного n-угольника, вписанного в эту окружность. , а потому указанные точки делят окружность на n равных частей. Иными словами, они являются вершинами правильного n-угольника, вписанного в эту окружность.
7
ЗАКЛЮЧЕНИЕ
В общем, я считаю, что цель и задача моего проекта выполнены. Я сам освоил тему и создал наглядное пособие, чтобы облегчить учащимся её изучение и проверку усвоения материала. В ходе исследования я изучил много литературы по данной теме, общался с научным работником, который занимается этой темой профессионально и т.д. В ходе чтения разных книг я отметил для себя наиболее интересные, простые и красивые доказательства теорем по этой теме, одновременно стараясь изложить их в своём свете, так, как я считаю наиболее рациональным.
К достоинствам моего учебника можно отнести краткость и простоту изложения, объединение знаний о комплексных числах воедино, доступность.
Я считаю мой учебник полезным и актуальным для тех учеников, которые хотят узнать больше школьной программы, для тех из них, кто планирует учиться в техническом ВУЗе и в дальнейшем работать по технической специальности.
В ходе исследования я провёл элективный курс для учащихся 11 Б класса прошлого года (25 человек) из 5 занятий и после этого проверил успеваемость и степень усвоения материала. Результат можно видеть на диаграмме: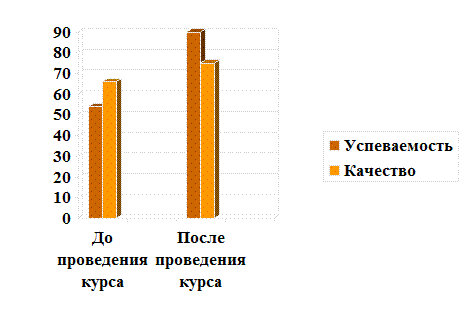
Из программы средней школы тема "Комплексные числа" исключена, но в гимназии существует элективный курс "Дискретная математика", составной частью которого являются комплексные числа. Моё пособие будет хорошим подспорьем учителям в ходе преподавания, а также всем желающим самостоятельно изучить данный раздел математики.
8
СПИСОК ЛИТЕРАТУРЫ
1. Математика. Энциклопедия для детей под редакцией М. Д. Аксёновой. – Москва-2000.
2. Алгебра и математический анализ для 11 класса под редакцией Н. Я. Виленкина. – Москва-1996.
3. История математики в школе под редакцией Г. И. Глейзер. – Москва-1983.
4. Избранные вопросы математики под редакцией И. Н. Антипова. – Москва-1979.
5. За страницами учебника математики под редакцией Н. Я. Виленкина. - Москва-1996.
|