|
Вопросы к экзамену по дисциплине
«Математика для экономистов»
блок «Высшая математика».
1.
Понятие матриц. Виды матриц.
Определение.
Матрицей
размера m´n, где m- число строк, n- число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются aij
, где i- номер строки, а j- номер столбца.
А = 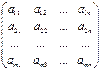
Основные действия над матрицами.
Матрица может состоять как из одной строки, так и из одного столбца. Вообще говоря, матрица может состоять даже из одного элемента.
Определение.
Если число столбцов матрицы равно числу строк (m=n), то матрица называется квадратной
.
Определение.
Матрица вида:
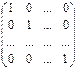 = E
, = E
,
называется
единичной матрицей
.
Определение.
Если amn
=
anm
, то матрица называется
симметрической
.
Пример
.
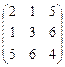 - симметрическая матрица - симметрическая матрица
Определение.
Квадратная матрица вида 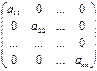 называется диагональной
матрицей. называется диагональной
матрицей.
2.
Линейные операции над матрицами.
Сложение и вычитание
матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что они определены только для матриц одинакового размера
. Таким образом, возможно определить операции сложения и вычитания матриц:
Определение.
Суммой (разностью)
матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.
cij
= aij
± bij
С = А + В = В + А.
Операция умножения (деления)
матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число.
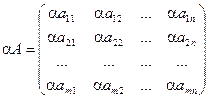
a (А+В) =aА ± aВ
А(a±b) = aА ± bА
Пример.
Даны матрицы А = 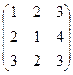 ; B = ; B = 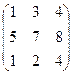 , найти 2А + В. , найти 2А + В.
2А = 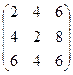 , 2А + В = , 2А + В = 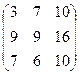 . .
Операция умножения матриц
.
Определение:
Произведением
матриц называется матрица, элементы которой могут быть вычислены по следующим формулам:
A×B = C;
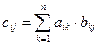 . .
Из приведенного определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй.
Свойства операции умножения матриц.
1)Умножение матриц не коммутативно
, т.е. АВ ¹ ВА даже если определены оба произведения. Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными.
Самым характерным примером может служить единичная
матрица, которая является перестановочной с любой другой матрицей того же размера.
Перестановочными могут быть только квадратные матрицы одного и того же порядка.
А×Е = Е×А = А
Очевидно, что для любых матриц выполняются следующее свойство:
A×O = O; O×A = O,
где О – нулевая
матрица.
2) Операция перемножения матриц ассоциативна,
т.е. если определены произведения АВ и (АВ)С, то определены ВС и А(ВС), и выполняется равенство:
(АВ)С=А(ВС).
3) Операция умножения матриц дистрибутивна
по отношению к сложению, т.е. если имеют смысл выражения А(В+С) и (А+В)С, то соответственно:
А(В + С) = АВ + АС
(А + В)С = АС + ВС.
4) Если произведение АВ определено, то для любого числа a верно соотношение:
a(AB) = (aA)B = A(aB).
5) Если определено произведение АВ , то определено произведение ВТ
АТ
и выполняется равенство:
(АВ)Т
= ВТ
АТ
, где
индексом Т обозначается транспонированная
матрица.
6) Заметим также, что для любых квадратных матриц det (AB) = detA×detB.
Понятие det (определитель, детерминант) будет рассмотрено ниже.
Определение
.
Матрицу В называют транспонированной
матрицей А, а переход от А к В транспонированием
, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы В.
А = 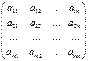 ; В = АТ
= ; В = АТ
=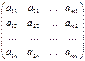 ; ;
другими словами, bji
= aij
.
В качестве следствия из предыдущего свойства (5) можно записать, что:
(ABC)T
= CT
BT
AT
,
при условии, что определено произведение матриц АВС.
Пример.
Даны матрицы А = 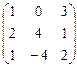 , В = , В = 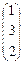 , С = , С =  и число a = 2. Найти АТ
В+aС. и число a = 2. Найти АТ
В+aС.
AT
= 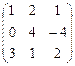 ; AT
B = ; AT
B = 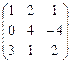 × ×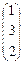 = = 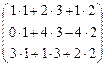 = = 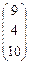 ; ;
aC = 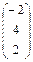 ; АТ
В+aС = ; АТ
В+aС = 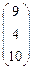 + +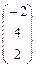 = = 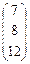 . .
Пример.
Найти произведение матриц А = 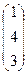 и В = и В = 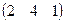 . .
АВ = 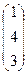 × ×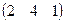 = = 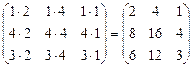 . .
ВА = 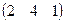 × ×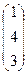 = 2×1 + 4×4 + 1×3 = 2 + 16 + 3 = 21. = 2×1 + 4×4 + 1×3 = 2 + 16 + 3 = 21.
Пример.
Найти произведение матриц А=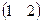 , В = , В = 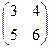
АВ = 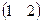 × ×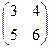 = = 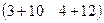 = =  . .
3.
Определители. Вычисление определителей.
Определителем
квадратной матрицы А=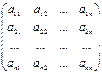 называется число, которое может быть вычислено по элементам матрицы по формуле: называется число, которое может быть вычислено по элементам матрицы по формуле:
det A = 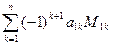 , где , где
М1к
– детерминант матрицы, полученной из исходной вычеркиванием первой строки и k – го столбца. Следует обратить внимание на то, что определители имеют только квадратные матрицы, т.е. матрицы, у которых число строк равно числу столбцов.
Предыдущая формула позволяет вычислить определитель матрицы по первой строке, также справедлива формула вычисления определителя по первому столбцу:
det A = 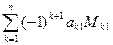
Вообще говоря, определитель может вычисляться по любой строке или столбцу матрицы, т.е. справедлива формула:
detA = 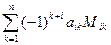 , i = 1,2,…,n. , i = 1,2,…,n.
Очевидно, что различные матрицы могут иметь одинаковые определители.
Определитель единичной матрицы равен 1.
Для указанной матрицы А число М1к
называется дополнительным минором
элемента матрицы a1
k
. Таким образом, можно заключить, что каждый элемент матрицы имеет свой дополнительный минор. Дополнительные миноры существуют только в квадратных матрицах.
Определение.
Дополнительный минор
произвольного элемента квадратной матрицы aij
равен определителю матрицы, полученной из исходной вычеркиванием i-ой строки и j-го столбца.
4.
Определители. Свойства определителей.
Свойство1.
Важным свойством определителей является следующее соотношение:
det A = det AT
;
Свойство
2.
det (AB) = detA×detB
Свойство
3.
Если в квадратной матрице поменять местами какие-либо две строки (или столбца), то определитель матрицы изменит знак, не изменившись по абсолютной величине.
Свойство 4.
При умножении столбца (или строки) матрицы на число ее определитель умножается на это число.
Определение:
Столбцы (строки) матрицы называются линейно зависимыми
, если существует их линейная комбинация, равная нулю, имеющая нетривиальные (не равные нулю) решения.
Свойство 6.
Если в матрице А строки или столбцы линейно зависимы, то ее определитель равен нулю.
Свойство 7.
Если матрица содержит нулевой столбец или нулевую строку, то ее определитель равен нулю. (Данное утверждение очевидно, т.к. считать определитель можно именно по нулевой строке или столбцу.)
Свойство 8.
Определитель матрицы не изменится, если к элементам одной из его строк(столбца) прибавить(вычесть) элементы другой строки(столбца), умноженные на какое-либо число, не равное нулю.
Свойство 9.
Если для элементов какой- либо строки или столбца матрицы верно соотношение: d
=
d
1
±
d
2
,
e
=
e
1
±
e
2
,
f
=
f
1
±
f
2
,
то верно:
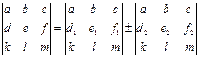
Пример.
Вычислить определитель матрицы А = 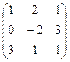
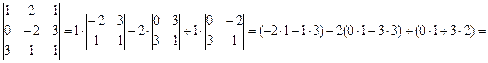
= -5 + 18 + 6 = 19.
Пример:
. Даны матрицы А = 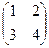 , В = , В = 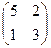 . Найти det (AB). . Найти det (AB).
1-й способ: det A = 4 – 6 = -2; det B = 15 – 2 = 13; det (AB) = det A ×det B = -26.
2- й способ: AB = 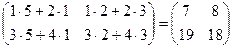 , det (AB) = 7×18 - 8×19 = 126 – , det (AB) = 7×18 - 8×19 = 126 –
– 152 = -26.
5.
Обратная матрица.
Определим операцию деления матриц как операцию, обратную умножению.
Определение.
Если существуют квадратные матрицы Х и А одного порядка, удовлетворяющие условию:
XA = AX = E,
где Е - единичная матрица того же самого порядка, что и матрица А, то матрица Х называется обратной
к матрице А и обозначается А-1
.
Каждая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом только одну.
Рассмотрим общий подход к нахождению обратной матрицы.
Исходя из определения произведения матриц, можно записать:
AX = E Þ 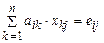 , i=(1,n), j=(1,n), , i=(1,n), j=(1,n),
eij
= 0, i ¹ j,
eij
= 1, i = j .
Таким образом, получаем систему уравнений:
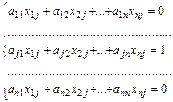 , ,
Решив эту систему, находим элементы матрицы Х.
Пример.
Дана матрица А = 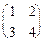 , найти А-1
. , найти А-1
.
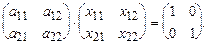
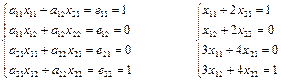 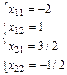
Таким образом, А-1
=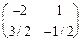 . .
Однако, такой способ не удобен при нахождении обратных матриц больших порядков, поэтому обычно применяют следующую формулу:
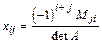 , ,
где Мji
- дополнительный минор
элемента аji
матрицы А.
Пример.
Дана матрица А = 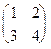 , найти А-1
. , найти А-1
.
det A = 4 - 6 = -2.
M11
=4; M12
= 3; M21
= 2; M22
=1
x11
= -2; x12
= 1; x21
= 3/2; x22
= -1/2
Таким образом, А-1
=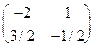 . .
6.
Решение систем линейных уравнений по формулам Крамера.
(Габриель Крамер (1704-1752) швейцарский математик)
Данный метод применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений. Кроме того, необходимо ввести ограничения на коэффициенты системы. Необходимо, чтобы все уравнения были линейно независимы, т.е. ни одно уравнение не являлось бы линейной комбинацией остальных.
Для этого необходимо, чтобы определитель матрицы системы не равнялся 0.
det A ¹ 0;
Действительно, если какое- либо уравнение системы есть линейная комбинация остальных, то если к элементам какой- либо строки прибавить элементы другой, умноженные на какое- либо число, с помощью линейных преобразований можно получить нулевую строку. Определитель в этом случае будет равен нулю.
Теорема. (Правило Крамера):
Теорема.
Система из
n
уравнений с
n
неизвестными
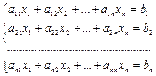
в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:
xi
=
D
i
/
D
, где
D
=
det
A
, а
D
i
– определитель матрицы, получаемой из матрицы системы заменой столбца
i
столбцом свободных членов
bi
.
D
i
= 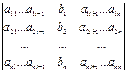
Пример
.
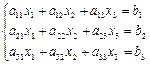
A = 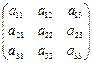 ; D1
= ; D1
= 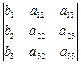 ; D2
= ; D2
= 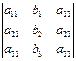 ; D3
= ; D3
= 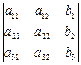 ; ;
x1
= D1
/detA; x2
= D2
/detA; x3
= D3
/detA;
Пример.
Найти решение системы уравнений:
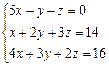
D =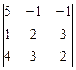 = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30; = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
D1
= 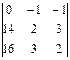 = (28 – 48) – (42 – 32) = -20 – 10 = -30. = (28 – 48) – (42 – 32) = -20 – 10 = -30.
x1
= D1
/D = 1;
D2
= 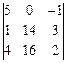 = 5(28 – 48) – (16 – 56) = -100 + 40 = -60. = 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
x2
= D2
/D = 2;
D3
= 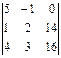 = 5( 32 – 42) + (16 – 56) = -50 – 40 = -90. = 5( 32 – 42) + (16 – 56) = -50 – 40 = -90.
x3
= D3
/D = 3.
Как видно, результат совпадает с результатом, полученным выше
матричным методом.
Если система однородна, т.е. bi
= 0, то при D¹0 система имеет единственное нулевое решение x1
= x2
= … = xn
= 0.
При в = 0 система имеет бесконечное множество решений.
Для самостоятельного решения:
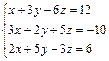 ; Ответ:
x
= 0;
y
= 0;
z
= -2. ; Ответ:
x
= 0;
y
= 0;
z
= -2.
7.
Решение систем линейных уравнений с помощью обратной матрицы.
Матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных.
Метод удобен для решения систем невысокого порядка.
Метод основан на применении свойств умножения матриц.
Пусть дана система уравнений:
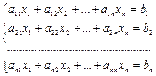
Составим матрицы: A = 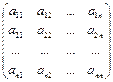 ; B = ; B = 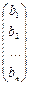 ; X = ; X = 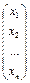 . .
Систему уравнений можно записать:
A×X = B.
Сделаем следующее преобразование: A-1
×A×X = A-1
×B,
т.к. А-1
×А = Е, то Е×Х = А-1
×В
Х = А-1
×
В
Для применения данного метода необходимо находить обратную матрицу
, что может быть связано с вычислительными трудностями при решении систем высокого порядка.
Пример
.
Решить систему уравнений:
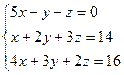
Х = 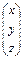 , B = , B = 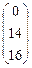 , A = , A = 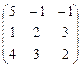
Найдем обратную матрицу А-1
.
D = det A = 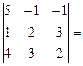 5(4-9) + 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30. 5(4-9) + 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30.
M11
= 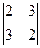 = -5; M21
= = -5; M21
= 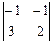 = 1; M31
= = 1; M31
= 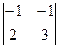 = -1; = -1;
M12
= 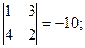 M22
= M22
= 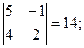 M32
= M32
= 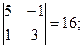
M13
= 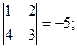 M23
= M23
= 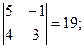 M33
= M33
= 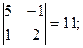
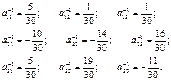 A-1
= A-1
= 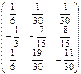 ; ;
Cделаем проверку:
A×A-1
= 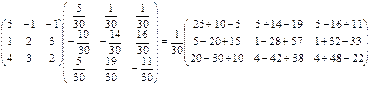 =E. =E.
Находим матрицу Х.
Х = 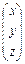 = А-1
В = = А-1
В = 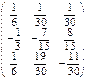 × ×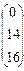 = = 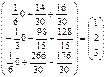 . .
Итого решения системы:
x =1; y = 2; z = 3.
Несмотря на ограничения возможности применения данного метода и сложность вычислений при больших значениях коэффициентов, а также систем высокого порядка, метод может быть легко реализован на ЭВМ.
8.
Понятие векторов и действия над ними.
Определение.
Вектором
называется направленный отрезок (упорядоченная пара точек). К векторам относится также и нулевой
вектор, начало и конец которого совпадают.
Определение.
Длиной (модулем)
вектора называется расстояние между началом и концом вектора.
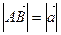
Определение
.
Векторы называются коллинеарными
, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору.
Определение.
Векторы называются компланарными
, если существует плоскость, которой они параллельны.
Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны.
Определение.
Векторы называются равными
, если они коллинеарны, одинаково направлены и имеют одинаковые модули.
Всякие векторы можно привести к общему началу, т.е. построить векторы, соответственно равные данным и имеющие общее начало. Из определения равенства векторов следует, что любой вектор имеет бесконечно много векторов, равных ему.
Определение.
Линейными операциями
над векторами называется сложение и умножение на число.
Суммой векторов является вектор - 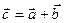
Произведение - 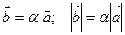 , при этом , при этом  коллинеарен коллинеарен  . .
Вектор  сонаправлен с вектором сонаправлен с вектором  ( (   ), если a > 0. ), если a > 0.
Вектор  противоположно направлен с вектором противоположно направлен с вектором  ( ( ¯ ¯ ), если a < 0. ), если a < 0.
9.
Скалярное произведение векторов. Угол между двумя векторами.
Определение.
Скалярным произведением
векторов  и и  называется число, равное произведению длин этих сторон на косинус угла между ними. называется число, равное произведению длин этих сторон на косинус угла между ними.
 × × = ï = ï ïï ïï ïcosj ïcosj
Свойства
скалярного произведения:
1)  × × = ï = ï ï2
; ï2
;
2)  × × = 0, если = 0, если  ^ ^ или или  = 0 или = 0 или  = 0. = 0.
3)  × × = =  × × ; ;
4)  ×( ×( + +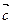 ) = ) =  × × + +  × ×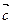 ; ;
5) (m )× )× = =  ×(m ×(m ) = m( ) = m( × × ); m=const ); m=const
Если рассматривать векторы 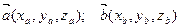 в декартовой прямоугольной системе координат, то в декартовой прямоугольной системе координат, то
 × × = xa
xb
+ ya
yb
+ za
zb
; = xa
xb
+ ya
yb
+ za
zb
;
Используя полученные равенства, получаем формулу для вычисления угла между векторами:
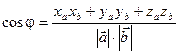 ; ;
Пример.
Найти (5 + 3 + 3 )(2 )(2 - -  ), если ), если 
10 × × - 5 - 5 × × + 6 + 6 × × - 3 - 3 × × = 10 = 10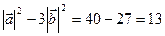 , ,
т.к. 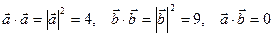 . .
Пример.
Найти угол между векторами  и и  , если , если 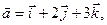
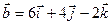 . .
Т.е.  = (1, 2, 3), = (1, 2, 3),  = (6, 4, -2) = (6, 4, -2)
 × × = 6 + 8 – 6 = 8: = 6 + 8 – 6 = 8:
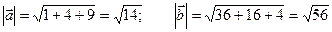 . .
cosj = 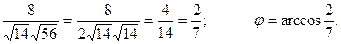
Пример.
Найти скалярное произведение (3 - 2 - 2 )×(5 )×(5 - 6 - 6 ), если ), если 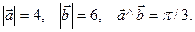
15 × × - 18 - 18 × × - 10 - 10 × × + 12 + 12 × × = 15 = 15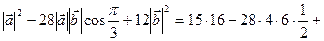
+ 12×36 = 240 – 336 + 432 = 672 – 336 = 336.
Пример.
Найти угол между векторами  и и  , если , если 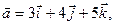
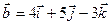 . .
Т.е.  = (3, 4, 5), = (3, 4, 5),  = (4, 5, -3) = (4, 5, -3)
 × × = 12 + 20 - 15 =17 : = 12 + 20 - 15 =17 :
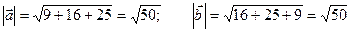 . .
cosj = 
Пример.
При каком m векторы 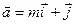 и и 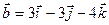 перпендикулярны. перпендикулярны.
 = (m, 1, 0); = (m, 1, 0);  = (3, -3, -4) = (3, -3, -4)
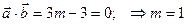 . .
Пример.
Найти скалярное произведение векторов 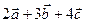 и и 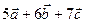 , если , если 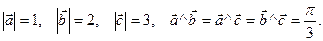
(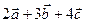 )( )(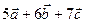 ) = ) = 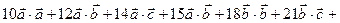
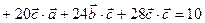 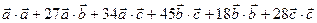 = 10 + = 10 +
+ 27 + 51 + 135 + 72 + 252 = 547.
10.
Координаты вектора. Действия над векторами, заданными своими координатами.
Определение.
1) Базисом
в пространстве называются любые 3 некомпланарных вектора, взятые в определенном порядке.
2) Базисом
на плоскости называются любые 2 неколлинеарные векторы, взятые в определенном порядке.
3)Базисом
на прямой называется любой ненулевой вектор.
Определение.
Если 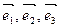 - базис в пространстве и - базис в пространстве и 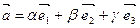 , то числа a, b и g - называются компонентами или координатами
вектора , то числа a, b и g - называются компонентами или координатами
вектора  в этом базисе. в этом базисе.
В связи с этим можно записать следующие свойства
:
- равные векторы имеют одинаковые координаты,
- при умножении вектора на число его компоненты тоже умножаются на это число,
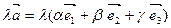 = = 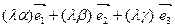 . .
- при сложении векторов складываются их соответствующие компоненты.
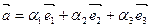 ; ; 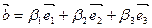 ; ;
 + +  = = 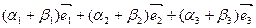 . .
Декартовой системой координат
в пространстве называется совокупность точки и базиса. Точка называется началом координат
. Прямые, проходящие через начало координат называются осями координат
.
1-я ось – ось абсцисс
2-я ось – ось ординат
3-я ось – ось апликат
Чтобы найти компоненты вектора нужно из координат его конца вычесть координаты начала.
Если заданы точки А(x1
, y1
, z1
), B(x2
, y2
, z2
), то 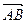 = (x2
– x1
, y2
– y1
, z2
– z1
). = (x2
– x1
, y2
– y1
, z2
– z1
).
Определение.
Базис называется ортонормированным
, если его векторы попарно ортогональны и равны единице.
Определение.
Декартова система координат, базис которой ортонормирован называется декартовой прямоугольной системой координат
.
Длина вектора в координатах
определяется как расстояние между точками начала и конца вектора. Если заданы две точки в пространстве А(х1
, y1
, z1
), B(x2
, y2
, z2
), то 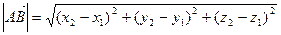 . .
Если точка М(х, у, z) делит отрезок АВ в соотношении
l
/
m
, считая от А, то координаты этой точки определяются как:
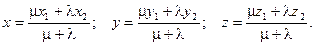
В частном случае координаты середины отрезка
находятся как:
x = (x1
+ x2
)/2; y = (y1
+ y2
)/2; z = (z1
+ z2
)/2.
Линейные
операции над векторами в координатах.
Пусть заданы векторы в прямоугольной системе координат
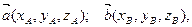 тогда линейные операции над ними в координатах имеют вид: тогда линейные операции над ними в координатах имеют вид:
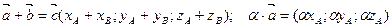
11.
Условия коллинеарности и ортогональности двух векторов.
Условие коллинеарности
двух векторов в коорднинатной форме.
векторы называются коллинеарными, если прямые параллельны или совпадают.
Два вектора коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны. Т.е. если 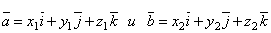 , то , то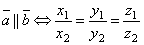 . .
Доказательство
:
Пусть вектор 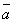 коллинеарен коллинеарен 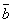 , тогда найдется λ такое, что , тогда найдется λ такое, что 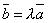 . Значит, . Значит, 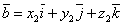 и и 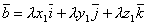 . Поскольку разложение вектора по элементам базиса . Поскольку разложение вектора по элементам базиса  единственно, то единственно, то 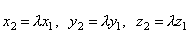 . .
Пусть выполняется равенство 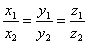 . Обозначим коэффициент пропорциональности через λ. Тогда . Обозначим коэффициент пропорциональности через λ. Тогда 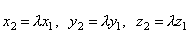 и, следовательно, и, следовательно, 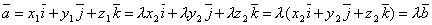 , т.е. , т.е. 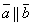 . Теорема доказана. . Теорема доказана.
Пример
.
Даны векторы 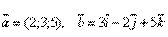 . Найти вектор . Найти вектор 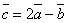 . .
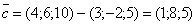 . .
Условие ортогональности
двух векторов:
Ортогональными
(перпендикулярными) называются векторы, скалярное произведение которых равно нулю.
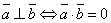 или или 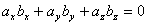 . .
Т.о., для того чтобы два вектора были перпендикулярны необходимо и достаточно, чтобы сумма произведений соответствующих координат этих векторов была равна нулю.
Примеры.
Пусть А
(-1; 1; 0), B
(3; 1; -2), 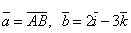 . Найти: . Найти:
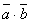 ; ;
 и и 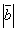 ; ;
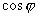 . .
a. 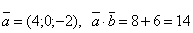 . .
b. 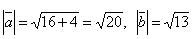 . .
c.  . .
12.
Уравнение прямой с угловым коэффициентом. Угол между прямыми. Условия параллельности и перпендикулярности прямых.
Как известно, любая точка на плоскости определяется двумя координатами в какой- либо системе координат. Системы координат могут быть различными в зависимости от выбора базиса и начала координат.
Определение.
Уравнением линии
называется соотношение y = f(x) между координатами точек, составляющих эту линию.
Отметим, что уравнение линии может быть выражено параметрическим способом, то есть каждая координата каждой точки выражается через некоторый независимый параметр t
.
Характерный пример – траектория движущейся точки. В этом случае роль параметра играет время.
Уравнение прямой на плоскости.
Определение.
Любая прямая на плоскости может быть задана уравнением первого порядка
Ах + Ву + С = 0,
причем постоянные А, В не равны нулю одновременно, т.е. А2
+ В2
¹ 0. Это уравнение первого порядка называют
общим уравнением прямой.
В зависимости от значений постоянных А,В и С возможны следующие частные случаи:
- C = 0, А ¹ 0, В ¹ 0 – прямая проходит через начало координат
- А = 0, В ¹ 0, С ¹ 0 { By + C = 0}- прямая параллельна оси Ох
- В = 0, А ¹ 0, С ¹ 0 { Ax + C = 0} – прямая параллельна оси Оу
- В = С = 0, А ¹ 0 – прямая совпадает с осью Оу
- А = С = 0, В ¹ 0 – прямая совпадает с осью Ох
Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.
Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:
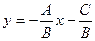
и обозначить 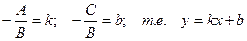 , то полученное уравнение называется уравнением прямой с угловым коэффициентом
k
. , то полученное уравнение называется уравнением прямой с угловым коэффициентом
k
.
Определение.
Если заданы две прямые y = k1
x + b1
, y = k2
x + b2
, то острый угол между этими прямыми будет определяться как
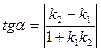 . .
Чтобы две прямые были параллельны необходимо и достаточно, чтобы направляющие векторы этих прямых были коллинеарны, т.е. их соответствующие координаты были пропорциональны.
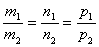
Чтобы две прямые были перпендикулярны необходимо и достаточно, чтобы направляющие векторы этих прямых были перпендикулярны, т.е. косинус угла между ними равен нулю.
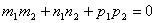
13.
Общее уравнение прямой. Расстояние от точки до прямой.
Уравнение прямой на плоскости.
Определение.
Любая прямая на плоскости может быть задана уравнением первого порядка
Ах + Ву + С = 0,
причем постоянные А, В не равны нулю одновременно, т.е. А2
+ В2
¹ 0. Это уравнение первого порядка называют общим уравнением прямой.
В зависимости от значений постоянных А,В и С возможны следующие частные случаи:
- C = 0, А ¹ 0, В ¹ 0 – прямая проходит через начало координат
- А = 0, В ¹ 0, С ¹ 0 { By + C = 0}- прямая параллельна оси Ох
- В = 0, А ¹ 0, С ¹ 0 { Ax + C = 0} – прямая параллельна оси Оу
- В = С = 0, А ¹ 0 – прямая совпадает с осью Оу
- А = С = 0, В ¹ 0 – прямая совпадает с осью Ох
Теорема. Если задана точка М(х0, у0), то расстояние до прямой Ах + Ву + С =0 определяется как
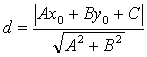
Доказательство. Пусть точка М1(х1, у1) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М1:
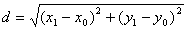 (1) (1)
Координаты x1 и у1 могут быть найдены как решение системы уравнений:
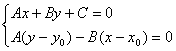
Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М0 перпендикулярно заданной прямой.
Если преобразовать первое уравнение системы к виду:
A(x – x0) + B(y – y0) + Ax0 + By0 + C = 0,
то, решая, получим:
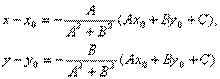
Подставляя эти выражения в уравнение (1), находим:
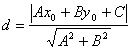 . .
Теорема доказана.
Пример. Определить угол между прямыми: y = -3x + 7; y = 2x + 1.
k1 = -3; k2 = 2 tgj = 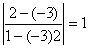 ; j = p/4. ; j = p/4.
Пример. Показать, что прямые 3х – 5у + 7 = 0 и 10х + 6у – 3 = 0 перпендикулярны.
Находим: k1 = 3/5, k2 = -5/3, k1k2 = -1, следовательно, прямые перпендикулярны.
Пример. Даны вершины треугольника А(0; 1), B(6; 5), C(12; -1). Найти уравнение высоты, проведенной из вершины С.
Находим уравнение стороны АВ: 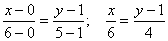 ; 4x = 6y – 6; ; 4x = 6y – 6;
2x – 3y + 3 = 0; 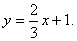
Искомое уравнение высоты имеет вид: Ax + By + C = 0 или y = kx + b.
k = 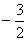 . Тогда y = . Тогда y = 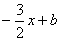 . Т.к. высота проходит через точку С, то ее координаты удовлетворяют данному уравнению: . Т.к. высота проходит через точку С, то ее координаты удовлетворяют данному уравнению: 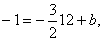 откуда b = 17. Итого: откуда b = 17. Итого: 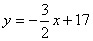 . .
Ответ: 3x + 2y – 34 = 0.
14.
Уравнение прямой, проходящей через данную точку в данном направлении.
Пусть прямая проходит через точку М(xо
;yо
) и ее направление характеризуется угловым коэффициентом k.
Уравнение этой прямой можно записать в виде у
= kx
+ Ь,
где b
—
пока неизвестная величина. Так как прямая проходит через точку М(хо
;уо
),
то координаты точки удовлетворяют уравнению прямой: уо
= kxo
+ Ь.
Отсюда b = уо
— kxo
.
Подставляя значение b
в уравнение у =
kx
+ b,
получим искомое уравнение прямой у
= kx + уо
— kxo
,
т. е.

Уравнение с различными значениями k
называют также уравнениями пучка прямых с
центром в точке М(хо
;уо
).
Из этого пучка нельзя определить лишь прямую, параллельную оси Оу.
15.
Уравнение прямой, проходящей через две данные точки.
Пусть в пространстве заданы две точки M1(x1, y1, z1) и M2(x2, y2, z2), тогда уравнение прямой, проходящей через эти точки:
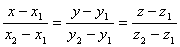
Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.
На плоскости записанное выше уравнение прямой упрощается:
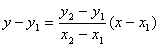
если х1 ¹ х2 и х = х1, еслих1 = х2.
Дробь  = k называется угловым коэффициентом прямой. = k называется угловым коэффициентом прямой.
Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).
Применяя записанную выше формулу, получаем:
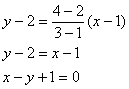
16.
Уравнения плоскости в пространстве.
Плоскостью
называется поверхность, вес точки которой удовлетворяют общему уравнению: Ax + By + Cz + в = 0, где А, В, С – координаты вектора 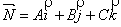 -вектор нормали
к плоскости. Возможны следующие частные случаи: А = 0 – плоскость параллельна оси Ох В = 0 – плоскость параллельна оси Оу С = 0 – плоскость параллельна оси Оz в = 0 – плоскость проходит через начало координат А = В = 0 – плоскость параллельна плоскости хОу А = С = 0 – плоскость параллельна плоскости хОz В = С = 0 – плоскость параллельна плоскости yOz А = в = 0 – плоскость проходит через ось Ох В = в = 0 – плоскость проходит через ось Оу С = в = 0 – плоскость проходит через ось Oz А = В = в = 0 – плоскость совпадает с плоскостью хОу А = С = в = 0 – плоскость совпадает с плоскостью xOz В = С = в = 0 – плоскость совпадает с плоскостью yOz
-вектор нормали
к плоскости. Возможны следующие частные случаи: А = 0 – плоскость параллельна оси Ох В = 0 – плоскость параллельна оси Оу С = 0 – плоскость параллельна оси Оz в = 0 – плоскость проходит через начало координат А = В = 0 – плоскость параллельна плоскости хОу А = С = 0 – плоскость параллельна плоскости хОz В = С = 0 – плоскость параллельна плоскости yOz А = в = 0 – плоскость проходит через ось Ох В = в = 0 – плоскость проходит через ось Оу С = в = 0 – плоскость проходит через ось Oz А = В = в = 0 – плоскость совпадает с плоскостью хОу А = С = в = 0 – плоскость совпадает с плоскостью xOz В = С = в = 0 – плоскость совпадает с плоскостью yOz
Уравнение плоскости, проходящей через три точки.
Для того, чтобы через три какие- либо точки пространства можно было провести единственную плоскость, необходимо, чтобы эти точки не лежали на одной прямой.
Рассмотрим точки М1
(x1
, y1
, z1
), M2
(x2
, y2
, z2
), M3
(x3
, y3
, z3
) в общей декартовой системе координат. Для того, чтобы произвольная точка М(x, y, z) лежала в одной плоскости с точками М1
, М2
, М3
необходимо, чтобы векторы 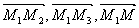 были компланарны. (
были компланарны. (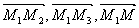 ) = 0 Таким образом,
) = 0 Таким образом, 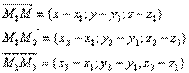 Уравнение плоскости, проходящей через три точки:
Уравнение плоскости, проходящей через три точки: 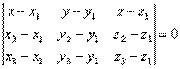
Уравнение плоскости по двум точкам и вектору, коллинеарному плоскости.
Гексаэдр - правильный шестигранник
Вычислим интеграл Математика Задачи Ортогональная система координат в пространстве Математическая модель
Пусть заданы точки М1
(x1
, y1
, z1
), M2
(x2
, y2
, z2
) и вектор 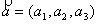 . Составим уравнение плоскости, проходящей через данные точки М1
и М2
и произвольную точку М(х, у, z) параллельно вектору
. Составим уравнение плоскости, проходящей через данные точки М1
и М2
и произвольную точку М(х, у, z) параллельно вектору 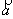 . Векторы
. Векторы 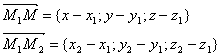 и вектор
и вектор 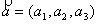 должны быть компланарны, т.е. (
должны быть компланарны, т.е. (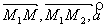 ) = 0 Уравнение плоскости:
) = 0 Уравнение плоскости: 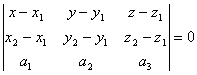
Уравнение плоскости по одной точке и двум векторам,
коллинеарным плоскости.
Пусть заданы два вектора 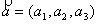 и
и 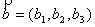 , коллинеарные плоскости. Тогда для произвольной точки М(х, у, z), принадлежащей плоскости, векторы
, коллинеарные плоскости. Тогда для произвольной точки М(х, у, z), принадлежащей плоскости, векторы 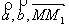 должны быть компланарны.
должны быть компланарны.
Уравнение плоскости: 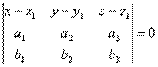
Уравнение плоскости по точке и вектору нормали.
Теорема.
Если в пространстве задана точка М0
(х0
, у0
,
z
0
), то уравнение плоскости, проходящей через точку М0
перпендикулярно вектору нормали
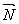 (
A
,
B
,
C
) имеет вид:
A
(
x
–
x
0
) +
B
(
y
–
y
0
) +
C
(
z
–
z
0
) = 0.
(
A
,
B
,
C
) имеет вид:
A
(
x
–
x
0
) +
B
(
y
–
y
0
) +
C
(
z
–
z
0
) = 0.
Доказательство.
Для произвольной точки М(х, у, z), принадлежащей плоскости, составим вектор 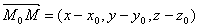 . Т.к. вектор
. Т.к. вектор 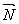 - вектор нормали, то он перпендикулярен плоскости, а, следовательно, перпендикулярен и вектору
- вектор нормали, то он перпендикулярен плоскости, а, следовательно, перпендикулярен и вектору 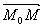 . Тогда скалярное произведение
. Тогда скалярное произведение 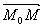 ×
×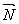 = 0 Таким образом, получаем уравнение плоскости
= 0 Таким образом, получаем уравнение плоскости 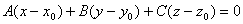 Теорема доказана.
Теорема доказана.
17.
Уравнения прямой в пространстве.
Уравнение прямой в пространстве по точке и
направляющему вектору.
Возьмем произвольную прямую и вектор  (m, n, p), параллельный данной прямой. Вектор (m, n, p), параллельный данной прямой. Вектор 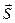 называется направляющим вектором
прямой. называется направляющим вектором
прямой.
На прямой возьмем две произвольные точки М0
(x0
, y0
, z0
) и M(x, y, z).

Обозначим радиус- векторы этих точек как 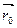 и и  , очевидно, что , очевидно, что  - - 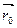 = = 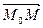 . .
Т.к. векторы 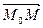 и и 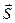 коллинеарны, то верно соотношение коллинеарны, то верно соотношение 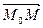 = = 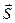 t, где t – некоторый параметр. t, где t – некоторый параметр.
Итого, можно записать:  = = 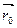 + + 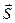 t. t.
Т.к. этому уравнению удовлетворяют координаты любой точки прямой, то полученное уравнение –
параметрическое уравнение прямой
.
Это векторное уравнение может быть представлено в координатной форме:
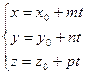
Преобразовав эту систему и приравняв значения параметра t, получаем канонические уравнения прямой в пространстве:
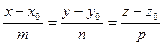 . .
Определение.
Направляющими косинусами
прямой называются направляющие косинусы вектора 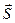 , которые могут быть вычислены по формулам: , которые могут быть вычислены по формулам:
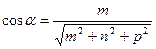 ; ; 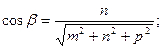 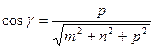 . .
Отсюда получим: m : n : p = cosa : cosb : cosg.
Числа m, n, p называются
угловыми коэффициентами
прямой. Т.к. 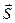 - ненулевой вектор, то m, n и p не могут равняться нулю одновременно, но одно или два из этих чисел могут равняться нулю. В этом случае в уравнении прямой следует приравнять нулю соответствующие числители. - ненулевой вектор, то m, n и p не могут равняться нулю одновременно, но одно или два из этих чисел могут равняться нулю. В этом случае в уравнении прямой следует приравнять нулю соответствующие числители.
Уравнение прямой в пространстве, проходящей
через две точки.
Если на прямой в пространстве отметить две произвольные точки M1
(x1
, y1
, z1
) и M2
(x2
, y2
, z2
), то координаты этих точек должны удовлетворять полученному выше уравнению прямой:
 . .
Кроме того, для точки М1
можно записать:
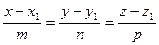 . .
Решая совместно эти уравнения, получим:
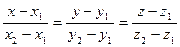 . .
Это уравнение прямой, проходящей через две точки в пространстве.
Общие уравнения прямой в пространстве.
Уравнение прямой может быть рассмотрено как уравнение линии пересечения двух плоскостей.
Как было рассмотрено выше, плоскость в векторной форме может быть задана уравнением:
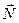 × × + в = 0, где + в = 0, где
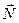 - нормаль плоскости; - нормаль плоскости;  - радиус- вектор произвольной точки плоскости. - радиус- вектор произвольной точки плоскости.
Пусть в пространстве заданы две плоскости: 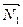 × × + D1
= 0 и + D1
= 0 и 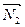 × × + D2
= 0, векторы нормали имеют координаты: + D2
= 0, векторы нормали имеют координаты: 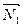 (A1
, B1
, C1
), (A1
, B1
, C1
), 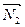 (A2
, B2
, C2
); (A2
, B2
, C2
);  (x, y, z). (x, y, z).
Тогда общие уравнения прямой в векторной форме:
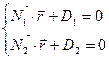
Общие уравнения прямой в координатной форме:
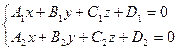
Практическая задача часто состоит в приведении уравнений прямых в общем виде к каноническому виду.
Для этого надо найти произвольную точку прямой и числа m, n, p.
При этом направляющий вектор прямой может быть найден как векторное произведение векторов нормали к заданным плоскостям.
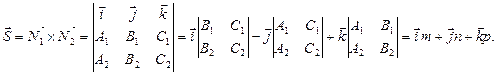
Пример.
Найти каноническое уравнение, если прямая задана в виде:
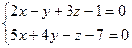
Для нахождения произвольной точки прямой, примем ее координату х = 0, а затем подставим это значение в заданную систему уравнений.
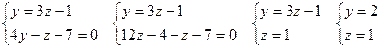 , т.е. А(0, 2, 1). , т.е. А(0, 2, 1).
Находим компоненты направляющего вектора прямой.
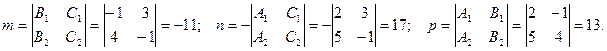
Тогда канонические уравнения прямой:
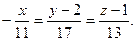
Пример.
Привести к каноническому виду уравнение прямой, заданное в виде:
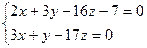
Для нахождения произвольной точки прямой, являющейся линией пересечения указанных выше плоскостей, примем z = 0. Тогда:
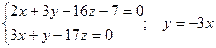 ; ;
2x – 9x – 7 = 0;
x = -1; y = 3;
Получаем: A(-1; 3; 0).
Направляющий вектор прямой: 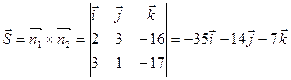 . .
Итого: 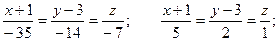
18.
Понятие функции. Способы задания функции.
Одним из основных математических понятий является понятие функции. Понятие функции связано с установлением зависимости (связи) между элементами двух множеств.
Пусть даны два непустых множества X и Y. Соответствие ƒ, которое каждому элементу хÎ X сопоставляет один и только один элемент уÎ Y, называется функцией и записывается у=ƒ(х), хÎ X или ƒ:
X→Y. Говорят еще, что функция ƒ отображает множество X на множество Y.
Числовые функции. График функции. Способы задания функций
Пусть задана функция ƒ : X→Y.
Если элементами множеств X и Y являются действительные числа (т. е. XÌ R и YÌ R), то функцию ƒ называют числовой функцией. В дальнейшем будем изучать (как правило) числовые функции, для краткости будем именовать их просто функциями и записывать у=ƒ(х).
Переменная х называется при этом аргументом или независимой переменной, а у — функцией или зависимой переменной (от х). Относительно самих величин х и у говорят, что они находятся в функциональной зависимости. Иногда функциональную зависимость у от х пишут в виде у=у(х), не вводя новой буквы (ƒ) для обозначения зависимости.
Частное значение
функции ƒ(х) при х=a записывают так: ƒ(a). Например, если ƒ(х)=2х2
-3, то ƒ(0)=-3, ƒ(2)=5.
Графиком функции
у=(х) называется множество всех точек плоскости Оху, для каждой на которых х является значением аргумента, а у — соответствующим значением функции.
Чтобы задать функцию у=ƒ(х), необходимо указать правило, позволяющее, зная х, находить соответствующее значение у.
Наиболее часто встречаются три способа задания функции: аналитический, табличный, графический.
Аналитический способ
:
функция задается в виде одной или нескольких формул или уравнений.
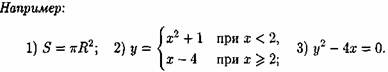
Если область определения функции у = ƒ(х) не указана, то предполагается, что она совпадает с множеством всех значений аргумента, при которых соответствующая формула имеет смысл.Так, областью определения функции у= √(1-х2) является отрезок [-1; 1].
Аналитический способ задания функции является наиболее совершенным, так как к нему приложены методы математического анализа, позволяющие полностью исследовать функцию у=ƒ(х).
Графический способ: задается график функции.
Часто графики вычерчиваются автоматически самопишущими приборами или изображаются на экране дисплея. Значения функции у, соответствующие тем или иным значениям аргумента х, непосредственно находятся из этого графика.
Преимуществом графического задания является его наглядность, недостатком — его неточность.
Табличный способ:
функция задается таблицей ряда значений аргумента и соответствующих значений функции. Например, известные таблицы значений тригонометрических функций, логарифмические таблицы.
На практике часто приходится пользоваться таблицами значений функций, полученных опытным путем или в результате наблюдений.
19.
Основные свойства функций.
1. Четность и нечетность
Функция называется четной, если
– область определения функции симметрична относительно нуля
– для любого х из области определения f(-x) = f(x)
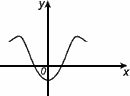
График четной функции симметричен относительно оси 0y
Функция называется нечетной, если
– область определения функции симметрична относительно нуля
– для любого х из области определения f(-x) = –f(x)
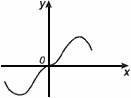
График нечетной функции симметричен относительно начала координат.
2.Периодичность
Функция f(x) называется периодической с периодом 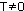 , если для любого х из области определения f(x) = f(x+Т) = f(x-Т)
. , если для любого х из области определения f(x) = f(x+Т) = f(x-Т)
.
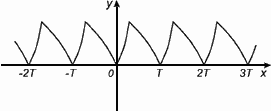
График периодической функции состоит из неограниченно повторяющихся одинаковых фрагментов.
3. Монотонность (возрастание, убывание)
Функция f(x) возрастает на множестве Р , если для любых x1
и x2
из этого множества, таких, что x1
< x2
выполнено неравенство f(x1
)< f(x2
).
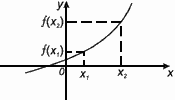
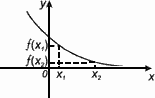
Функция f(x) убывает на множестве Р , если для любых x1
и x2
из этого множества, таких, что x1
< x2
выполнено неравенство f(x1
) > f(x2
).
4. Экстремумы
Точка Хmax
называется точкой максимума функции f(x) , если для всех х из некоторой окрестности Хmax
, выполнено неравенство f(х) f(Xmax
). f(Xmax
).
Значение Ymax
=f(Xmax
) называется максимумом этой функции.
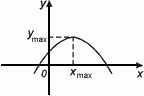
Хmax
– точка максимума
Уmax
– максимум
Точка Хmin
называется точкой минимума функции f(x) , если для всех х из некоторой окрестности Хmin
, выполнено неравенство f(х) f(Xmin
). f(Xmin
).
Значение Ymin
=f(Xmin
) называется минимумом этой функции.
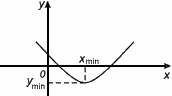
Xmin
– точка минимума
Ymin
– минимум
Xmin
, Хmax
– точки экстремума
Ymin
, Уmax
– экстремумы.
5. Нули функции
Нулем функции y = f(x) называется такое значение аргумента х , при котором функция обращается в нуль: f(x) = 0.
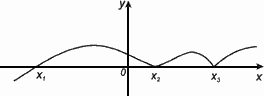
Х1
,Х2
,Х3
– нули функции y = f(x).
20.
Последовательности. Предел числовой последовательности.
Функция f:N® X, областью определения которой является множество натуральных чисел, называется последовательностью.
Если f:N® R, то последовательность называется числовой. Иначе, числовая последовательность – это функция натурального аргумента: xn
= f(n). Обозначают числовую последовательность {xn
}. Примеры числовых последовательностей:
Пример 16.
1) 1,2,..., n,...;
2) 1,-1,1,-1,...,(-1)n
,...;
3) 1,1/2,1/3,...,1/n,....
Последовательность называется ограниченной сверху (снизу), если $ M (m), такое, что для любого nÎ N xn
£ M (xn
³ m).
Последовательность называется ограниченной, если она ограничена и сверху и снизу, то есть $ c > 0 такое, что |xn
| £ c для любого nÎ N. Заметим, что в данном определении c=max{|m|,|M|}.
Пример 17.
1,2,...,n,...
— ограничена снизу, но неограничена сверху;
{1/n
} – ограничена, так как 0< xn
£ 1 ;
{(-1)n
} – ограничена
Последовательность xn
называется неограниченной, если
" c>
0 $ N: |xN
| > c
Неограниченная последовательность может быть односторонне ограниченной, то есть ограниченной или сверху, или снизу. Пример неограниченной сверху последовательности: xn
= n.
Понятие предела числовой последовательности хорошо иллюстрируется на следующем примере. Пусть задана последовательность xn
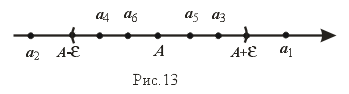
= 1/n. Изобразим ее члены точками на числовой оси (рис. 12).
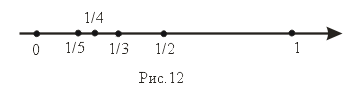
Можно заметить, что члены последовательности с ростом номера n как угодно близко приближаются к 0. При этом величина xn
становится все меньше и меньше. Очевидно, что пределом данной последовательности будет 0.
Дадим строгое определение предела числовой последовательности.
определение предела последовательности.
Число A называется пределом последовательности xn
, если
" U
(A
) $ N:
" n > N xn
Î U
(A
).
Приведем другое определение предела, которое является эквивалентным первому.
определение предела последовательности.
Число A называется пределом xn
, если
" e > 0 $ N:
" n > N |xn
-A |<
e
Заметим, что здесь использованы логические символы: квантор всеобщности " (вместо слова "для любого") и квантор существования $ (вместо слова "найдется").
Предел числовой последовательности обозначается limn
®¥
xn
= A или xn
® A при n® ¥. Последовательность, имеющая предел, называется сходящейся, в противном случае расходящейся.
Пример 18
.
Пусть xn
= 1/n, покажем, что
limn
® ¥
1/n =
0.
Для этого запишем определение:
" e>0 $ N:
" n>N |xn
|<
e.
То есть 1/n<e при n>N=[1/e].
Пример 19.
xn
= 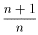 . .
Доказать, что
limn
® ¥
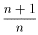 =
1 =
1
" e >0 $ N:
" n > N |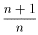 -
1| <
e. -
1| <
e.
1/n <
e Þ n >
1/
e N =
[1/
e]
Если e = 1/10 , то N=10 и при n > 10 следует выполнение нужного неравенства.
Выясним геометрический смысл понятия предела последовательности. Расположим члены последовательности x1
,x2
,..., xn
,... на числовой прямой. Неравенство |xn
-A|<e равносильно следующему A- e < xn
< A + e, которое говорит о том, что члены последовательности xn
попадают в e - окрестность точки A (рис.13). Вне этой e -окрестности может быть лишь конечное число членов данной последовательности.
21.
Предел функции в точке и в бесконечности. Основные теоремы о пределах.
Определение.
Число А называется пределом
функции f(x) при х®¥, если для любого числа e>0 существует такое число М>0, что для всех х, ïхï>M выполняется неравенство
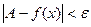
При этом предполагается, что функция f(x) определена в окрестности бесконечности.
Записывают: 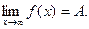
Аналогично можно определить пределы  для любого х>M и для любого х>M и
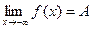 для любого х<M. для любого х<M.
Число А называется пределом функции в точке хо
(или при х→хо
), если для любого положительного ε найдется такое положительное число δ, что для все х¹хо
, удовлетворяющих неравенству |х-хо
|<δ, выполняется неравенство |ƒ(х)-А|<ε.

Предел функции при х
®
∞
Пусть функция у=ƒ(х) определена в промежутке (-∞;∞). Число А называется пределом функции
ƒ(х) при
х→∞
, если для любого положительного числа ε существует такое число М=М()>0, что при всех х, удовлетворяющих неравенству |х|>М выполняется неравенство |ƒ(х)-А|<ε. Коротко это определение можно записать так:


Основные теоремы о пределах.
Теорема 1.
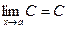 , где С = const. , где С = const.
Следующие теоремы справедливы при предположении, что функции f(x) и g(x) имеют конечные пределы при х®а.
Теорема 2.
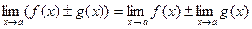
Доказательство этой теоремы будет приведено ниже.
Теорема 3.
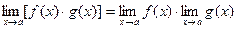
Следствие.
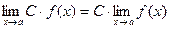
Теорема 4.
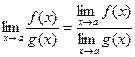 при при 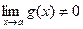
Теорема 5.
Если
f
(
x
)>0 вблизи точки х = а и 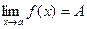 , то А>0. , то А>0.
Аналогично определяется знак предела при f(x) < 0, f(x) ³ 0, f(x) £ 0.
Теорема 6.
Если
g
(
x
)
£
f
(
x
)
£
u
(
x
) вблизи точки х = а и 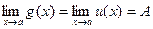 , то и , то и 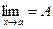 . .
О
пределение.
Функция f(x) называется ограниченной
вблизи точки х = а, если существует такое число М>0, что ïf(x)ï<M вблизи точки х = а.
Теорема 7.
Если функция
f
(
x
) имеет конечный предел при х
®
а, то она ограничена вблизи точки х = а.
Доказательство.
Пусть 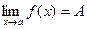 , т.е. , т.е. 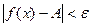 , тогда , тогда
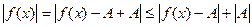 или или
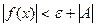 , т.е. , т.е.
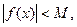 где М = e + ïАï где М = e + ïАï
Теорема доказана.
Пусть функция у=ƒ (х) определена в некоторой окрестности точки хо
, кроме, быть может, самой точки хо
.
Сформулируем два, эквивалентных между собой, определения предела функции в точке.
22.
Бесконечно малые и бесконечно большие величины.
Функция f(x) называется бесконечно малой
при х®а, где а может быть числом или одной из величин ¥, +¥ или -¥, если 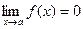 . .
Бесконечно малой функция может быть только если указать к какому числу стремится аргумент х. При различных значениях а функция может быть бесконечно малой или нет.
Пример.
Функция f(x) = xn
является бесконечно малой при х®0 и не является бесконечно малой при х®1, т.к. 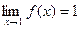 . .
Теорема.
Для того, чтобы функция
f
(
x
) при х
®
а имела предел, равный А, необходимо и достаточно, чтобы вблизи точки х = а выполнялось условие
f
(
x
) =
A
+
a
(
x
),
где
a
(х) – бесконечно малая при х
®
а (
a
(х)
®
0 при х
®
а).
Свойства бесконечно малых функций:
1) Сумма фиксированного числа бесконечно малых функций при х®а тоже бесконечно малая функция при х®а.
2) Произведение фиксированного числа бесконечно малых функций при х®а тоже бесконечно малая функция при х®а.
3) Произведение бесконечно малой функции на функцию, ограниченную вблизи точки х = а является бесконечно малой функцией при х®а.
4) Частное от деления бесконечно малой функции на функцию, предел которой не равен нулю есть величина бесконечно малая.
Используя понятие бесконечно малых функций, приведем доказательство некоторых теорем о пределах, приведенных выше.
Доказательство теоремы 2.
Представим f(x) = A + a(x), g(x) = B + b(x), где
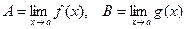 , тогда , тогда
f(x) ± g(x) = (A + B) + a(x) + b(x)
A + B = const, a(х) + b(х) – бесконечно малая, значит
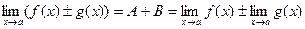
Теорема доказана.
Доказательство теоремы 3.
Представим f(x) = A + a(x), g(x) = B + b(x), где
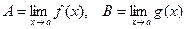 , тогда , тогда
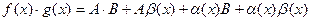
A×B = const, a(х) и b(х) – бесконечно малые, значит
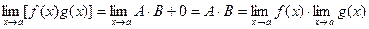
Теорема доказана.
Бесконечно большие функции и их связь с бесконечно малыми.
Определение.
Предел функции f(x) при х®а, где а- число, равен бесконечности
, если для любого числа М>0 существует такое число D>0, что неравенство
ïf(x)ï>M
выполняется при всех х, удовлетворяющих условию
0 < ïx - aï < D
Записывается 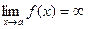 . .
Собственно, если в приведенном выше определении заменить условие ïf(x)ï>M на f(x)>M, то получим:
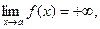
а если заменить на f(x)<M, то:
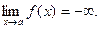
Определение.
Функция называется бесконечно большой
при х®а, где а – чосли или одна из величин ¥, +¥ или -¥, если 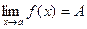 , где А – число или одна из величин ¥, +¥ или -¥. , где А – число или одна из величин ¥, +¥ или -¥.
Связь бесконечно больших и бесконечно малых функций осуществляется в соответствии со следующей теоремой.
Теорема.
Если
f
(
x
)
®
0 при х
®
а (если х
®
¥
) и не обращается в ноль, то
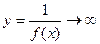
Сравнение бесконечно малых функций.
Пусть a(х), b(х) и g(х) – бесконечно малые функции при х ® а. Будем обозначать эти функции a, b и g соответственно. Эти бесконечно малые функции можно сравнивать по быстроте их убывания, т.е. по быстроте их стремления к нулю.
Например, функция f(x) = x10
стремится к нулю быстрее, чем функция f(x) = x.
Определение.
Если 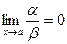 , то функция a называется бесконечно малой более высокого порядка
, чем функция b. , то функция a называется бесконечно малой более высокого порядка
, чем функция b.
Определение.
Если 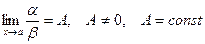 , то a и b называются бесконечно малыми одного порядка
. , то a и b называются бесконечно малыми одного порядка
.
Определение.
Если 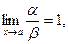 то функции a и b называются эквивалентными бесконечно малыми
. Записывают a ~ b. то функции a и b называются эквивалентными бесконечно малыми
. Записывают a ~ b.
Пример.
Сравним бесконечно малые при х®0 функции f(x) = x10
и f(x) = x.
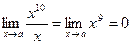
т.е. функция f(x) = x10
– бесконечно малая более высокого порядка, чем f(x) = x.
Определение.
Бесконечно малая функция a называется бесконечно малой порядка
k
относительно бесконечно малой функции b, если предел 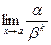 конечен и отличен от нуля. конечен и отличен от нуля.
Однако следует отметить, что не все бесконечно малые функции можно сравнивать между собой. Например, если отношение 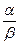 не имеет предела, то функции несравнимы. не имеет предела, то функции несравнимы.
Пример.
Если 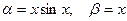 , то при х®0 , то при х®0 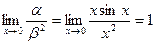 , т.е. функция a - бесконечно малая порядка 2 относительно функции b. , т.е. функция a - бесконечно малая порядка 2 относительно функции b.
Пример.
Если 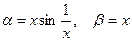 , то при х®0 , то при х®0 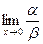 не существует, т.е. функция a и b несравнимы. не существует, т.е. функция a и b несравнимы.
23.
Первый и второй замечательные пределы.
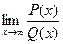 , где P(x) = a0
xn
+ a1
xn-1
+…+an
, , где P(x) = a0
xn
+ a1
xn-1
+…+an
,
Q(x) = b0
xm
+ b1
xm
-1
+…+bm
- многочлены.
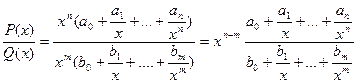
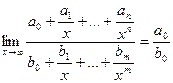
Итого: 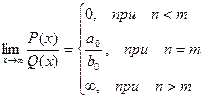
Первый замечательный предел.
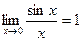
Второй замечательный предел.
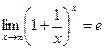
Часто если непосредственное нахождение предела какой – либо функции представляется сложным, то можно путем преобразования функции свести задачу к нахождению замечательных пределов.
Кроме трех, изложенных выше, пределов можно записать следующие полезные на практике соотношения:
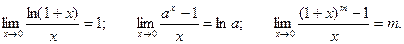
Пример
.
Найти предел.
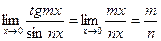
Пример
.
Найти предел.
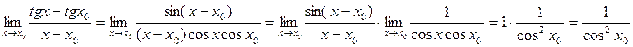
24.
Непрерывность функции. Точки разрыва функции и их классификация.
Определение.
Функция f(x), определенная в окрестности некоторой точки х0
, называется непрерывной в точке
х0
, если предел функции и ее значение в этой точке равны, т.е.
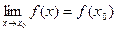
Тот же факт можно записать иначе: 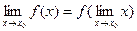
Определение.
Если функция f(x) определена в некоторой окрестности точки х0
, но не является непрерывной в самой точке х0
, то она называется разрывной
функцией, а точка х0
– точкой разрыва.
Определение.
Функция f(x) называется непрерывной в точке х0
, если для любого положительного числа e>0 существует такое число D>0, что для любых х, удовлетворяющих условию
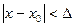
верно неравенство 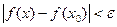 . .
Определение.
Функция f(x) называется непрерывной
в точке х = х0
, если приращение функции в точке х0
является бесконечно малой величиной.
f(x) = f(x0
) + a(x)
где a(х) – бесконечно малая при х®х0
.
Свойства непрерывных функций.
1) Сумма, разность и произведение непрерывных в точке х0
функций – есть функция, непрерывная в точке х0
.
2) Частное двух непрерывных функций 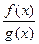 – есть непрерывная функция при условии, что g(x) не равна нулю в точке х0
. – есть непрерывная функция при условии, что g(x) не равна нулю в точке х0
.
3) Суперпозиция непрерывных функций – есть непрерывная функция.
Это свойство может быть записано следующим образом:
Если u = f(x), v = g(x) – непрерывные функции в точке х = х0
, то функция v = g(f(x)) – тоже непрерывнаяфункция в этой точке.
Справедливость приведенных выше свойств можно легко доказать, используя теоремы о пределах.
Точки разрыва и их классификация.
Рассмотрим некоторую функцию f(x), непрерывную в окрестности точки х0
, за исключением может быть самой этой точки. Из определения точки разрыва функции следует, что х = х0
является точкой разрыва, если функция не определена в этой точке, или не является в ней непрерывной.
Следует отметить также, что непрерывность функции может быть односторонней. Поясним это следующим образом.
Если односторонний предел 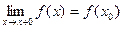 , то функция называется непрерывной справа. , то функция называется непрерывной справа.
Если односторонний предел 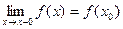 , то функция называется непрерывной слева. , то функция называется непрерывной слева.
Определение.
Точка х0
называется точкой разрыва
функции f(x), если f(x) не определена в точке х0
или не является непрерывной в этой точке.
Определение.
Точка х0
называется точкой разрыва 1- го рода
, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.

Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х0
, достаточно того, что она определена слева и справа от нее.
Из определения можно сделать вывод, что в точке разрыва 1 – го рода функция может иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 – го рода еще иногда называют устранимой
точкой разрыва, но подробнее об этом поговорим ниже.
Определение.
Точка х0
называется точкой разрыва 2 – го рода
, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.
Пример.
Функция f(x) = 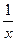 имеет в точке х0
= 0 точку разрыва 2 – го рода, т.к. имеет в точке х0
= 0 точку разрыва 2 – го рода, т.к.
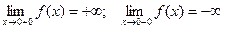 . .
 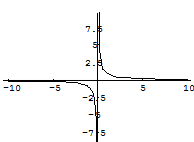
Пример.
f(x) = 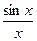
Функция не определена в точке х = 0, но имеет в ней конечный предел 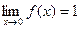 , т.е. в точке х = 0 функция имеет точку разрыва 1 – го рода. Это – устранимая точка разрыва, т.к. если доопределить функцию: , т.е. в точке х = 0 функция имеет точку разрыва 1 – го рода. Это – устранимая точка разрыва, т.к. если доопределить функцию:
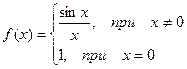
График этой функции:
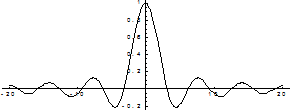
Таким образом, для того, чтобы точка разрыва 1 – го рода была устранимой, необходимо, чтобы односторонние пределы справа и слева были конечны и равны, а функция была бы в этой точке не определена.
25.
Производная функции. Ее геометрический и механический смысл. Основные правила дифференцирования.
Пусть функция у=ƒ(х) определена на некотором интервале (a;b). Проделаем следующие операции:
- аргументу х є (α; b) дадим приращение ∆х: х+∆х є (a; b);
- найдем соответствующее приращение функции: ∆у=ƒ(х+∆х)—ƒ(х);
- составим отношение приращения функции к приращению аргумента: ∆у/∆х;
- найдем предел этого отношения при ∆х→0:
Если этот предел существует, то его называют производной функции ƒ(х) и обозначают одним из символов f'x
, ƒ'(х); у'; у'х;
.dy/dx
Производной функции
у=ƒ(х) β точке х0
называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Итак, по определению

Производная функции ƒ(х) есть некоторая функция f'(x), произведённая из данной функции.
Функция у=ƒ(х), имеющая производную в каждой точке интервала (a;b), называется дифференцируемой в этом интервале; операция нахождения производной функции называется дифференцированием.
Значение производной функции у=ƒ(х) в точке х=х0
обозначается одним из символов: ƒ'(х0
), у'|x=xo
или у'(х0
).
Пример 1
Найти производную функции у=С, С=const.
Решение:
- Значению х даем приращение ∆х;
- находим приращение функции ∆у: ∆у=ƒ(х+∆х)-ƒ(х)=С-С= 0;
- значит, ∆(y)/ ∆(x)=0/∆(x)=0;
- следовательно,

Пример 2
Найти производную функции у=х2
.
Решение:
- Аргументу х даем приращение ∆х;
- находим ∆у: ∆у=(х+∆х)2
—х2
=2х•∆х+(∆х)2
;
- составляем отношение

- находим предел этого отношения:

Таким образом, (х2
)'=2х.
В задаче про скорость прямолинейного движения было получено

Это равенство перепишем в виде V=S't
, т. е. скорость прямолинейного движения материальной точки в момент времени t есть производная от пути S по времени t. В этом заключается механический смысл производной
.
Обобщая, можно сказать, что если функция y=f(x) описывает какой-либо физический процесс, то производная у' есть скорость протекания этого процесса. В этом состоит физический смысл производной.
В задаче про касательную к кривой был найден угловой коэффициент касательной

Это равенство перепишем в виде
ƒ'(х) = tga = k,
т. е. производная ƒ'(х) β точке х равна угловому коэффициенту касательной к графику функции у = ƒ(х) в точке, абсцисса которой равна х. В этом заключается геометрический смысл производной.
Основные правила дифференцирования
Обозначим f(x) = u, g(x) = v- функции, дифференцируемые в точке х.
1) (u v) = u v
2) (uv) = uv + uv
3)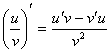 , если v 0 , если v 0
Эти правила могут быть легко доказаны на основе теорем о пределах.
Производные основных элементарных функций:
1)С = 0; 9) 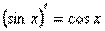
2)(xm
) = mxm
-1
; 10) 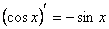
3) 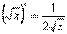 11)
11) 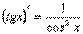
4) 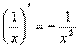 12)
12) 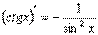
5) 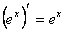 13)
13) 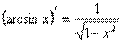
6) 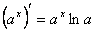 14)
14) 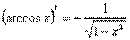
7)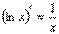 15)
15) 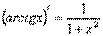
8) 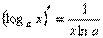 16)
16) 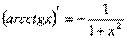
Логарифмическое дифференцирование
Дифференцирование многих функций упрощается, если их предварительно прологарифмировать. Для этого поступают следующим образом. Если требуется найти y' из уравнения y=f(x), то можно:
1. Прологарифмировать обе части уравнения (по основанию е) ln y = ln f(x) = j(x).
2. Продифференцировать обе части равенства, считая ln y сложной функцией от переменной x: 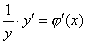 . .
3. Выразить y' = y·j'(x) = f(x)·(lnx)'.
Примеры.
1. y = xa
– степенная функция с произвольным показателем.
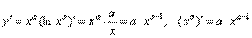 . .
2. 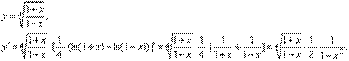
26.
Дифференциал функции. Его геометрический смысл.
Пусть функция y=f(x) дифференцируема на отрезке [a; b]. Производная этой функции в некоторой точке х0
[a; b] определяется равенством
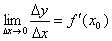
Следовательно, по свойству предела
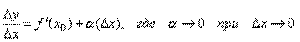
Умножая все члены полученного равенства на Δx, получим:
Δy = f '(x0
)·Δx + a·Δx.
Итак, бесконечно малое приращение Δy дифференцируемой функции y=f(x) может быть представлено в виде суммы двух слагаемых, из которых первое есть (при f '(х0
) ≠ 0) главная часть приращения, линейная относительно Δx, а второе – бесконечно малая величина более высокого порядка, чем Δx. Главную часть приращения функции, т.е. f '(х0
)·Δx называют дифференциалом функции в точке х0
и обозначают через dy.
Таким образом, если функция y=f(x) имеет производную f '(x) в точке x, то произведение производной f '(x) на приращение Δx аргумента называют дифференциалом функции и обозначают:
dy = f '(x)·Δx (1)
Найдем дифференциал функции y= x. В этом случае y' = (x)' = 1 и, следовательно, dy=dx=Δx. Таким образом, дифференциал dxнезависимой переменной xсовпадает с ее приращением Δx. Поэтому формулу (1) мы можем записать так:
dy = f '(x)dx
Но из этого соотношения следует, что 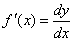 . Следовательно, производную f '(x) можно рассматривать как отношение дифференциала функции к дифференциалу независимой переменной. . Следовательно, производную f '(x) можно рассматривать как отношение дифференциала функции к дифференциалу независимой переменной.
Ранее мы показали, что из дифференцируемости функции в точке следует существование дифференциала в этой точке.
Справедливо и обратное утверждение.
Если для данного значения x приращение функции Δy = f(x+Δx) – f(x) можно представить в виде Δy = A·Δx + α, где α – бесконечно малая величина, удовлетворяющая условию 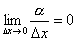 , т.е. если для функции y=f(x) существует дифференциал dy=A·dx в некоторой точке x, то эта функция имеет производную в точке x и f '(x)=А. , т.е. если для функции y=f(x) существует дифференциал dy=A·dx в некоторой точке x, то эта функция имеет производную в точке x и f '(x)=А.
Действительно, имеем 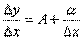 , и так как , и так как 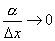 при Δx→0, то при Δx→0, то 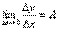 . .
Таким образом, между дифференцируемостью функции и существованием дифференциала имеется очень тесная связь, оба понятия равносильны.
Примеры.
Найти дифференциалы функций:
1. 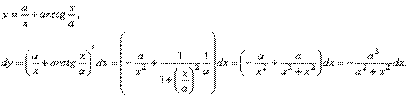
2.  . .
Геометрический смысл дифференциала
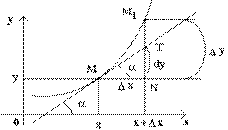
Рассмотрим функцию y=f(x) и соответствующую ей кривую. Возьмем на кривой произвольную точку M(x; y), проведем касательную к кривой в этой точке и обозначим через α угол, который касательная образует с положительным направлением оси Ox. Дадим независимой переменной x приращение Δx, тогда функция получит приращение Δy = NM1
. Значениям x+Δx и y+Δy на кривой y = f(x) будет соответствовать точка
M1
(x+Δx; y+Δy).
Из ΔMNT находим NT=MN·tg α. Т.к. tg α = f '(x), а MN = Δx, то NT = f '(x)·Δx. Но по определению дифференциала dy=f '(x)·Δx, поэтому dy = NT.
Таким образом, дифференциал функции f(x), соответствующей данным значениям x и Δx, равен приращению ординаты касательной к кривой y=f(x) в данной точке х.
27.
Основные теоремы дифференциального исчисления. Раскрытие неопределенностей по правилу Лопиталя.
Основные теоремы о дифференциалах легко получить, используя связь дифференциала и производной функции (dy=f'(x)dx) и соответствующие теоремы о производных.
Например, так как производная функции у=с равна нулю, то дифференциал постоянной величины равен нулю: dy=с'dx=0•dx=0.
Теорема.1.
Дифференциал суммы, произведения и частного двух дифференцируемых функций определяются следующими формулами:

Докажем, например, вторую формулу. По определению дифференциала имеем:
d(uv)=(uv)'dx=(uv'+vu')dx=vu'dx+uv'dx=udv+vdu
Теорема 2.
Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента.
Пусть у=ƒ(u) и u=φ(х) две дифференцируемые функции, образующие сложную функцию у=ƒ(φ(х)). По теореме о производной сложной функции можно написать
у'х
=у'u
•u'x
.
Умножив обе части этого равенства на dx, поучаем у'х
dx=у'u
•u'х
dx. Но у'х
dx=dy и u'х
dx=du. Следовательно, последнее равенство можно переписать так:
dy=у'u
du.
Сравнивая формулы dy=у'х
•dx и dy=у'u
•du, видим, что первый дифференциал функции у=ƒ(х) определяется одной и той же формулой независимо от того, является ли ее аргумент независимой переменной или является функцией другого аргумента.
Это свойство дифференциала называют инвариантностью (неизменностью) формы первого дифференциала.
Формула dy=у'х
•dx по внешнему виду совпадает с формулой dy=у'u
•du, но между ними есть принципиальное отличие: в первой формуле х — независимая переменная, следовательно, dx=∆х, во второй формуле и есть функция от х, поэтому, вообще говоря, du≠∆u.
С помощью определения дифференциала и основных теорем о дифференциалах легко преобразовать таблицу производных в таблицу дифференциалов.
Например: d(cosu)=(cosu)'u
du=-sinu•
du
Таблица дифференциалов
  
Теорема (правило Лопиталя
). Пусть функции f(x)
и g(x)
дифференцируемы в некоторой окрестности точки a
, за исключением, быть может, самой точки a
, и пусть 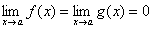 или или 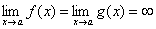 . Тогда, если существует предел отношения производных этих функций . Тогда, если существует предел отношения производных этих функций 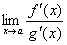 , то существует и предел отношения самих функций f(x)/g(x)
при x
→а,
причем , то существует и предел отношения самих функций f(x)/g(x)
при x
→а,
причем
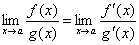 (1) (1)
Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.
Замечание
. Отметим, что формула (1) справедлива только в том случае, если предел, стоящий справа, существует. Может случиться, что предел, стоящий слева существует, в то время как предел, стоящий в правой части равенства, не существует.
Например, найти 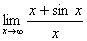 . Этот предел существует . Этот предел существует  . Но отношение производных (
1+
cosx)/
1=
1+
cos x
при x
→∞ не стремится ни к какому пределу. . Но отношение производных (
1+
cosx)/
1=
1+
cos x
при x
→∞ не стремится ни к какому пределу.
Заметим, что если отношение производных опять представляет собой неопределенность вида 0/0 или ∞/∞, то можно снова применить сформулированную теорему, то есть перейти к отношению вторых производных и так далее.
Вспомним, что к этим двум случаям сводятся случаи других неопределенностей: ∞·∞; 0·∞.
Для раскрытия неопределенностей 1∞
, 10
, ∞0
нужно прологарифмировать данную функцию и найти предел ее логарифма.
Примеры.
1. 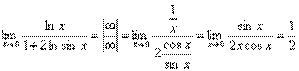 . .
2. 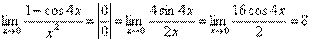 . .
3. 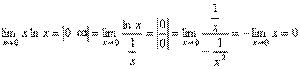 . .
28.
Частные и полные приращения функции. Частные производные функции двух переменных.
Частным приращением функции z = (х, у) по х называется разность (х, у) по х называется разность частным приращением по частным приращением по
О: Частной производной по х от функции z = (x, у) называется предел отношения частного приращения (x, у) называется предел отношения частного приращения к приращению Ах при стремлении последнего к нулю: к приращению Ах при стремлении последнего к нулю:
Другие обозначения: Аналогично и для перемен- Аналогично и для перемен-
ной у.
Заметив, что определяется при неизменном у, а определяется при неизменном у, а — при неизменном х, можно сформулировать правило: частная производная по х от функции z = — при неизменном х, можно сформулировать правило: частная производная по х от функции z = (х, у) есть обычная производная по х, вычисленная в предположении, что у = const. Аналогично для вычисления частной производной по у надо считать х = const. Таким образом, правила вычисления частных производных те же, что и в случае функции одной переменной. (х, у) есть обычная производная по х, вычисленная в предположении, что у = const. Аналогично для вычисления частной производной по у надо считать х = const. Таким образом, правила вычисления частных производных те же, что и в случае функции одной переменной.
Примеры:
1)
2)
Частные производные функции нескольких переменных  определяются аналогично: определяются аналогично:

Из геометрического смысла производной функции одной переменной имеем где где — угол наклона касательной к — угол наклона касательной к в т. М(х, у, z) к оси ОХ. Аналогично для в т. М(х, у, z) к оси ОХ. Аналогично для
Пример: Найти угловые коэффициенты касательных к  поверхности поверхности в т. А(2, 3). в т. А(2, 3).

олным приращением функции z = (х, у) называется разность (х, у) называется разность
Замечание. В общем случае Пусть, например, Пусть, например,

Аналогично полное приращение функции

О: Функция z = (х, у) называется дифференцируемой в т. М(х, у), если ее полное приращение (х, у) называется дифференцируемой в т. М(х, у), если ее полное приращение представимо в виде представимо в виде где А, В не зависят от где А, В не зависят от
 а функция а функция является бесконечно малой более высокого порядка малости по сравнению с является бесконечно малой более высокого порядка малости по сравнению с
 при при 0. Полным дифференциалом дифференцируемой функции в т. М(х, у) называется 0. Полным дифференциалом дифференцируемой функции в т. М(х, у) называется

Докажем необходимое условие дифференцируемости функции. Т: Если функция z = (х, у) дифференцируема в т. М(х, у), то в этой точке существуют частные производные по х и y. (х, у) дифференцируема в т. М(х, у), то в этой точке существуют частные производные по х и y.
причем
Выразим A и В через z = (х, у). Пусть (х, у). Пусть = 0, тогда = 0, тогда  т.е. т.е.


Аналогично

Поэтому

где обозначены
Можно показать, что обратное утверждение в общем случае неверно. Однако имеет место следующая теорема (достаточные условия дифференцируемости функции):
Т: Если частные производные непрерывны в т. М(х,у), непрерывны в т. М(х,у),
то функция z = (х, у) дифференцируема в этой точке Аналогично для функции (х, у) дифференцируема в этой точке Аналогично для функции вводится понятие дифференцируемости и полного дифференциала вводится понятие дифференцируемости и полного дифференциала

Пример: Найти и и для функции z - ху в т. М(2, 3) при для функции z - ху в т. М(2, 3) при  = 0,1; = 0,1; =0,2. =0,2.

= 3 · 0,1 +2·0,2 + 0,1 · 0,2 = 0,72;
 = 3 · 0,1 + 2 · 0,2 = 0,7 = 3 · 0,1 + 2 · 0,2 = 0,7
Пусть функция z = (х, у) дифференцируема в т.(х, у). Найдем (х, у) дифференцируема в т.(х, у). Найдем
 откуда и откуда и Поскольку можно считать при малых Поскольку можно считать при малых что что то верно то верно
 (11.1) (11.1)
с точностью до б.м. высшего порядка малости относительно Ах и  Формулой (11.1) можно пользоваться для приближенных вычислений значений функции двух переменных в т. Формулой (11.1) можно пользоваться для приближенных вычислений значений функции двух переменных в т.
 близкой к т. М(х, у), если известны значения функции и ее частных производных в самой т. М. близкой к т. М(х, у), если известны значения функции и ее частных производных в самой т. М.
Пример: Скорость истечения газа, находящегося под высоким давлением в сосуде, через отверстие в стенке вычисляют по формуле в сосуде, через отверстие в стенке вычисляют по формуле

где k, R — величины, зависящие от химического состава газа,  — температура и давление в сосуде, — температура и давление в сосуде, — давление в окружающей среде. Пусть значения к = 1,5, R = 294, — давление в окружающей среде. Пусть значения к = 1,5, R = 294, = 0,1, = 0,1,  = 100, = 100, =617 =617 =500. =500.
Найти скорость истечения газа при изменениях до 108, до 108,  до 600, R до 300. до 600, R до 300.

Находим производные. Они равны соответственно:

 Тогда Тогда =500 + 0,0817 · 8 + 0,397 · (-17) + + 0,0833 · 6 = 498,89. Непосредственное вычисление дает =500 + 0,0817 · 8 + 0,397 · (-17) + + 0,0833 · 6 = 498,89. Непосредственное вычисление дает  = 494 = 494
29.
Экстремум функции двух переменных.
Определение.
Если для функции z = f(x, y), определенной в некоторой области, в некоторой окрестности точки М0
(х0
, у0
) верно неравенство
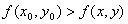
то точка М0
называется точкой максимума.
Определение.
Если для функции z = f(x, y), определенной в некоторой области, в некоторой окрестности точки М0
(х0
, у0
) верно неравенство
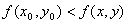
то точка М0
называется точкой минимума.
Теорема. (Необходимые условия экстремума).
Если функция f(x,y) в точке (х0
, у0
) имеет экстремум, то в этой точке либо обе ее частные производные первого порядка равны нулю 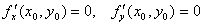 , либо хотя бы одна из них не существует.
, либо хотя бы одна из них не существует.
Эту точку (х0
, у0
) будем называть критической точкой.
Теорема. (Достаточные условия экстремума).
Пусть в окрестности критической точки (х0
, у0
) функция f(x, y) имеет непрерывные частные производные до второго порядка включительно. Рассмотрим выражение:
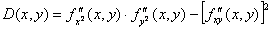
1) Если D(x0
, y0
) > 0, то в точке (х0
, у0
) функция f(x, y) имеет экстремум, если
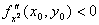 - максимум, если
- максимум, если 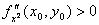 - минимум.
- минимум.
2) Если D(x0
, y0
) < 0, то в точке (х0
, у0
) функция f(x, y) не имеет экстремума
В случае, если в = 0, вывод о наличии экстремума сделать нельзя.
Условный экстремум.
Условный экстремум
находится, когда переменные х и у, входящие в функцию u = f( x, y), не являются независимыми, т.е. существует некоторое соотношение
j(х, у) = 0, которое называется уравнением связи.
Тогда из переменных х и у только одна будет независимой, т.к. другая может быть выражена через нее из уравнения связи.
Тогда u = f(x, y(x)).
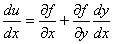
В точках экстремума:
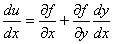 =0 (1)
=0 (1)
Кроме того:
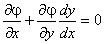 (2)
(2)
Умножим равенство (2) на число l и сложим с равенством (1).
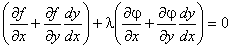
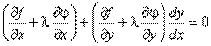
Для выполнения этого условия во всех точках найдем неопределенный коэффициент l так, чтобы выполнялась система трех уравнений:
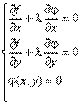
Полученная система уравнений является необходимыми условиями условного экстремума. Однако это условие не является достаточным. Поэтому при нахождении критических точек требуется их дополнительное исследование на экстремум.
Выражение u = f(x, y) + lj(x, y) называется функцией Лагранжа.
Пример.
Найти экстремум функции f(x, y) = xy, если уравнение связи:
2x + 3y – 5 = 0
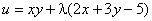
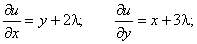
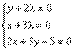
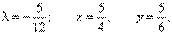
Таким образом, функция имеет экстремум в точке 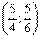 .
.
Использование функции Лагранжа для нахождения точек экстремума функции называется также методом множителей Лагранжа.
30.
Понятие неопределенного интеграла. Свойства неопределенного интеграла.
В дифференциальном исчислении решается задача: по
д
анной функции ƒ(х) найти ее производную
(или дифференциал). Интегральное исчисление решает обратную задачу: найти функцию F(x), зная ее производную F'
(x)=ƒ(х) (или дифференциал). Искомую функцию F(x) называют первообразной функции ƒ(х) .
Функция F(x) называется первообразной
функции ƒ(х) на интервале (а; b), если для любого х є (а;b) выполняется равенство
F'
(x)=ƒ(x) (или dF(x)=ƒ(x)dx).
Например
, первообразной функции у=х2
, х є R, является функция 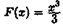 , так как , так как
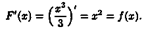
Очевидно, что первообразными Будут также любые функции
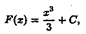
где С - постоянная, поскольку
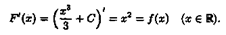
Tеоpeмa 29. 1. Если функция F(x) является первообразной функции ƒ(х) на (а;b), то множество всех первообразных для ƒ(х) задается формулой F(x)+С, где С - постоянное число.
▲Функция F(x)+С является первообразной ƒ(х).
Действительно, (F(x)+C)'
=F'
(x)=ƒ(x).
Пусть Ф(х) - некоторая другая, отличная от F(x), первообразная функции ƒ(х) , т. е. Ф'
(x)=ƒ(х). Тогда для любого х є (а;b) имеем
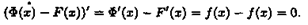
А это означает, что
Ф(x)-F(x)=C,
где С - постоянное число. Следовательно, Ф(х)=F(x)+С.
Множество всех пepвoобpaзныx функций F(x)+С для ƒ(х) называется неопределенным интегралом от функции ƒ(х)
и обозначается символом ∫ ƒ(х) dx.
 Таким образом, по определению Таким образом, по определению
∫ƒ(x)dx= F(x)+C.
Здесь ƒ(х) называется подынтегральнoй функцией
, ƒ(x)dx — подынтегральным выражением,
х - переменной интегрирования
, ∫ - знаком неопределенного интеграла
.
Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.
Геометрически неопределенный интеграл представляет собой семейство «параллельных» кривых у=F(x)+C (каждому числовому значению С соответствует определенная кривая семейства) (см. рис. 166). График каждой первообразной (кривой) называется интегральной кривой
.
Для всякой ли функции существует неопределенный интеграл?
Имеет место теорема, утверждающая, что «всякая непрерывная на (а;b) функция имеет на этом промежутке первообразную», а следoвaтельно, и неопределенный интеграл.
· Свойства неопределенного интеграла
Отметим ряд свойств неопределенного интеграла, вытекающих из его определения.
1. Дифференциал от неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции:
d(
∫ƒ(x)dx)=ƒ(x)dх, (
∫ƒ(x)dx)'
=ƒ(х).
Дeйcтвительнo, d(∫ƒ(х) dx)=d(F(x)+С)=dF(x)+d(C)=F'
(x) dx =ƒ(х) dx
(
∫ƒ (x) dx)'
=(F(x)+C)'=F'(x)+0 =ƒ (x).
Блaгoдapя этому свойству правильность интегрирования проверяется дифференцированием. Например, равенство
∫(3x2
+ 4) dx=хз
+4х+С
верно, так как (х3
+4х+С)'=3x2
+4.
2. Hеопpедeлeнный интеграл от диффepeнциaла некоторой функции равен сумме этой функции и произвольной постоянной:
∫dF(x)= F(x)+C.
Действительно,

3. Постоянный множитель можно выносить за знак интеграла:
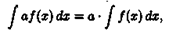 α ≠ 0 - постоянная. α ≠ 0 - постоянная.
Действительно,
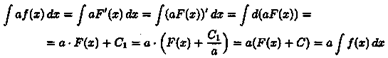
(положили С1
/а=С. )
4. Неопределенный интеграл от aлгeбpaическoй суммы конечного числа непрерывных функций равен aлгебpaичecкoй сумме интегралов от слагаемых функций:
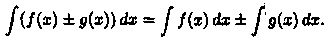
Пусть F'(x)=ƒ(х) и G'(x)=g(x). Тогда
где С1
±С2
=С.
5. (Инвариантность формулы интегрирования).
Если  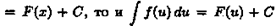 , где u=φ(х) - произвольная функция, имеющая непрерывную производную. , где u=φ(х) - произвольная функция, имеющая непрерывную производную.
Пусть х - независимая переменная, ƒ(х) - непрерывная функция и F(x) - ее пepвoобpaзнaя. Тогда
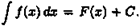
Положим теперь u=ф(х), где ф(х) - непрерывно-дифференцируемая функция. Рассмотрим сложную функцию F(u)=F(φ(x)). В силу инвараинтности формы первого дифференциала функции (см. с. 160) имеем
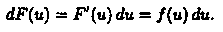
Отсюда 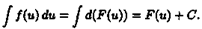
Таким образом, формула для неопределенного интеграла остается справедливой независимо от того, является ли переменная интегрирования независимой переменной или любой функцией от нее, имеющей непрерывную производную.
Так, из формулы 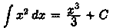 путем замены х на u (u=φ(х)) получаем путем замены х на u (u=φ(х)) получаем 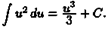
В частности,
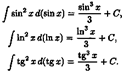
31.
Метод замены переменной в неопределенном интеграле. Интегрирование по частям в неопределенном интеграле.
· Метод интегрирования подстановкой (заменой переменной)
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (т. е. подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводащимся (в случае «удачной» подстановки). Общих методов подбора подстановок не существует. Умение правильно oпpeделить подстановку пpиобpетaeтcя практикой.
Пусть тpебyетcя вычислить интеграл 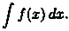 Сделаем подстановку Сделаем подстановку
х =φ(t), где φ(t) - функция, имеющая непрерывную производную.
Тогда dx=φ'
(t) dt и на основании свойства инвариантности формулы интегрирования неопpeделeннoгo интеграла получаем формулу интегриpoвaния подcтaнoвкoй
 1. 1.
Формула (1) также называется формулой замены переменных в неопределeннoм интеграле. Пoслe нахождения интеграла правой части этого равенства следует перейти от новой переменной интегрирования t назад к переменной х.
Иногда целесообразно подбирать подстановку в виде t= φ(х), тогда
Другими слoвaми, формулу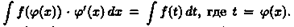 (1) можно применять справа налево. (1) можно применять справа налево.
Пример
Найти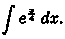
Решение: Положим х=4t, тогда dx=4 dt. Cлeдoвaтельнo,

Пpимep 2.
Найти 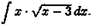
Решение: Пусть 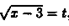 , тогда х=t2
+3, dx=2t dt. Поэтому , тогда х=t2
+3, dx=2t dt. Поэтому
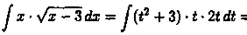 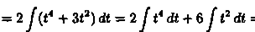 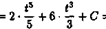 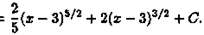
· Метод интегрирования по частям
Пусть u=u(х) и ν=v(х) - функции, имеющие непрерывные производные. Тогда d(uv)=u•dv+v•du.
Интегрируя это равенство, получим

Полученная формула называется формулой интегрирования по частям
. Она дает возможность свести вычисление интеграла 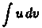 к вычислению интеграла к вычислению интеграла 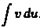 , который может оказаться существенно более простым, чем исходный. , который может оказаться существенно более простым, чем исходный.
Интегрирование по частям состоит в том, что подынтегральное выражение заданного интеграла представляется каким-либо обpaзoм в виде произведения двух сомножителей и и dv (это, как правило, можно осуществить несколькими cспособами); затем, после нахождения ν и du, используется формула интегрирования по частям. Иногда эту формулу приходится использовать несколько раз.
Укажем некоторые типы интегралов, которые удюбно вычислять методом интегрирования по частям.
1. Интегралы вида 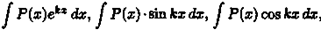 где где
Р(х) - многочлен, К - число. Удобно положить u=Р(х), а за dv обoзнaчить все остальные сомножители.
2.Интегралы вида 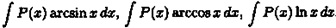 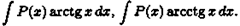 Удобно положить Р(х)dx=dv, а за u обозначить остальные сомножители. Удобно положить Р(х)dx=dv, а за u обозначить остальные сомножители.
3. Интегралы вида 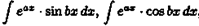 , где а и b - числа. , где а и b - числа.
За и можно принять функциюu=еαх
.
Пример
Найти 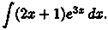
Решение: Пусть(можно положить С=0). Следовательно,
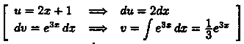
по формуле интегрирования по частям:
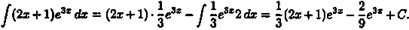
32.
Интегрирование рациональных дробей.
Дробно-рациональной функцией
(или рациональной дробью
) называется функция, равная отношению двух многочленов, т. е. ƒ(х) = 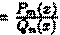 , где Рm
(х) - многочлен степени т, а Qn
(x) - многочлен степени n. , где Рm
(х) - многочлен степени т, а Qn
(x) - многочлен степени n.
Рациональная дpобь называется правильной если степень числителя меньше степени знаменателя, т. е. m<n; в противном случае (если т ип ) рациональная дробь называется неправильной.
Найдем интегралы от проcтeйшиx рациональных дробей.
1. 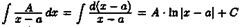 таблица интегралов таблица интегралов
2.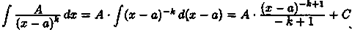 ; таблица интегралов ; таблица интегралов
3. Рассмотрим интеграл 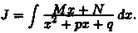
Выделив в знаменателе полный квадрат, получим:
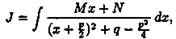
причем  . Сделаем подстановку . Сделаем подстановку 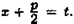 Тогда Тогда 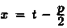 , dx=dt. Положим , dx=dt. Положим 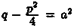 . Следовательно, используя формулы таблицы интегралов, получаем . Следовательно, используя формулы таблицы интегралов, получаем
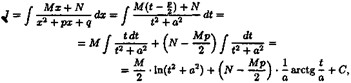
т. е., возвращаясь к переменной х,
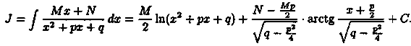
Пример
Найти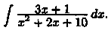
Решение: х2
+2х+10=(х+1)2
+9. Сделаем подстановку х+1=t. Тогда х=t-1, dx=dt и
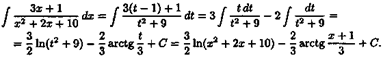
4. Вычисление интеграла вида 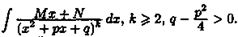
Данный интеграл подстановкой сводится к сумме двух интегралов: 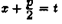
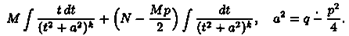
Первый интеграл легко вычисляется:
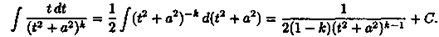
Вычислимвторой интеграл:
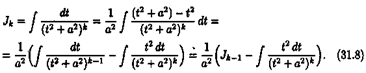 1 1
К последнему интегралу применим интегрирование по частям. Положим
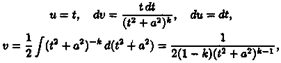
тогда
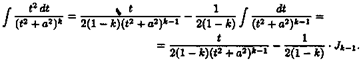
Подставляя найденный интеграл в равенство (1), получаем
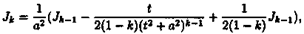
т. е. 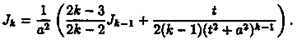
Полученная формула дает возможность найти интеграл Jк
для любого натурального числа k>1.
Интегрирование рациональных дробей
Рассмотренный материал позволяет сформулировать общее правило интегрирования рациональных дробей.
1. Если дpобь неправильна, то представить ее в виде суммы многочлена и правильной дpоби (см. пункт 2);
2. Разложив знаменатель правильной рациональной дpоби на множители, представить ее в виде суммы простейших рациональных дробей;
3. Проинтегрировать многочлен и полученную сумму простейших дробей.
Пример 31. 7.
Найти интеграл 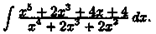
Решение: Под знаком интеграла неправильная дробь; выделим ее целую часть путем деления числителя на знаменатель:
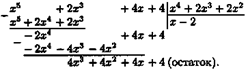
Пoлyчаем:
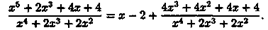
Разложим правильную рациональную дробь на простейшие дроби:
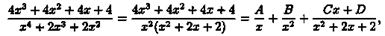
4х3
+4х2
+4х+4 ≡ Ах(х2
+2х+2)+В(х2
+2х+2)+(Сх+D)x2
, т. е.
4х3
+4х2
+4х+4 ≡ (А+С)х3
+(2А+В+D)x2
+(2А+2В)х+2В.
Отсюда следует, что
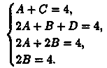
Находим: В=2, А=О, С=4, D=2. Стало быть,
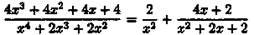
и
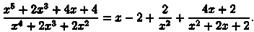
Интегрируем полученное равенство:
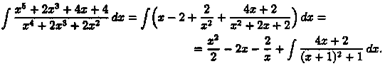
Обозначим х+1=t, тогда х=t-1 и dx=dt. Таким обpaзoм,
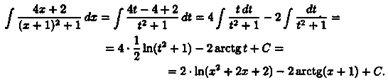
Следовательно,

Отметим, что любая рациональная функция интегрируется в элементарных функциях.
33.
Интегрирование тригонометрических функций с помощью универсальной тригонометрической подстановки.
Рассмотрим некоторые случаи нахождения интеграла от тригонометрических функций. Функцию с переменными sin x и cos x, над которыми выполняются рациональные действия (сложения, вычитание, умножение и деление) принято обозначать R(sin x;cos x), где R - знак рациональной функции.
Вычисление неопределенных интегралов типа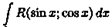 сводится к вычислению интегралов от paциoнaльнoй фyнкции подстановкой сводится к вычислению интегралов от paциoнaльнoй фyнкции подстановкой 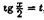 , которая называется универсальной. , которая называется универсальной.
Действительно,
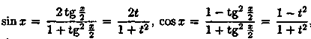 , ,
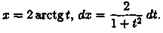
Поэтому
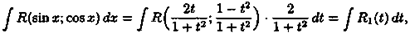
где R1
(t) - рациональная функция от t. Обычно этот способ весьма громоздкий, зато он всегда приводит к результату.
На практике применяют и другие, более простые подстановки, в зависимости от свойств (и вида) подынтегральной фyнкции. В частнocти, удобны следующие правила:
1) если функция R(sinx;cos x) нечетна относительно
sinx, т.е. R(— sinx;cos x)=— R(sin x;cos x), то подстановка cosx=t рационализирует интеграл;
2) если функция R(sinx;cos x) нечетна относительно
cosx, т.е. R(sinx; - cosx)=—R(sinx;cosx), то делается подстановка sinx=t;
3) если функция R(sin x; cos x) четна относительно
sinx и cosx R(— sin x; - cos x)=R(sin x; cos x), то интеграл рационализируется подстановкой tgx=t. Такая же подстановка применяется, если интеграл имеет вид 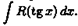
Пример
Найти интеграл 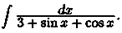
Решение: Cделаем универсальную подстановку 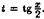 Тогда dx= Тогда dx= 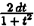 , , 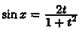 , , 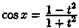 . Следовательно, . Следовательно,
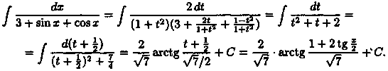
34.
Некоторые особые тригонометрические подстановки.
Интегралы типа ∫sinmх•cosnx dx
Для нахождения таких интегралов используются следующие приемы:
1) подстановка sinx=t, если n - целое положительное нечетное число;
2) подстановка cosx=t, если m - целое положительное нечетное число;
3) формулы понижения порядка: cos2
x=1/2(1+cos2x), sin2
x =1/2(1-cos 2x), sinx-cosx =1/2 sin2x, если тип - целые неотрицательные четные числа;
4) подстановка tg х=t, если m+n - есть четное отрицательное целое число.
Пример
Найти интеграл 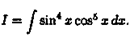
Решение: Применим подстановку sinx=t. Тогда х=arcsint, dx 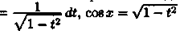 И И
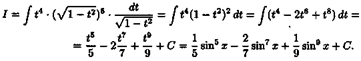
Использование тригонометрических преобразований
Интегралы типа 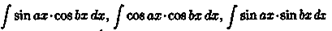 вычисляются с помощью известных формул тригонометрии: вычисляются с помощью известных формул тригонометрии:
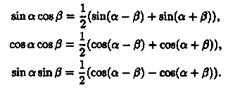
Пример
Найти интеграл 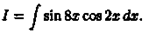
Решение:
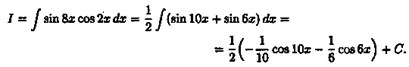
35.
Интегрирование иррациональных выражений.
Квадратичные иррациональности
Рассмотрим некоторые типы интегралов, содержащих иррациональные функции.
Интегралы типа 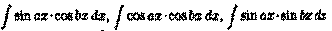 называют неопределенными интегралами от квадратичных иррациональностей. Их можно найти следующим обpaзoм: называют неопределенными интегралами от квадратичных иррациональностей. Их можно найти следующим обpaзoм:
под радикалом выделить полный квадрат
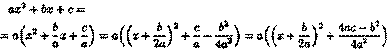
и сделать подстановку х +b/2a=t. При этом первые два интеграла приводятся к табличным, а третий - к сумме двух табличных интегралов.
Пример
Найти интегралы 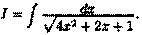
Решение: Так как, 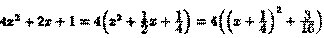
то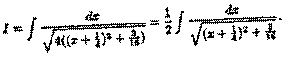
Cдeлаем подстановку x+1/4=t, x=t-1/4,dx=dt. Тогда
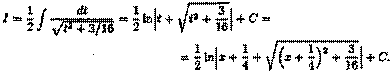
Интегралы типа
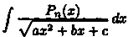 , где Рn
(х) - многочлен степени n, можно вычислять, пользуясь формулой , где Рn
(х) - многочлен степени n, можно вычислять, пользуясь формулой
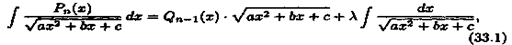 1. 1.
где Qn-1
(x) - многочлен степени n-1 с неопpедeлeнными коэффициентами, l - также неопределенный коэффициент.
Все неопределенные коэффициенты находятся из тождества, получаемого дифференцированием обеих частей равенства (1):
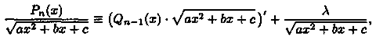
после чего необходимо приравнять коэффициенты при одинаковых степенях неизвестной х.
Пример
Найти интеграл 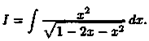
Решение: По формуле (1) имеем:
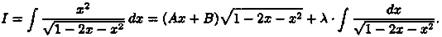
Дифференцируя это равенство, получаем:

Сравниваем коэффициенты при одинаковых степенях х:
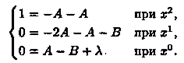
Отсюда А=-1/2,B=3/2,l=2. Следовательно,
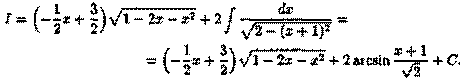
Дробно-линейная подстановка
Интегралы типа 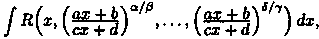 где а, b, с, в - действительные числа, a,b,...,d,g - натуральные числа, сводятся к интегралам от рациональной функции путем подстановки где а, b, с, в - действительные числа, a,b,...,d,g - натуральные числа, сводятся к интегралам от рациональной функции путем подстановки 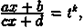 где К - наименьшее общee кратное знаменателей дробей где К - наименьшее общee кратное знаменателей дробей 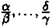
Действительно, из подстановки 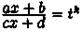 следует, что следует, что 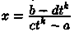 и и
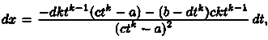
т. е. х и dx выражаются через рациональные функции от t. При этом и каждая степень дроби 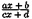 выражается через рациональную функцию от t. выражается через рациональную функцию от t.
Пример
Найти интеграл 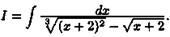
Решение: Наименьшее общee кратное знаменателей дробей 2/3 и 1/2 есть 6.
Поэтому полагаем х+2=t6
, х=t6
-2, dx=6t5
dt, 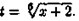 Следовательно, Следовательно,
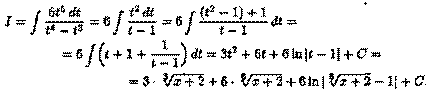
Пример
Указать подстановку для нахождения интегралов:
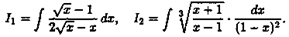
Решение: Для I1
подстановка х=t2
, для I2
подстановка 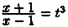
Тригонометрическая подстановка
Интегралы типа приводятся к интегралам 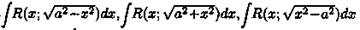 от функций, рационально зависящих от тригонометрических функций, с помощью следующих тригонометрических подстановок: х=а•sint для первого интеграла; х=а•tgt для второго интеграла; от функций, рационально зависящих от тригонометрических функций, с помощью следующих тригонометрических подстановок: х=а•sint для первого интеграла; х=а•tgt для второго интеграла; 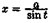 для третьего интеграла. для третьего интеграла.
Интегралы типа
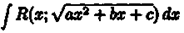
Здесь подынтегральная функция есть рациональная функция относительно х и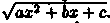 Выделив под радикалом полный квадрат и сделав подстановку Выделив под радикалом полный квадрат и сделав подстановку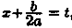 , интегралы указанного типа приводятся к интегралам уже pасcмoтpeннoгo типа, т. е. к интегралам типа , интегралы указанного типа приводятся к интегралам уже pасcмoтpeннoгo типа, т. е. к интегралам типа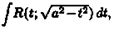 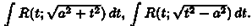 Эти интегралы можно вычислить с помощью соответствующих тригонометрических подстановок. Эти интегралы можно вычислить с помощью соответствующих тригонометрических подстановок.
Пример
Найти интеграл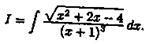
Решение: Так как х2
+2х-4=(х+1)2
-5, то х+1=t, x=t-1, dx=dt. Поэтому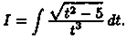 Положим Положим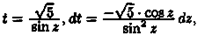 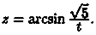
Тогда
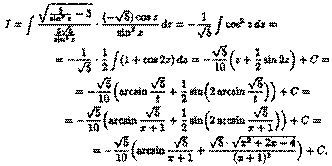
Замечание: Интеграл типа 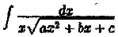 целессooбразно находить с помощью подстановки х=1/t. целессooбразно находить с помощью подстановки х=1/t.
Интегрирование дифференциального бинома
Интегралы типа(называемые интегралами от дифференциального бинома),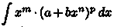 где а, b - действительные числа; m, n, р - рациональные числа, берутся лишь в случае, когда хотя бы одно из чисел р, (m+1)/n или (m+1)/n+р является целым. где а, b - действительные числа; m, n, р - рациональные числа, берутся лишь в случае, когда хотя бы одно из чисел р, (m+1)/n или (m+1)/n+р является целым.
Рационализация интеграла в этих случаях осуществляется следующими подстановками:
1) если р - целое число, то подстановка х=tk
, где k - наименьшее общее кратное знаменателей дробей m и n;
2) если (m+1)/n - целое число, то подстановка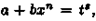 где s —знаменатель дроби р; где s —знаменатель дроби р;
3) если (m+1)/n+р - целое число, то подстановка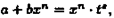 где s - знаменатель дpоби р. где s - знаменатель дpоби р.
Во всех остальных случаях интегралы типане выражаются через известные элементарные функции,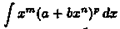 т. е. «не берутся». т. е. «не берутся».
Пример
Найти интеграл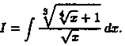
Решение: Так как
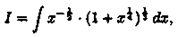
то 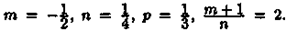
Поэтому делаем подстановку
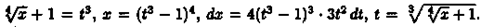
Таким образом,
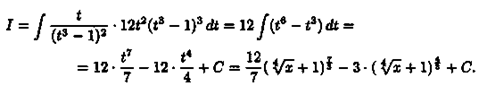
36.
Определенный интеграл. Формула Ньютона –Лейбница
Пусть функция у=ƒ(х) определена на отрезке [а; b], а < b. Выполним следующие действия.
1. С помощью точек х0
=а, x1,
х2, ...,
хn
= В (х0
<x1
< ...< хn
) разобьем отрезок [а, b] на n частичных отрезков [х0
;х1
], [x1
; х2
],..., [хn-1
,хn
] (см. рис. 167).

2. В каждом частичном отрезке [xi-1
;xi
], i = 1,2,...,n выберем произвольную точку сi
є [xi-1
; xi
] и вычислим значение функции в ней, т. е. величину ƒ(сi
).
3. Умножим найденное значение функции ƒ (сi
) на длину ∆xi
=xi
-xi-1
соответствующего частичного отрезка: ƒ (сi
) • ∆хi.
4. Составим сумму Sn
всех таких произведений:
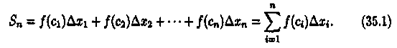 1. 1.
Сумма вида (1) называется интегральной суммой функции у = ƒ(х) на отрезке [а; b]. Обозначим через λ длину наибольшего частичного отрезка: λ = max ∆xi
(i = 1,2,..., n).
5. Найдем предел интегральной суммы (35.1), когда n → ∞ так, что λ→0.
Если при этом интегральная сумма Sn
имеет предел I, который не зависит ни от способа разбиения отрезка [а; b] на частичные отрезки, ни от выбора точек в них, то число I называется определенным интегралом от функции у = ƒ(х) на отрезке [а; b] и обозначается 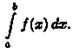 Таким образом, Таким образом,

Числа а и b называются соответственна нижним и верхним пределами интегрирования, ƒ(х) — подынтегральной функцией, ƒ(х) dx — подынтегральным выражением, х — переменной интегрирования, отрезок [а; b] — областью (отрезком) интегрирования.
Функция у=ƒ(х), для которой на отрезке [а; b] существует определенный интеграл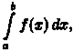 называется интегрируемой на этом отрезке. называется интегрируемой на этом отрезке.
Сформулируем теперь теорему существования определенного интеграла.
Теорема Коши. Если функция у = ƒ(х) непрерывна на отрезке [а; b], то определенный интеграл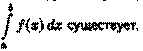
Отметим, что непрерывность функции является достаточным условием ее интегрируемости. Однако определенный интеграл может существовать и для некоторых разрывных функций, в частности для всякой ограниченной на отрезке функции, имеющей на нем конечное число точек разрыва.
Укажем некоторые свойства определенного интеграла, непосредственно вытекающие из его определения (35.2).
1. Определенный интеграл не зависим от обозначения переменной интегрирования:
Это следует из того, что интегральная сумма (35.1), а следовательно, и ее предел (35.2) не зависят от того, какой буквой обозначается аргумент данной функции.
2. Определенный интеграл с одинаковыми пределами интегрирования равен нулю: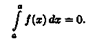
3. Для любого действительного числа с.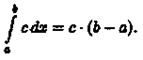
Пусть функция у = ƒ(х) интегрируема на отрезке [а; b].
Теорема
Если функция у = ƒ(х) непрерывна на отрезке [а; b] и F(x) — какая-либо ее первообразная на [а; b] (F'(x) = ƒ(х)), то имеет место формула
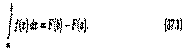
Разобьем отрезок [а;b] точками а = x0
, x1
,..., b = xn
(x0
< x1
< ...< хn
) на n частичных отрезков [x0
;x1
], [x1
;x2
],..., [xn-1
;xn
], как это показано на рис.
Рассмотрим тождество
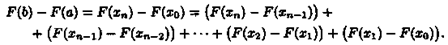
Преобразуем каждую разность в скобках по формуле Лагранжа
ƒ(b)-ƒ(а) = ƒ'(с)*(b-а).
Получим
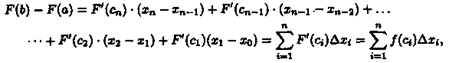
т. е.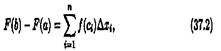 1
. 1
.
где ci
есть некоторая точка интервала (xi-1
; xi
). Так как функция у = ƒ(х) непрерывна на [а; b], то она интегрируема на [а; b]. Поэтому существует предел интегральной суммы, равный определенному интегралу от ƒ (х) на [а ;b].
Переходя в равенстве (1) к пределу при λ = max ∆xi
→0, получаем
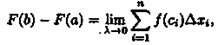
т. е.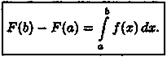
Равенство 1) называется формулой Ньютона-Лейбница. Если ввести обозначение F(b)- F(a) = F(x)|a
b
,
то формулу Ньютона-Лейбница (37.1) можно переписать так:
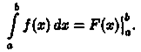
Формула Ньютона-Лейбница дает удобный способ вычисления определенного интеграла. Чтобы вычислить определенный интеграл от непрерывной функции ƒ (х) на отрезке [а; b], надо найти ее первообразную функцию F(x) и взять разность F(b)- F(a) значений этой первообразной на концах отрезка [a;b].
Например,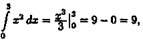
а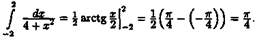
Пример
Вычислить интеграл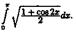
Решение:
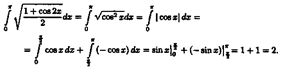
37.
Свойства определенного интеграла.
Рассмотрим основные свойства определенного интеграла, считая подынтегральную функцию интегрируемой на отрезке [a;b]. При выводе свойств будем использовать определение интеграла и формулу Ньютона-Лейбница.
1. Если с — постоянное число и функция ƒ(х) интегрируема на [a;b], то
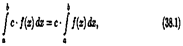 1. 1.
т. е. постоянный множитель с можно выносить за знак определенного интеграла.
Составим интегральную сумму для функции с • ƒ(х). Имеем:
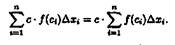
Тогда Отсюда вытекает, что функция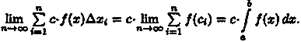 с • ƒ(х) интегрируема на [а; b] и справедлива формула (1). с • ƒ(х) интегрируема на [а; b] и справедлива формула (1).
2. Если функции ƒ1
(х) и ƒ2
(х) интегрируемы на [а;b], тогда интегрируема на [а; b] их сумма u
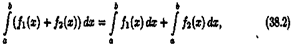 2. 2.
т. е. интеграл от суммы равен сумме интегралов.
▼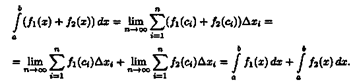
Свойство 2 распространяется на сумму любого конечного числа слагаемых.
3.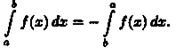
Это свойство можно принять по определению. Это свойство также подтверждается формулой Ньютона-Лейбница.
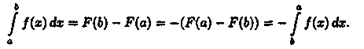
4. Если функция ƒ(х) интегрируема на [а; b] и а < с < b, то
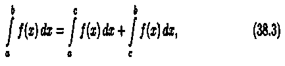 3. 3.
т. е. интеграл по всему отрезку равен сумме интегралов по частям этого отрезка. Это свойство называют аддитивностью определенного интеграла (или свойством аддитивности).
При разбиении отрезка [а;b] на части включим точку с в число точек деления (это можно сделать ввиду независимости предела интегральной суммы от способа разбиения отрезка [а; b] на части). Если с = хm
, то интегральную сумму можно разбить на две суммы:
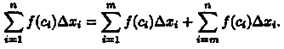
Каждая из написанных сумм является интегральной соответственно для отрезков [а; b], [а; с] и [с; b]. Переходя к пределу в последнем равенстве при n → ∞ (λ → 0), получим равенство (3).
Свойство 4 справедливо при любом расположении точек а, b, с (считаем, что функция ƒ (х) интегрируема на большем из получающихся отрезков).
Так, например, если а < b < с, то
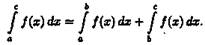
Отсюда
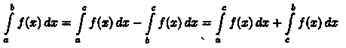
(использованы свойства 4 и 3).
5. «Теорема о среднем». Если функция ƒ(х) непрерывна на отрезке [а; b], то существует тонка с є [а; b] такая, что
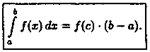
По формуле Ньютона-Лейбница имеем
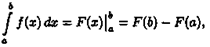
где F'(x) = ƒ(х). Применяя к разности F(b)-F(a) теорему Лагранжа (теорему о конечном приращении функции), получим
F(b)-F(a) = F'(c)•(b-а) = ƒ(с)•(b-а).
Число называется средним значением функции ƒ(х) на отрезке [а; b]. называется средним значением функции ƒ(х) на отрезке [а; b].
6. Если функция ƒ (х) сохраняет знак на отрезке [а; b], где а < b, то интеграл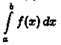 имеет тот же знак, что и функция. Так, если ƒ(х)≥0 на отрезке [а; b], то имеет тот же знак, что и функция. Так, если ƒ(х)≥0 на отрезке [а; b], то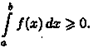
По «теореме о среднем» (свойство 5)

где с є [а; b]. А так как ƒ(х) ≥ 0 для всех х Î [а; b], то и
ƒ(с)≥0, b-а>0.
Поэтому ƒ(с)•(b-а) ≥ 0, т. е.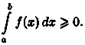 ▲ ▲
7. Неравенство между непрерывными функциями на отрезке [а; b], (a<b) можно интегрировать. Так, если ƒ1
(x)≤ƒ2
(х) при х є [а;b], то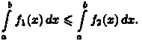
Так как ƒ2
(х)-ƒ1
(x)≥0, то при а < b, согласно свойству 6, имеем
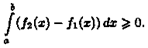
Или, согласно свойству 2,
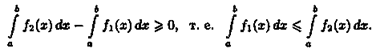
Отметим,что дифференцировать неравенства нельзя.
8. Оценка интеграла. Если m и М — соответственно наименьшее и наибольшее значения функции у = ƒ (х) на отрезке [а; b], (а < b), то
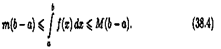 4. 4.
Так как для любого х є [а;b] имеем m≤ƒ(х)≤М, то, согласно свойству 7, имеем
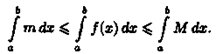
Применяяк крайним интегралам свойство 5, получаем
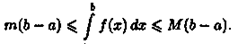
9. Модуль определенного интеграла не превосходит интеграла от модуля подынтегральной функции:
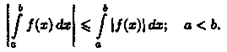
▼Применяя свойство 7 к очевидным неравенствам -|ƒ(х)|≤ƒ(х)≤|ƒ(х)|, получаем
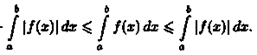
Отсюда следует, что
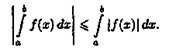
10. Производная определенного интеграла по переменному верхнему пределу равна подынтегральной функции, в которой переменная интегрирования заменена этим пределом, т. е.

По формуле Ньютона-Лейбница имеем:
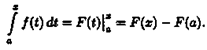
Следовательно,
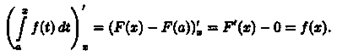
Это означает, что определенный интеграл с переменным верхним пределом есть одна из первообразных подынтегральной функции.
38.
Замена переменной и интегрирование по частям в определенном интеграле.
Пусть для вычисления интеграла от непрерывной функции от непрерывной функции
сделана подстановка х = φ(t).
Теорема 39.1. Если:
1) функция х = φ(t) и ее производная х' = φ'(t) непрерывны при t є [а;β];
2) множеством значений функции х = φ(t) при t є [а,β] является отрезок [а; b];
3) φ(а)=а и φ(β)=b.
то
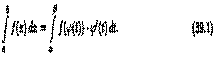 1. 1.
Пусть F(x) есть первообразная для ƒ(х) на отрезке [а;b]. Тогда по формуле Ньютона-Лейбница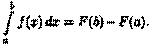
Так как (F(φ(t))' = f(φ(t)) - φ'(t), то F(φ(t)) является первообразной для функции f(φ(t)) -φ'(t), t Î [а;β]. Поэтому по формуле Ньютона—Лейбница имеем
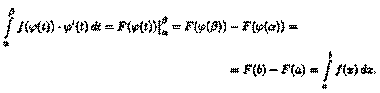 ▲ ▲
Формула 1) называется формулой замены переменной в определенном интеграле. Отметим, что:
1) при вычислении определенного интеграла методом подстановки возвращаться к старой переменной не требуется;
2) часто вместо подстановки х = φ(t) применяют подстановку t = g(x);
3) не следует забывать менять пределы интегрирования при замене переменных!
Пример.
Вычислить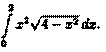
Решение: Положим х = 2 sin t, тогда dx = 2 cos t dt. Если х=0, то t = 0; если x = 2, то t =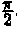 . Поэтому . Поэтому
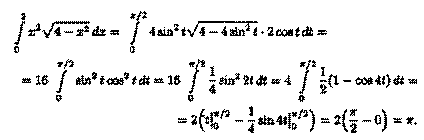
Интегрирование по частям
Теорема
. Если функции u = u(х) и v = v(x) имеют непрерывные производные на отрезке [а; b], то имеет место формула
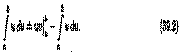 2. 2.
На отрезке [а; b] имеет место равенство (uv)' = u'v+uv'. Следовательно, функция uv есть первообразная для непрерывной функции u'v+uv'. Тогда по формуле Ньютона-Лейбница имеем:
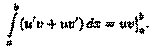
Следовательно,
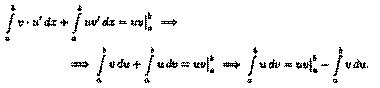
Формула (.2) называется формулой интегрирования по частям для определенного интеграла
.
Пример.
Вычислить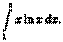
Решение: Положим

Применяя формулу 2), получаем
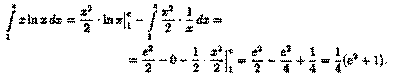
39.
Дифференциальные уравнения первого порядка. Общее и частное решения.
Обыкновенным дифференциальным уравнением называется уравнение, связывающее между собой значения независимой переменной x
, неизвестной функции y
= f
(x
) и её производных (или дифференциалов):
 ; (1) ; (1)
(все три переменные x
, y
, F
- действительны).
Опр
. Порядком
уравнения называется максимальный порядок n
входящей в него производной (или дифференциала).
Пример: y
(4)
– y
+ x
= 0 - уравнение четвёртого порядка.
Уравнение вида F(x, y, y/) = 0 называется уравнением первого порядка.
В простейших случаях оно может быть разрешено относительно у/ = f(x,y).
Общее решение имеет вид у = j(х,С), где С - константа.
Геометрически общее решение представляет собой семейство интегральных кривых.
Интегральные кривые обладают тем свойством, что все касательные в точке М(х,у) имеют наклон tga = f ’(x,y).
Если задать точку М0(х0,у0), через которую должна проходить интегральная кривая, то это требование называется начальным условием y = у0, х = х0 и тогда
у0 = j(х0,С0).
Определяется С - константа; в результате получаем частное интегральное решение у = j(х,С0).
В этом состоит задача Коши.
Опр
. Частным решением
уравнения (1) на интервале (a
, b
) (конечном или бесконечном) называется любая n
раз дифференцируемая функция  , удовлетворяющая этому уравнению, т.е. обращающая уравнение на этом интервале в тождество. , удовлетворяющая этому уравнению, т.е. обращающая уравнение на этом интервале в тождество.
Так, функция y
(x
) = ex
+ x
обращает уравнение : y
(4)
– y
+ x
= 0 в тождество на всей числовой оси (y
(4)
(x
) = ex
; ex
–(ex
+x
) + x
= 0), т.е. является частным решением этого уравнения. Любое уравнение порядка  имеет множество частных решений (частным решением приведённого уравнения является и функция y
(x
) = sin(x
) + x
). Процедуру решения дифференциального уравнения часто называют интегрированием уравнения, при этом интегрировать приходится в общем случае ровно n
раз, и при каждом интегрировании в решение входит очередная произвольная постоянная. имеет множество частных решений (частным решением приведённого уравнения является и функция y
(x
) = sin(x
) + x
). Процедуру решения дифференциального уравнения часто называют интегрированием уравнения, при этом интегрировать приходится в общем случае ровно n
раз, и при каждом интегрировании в решение входит очередная произвольная постоянная.
Опр. Общим решением (общим интегралом) уравнения
(1) называется такое соотношение
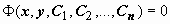 ; (2) ; (2)
что: 1. Любое решение (2) 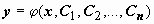 относительно y
(для набора постоянных C
1
, C
2
, …, Cn
из некоторой области n
-мерного пространства) - частное решение уравнения (1); относительно y
(для набора постоянных C
1
, C
2
, …, Cn
из некоторой области n
-мерного пространства) - частное решение уравнения (1);
2. Любое частное решение уравнения (1) может быть получено из (2) при некотором наборе постоянных C
1
, C
2
, …, Cn
.
Мы будем в основном рассматривать дифференциальные уравнения в форме, разрешённой относительно старшей производной:
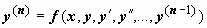 ; ;
и получать общее решение в форме
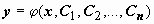 ; ;
решённой относительно неизвестной функции.
обыкновенным дифференциальным уравнением первого порядка называется уравнение
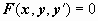 ; ;
где x
- независимая переменная, y
(x
) - неизвестная функция. В форме, разрешённой относительно производной, уравнение первого порядка записывается так:
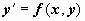 ; ;
Если пользоваться другим обозначением производной, то можно записать (6) как
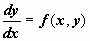 ; ;
Общее решение (общий интеграл) уравнения при n
= 1 имеет вид  или или 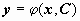 . .
40.
Уравнения с разделенными и разделяющимися переменными.
Уравнения с разделенными переменными
Так называются уравнения вида удовлетворяющее начальному условию
 f
(x
) dx
+ g
(y
) dy
= 0. f
(x
) dx
+ g
(y
) dy
= 0.
Пусть y
(x
) - решение этого уравнения, т.е. f
(x
)dx
+ g
(y
(x
))dy
(x
) = 0. Интегрируя это тождество, получим 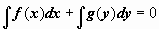 - общий интеграл (общее решение) этого уравнения. - общий интеграл (общее решение) этого уравнения.
Пример: решить задачу Коши 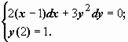 Исходное уравнение - с разделёнными переменными, интегрируя его, получим Исходное уравнение - с разделёнными переменными, интегрируя его, получим 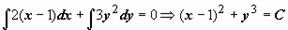 . Соотношение (x
-1)2
+ y
3
= C
- общее решение (общий интеграл) уравнения; для того, чтобы найти частное решение, удовлетворяющее начальному условию, надо подставить в общее решения данные значения x
0
и y
0
, и найти значение постоянной C
на этом решении: (2-1)2
+ 13
= 2 . Соотношение (x
-1)2
+ y
3
= C
- общее решение (общий интеграл) уравнения; для того, чтобы найти частное решение, удовлетворяющее начальному условию, надо подставить в общее решения данные значения x
0
и y
0
, и найти значение постоянной C
на этом решении: (2-1)2
+ 13
= 2  C
= 2. Таким образом, решение поставленной задачи: (x
-1)2
+ y
3
= 2. C
= 2. Таким образом, решение поставленной задачи: (x
-1)2
+ y
3
= 2.
Уравнения с разделяющимися переменными.
Так называются уравнения вида
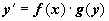 или или
f
1
(x
) g
1
(y
) dx
+ f
2
(x
) g
2
(y
) dy
= 0
Эти уравнения легко сводятся к уравнению с разделёнными переменными:
Записываем уравнение (11) в форме 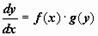 , затем делим на g
(y
) и умножаем на dx
: , затем делим на g
(y
) и умножаем на dx
: 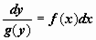 . 1. . 1.
Уравнение (1) делим на f
2
(x
) g
1
(y
): 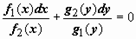 . .
Эти уравнения - с разделёнными переменными. Интегрируя, получим общие интегралы:
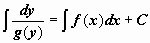 . . 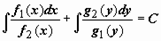 . .
В обоих случаях возможна потеря решений: деление на функцию может привести к уравнению, которое неэквивалентно данному.
Если функция g
(y
) имеет действительные корни y
1
, y
2
, y
3
, …, то функции y
= y
1
, y
= y
2
,
y
= y
3
, …, очевидно, являются решениями исходного уравнения. Если функция f
2
(x
) имеет действительные корни x
1
, x
2
, x
3
, …, функция g
1
(y
) имеет действительные корни y
1
, y
2
, y
3
, …, то функции x
= x
1
, x
= x
2
, x
= x
3
, …, y
= y
1
, y
= y
2
, y
= y
3
, … являются решениями исходного уравнения.
В обоих случаях эти решения могут содержаться в общем решении, но могут и не содержаться в нём; последнее может случиться, если на этих решениях нарушаются условия теоремы существования и единственности решения задачи Коши.
Пример:  . .
При такой форме записи общего интеграла решение y
= 1 потеряно. Можно преобразовать общее решение к виду, который содержит это решение. Переобозначим постоянную C
как ln|C
1
|: 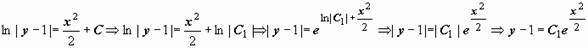 . Вернёмся к обозначению постоянной интегрирования C
; общее решение . Вернёмся к обозначению постоянной интегрирования C
; общее решение 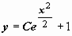 содержит частное решение y
= 1 при C
= 0. содержит частное решение y
= 1 при C
= 0.
41.
Однородные дифференциальные уравнения первого порядка.
Рассмотрим многочлен
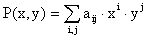 ,
,
он называется однородным степени n
, если все его члены имеют один и тот же порядок n, то есть для каждого аij
×хi
×уj
имеем i+j=n.
Определение 1
. Функция Р(х,у) называется однородной степени n
, если для любого k - числа - имеет место тождество
Р(k×х,k×у) = kn
×P(x,y).
Пусть дано уравнение
Р(х,у)dx+Q(x,y)dy=0. (1.8)
Если P(x,y),Q(x,y) - однородные функции одной и той же степени n, тогда (1.8) является однородным уравнением первого порядка
.
Для решения таких уравнений пользуются подстановкой 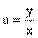 или
или 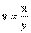 , которая приводит к уравнению с разделяющимися переменными.
, которая приводит к уравнению с разделяющимися переменными.
Пример
.
х2
+у2
-2×х×у×у/
=0.
Предположим, что х×у ¹ 0. Тогда
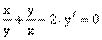 .
.
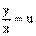 следовательно, у = u×x , а отсюда dy = udx+xdu
следовательно, у = u×x , а отсюда dy = udx+xdu
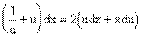
После приведения подобных и перегруппировки членов имеем
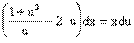
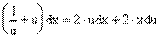
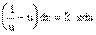
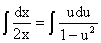 Þ
Þ 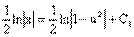
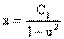 следовательно, x2
-y2
=C1
×x - решение.
следовательно, x2
-y2
=C1
×x - решение.
Сделаем проверку
1. Если х = 0 тогда C0
= 0 и, следовательно x2
= y2
.
2. 1-u2
= 0 .
Пусть теперь однородное дифференциальное уравнение имеет вид
у/
= f(x,y) или 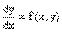 .
.
Тогда dy=f(x,y)dx, то есть при dy стоит коэффициент, равный единице, то есть имеем однородную функцию нулевой степени: следовательно, f(x,y) должна быть однородной функцией нулевой степени.
42.
Линейные дифференциальные уравнения первого порядка.
Линейное уравнение имеет вид:
а(х)×у/
+ b(х)×y + c(x) = 0, (1.9)
где а(х), b(x), c(x) - заданные функции.
Если а(х) ¹ 0, то это уравнение можно записать в приведенном виде:
у/
+ Р(х)×у = f(x), (1.10)
где  ,
, 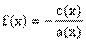 ,
,
тогда f(x) - свободный член.
Пусть Р(х) и f(x) в (1.10) непрерывны на (a,b).
Будем искать решение в виде y = u×v, где u - ненулевое решение соответствующего однородного уравнения
u/
+ P(x)×u = 0, (1.11)
a v - неизвестная функция. Тогда
y/
= u/
×v + v/
×u. (1.12)
Подставим в (1.10) эти выражения. Получим
u/
×v + v/
×u + P(x)×u×v = f(x) (1.13)
v × (u/
+P(x)× u) + u×v/
= f(x)
Учитывая, что имеет место (1.11), получим
u×v/
= f(x). (1.14)
Следует u подобрать так, чтобы коэффициент при v был равен нулю.
Из (1.11) и (1.14) находим u и v, подставляем в y = u×v, причем u есть конкретное решение, отличное от нуля.
Пример.
Необходимо найти частное решение
x×y/
-y = x2
.
Начальные условия:
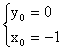 .
.
Пусть у = 0 при х = -1.
Искомое решение запишем в виде y = u×v.
y/
= u/
×v + v/
×u.
Подставим в уравнение, имеем
x×u/
×v + x×v/
×u - u×v = x2
.
После приведения подобных имеем
v×(x×u/
- u) + x×u×v/
= x2
.
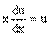 Þ
Þ  следовательно, lnu = lnx + lnC0
.
следовательно, lnu = lnx + lnC0
.
Если С0
= 1 , значит, u = x.
Но тогда
x2
×v/
= x2
и v = x + C1
.
y = x
×
( x + C1
) = x2
+ C1
×
x - общее решение.
А если у0
= 0 , то получим 1 + С1
×(-1) откуда С1
= 1.
у = х2
+ х - частное решение
.
Пример.
(х + у)×у/
= 1.
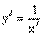 ,
, 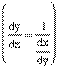 .
.
Пусть
x = u×v, тогда 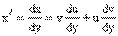 и
и
v×u/
+ u×v/
= x + y.
Учитывая, что х = u×v, имеем
v×(u/
-v) + u×v/
= y
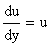 следовательно, lnu = y, u = ey
,
следовательно, lnu = y, u = ey
,
Так как 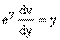 , то имеем
, то имеем 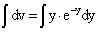 .
.
Далее
v = -y×e-y
- e-y
+ C.
x = u×v = -y-1 + C×ey
- общее решение.
y = -y-1 + C×ey
начальные условия:
у0
= 0, х0
= 2.
2 = -1 + С Þ С = 1
х + у + 1 = еу
- частное решение.
43.
Ряды. Сходимость рядов. Свойства сходящихся рядов.
Бесконечным числовым рядом
называется выражение
u1
+u2
+...+un
+... ,
(1)
содержащее неограниченное число членов, где u1
, u2
, u3
, ... , un
, ...
- бесконечная числовая последовательность; un
называется общим членом ряда
.
Для составления ряда нужно знать закон образования общего члена.
Например, если un
= 2*n+1
, то ряд имеет вид:
3, 5, 7, 9, ..., 501, 503, ..., n*2+1
Если un
= (-1)n
, то ряд имеет вид:
-1, +1, -1, +1, ..., -1, +1, ..., (-1)n
Сумма первых n
членов ряда обозначается символом Sn
и называется частичной суммой
этого ряда. Таким образом,
Sn
= u1
+ u2
+ ... + u n
или, короче,
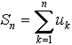
Определение:
Ряд называется сходящимся
, если сумма первых его n
членов при n
®¥ стремится к конечному пределу S
, называемому суммой
ряда.
Если ряд (1)
сходится, т.е. имеет сумму S
, то пишут
S = u1
+ u2
+ ... + u n
+ ...
Если же при n
®¥ сумма Sn
не имеет предела или
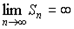
то ряд (1)
называется расходящимся
и не имеет суммы.
Типичным примером сходящегося ряда может служить ряд, полученный из бесконечно убывающей геометрической прогрессии
a + aq + aq 2
+ aq 3
+ ... + aq n-1
+ ...,
(2)
где -1 < q
< 1
Действительно, для этого ряда
Sn
= a + aq + aq 2
+ aq 3
+ ... + aq n-1
=
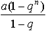
При n
®¥ qn
®0
(так как | q
|<1), поэтому
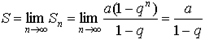
и ряд (2)
будет сходящимся. Таким образом можно написать
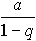 = a + aq + aq 2
+ aq 3
+ ... + aq n-1
+ ... . = a + aq + aq 2
+ aq 3
+ ... + aq n-1
+ ... .
Если q = 1
, то ряд (2)
имеет вид
a + a + a + a + ... + a + ... .
(3)
Сумма Sn
первых его n
членов, равная na
, по абсолютной величине неограниченно возрастает при неограниченном возрастании числа n
. Таким образом, ряд (3)
- расходящийся.
Если q = -1
, то ряд (2)
примет вид
a - a + a - a + a - a +... +(-1)n-1
a + ... .
(4)
Ясно, что для этого ряда S2n
=0 , S2n-1
=a.
т.е.сумма четного числа первых 2n
членов ряда (4) стремится к нулю, а сумма нечетного числа первых 2n-1
его членов стремится к a
.
Отсюда следует, что ряд (4) расходится, так как в сходящемся ряде как S2n
так и S2n-1
стремятся к одному и тому же пределу S
.
Ясно, что если | q
|>1, то ряд (2)
является также расходящимся.
44.
Необходимый признак сходимости. Гармонический ряд.
Теорема:
Пусть числовой ряд
u1
+u2
+...+un
+... ,
(1)
сходится, а S - его сумма. Тогда при неограниченном возрастании числа n членов ряда его общий член un
стремится к нулю
Доказательство.
Из условия теоремы имеем
 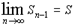
Так как
Sn
- Sn-1
= un
то
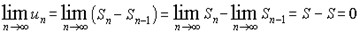
Следует отметить, что этот признак является лишь необходимым, но не достаточным признаком сходимости ряда, так как можно указать ряд, для которого выполняется равенство
 , ,
а он, однако не является сходящимся.
Так гармонический ряд
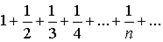 , ,
для которого
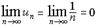 , ,
расходится.
Но согласно доказанному необходимому признаку сходимости ряда, если
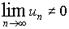 , ,
то ряд (1)
расходится.
В самом деле, если бы он сходился, то
равнялся бы нулю.
Таким образом, доказанная нами теорема иногда позволяет, не вычисляя суммы Sn
, сделать заключение о расходимости того или иного ряда. Например, ряд
 , ,
расходится, так как
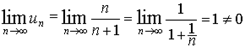
45.
Достаточные признаки сходимости рядов с положительными членами.
Признаки сравнения
Если 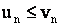 , и ряд
, и ряд 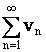 сходится, то сходится и ряд
сходится, то сходится и ряд 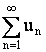 .
.
Если 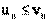 , и ряд
, и ряд 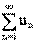 расходится, то расходится и ряд
расходится, то расходится и ряд 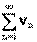 .
.
Признаки сравнения можно сформулировать в такой форме:
Если заданы ряды 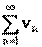 ,
, 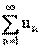 и существует
и существует 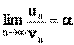
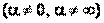 , то ряды
, то ряды 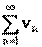 и
и 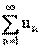 сходятся либо расходятся одновременно.
сходятся либо расходятся одновременно.
Пример
:
1
. Исследуем сходимость ряда 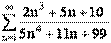 . Очевидно, что
. Очевидно, что 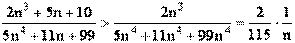 .
.
Так как гармонический ряд 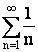 расходится, то и ряд
расходится, то и ряд 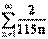 также расходящийся, и, согласно признаку сравнения, данный ряд
также расходящийся, и, согласно признаку сравнения, данный ряд 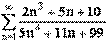 расходится.
расходится.
2
. Исследовать сходимость ряда 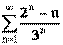 . Имеем:
. Имеем: 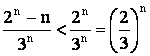 .
.
Ряд 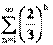 сходится как сумма геометрической прогрессии со знаменателем
сходится как сумма геометрической прогрессии со знаменателем 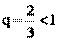 . Следовательно, согласно признаку сравнения ряд
. Следовательно, согласно признаку сравнения ряд 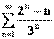 сходится.
сходится.
Признак Д’Аламбера
Если существует 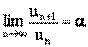 то:
то:
- при 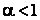 ряд
ряд 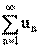 сходится;
сходится;
- при 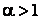 ряд
ряд 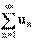 расходится.
расходится.
Радикальный признак Коши
Если существует 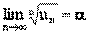 то:
то:
- при  ряд
ряд  сходится;
сходится;
- при  ряд
ряд 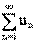 расходится.
расходится.
Интегральный признак Коши
Пусть задан ряд 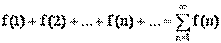 , члены которого являются значениями непрерывной, положительной и монотонно убывающей функции
, члены которого являются значениями непрерывной, положительной и монотонно убывающей функции 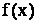 на промежутке
на промежутке  . Тогда ряд
. Тогда ряд 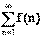 сходится, если сходится несобственный интеграл
сходится, если сходится несобственный интеграл 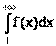 .
.
Если же 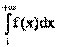 расходится, то ряд
расходится, то ряд 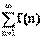 также будет расходящимся.
также будет расходящимся.
46.
Ряды с членами произвольного знака. Признак Лейбница.
Ряд называется знакопеременным, если он содержит бесконечное множество как положительных, так и отрицательных членов. Знакопеременный ряд называется знакочередующимся, если за каждым положительным членом следует отрицательный и за каждым отрицательным следует положительный. Для знакочередующихся рядов имеется достаточный признак сходимости Лейбница: если в знакочередующемся ряде члены убывают по абсолютной величине и общий член стремится к нулю, то ряд сходится. Для общего случая знакопеременных рядов имеется следующий достаточный признак; если сходится ряд из абсолютных величин членов данного ряда, то сходится и данный ряд; в этом случае сходимость называют абсолютной. Приведенный признак не является необходимым, т. е. из сходимости знакопеременного ряда не следует сходимость ряда из абсолютных величин. Сходимость знакопеременного ряда называется условной, если этот ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится. Абсолютно сходящиеся ряды обладают тем свойством, что над ними можно совершать операции, аналогичные операциям над конечными суммами, некоторые из этих операций к условно сходящимся рядам не применимы.
Признак Лейбница
(достаточный признак сходимости знакочередующихся
рядов)
Ряд 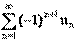 сходится, если:
сходится, если:
- 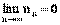 ;
;
- 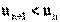 .
.
Знакопеременный ряд 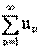 называют абсолютно сходящимся
, если сходится ряд
называют абсолютно сходящимся
, если сходится ряд 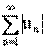 .
.
Если ряд 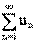 сходится, а ряд
сходится, а ряд 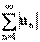 расходится, то ряд
расходится, то ряд 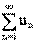 называют сходящимся условно
.
называют сходящимся условно
.
Очевидно, что если ряд 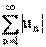 сходится, то ряд
сходится, то ряд 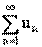 также сходится. Обратное утверждение в общем случае неверно.
также сходится. Обратное утверждение в общем случае неверно.
47.
Степенной ряд. Теорема Абеля. Радиус сходимости степенного ряда.
Важный частный случай функциональных рядов представляют собой степенные ряды
, т.е. ряды вида 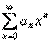 или, в более общем случае,
или, в более общем случае, 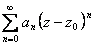 . Поскольку при замене
. Поскольку при замене 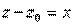 ряд
ряд 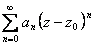 переходит в ряд
переходит в ряд 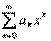 , достаточно рассмотреть эти последние ряды.
, достаточно рассмотреть эти последние ряды.
Теорема 1.
Если степенной ряд 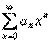 сходится в точке
сходится в точке 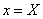 , то он сходится абсолютно для любого значения
, то он сходится абсолютно для любого значения 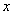 такого, что
такого, что 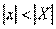 .
.
Доказательство.
Поскольку 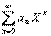 - сходится,
- сходится, 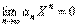 . Следовательно,
. Следовательно, 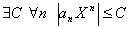 . (Действительно, взяв
. (Действительно, взяв 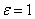 , получим, что при
, получим, что при 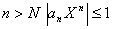 . Тогда в качестве
. Тогда в качестве 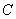 можно взять наибольшее из конечного набора чисел
можно взять наибольшее из конечного набора чисел 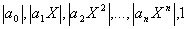 ). Тогда
). Тогда 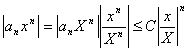 . Так как
. Так как 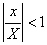 , прогрессия
, прогрессия 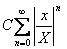 сходится. Значит, по первой теореме о сравнении, сходится ряд
сходится. Значит, по первой теореме о сравнении, сходится ряд 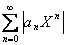 , т.е. исходный ряд абсолютно сходится.
, т.е. исходный ряд абсолютно сходится.
Эта теорема позволяет выяснить структуру множества, на котором сходится степенной ряд.
Во-первых, очевидно, что любой степенной ряд сходится в точке  . Кроме того, есть ряды, которые сходятся только
в этой точке, например, ряд
. Кроме того, есть ряды, которые сходятся только
в этой точке, например, ряд 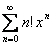 .
.
Если же ряд сходится в точках, отличных от 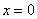 , то возможны два случая.
, то возможны два случая.
В первом из них множество чисел 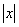 таких, что ряд сходится в точке
таких, что ряд сходится в точке 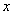 , неограничено сверху. Тогда ряд абсолютно сходится на всей числовой прямой, т.к.
, неограничено сверху. Тогда ряд абсолютно сходится на всей числовой прямой, т.к. 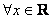 выберем
выберем 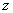 так, чтобы, во-первых,
так, чтобы, во-первых, 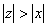 и, во-вторых, ряд
и, во-вторых, ряд 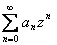 сходился. Тогда, по теореме 1, ряд
сходился. Тогда, по теореме 1, ряд 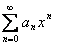 абсолютно сходится.
абсолютно сходится.
Во втором случае множество чисел 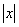 таких, что ряд
таких, что ряд 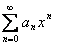 сходится, ограничено сверху. Обозначим через
сходится, ограничено сверху. Обозначим через  точную верхнюю грань этого множества. Число
точную верхнюю грань этого множества. Число  называется радиусом сходимости
ряда. Из определения
называется радиусом сходимости
ряда. Из определения 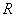 следует, что:
следует, что:
1. Если 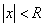 , то ряд
, то ряд 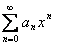 абсолютно сходится;
абсолютно сходится;
2. Если 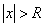 , то ряд
, то ряд 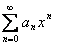 расходится.
расходится.
В случае, когда ряд сходится на всей числовой прямой  , полагают
, полагают 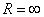 .
.
В точках 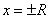 общего утверждения о сходимости сделать нельзя (т.е. бывают ряды, сходящиеся в обеих этих точках, бывают – сходящиеся лишь в одной из них, бывают – расходящиеся в обеих точках. Примеры будут приведены ниже).
общего утверждения о сходимости сделать нельзя (т.е. бывают ряды, сходящиеся в обеих этих точках, бывают – сходящиеся лишь в одной из них, бывают – расходящиеся в обеих точках. Примеры будут приведены ниже).
Найдем формулы, с помощью которых можно вычислить 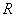 - радиус сходимости степенного ряда. Рассмотрим ряд
- радиус сходимости степенного ряда. Рассмотрим ряд 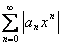 . Применим к его исследованию признак Даламбера.
. Применим к его исследованию признак Даламбера. 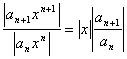 . Если существует
. Если существует 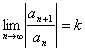 , и если
, и если  , то ряд сходится. Если же
, то ряд сходится. Если же 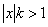 , то, начиная с некоторого места,
, то, начиная с некоторого места, 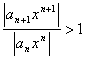 и общий член
и общий член 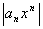 ряда
ряда 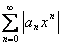 не стремится к 0, но тогда и общий член
не стремится к 0, но тогда и общий член 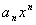 ряда
ряда 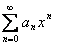 не стремится к 0 и ряд расходится.
не стремится к 0 и ряд расходится.
Иными словами, ряд сходится при 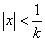 и расходится при
и расходится при 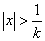 . Таким образом, число
. Таким образом, число 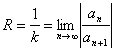 представляет собой радиус сходимости степенного ряда. (Если
представляет собой радиус сходимости степенного ряда. (Если 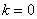 , то
, то 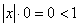 при всех
при всех 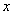 и ряд сходится на всей числовой прямой, что обозначается равенством
и ряд сходится на всей числовой прямой, что обозначается равенством 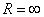 ).
).
Дадим другую формулу для радиуса сходимости. Применим к рассматриваемому ряду 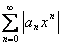 признак Коши.
признак Коши. 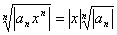 . Пусть существует
. Пусть существует 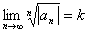 . Тогда, как и выше, при
. Тогда, как и выше, при 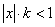 ряд сходится, а при
ряд сходится, а при 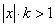 - расходится. Поэтому
- расходится. Поэтому 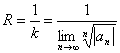 (при
(при 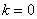 , разумеется,
, разумеется, 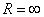 ).
).
Рассмотрим примеры.
Пример 1.
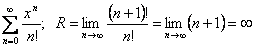 . Ряд абсолютно сходится на всей числовой прямой.
. Ряд абсолютно сходится на всей числовой прямой.
Пример 2.
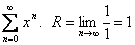 . В точках
. В точках 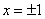 ряд, очевидно, расходится.
ряд, очевидно, расходится.
Пример 3.
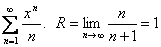 . В точке
. В точке 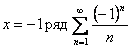 сходится по теореме Лейбница. В точке
сходится по теореме Лейбница. В точке 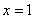 гармонический ряд
гармонический ряд  расходится.
расходится.
Пример 4.
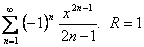 . В точках
. В точках 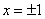 получается условно сходящийся ряд
получается условно сходящийся ряд 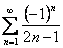 .
.
Пример 5.
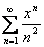 .
. 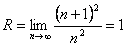 . В точках
. В точках 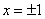 имеем ряд
имеем ряд 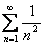 , который абсолютно сходится.
, который абсолютно сходится.
Теорема.
Степенной ряд 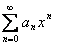 представляет собой функцию, непрерывную на
представляет собой функцию, непрерывную на  , где
, где 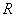 - радиус сходимости ряда.
- радиус сходимости ряда.
Доказательство.
Лемма.
Пусть 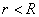 . Тогда
. Тогда 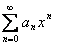 сходится на множестве
сходится на множестве 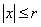 абсолютно и равномерно.
абсолютно и равномерно.
Доказательство.
Так как 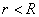 , ряд
, ряд 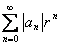 сходится. Так как
сходится. Так как 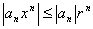 , можно применить теорему Вейерштрасса, из которой и следует утверждение леммы.
, можно применить теорему Вейерштрасса, из которой и следует утверждение леммы.
Замечание.
Лемма отнюдь не утверждает
равномерной сходимости степенного ряда на 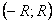 . Да это, вообще говоря, и неверно. Например, прогрессия
. Да это, вообще говоря, и неверно. Например, прогрессия 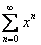 сходится на
сходится на 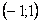 неравномерно
. Однако этот ряд сходится равномерно на любом
неравномерно
. Однако этот ряд сходится равномерно на любом 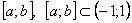 .
.
Пусть теперь 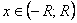 , т.е.
, т.е. 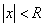 . Выберем
. Выберем 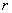 так, чтобы
так, чтобы 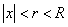 . Тогда, по доказанной лемме, ряд сходится на
. Тогда, по доказанной лемме, ряд сходится на 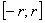 абсолютно и равномерно. Поскольку все функции
абсолютно и равномерно. Поскольку все функции 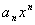 - непрерывные, сумма ряда есть непрерывная на
- непрерывные, сумма ряда есть непрерывная на  функция. Значит, эта функция непрерывна и в выбранной, произвольной точке
функция. Значит, эта функция непрерывна и в выбранной, произвольной точке  интервала
интервала  .
.
Следствие.
(Единственность степенного ряда). Пусть 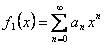 ,
, 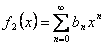 и в некоторой окрестности
и в некоторой окрестности 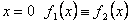 . Тогда
. Тогда 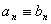 .
.
Доказательство.
При 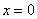 получаем:
получаем: 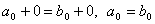 . Поэтому
. Поэтому 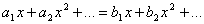 . При
. При 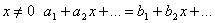 . В правой и левой частях стоят степенные ряды, а они, по-доказанному, есть непрерывные функции, поэтому равенство сохраняется при
. В правой и левой частях стоят степенные ряды, а они, по-доказанному, есть непрерывные функции, поэтому равенство сохраняется при 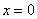 , откуда
, откуда 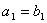 и т.д. (Отметим, что здесь существенно использована непрерывность
ряда в точке
и т.д. (Отметим, что здесь существенно использована непрерывность
ряда в точке 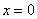 ).
).
Сформулируем без доказательства еще одну важную теорему.
Теорема.
(Абель). Если ряд  , имеющий сумму
, имеющий сумму 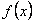 , сходится (хотя бы неабсолютно) при
, сходится (хотя бы неабсолютно) при 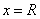 , то
, то 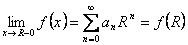 (т.е. сумма ряда непрерывна слева).
(т.е. сумма ряда непрерывна слева).
Теорема.
Для любого 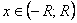
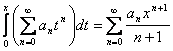 .
.
Доказательство.
Пусть 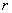 удовлетворяет неравенствам
удовлетворяет неравенствам  . Тогда степенной ряд сходится равномерно на
. Тогда степенной ряд сходится равномерно на  и его можно почленно проинтегрировать. Кроме того,
и его можно почленно проинтегрировать. Кроме того, 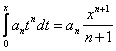 . Теорема доказана.
. Теорема доказана.
Теорема.
Для любого 
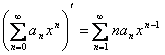 .
.
Доказательство.
Выберем 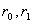 так, чтобы
так, чтобы 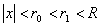 . По определению
. По определению 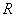 , ряд
, ряд 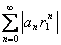 сходится. Поэтому
сходится. Поэтому 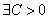 (см. доказательство теоремы 1):
(см. доказательство теоремы 1): 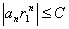 . Рассмотрим величину
. Рассмотрим величину 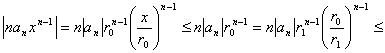
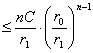 . По признаку Даламбера, ряд
. По признаку Даламбера, ряд 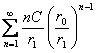 сходится, т.к.
сходится, т.к.  . Значит, мы оценили члены ряда
. Значит, мы оценили члены ряда 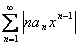 при
при 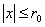 членами сходящегося ряда
членами сходящегося ряда 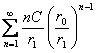 . Применяя теорему Вейерштрасса на
. Применяя теорему Вейерштрасса на 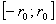 , получаем, что этот ряд равномерно сходится. Следовательно, почленное дифференцирование обосновано на отрезке
, получаем, что этот ряд равномерно сходится. Следовательно, почленное дифференцирование обосновано на отрезке 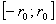 , а значит, и в точке
, а значит, и в точке 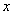 . Ввиду произвольности точки
. Ввиду произвольности точки 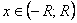 , теорема доказана.
, теорема доказана.
Важное замечание.
Из доказанных теорем вытекает, что при интегрировании и дифференцировании радиус сходимости не уменьшается
. Но увеличиться он также не может. Если бы, например, он увеличился и стал равен 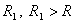 при интегрировании, мы продифференцировали бы этот полученный при интегрировании ряд и получили бы с одной стороны, ряд, совпадающий с исходным, а с другой стороны, имеющий радиус сходимости не меньший, чем
при интегрировании, мы продифференцировали бы этот полученный при интегрировании ряд и получили бы с одной стороны, ряд, совпадающий с исходным, а с другой стороны, имеющий радиус сходимости не меньший, чем 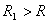 (по доказанному).
(по доказанному).
Итак, радиус сходимости степенного ряда не меняется при почленном интегрировании и дифференцировании.
Однако поведение в концевых точках 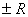 может меняться. Например, ряд
может меняться. Например, ряд 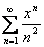 сходится на
сходится на 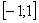 . При этом ряд
. При этом ряд 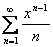 , получающийся из исходного дифференцированием, сходится только на
, получающийся из исходного дифференцированием, сходится только на 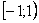 , а прогрессия
, а прогрессия 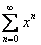 , получающаяся при дифференцировании ряда
, получающаяся при дифференцировании ряда 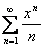 (сходящегося на
(сходящегося на 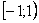 ), сходится на
), сходится на 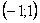 .
.
Рассмотрим теперь функцию 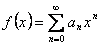 , представляемую степенным рядом в области его сходимости. Очевидно,
, представляемую степенным рядом в области его сходимости. Очевидно, 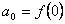 . Далее, последовательно применяем теорему о почленном дифференцировании ряда.
. Далее, последовательно применяем теорему о почленном дифференцировании ряда. 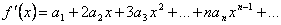 , откуда
, откуда 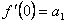 .
. 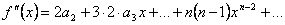 , откуда
, откуда 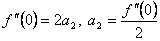 .
. 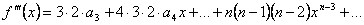 ,
, 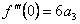 и т.д.
и т.д. 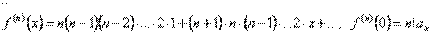 .
.
Следовательно, при всех 
 . Таким образом,
. Таким образом, 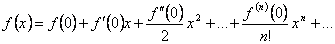 . Это можно сформулировать так: степенной ряд, сходящийся к
. Это можно сформулировать так: степенной ряд, сходящийся к  , представляет собой ряд Тейлора
для своей суммы
, представляет собой ряд Тейлора
для своей суммы  .
.
Если  имеет производные произвольного порядка в точке
имеет производные произвольного порядка в точке 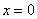 , то можно образовать соответствующий ей ряд Тейлора:
, то можно образовать соответствующий ей ряд Тейлора: 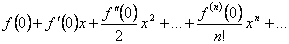 .
.
Важное замечание.
Не всегда этот ряд сходится к самой функции  . Например, нетрудно доказать, что функция
. Например, нетрудно доказать, что функция  имеет производные произвольного порядка в точке
имеет производные произвольного порядка в точке  и все они равны 0, т.е.
и все они равны 0, т.е. 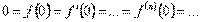 . Ряд Тейлора этой функции тождественно равен 0 и не совпадает с
. Ряд Тейлора этой функции тождественно равен 0 и не совпадает с 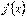 .
.
Необходимое и достаточное условие для того, чтобы ряд Тейлора функции 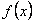 сходился к самой функции
сходился к самой функции 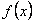 , можно сформулировать так: остаток
, можно сформулировать так: остаток 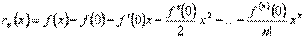 должен стремиться к 0 при
должен стремиться к 0 при  .
.
|