«УТВЕРЖДАЮ» «СОГЛАСОВАНО» Директор Федерального института Председатель Научнопедагогических измерений методического совета ФИПИ по математике

Единый государственный экзамен по МАТЕМАТИКЕ
Демонстрационный вариант КИМ 2009 г.
подготовлен Федеральным государственным научным учреждением
«ФЕДЕРАЛЬНЫЙ ИНСТИТУТ ПЕДАГОГИЧЕСКИХ ИЗМЕРЕНИЙ»

Единый государственный экзамен по МАТЕМАТИКЕ
Пояснения к демонстрационному варианту
При ознакомлении с Демонстрационным вариантом 2009 года следует иметь в виду, что задания, включённые в демонстрационный вариант, не отражают всех вопросов содержания, которые будут
проверяться с помощью вариантов КИМ в 2009 году
. Полный перечень вопросов, которые могут контролироваться на едином государственном экзамене 2009 года, приведен в кодификаторе, помещенном на сайте www.fipi.ru
.
Назначение демонстрационного варианта заключается в том, чтобы дать возможность любому участнику ЕГЭ и широкой общественности составить представление о структуре будущих КИМ, количестве заданий, их форме, уровне сложности: базовом, повышенном и высоком.
К каждому заданию с развернутым ответом (тип С), включенному в демонстрационный вариант, дается только одно из возможных
решений. Приведённые критерии оценки этих решений позволят составить представление о требованиях к полноте и правильности записи развёрнутого ответа.
Эти сведения позволят выпускникам выработать стратегию подготовки и сдачи ЕГЭ в соответствии с целями, которые они ставят перед собой.
Для правильной распечатки файла демонстрационного варианта по математике необходимо установить на компьютере программное обеспечение MathType версии не ниже 5.0.
Единый государственный экзамен по МАТЕМАТИКЕ
Демонстрационный вариант 2009 г.
Инструкция по выполнению работы
На выполнение экзаменационной работы по математике дается 4 часа (240 мин). Работа состоит из трех частей и содержит 26 заданий.
Часть 1 содержит 13 заданий (А1–А10 и В1–В3) базового уровня по материалу курса математики. К каждому заданию А1–А10 приведены 4 варианта ответа, из которых только один верный. При выполнении этих заданий надо указать номер верного ответа. К заданиям В1–В3 надо дать краткий ответ.
Часть 2 содержит 10 более сложных заданий (В4–В11, С1, С2) по материалу курса математики. К заданиям В4–В11 надо дать краткий ответ, к заданиям С1 и С2 – записать решение.
Часть 3 содержит 3 самых сложных задания, два – алгебраических (С3, С5) и одно – геометрическое (С4). При их выполнении надо записать обоснованное решение.
Советуем для экономии времени пропускать задание, которое не удается выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у вас останется время.
Желаем успеха!
ЧАСТЬ 1
При выполнении заданий А1–А10 в бланке ответов №1 под номером выполняемого задания поставьте знак
"
×" в клеточке, номер которой соответствует номеру выбранного вами ответа.
101,4
 Упростите выражение . Упростите выражение .
0,7 10
1) 0,7 2) 2 3) 100,7
4) 102
| 1) 0,36
|
2) 3,4
|
3) 1,2
|
4) 0,012
|
 Вычислите: 3
0,064 27.⋅ Вычислите: 3
0,064 27.⋅
Вычислите: log 400 − log 25.
2 2
1) 8 2) 2 3) 3 4) 4
На одном из рисунков изображен график функции y
= log x
. Укажите
2
номер этого рисунка.
A5
Найдите производную функции h x
( ) = e
x
− 4x
2
.
1) h
′( )x
= e
x
− 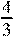 x
3 x
3
2) h
′( )x
= e
x
− 8x
3) h
′( )x
= e
x
− 2x
4) h
′( )x
= e
x
− 4x
Найдите множество значений функции y
= 3 cos x
.
1) (− ∞ + ∞; ) 2) [− 3; 3] 3) [−1; 1] 4) [0; 3]
 На рисунке показано изменение уровня воды водохранилища в течение 12 часов во время паводка. Как только уровень воды превысил отметку 10 метров, через сливные отверстия в плотине начали сбрасывать воду до того момента, пока её уровень понизился до отметки 10 метров. Определите, сколько часов длился сброс воды. На рисунке показано изменение уровня воды водохранилища в течение 12 часов во время паводка. Как только уровень воды превысил отметку 10 метров, через сливные отверстия в плотине начали сбрасывать воду до того момента, пока её уровень понизился до отметки 10 метров. Определите, сколько часов длился сброс воды.
1) 10 2) 2 3) 6 4) 4
6x
+18 Решите неравенство  ≤ 0. ≤ 0.
7x
1) [− 3; 0) ∪ (0; + ∞)
2) [− 3; 0)
3) [− 3; + ∞)
4) (− ∞; − 3] ∪ (0; + ∞)
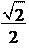 A9 A9
Решите уравнение cos x
−= 0.
1)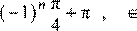  n n Z n n Z
2) n n Z n n Z
3)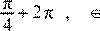 n n Z n n Z
4)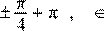 n n Z n n Z
Решите неравенство 46x
+11
≥16.
1) (− ∞; −1,5] 2) [−1,5; + ∞) 3) ⎢⎣⎡
− 5
3; + ∞) 4) (− ∞; − 5
3⎥⎦⎤
Ответом на задания В1–В11 должно быть некоторое целое число или число, записанное в виде десятичной дроби. Это число надо записать в бланк ответов №1 справа от номера выполняемого задания, начиная с первой клеточки. Каждую цифру, знак минус отрицательного числа и запятую в записи десятичной дроби пишите в отдельной клеточке в соответствии с приведенными в бланке образцами. Единицы измерений писать не нужно.
4 π
Найдите cosα, если sinα = , и 0 < α < .
5 2
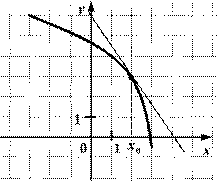 На рисунке изображён график функции у = f(х)
и касательная к нему в точке с абсциссой х
0
. Найдите значение производной в точке х
0
. На рисунке изображён график функции у = f(х)
и касательная к нему в точке с абсциссой х
0
. Найдите значение производной в точке х
0
.
 B3
Для оклейки стен ванной комнаты (см. 2 м рисунок) нужно приобрести керамическую плитку, причем плитка покупается с запасом в 10% от оклеиваемой площади. Ширина двери равна 0,75 м, высота – 2 м. Цена плитки 300 р. за 1 м2
. Определите стоимость плитки, если стены решено оклеить полностью, от пола до потолка. B3
Для оклейки стен ванной комнаты (см. 2 м рисунок) нужно приобрести керамическую плитку, причем плитка покупается с запасом в 10% от оклеиваемой площади. Ширина двери равна 0,75 м, высота – 2 м. Цена плитки 300 р. за 1 м2
. Определите стоимость плитки, если стены решено оклеить полностью, от пола до потолка.
ЧАСТЬ 2
x
 Решите уравнение 5x
+ 20⋅( 5) −125 = 0. Решите уравнение 5x
+ 20⋅( 5) −125 = 0.
 (Если уравнение имеет более одного корня, то в бланке ответов запишите их произведение.) (Если уравнение имеет более одного корня, то в бланке ответов запишите их произведение.)
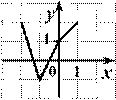
Функция у
= f
(x
) определена на промежутке (– 2; 7). На рисунке изображен график ее производной. Укажите точку минимума функции у
= f
(x
) на промежутке (− 2; 7).
 Вычислите значение выражения 6 6
+100 . Вычислите значение выражения 6 6
+100 .
Функция y
= f x
( ) определена на всей числовой
 прямой и является периодической с периодом 3. На рисунке изображен график этой функции при − 2 ≤ x
≤1. Найдите значение выражения f
( 1)− ⋅ f
(9) прямой и является периодической с периодом 3. На рисунке изображен график этой функции при − 2 ≤ x
≤1. Найдите значение выражения f
( 1)− ⋅ f
(9)
.
f
( 2)−
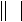 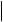 Найдите все значения a
, при каждом из которых уравнение x
+5− a
= 2 имеет ровно 3 корня. Найдите все значения a
, при каждом из которых уравнение x
+5− a
= 2 имеет ровно 3 корня.
(Если значений a
более одного, то в бланке ответов запишите их сумму.)
B9
Объемы ежегодной добычи нефти первой, второй и третьей скважинами
относятся как 6 : 7 : 10. Планируется уменьшить годовую добычу нефти из первой скважины на 10% и из второй – тоже на 10%. На сколько процентов нужно увеличить годовую добычу нефти из третьей скважины, чтобы суммарный объем добываемой за год нефти не изменился?
Концы отрезка MK
лежат на окружностях двух оснований цилиндра.
Угол между прямой MK
и плоскостью основания цилиндра равен 30°,
MK
= 8, площадь боковой поверхности цилиндра равна 40π. Найдите периметр осевого сечения цилиндра.
B11
Средняя линия прямоугольной трапеции равна 9, а радиус вписанной в нее окружности равен 4. Найдите большее основание трапеции.
Для записи ответов на задания С1 и С2 используйте бланк ответов №2. Запишите сначала номер выполняемого задания, а затем – решение.
Найдите наименьшее значение функции
2х
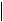 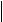 f x
( ) = f x
( ) =  при x
− 5,5 ≤ 2,5. при x
− 5,5 ≤ 2,5.
х
2 +16
Найдите все значения х,
при каждом из которых выражения
4 x
4 x
  sin 2x
и 2 sin 2
− 2 cos 2
принимают равные значения. tg x
tg x sin 2x
и 2 sin 2
− 2 cos 2
принимают равные значения. tg x
tg x
ЧАСТЬ 3
Для записи ответов на задания С3–С5 используйте бланк ответов №2. Запишите сначала номер выполняемого задания, а затем – обоснованное решение.
Найдите все значения x
>1, при каждом из которых наибольшее из двух чисел a
=log x
+ 2log 32 − 2 и b
= 41−log2
x
2
больше 5.
2 x
2
Около правильной пирамиды FABC
описана сфера, центр которой лежит в плоскости основания АВС
пирамиды. Точка М
лежит на ребре AB
так, что AM MB
: =1:3. Точка Т
лежит на прямой AF
и равноудалена от точек М
и B
. Объем пирамиды TВCM
равен  . Найдите радиус сферы, . Найдите радиус сферы,
описанной около пирамиды FABC
.
Найдите все значения параметра p
, при каждом из которых уравнение
x
(1,5p
− 7) 32⋅ 0,4x
+0,2
+ (29p
−154) 0,125⋅ −
3
+ 11p
− 41= 0 имеет ровно
10p
− p
2
− 24 различных корней.
ОТВЕТЫ К ЗАДАНИЯМ
ДЕМОНСТРАЦИОННОГО ВАРИАНТА ПО МАТЕМАТИКЕ
Ответы к заданиям с выбором ответа
| № задания
|
Ответ
|
№ задания
|
Ответ
|
| А1
|
3
|
А6
|
2
|
| А2
|
3
|
А7
|
4
|
| А3
|
4
|
А8
|
2
|
| А4
|
4
|
А9
|
2
|
| А5
|
2
|
А10
|
2
|
Ответы к заданиям с кратким ответом
| № задания
|
Ответ
|
| В1
|
0,6
|
| В2
|
-1,5
|
| В3
|
5940
|
| В4
|
2
|
| В5
|
2
|
| В6
|
13
|
| В7
|
– 0,5
|
| B8
|
7
|
| B9
|
13
|
| В10
|
28
|
| В11
|
12
|
Ответы к заданиям с развернутым ответом
| № задания
|
Ответ
|
| С1
|
0,2
|
| С2
|
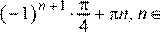 Z Z
|
| С3
|
1< x
<8, x
> 32
|
| 1
|
| С4
|
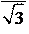
|
| С5
|
6
|
КРИТЕРИИ ПРОВЕРКИ И ОЦЕНКИ ВЫПОЛНЕНИЯ ЗАДАНИЙ С РАЗВЁРНУТЫМ ОТВЕТОМ
Найдите наименьшее значение функции
2х
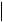  f x
( ) = f x
( ) =  при x
− 5,5 ≤ 2,5. при x
− 5,5 ≤ 2,5.
2
х
+16
Решение:
1)  x
−5,5 x
−5,5  ≤ 2,5 ⇔ − 2,5≤ x
−5,5≤ 2,5 ⇔ 3≤ x
≤ 8. ≤ 2,5 ⇔ − 2,5≤ x
−5,5≤ 2,5 ⇔ 3≤ x
≤ 8.
2(х
2
+16) − 2х х
⋅2 2
 ′( )x
= = 2⋅ 16 − х
. ′( )x
= = 2⋅ 16 − х
.
2) f
2 2 2 2
(х
+16) (х
+16)
f
′( )x
= 0 при x
= 4, при x
= − 4.
− 4∉[ 3;8].
f
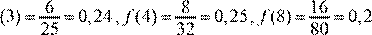 . .
Наименьшее значение функции y
= f x
( )на отрезке [3;8] равно 0,2.
Ответ:
0,2.
| Баллы
|
Критерии оценки выполнения задания С1
|
| 2
|
Приведена верная последовательность всех шагов решения: 1) определен промежуток, на котором требуется найти наименьшее значение функции;
2) найдено наименьшее значение функции.
Все преобразования и вычисления выполнены верно. Получен верный ответ.
|
| 1
|
Приведена верная последовательность всех шагов решения. Допущены описка и/или вычислительная ошибка в шаге 2), не влияющие на дальнейший ход решения.
В результате этой описки или ошибки может быть получен неверный ответ.
|
| 0
|
Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1 и 2 балла.
|
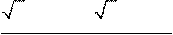  C2
Найдите все значения х,
при каждом из которых выражения sin 2x
2 sin 4 2
x
−
2 cos4 2
x
принимают равные значения. C2
Найдите все значения х,
при каждом из которых выражения sin 2x
2 sin 4 2
x
−
2 cos4 2
x
принимают равные значения.
и
tg x
tg x
Решение:
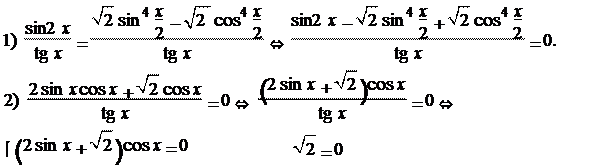 ⎧2 sin x
+ ⎧2 sin x
+
| ⎪⎪
⎨cos x
≠ 0
⎪
sin x
≠ 0
⎪⎩
|
⎪
⇔ ⎨cos x
≠ 0
⎪
sin x
≠ 0 ⎩
|
 , . , .
|
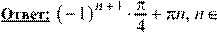 Z
. Z
.
| Баллы
|
Критерии оценки выполнения задания С2
|
| 2
|
Приведена верная последовательность всех шагов решения: 1) составлено уравнение по условию задачи; 2) найдены корни полученного уравнения.
Все преобразования и вычисления выполнены верно.
Получен верный ответ.
|
| 1
|
Приведена верная последовательность всех шагов решения.
Допущена вычислительная ошибка или описка в шаге 2), не влияющая на правильность дальнейшего хода решения. В результате этой ошибки или описки может быть получен неверный ответ.
|
| 0
|
Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1 и 2 балла.
|
C3
Найдите все значения x
>1, при каждом из которых наибольшее из двух
чисел a
=log x
+ 2log 32 − 2 и b
= −41 log2 2
x
больше 5.
2 x
2
Решение:
Так как x
>1, то log x
> 0.
2
1) a
>5⇔ log x
+2log 32 − 2 >5⇔  > ⇔ > ⇔
2 x
log x
2
⎡ log2
x
> 5
⇔ (log x
− 2) (⋅ log x
−5) > 0 ⇔ ⎢
2 2
⎢⎣log2 x
< 2.
2) 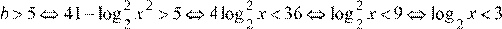 . .
3) Наибольшее из чисел a
и b
больше 5 тогда и только тогда, когда хотя бы одно из них больше 5, т.е. когда
⎡a
> 5 ⎡log2
x
> 5 ⎡x
> 32
⎢
⎣b
> 5 ⇔ ⎢
⎢⎣log2
x
< 3 ⇔ ⎣
⎢
x
< 8.
Ответ:
1< x
<8, x
> 32.
| Баллы
|
Критерии оценки выполнения задания С3
|
| 4
|
Приведено верное решение, содержащее в каком-либо порядке и виде следующие шаги:
1) решение первого неравенства;
2) решение второго неравенства;
3) составление совокупности указанных двух неравенств и ее решение.
Получен верный ответ.
|
| 3
|
Приведено логически верное решение, содержащее шаги 1), 2) и 3). Получен ответ.
Допустимы вычислительные ошибки, не влияющие на правильность дальнейшего хода решения. В результате этих ошибок возможен неверный ответ.
|
| 2
|
Верно выполнены шаги 1) и 2) решения, а шаг 3) либо отсутствует, либо не доведен до конца, либо выполнен неверно.
Ответ не получен или неверен.
|
| 1
|
Верно выполнен один из шагов 1) или 2) решения, а остальные шаги либо отсутствуют, либо не доведены до конца, либо выполнены неверно.
Ответ не получен или неверен.
|
| 0
|
Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1–4 балла.
|
C4
Около правильной пирамиды FABC
описана сфера, центр которой лежит в плоскости основания АВС
пирамиды. Точка М
лежит на ребре AB
так, что AM MB
: =1:3. Точка Т
лежит на прямой AF
и равноудалена от точек М
и B
. Объем пирамиды TВCM
равен 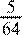 . Найдите радиус сферы, . Найдите радиус сферы,
описанной около пирамиды FABC
.
Решение:
1)  Пусть O – центр сферы радиуса R, описанной около пирамиды FABC. Так как OA = OB = OC = OF = R , а О ∈ АВС, то точка О является также центром окружности радиуса R, описанной около треугольника АВС. Треугольник АВС – правильный, следовательно, О – точка пересечения медиан треугольника АВС, Пусть O – центр сферы радиуса R, описанной около пирамиды FABC. Так как OA = OB = OC = OF = R , а О ∈ АВС, то точка О является также центром окружности радиуса R, описанной около треугольника АВС. Треугольник АВС – правильный, следовательно, О – точка пересечения медиан треугольника АВС,
 AB R 3=. A M N P B AB R 3=. A M N P B
2) FABC – правильная пирамида, поэтому FO – высота пирамиды и AFO ⊥ ABC. По условию T∈AF и TM TB= . Опустим из точки T перпендикуляр TН на прямую АO. Так как AFO ⊥ ABC, то TH ⊥ ABC, и следовательно, ТН – высота пирамиды TВCM, а отрезки НМ и HB – проекции равных наклонных TМ и TB. Значит, HM HB= , и поэтому треугольник ВНМ – равнобедренный, а его высота НР является медианой, то есть PM PB= .
3) Объем V пирамиды TВCM, равный 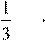 TH SBCM
, выразим через R. Из TH SBCM
, выразим через R. Из
 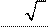 1 R 3 3R 3 1 R 3 3R 3
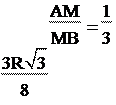 условия имеем AM = условия имеем AM =  AB = , MB = , AB = , MB = ,
4 4 4
MP = . Отсюда AP = 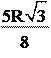 . В прямоугольном треугольнике . В прямоугольном треугольнике
 АРН угол А равен 30D
, следовательно, AH = AP
= 5R
. Так как cos30D
4 АРН угол А равен 30D
, следовательно, AH = AP
= 5R
. Так как cos30D
4
OA = OF, то прямоугольный треугольник AOF – равнобедренный, поэтому в прямоугольном треугольнике АТН угол А равен 45D
, следовательно, AH TH= . Медиана CN правильного треугольника АВС является его высотой. Поэтому CN – высота треугольника ВСМ.
Следовательно, площадь треугольника ВСМ можно найти по формуле
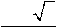 3 3R 9R2
3 3 3R 9R2
3
SBCM
= 0,5CN B⋅ M. Имеем CN =  CO = CO =  и SBCM
= . Отсюда и SBCM
= . Отсюда
2 2 16
 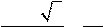 1 5R 9R2
3 15R3
3 15R3
3 5 1 5R 9R2
3 15R3
3 15R3
3 5
V = ⋅ ⋅ = . По условию = ,
3 4 16 64 64 64
3
1 1
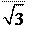 откуда R = и R=. откуда R = и R=.
 3 3 3 3
Ответ:
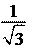 . .
| Баллы
|
Критерии оценки выполнения задания С4
|
| 4
|
Приведена верная последовательность шагов решения:
1) установлено, что центром сферы, описанной около пирамиды FABC, является точка пересечения медиан треугольника АBС;
2) установлено положение основания Н высоты TH пирамиды TBCM;
3) площадь основания, высота и объем пирамиды TBCM выражены через радиус R сферы, описанной около пирамиды FABC, вычислена искомая величина R.
Верно обоснованы ключевые моменты решения:
а) центр сферы, описанной около пирамиды FABC, – точка пересечения медиан основания пирамиды; б) основание H высоты TH пирамиды TBCM лежит на прямой АО, содержащей медиану треугольника АBС. Все преобразования и вычисления выполнены верно. Получен верный ответ.
|
| 3
|
Приведены все шаги решения 1) – 3).
Приведены утверждения, составляющие ключевые моменты а) и б) решения. Допустимы отсутствие обоснований ключевых моментов решения или неточности в обоснованиях[1]
, но не грубые ошибки.
Допустимы одна описка и/или негрубая ошибка в вычислениях, не влияющие на правильность хода решения. В результате этой описки и/или ошибки возможен неверный ответ.
|
| 2
|
Приведены шаги решения 1) – 3).
Утверждения, составляющие ключевые моменты а) и б) решения, либо оба отсутствуют, либо приведено только одно из них. Но сами ключевые моменты использованы в решении. Приведенные в решении обоснования не содержат грубых ошибок.
Допустимы описки и/или негрубые ошибки в вычислениях, не влияющие на правильность хода решения. В результате этого возможен неверный ответ.
|
| 1
|
Ход решения правильный, но решение не завершено: указано положение центра описанной сферы (описано словесно либо отражено на чертеже). Найдены некоторые числовые
|
| характеристики пирамид, например, длина отрезка АР выражена через радиус R сферы, описанной около пирамиды FABC.
Приведенные в решении обоснования и вычисления не содержат грубых ошибок. Допустимы негрубые ошибки в преобразованиях и вычислениях, не влияющие на правильность хода решения.
|
| 0
|
Все случаи решения, которые не соответствуют вышеуказанным критериям выставления 1 – 4 баллов.
|
C5
Найдите все значения параметра p
, при каждом из которых уравнение
x
(1,5p
− 7) 32⋅ 0,4x
+0,2
+ (29p
−154) 0,125⋅ −
3
+ 11p
− 41= 0 имеет ровно
10p
− p
2
− 24 различных корней.
Решение:
−x −x
1) Так как 320,4x
+0,2 = (2 )5 0,4x
+0,2 = 22x
+1 = 2 4⋅ x
, 0,125 3 = (2−3) 3 = 2x
, то (3p
−14)4x
+ (29p
−154)2x
+11p
− 41= 0.
Пусть t
= 2x
> 0. Тогда получаем квадратное уравнение относительно t
с параметром p
:
(3p
−14)t
2
+ (29p
−154)t
+11p
− 41= 0. (*)
Значит, число n
различных корней исходного уравнения не больше 2.
2) Если n
= 2, то по условию 10p
− p
2
− 24 = 2, p
2
−10p
+ 26 = 0, что невозможно, т.к. D
= − 4 < 0. Остаются случаи n
=1 и n
= 0.
Если n
=1, то 10p
− p
2
− 24 =1, p
2
−10p
+ 25 = 0, p
= 5. Тогда уравнение (*) примет вид t
2
−9t
+14 = 0, t
= 2, t
= 7 . Так как t
= 2x
, то
1 2
x
=1, x
= log 7. Поэтому n
= 2. Противоречие с равенством n
=1.
1 2 2
3) Если n
= 0, то 10p
− p
2
− 24 = 0, p
2
−10p
+ 24 = 0, p
= 4, p
= 6.
1 2
Пусть p
= 4. Тогда уравнение (*) примет вид − 2t
2
−38t
+ 3= 0. Ветви параболы направлены вниз, ось Oy
она пересекает выше точки (0; 0). Поэтому уравнение (*) имеет ровно один положительный корень t
и
0
исходное уравнение имеет ровно один корень x
= log t
. Значит, n
=1.
2 0
Противоречие с равенством n
= 0.
Пусть p
= 6. Тогда уравнение (*) примет вид
4t
2
+ 20t
+ 25 = 0, t
= − 2,5. Так как t
= 2x
> 0, то исходное уравнение не имеет корней. Значит, p
= 6 удовлетворяет условию задачи.
Ответ:
6.
ЗАМЕЧАНИЯ.
А) В шаге 2) не обязательно явно указывать 2 корня исходного уравнения. Допустимо использование только положительности корней уравнения (*).
Б) В шагах 2) – 3) можно не объяснять, как найдены корни квадратного уравнения.
В) В шаге 3) можно явно решить квадратное уравнение относительно t
и указать его положительный корень.
| Баллы
|
Критерии оценки выполнения задания С5
|
| 4
|
Приведена верная последовательность всех шагов решения: 1) тождественные преобразования показательных выражений и
оценка n
≤ 2 числа корней исходного уравнения;
2) разбор случаев n
= 2 и n
= 1;
3) разбор случая n
= 0, проверка того, что р
= 6 удовлетворяет условию.
Обоснованы все моменты решения:
а) в шаге 2) явно указаны два корня исходного уравнения или же их существование объяснено ссылкой на неравенство t
> 0;
б) в шаге 2) разбор случаев n
= 2 и n
= 1 обоснован свойствами квадратичной функции и/или явным указанием её нулей; в) в шаге 3) имеется ссылка на условие t
> 0.
Все преобразования и вычисления верны. Получен верный ответ.
|
| 3
|
Приведена верная последовательность всех шагов решения. В шаге 3) допустимо отсутствие обоснования в). Обоснованы ключевые моменты а) и б).
Допустимы 1 описка и/или негрубая вычислительная ошибка в шаге 3), не влияющие на правильность дальнейшего хода решения. В результате может быть получен неверный ответ.
|
| 2
|
Приведена в целом верная, но, возможно, неполная последовательность шагов решения. Верно выполнен шаг 1). В шаге 2) верно исследован только один из случаев n
= 2 или n
= 1. При их рассмотрении обоснован хотя бы один из ключевых моментов а), б).
Допустимо, что решение не завершено.
|
| 1
|
Общая идея, ход решения верны. Верно выполнен шаг 1): исходное уравнение сведено к квадратному относительно новой переменной. Получена оценка n
≤ 2 числа корней исходного уравнения.
Допустимо, что решение не завершено.
|
| 0
|
Все случаи решения, которые не соответствуют указанным выше критериям выставления оценок в 1, 2, 3, 4 балла.
|
[1]
Неточностью в обоснованиях является замена свойства на определение или на признак или наоборот, а также неверные названия теорем или формул.
|