МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ НЕГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ КОЛЛЕДЖ УПРАВЛЕНИЯ ИНФОРМАТИКИ И СЕРВИСА (ИМСИТ)
Курсовая работа
по дисциплине «МАТЕМАТИЧЕСКИЕ МЕТОДЫ»
Вариант 3.
Выполнил:
студент группы ПО-3-3
специальности 230105
«Программное обеспечение
вычислительной техники и
автоматизированных систем»
Горбунов Дмитрий Валерьевич
Проверил:
Шихина В. А.
Краснодар, 2006
СОДЕРЖАНИЕ
Введение … … … … … … … … … … … … … … … … … … … … … … … … … . 2 Графический метод решения задач … … … … … … … … … … … … … … … … 3
Теория двойственности … … … … … … … … … … … … … … … … … … … ... 6
Симплексный метод … … … … … … … … … … … … … … … … … … … … … .. 10
Транспортная задача … … … … … … … … … … … … … … … … … … … … … . 13
Список использованной литературы … … … … … … … … … … … … … … … … 24
ВВЕДЕНИЕ
Исследование операций —
научная дисциплина, занимающаяся разработкой и практическим применением методов наиболее эффективного управления различными организационными системами.
Управление любой системой реализуется как процесс, подчиняющийся определенным закономерностям. Их знание помогает определить условия, необходимые и достаточные для осуществления данного процесса. Для этого все параметры, характеризующие процесс и внешние условия, должны быть количественно определены, измерены. Следовательно, цель исследования операций — количественное обоснование принимаемых решений
по организации управления.
При решении конкретной задачи управления применение методов исследования операций предполагает:
• построение экономических и математических моделей для
задач принятия решения в сложных ситуациях или в условиях
неопределенности;
• изучение взаимосвязей, определяющих впоследствии принятие решений, и установление критериев эффективности,
позволяющих оценивать преимущество того или иного варианта действия.
Примерами задач исследования операций, отражающих его специфику, могут служить следующие задачи.
Графический метод решения задач линейного
программирования с двумя переменными
.
Графический метод используется для решения задач с двумя переменными следующего вида:
Z(X) = c1
x1
+ c2
x2
→ max (min)
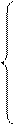 a11
x1
+ a12
x2
≤ (≥) b1
, a11
x1
+ a12
x2
≤ (≥) b1
,
a21
x1
+ a22
x2
≤ (≥) b2
,
……………………………..
am1
x1
+ am2
x2
≤ (≥) bm
x1
≥0, x2
≥0
Данный метод основывается на возможности графического изображения области допустимых решений задачи и нахождения среди них оптимального решения.
Область допустимых решений задачи строится как пересечение областей решений каждого из заданных ограничений.
Областью решений
линейного неравенства ai
1
x1
+ ai
2
x2
≤bi
является одна из двух полуплоскостей, на которые прямая ai
1
x1
+ ai
2
x2
= 0, соответствующая данному неравенству, делит всю координатную плоскость. Для того, чтобы определить, какая из полуплоскостей является областью решений, достаточно координаты какой-либо точки, не лежащей на прямой, подставить в неравенство: если оно удовлетворяется, то областью решений является полуплоскость, содержащая эту точку, если не удовлетворяется – то полуплоскость, не содержащая данную точку .
Для нахождения среди допустимых решений оптимального используют линии уровня и опорные прямые. Линией уровня
называется прямая, на которой целевая функция задачи принимает постоянное значение. Уравнение линии уровня имеет вид c1
x1
+ c2
x2
= L , где L = const. Все линии уровня параллельны между собой. Опорной прямой
называется линия уровня, которая имеет хотя бы одну общую точку с областью допустимых решений и по отношению к которой эта область находиться в одной из полуплоскостей. Важное свойство линии уровня: при параллельном смещении линии в одну сторону уровень возрастает, а в другую сторону – убывает.
I
Задание:
Решить графическим методом задачу с двумя переменными.
Z(x)=2х1
+3х2
→ max
-6х1
+х2
≥3
-5х1
+9х2
≤ 45
х1
-3х2
≤ 3
х1
≥ 0 , х2
≥ 0
Найдем точки пересечения прямых с осями координат:
I. -6х1
+х2
=3
1)х1
=0 2)х2
=0
х2
=3 х1
= -1/2
II. -5х1
+9х2
=45
1)х1
=0 2)х2
=0
х2
=5 х1
= -9
III. х1
-3х2
=3
1)х1
=0 2)х2
=0
х2
= -1 х1
=3
Построим область решения данной системы:
Найдем вектор направленности целевой функции
Z(х)=2х1
+3х2
=0
1)х1
=0 2)х1
=3
х2
=0 х2
= -2
Z(х)=2х1
+3х2
=6
1)х1
=0 2)х2
=0
х2
=2 х1
=3
Ответ: Целевая функция принимает максимальное
значение в точке(0;0), при х1
=0 и х2
=0.
Теория двойственности.
Любой задаче линейного программирования, называемой исходной,
можно поставить в соответствие другую задачу, которая называется двойственной.
Обе эти задачи образуют пару двойственных задач. Каждая из задач является двойственной к другой задаче.
Алгоритм составления двойственной задачи:
1) Привести все неравенства ограничений исходной задачи к единому смыслу: если в исходной задаче ищется максимум линейной функции, то все неравенства системы ограничений привести к виду «≤», а если минимум – к виду «≥». Для этого неравенства, в которых данное требование не выполняется, умножить на -1.
2) Составить расширенную матрицу системы – А, в которую включить матрицу коэффициентов при переменных А, столбец свободных членов системы ограничений и строку коэффициентов при переменных в линейной функции.
3) Найти матрицу А` транспонированную к матрице А
4) Сформулировать двойственную задачу на основании полученной матрицы А` и условия неотрицательности переменных.
Основная теорема двойственности:
Если одна из взаимно двойственных задач имеет оптимальное решение, то его имеет и другая, причем оптимальные значения их целевых функций равны. Если линейная функция одной задачи неограниченна, то условия другой задачи противоречивы.
Вторая теорема двойственности
: Компоненты оптимального решения двойственной задачи равны абсолютным значениям коэффициентов при соответствующих переменных линейной функции исходной задачи, выраженной через неосновные переменные ее оптимального решения.
II
Задание:
Решить графическим методом задачу с двумя переменными.
Z(х)=4х1
+13х2
+3х3
+6х4
→ min
При ограничениях:
-5х1
+3х2
-х3
+2х4
+х5
= -1
9х1
-4х2
+2х3
-3х4
+х6
= 6
Учитывая условия неотрицательности:
хj
≥ 0 , j=1,2,3,4.
Для решения данной задачи необходимо перевести систему ограничений в стандартный вид путём введения дополнительных переменных:
-5х1
+3х2
-х3
+2х4
+х5
≥ -1
9х1
-4х2
+2х3
-3х4
+х6
≥ 6
Составим расширенную матрицу системы уравнений
-5 3 -1 2 1 0 -1
А= 9 -4 2 -3 0 1 6
4 13 3 6 0 0 Z
Найдем транспонированную матрицу системы уравнений
-5 9 4
3 -4 13
-1 2 3
А′ = 2 -3 6
1 0 0
0 1 0
-1 6 F
Составим новую систему ограничений
F(y)= -у1
+6у2
→ max
-5у1
+9у2
≤ 4
3у1
+4у2
≤ 13
-у1
+2у2
≤ 3
2у1
-3у2
≤ 6
у1
≤ 0
у2
≤ 0
у1
≥ 0 ; у2
≥ 0
Найдем точки пересечения прямых с осями координат:
I. -5у1
+9у2
≤ 4
1)у1
=0 2)у2
=0
у2
=4/9 у1
= -4/5
II. 3у1
+4у2
≤ 13
1)у1
=0 2)у2
=0
у2
= -13/4 у1
=13/3
III. -у1
+2у2
≤ 3
1)у1
=0 2)у2
=0
у2
=3/2 у1
= -3
IV. 2у1
-3у2
≤ 6
1)у1
=0 2)у2
=0
у2
= -2 у1
=3
Построим область решений системы неравенств:
FA
=9 - max
FB
=4/9*6=8/3=2*2/3 - min
Ответ: по теореме двойственности Fmax
= Zmin
= 9
Данный метод состоит в целенаправленном переборе опорных решений задачи линейного программирования. Он позволяет за конечное число шагов расчета либо найти оптимальное решение, либо установить его отсутствие.
Для реализации симплексного метода – последовательного улучшения решения – необходимо освоить три основных элемента
:
· способ определения какого – либо первоначального допустимого базисного решения задачи;
· правило перехода к лучшему (точнее, не худшему) решению;
· критерий проверки оптимальности найденного решения.
III
Задание:
Решить задачу симплексным методом.
Z(x)=x1
-x2
+x3
→ max
При ограничениях:
4x1
+2x2
+x3
≥ 6
-x1
+x2
+x3
= 1
x1
-x2
+4x3
≤ 24
Учитывая условия неотрицательности:
xj
≥ 0 , j=1,2,3
Для нахождения первоначального базисного решения разобьем переменные на две группы – основные и свободные. В качестве основных переменных на первом шаге следует выбирать такие m переменные, каждая из которых входит только в одно из m уравнений системы, в которые не входит не одна из этих переменных. Свободные переменные удовлетворяют этому правилу.
I шаг:
Основные переменные: х2
, х4
, х5
Свободные переменные: х1
, х3
С помощью дополнительных неотрицательных переменных перейдём к системе уравнений:
x2
=1+x1
-x3
x4
=-4+6x1
-3x3
x5
=25+3x3
Получим первое базисное решение, которое является недопустимым т.к. присутствует отрицательный компонент
X1=(0,1,0,-4,25) – недопустимое базисное решение.
х3
=min{1,∞,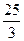 }=1 }=1
II Шаг
Основные переменные: х1
, х2
, х5
Свободные переменные: х3
, х4
Выразимновыеосновныепеременныечерезнеосновные:
х1
=2/3+х3
/2+х4
/6
x2
=5/3+x3
/2+x4
/6
x5
=25+x3
Получим второе базисное решение, которое является допустимым т.к. отрицательных компонентов нет.
X2=(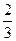 , ,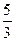 ,0,0,25) – допустимое базисное решение. ,0,0,25) – допустимое базисное решение.
Выражаем линейную функцию через неосновные переменные:
Z(x)=2/3+x3
/2+x4
/6-5/3-x3
/2-x4
/6+25+x3
=24+x3
=24.
Так как в выражении линейной функции через неосновные переменные отсутствуют отрицательные коэффициенты при неосновных переменных, то решение оптимально.
Транспортная задача линейного программирования
Под названием транспортная задача объединяется широкий круг задач с единой математической моделью. Классическая транспортная задача – это задача о наиболее экономном плане перевозок однородного продукта или взаимозаменяемых продуктов из пунктов производства в пункты потребления.
Исходные данные транспортной задачи записываются в таблице вида:
| b1
|
b2
|
… |
bn
|
| a1
|
c11
|
c12
|
… |
c1
n
|
| a2
|
c21
|
c22
|
… |
c2
n
|
| … |
… |
… |
… |
… |
| am
|
cm
1
|
cm
2
|
… |
cmn
|
Где ai
– объемы поставок, bj
– объемы потребления, сmn
– стоимости перевозок.
Переменными транспортной задачи являются xij
– объемы перевозок от каждого i-го поставщика каждому j-му потребителю. В рассмотренной задаче предполагается, что суммарные запасы поставщиков равны суммарным запасам потребителей, такая задача называется задачей с правильным балансом
, а ее модель – закрытой
. Если же равенство не выполняется, то задача называется задачей с неправильным балансом
, а ее модель – открытой
. Для того, чтобы транспортная задача имела решение, необходимо и достаточно, чтобы суммарные запасы поставщиков равнялись суммарным запросам потребителей, т. е. задача должна бать с правильным балансом.
Метод северо-западного угла
Согласно данному методу запасы очередного поставщика используются для обеспечения запросов очередных потребителей до тех пор, пока не будут исчерпаны полностью, после чего используются запасы следующего по номеру поставщика. Во избежание ошибок после построения начального опорного решения необходимо проверить, что число занятых клеток равно m + n -1.
Метод минимальной стоимости
Этот метод состоит из ряда однотипных шагов, на каждом из которых заполняется только одна клетка таблицы, соответствующая минимальной стоимости, и исключается из рассмотрения только одна строка (поставщик) или один столбец (потребитель).
Алгоритм решения транспортных задач методом потенциалов:
· Проверить выполнение необходимого и достаточного условия разрешимости задачи. Если задача имеет неправильный баланс, то вводиться фиктивный поставщик или потребитель с недостающими запасами или запросами и нулевыми стоимостями перевозок;
· Построить начальное опорное решение, проверить правильность его построения по количеству занятых клеток (их должно быть m + n - 1);
· Построить систему потенциалов, соответствующих опорному решению. Для этого решают систему уравнений ui
+ vj
= cij
при xij
>=0, которая имеет бесконечное множество решений. Для нахождения частного решения системы одному из потенциалов задают произвольно некоторое значение. Остальные потенциалы считаются по формулам ui
= cij
- vj
и vj
= cij
- ui
.
· Проверить выполнение условия оптимальности для свободных клеток таблицы. Для этого вычисляют оценки для всех свободных клеток Dij
= ui
+ vj
- cij
, если Dij
>=0 , то полученное решение считается оптимальным, если нет то подлежит улучшению;
· Перейти к новому опорному решению, на котором значение целевой функции будет меньше. Для этого строят циклы.
IV
Задание:
I
способ: распределение поставок
методом минимальной стоимости.
Распределим поставки методом наименьшей стоимости, посчитаем потенциалы и значение целевой функции.

|
1 |
2 |
1 |
3 |
0 |
-2 |
| 200 |
400 |
100 |
200 |
100 |
300 |
| 0 |
200 |
1 |
1 |
12 |
2 |
5 |
0 |
 200 200 |
[-1] |
| 1 |
100 |
2 |
3 |
8 |
4 |
7 |
0 |
| =0= |
100 |
| 3 |
200 |
3 |
5 |
4 |
6 |
9 |
0 |
| [-1] |
=0= |
200 |
| 2 |
400 |
4 |
4 |
3 |
8 |
2 |
0 |
| 100 |
=0= |
300 |
| 1 |
400 |
5 |
3 |
7 |
10 |
1 |
0 |
| 300 |
100 |
F=3000

|
-1 |
1 |
0 |
2 |
-1 |
-3 |
| 200 |
400 |
100 |
200 |
100 |
300 |
| 0 |
200 |
1 |
1 |
12 |
2 |
5 |
0 |
| 200 |
| 2 |
100 |
2 |
3 |
8 |
4 |
7 |
0 |
| 100 |
=0= |
| 4 |
200 |
3 |
5 |
4 |
6 |
9 |
0 |
| 200 |
=0= |
| 3 |
400 |
4 |
4 |
3 |
8 |
2 |
0 |
| 100 |
=0= |
300 |
| 2 |
400 |
5 |
3 |
7 |
10 |
1 |
0 |
| 300 |
100 |
F=2600
Клеток с отрицательными потенциалами нет, значит, мы нашли оптимальный план распределения поставок. Fmin = 2600
II
способ: распределение поставок
методом северо-западного угла
F=4800
Распределим поставки методом северо-западного угла, посчитаем потенциалы и значение целевой функции.

|
-1 |
1 |
0 |
2 |
-1 |
-2 |
| 200 |
400 |
100 |
200 |
100 |
300 |
| 0 |
200 |
1 |
7 |
12 |
2 |
5 |
0 |
| 200 |
| 2 |
100 |
2 |
3 |
8 |
4 |
7 |
0 |
| 100 |
=0= |
| 4 |
200 |
3 |
5 |
4 |
6 |
9 |
0 |
| 200 |
=0= |
| 3 |
400 |
4 |
 4 4 |
3 |
8 |
2 |
0 |
| 300 |
100 |
=0= |
[-1] |
| 2 |
400 |
5 |
3 |
7 |
10 |
1 |
0 |
| 100 |
300 |
F=2900

|
-1 |
1 |
0 |
2 |
-1 |
-3 |
| 200 |
400 |
100 |
200 |
100 |
300 |
| 0 |
200 |
1 |
7 |
12 |
2 |
5 |
0 |
| 200 |
| 2 |
100 |
2 |
3 |
8 |
4 |
7 |
0 |
| 100 |
=0= |
| 4 |
200 |
3 |
5 |
4 |
6 |
9 |
0 |
| 200 |
=0= |
| 3 |
400 |
4 |
4 |
3 |
8 |
2 |
0 |
| 100 |
300 |
| 2 |
400 |
5 |
3 |
7 |
10 |
1 |
0 |
| 300 |
100 |
F=2600
Клеток с отрицательными потенциалами нет, значит мы нашли оптимальный план распределения поставок. Fmin =2600
Транспортная задача с ограничениями на пропускную способность
Если требуется при решении транспортной задачи ограничить перевозки от поставщика с номером l к потребителю с номером k. Возможны ограничения двух типов xlk
>= a и xlk
=< b, где a и b – постоянные величины.
1. Если xlk
>= a, то необходимо, прежде чем решать задачу, сократить запасы l-го поставщика и запросы k-го потребителя на величину а (зарезервировать перевозку xlk
= a). В полученном оптимальном решении следует увеличить объем перевозки xlk
на величину а.
2. Если xlk
=< b, то необходимо вместо k-го потребителя с запросами bk
ввести двух других потребителей. Один из них с номером k должен иметь запасы bk
` = b, а другой с номером n+1 – запросы bn
+1
= bk
– b. Стоимости перевозок для этих потребителей остаются прежними, за исключением cl
(
n
+1)
, которая принимается равной сколь угодно большому числу М. После получения оптимального решения величины грузов, перевозимых к (n+1)-му потребителю, прибавляются к величинам перевозок k-го потребителя. Так как cl
(
n
+1)
= М, то в оптимальном решении клетка с номером (l, n+1) останется пустой (xl
(
n
+1)
= 0) и объем перевозки xlk
не превзойдет b.
V
Задание:
I
способ: распределение поставок
методом минимальной стоимости
x21
=< 500 и x44
>= 1000
| 1000 |
1000 |
2000 |
2000 |
| 500 |
5 |
6 |
3 |
8 |
| 1000 |
1 |
1 |
2 |
3 |
| 1500 |
2 |
5 |
4 |
4 |
| 2000 |
6 |
3 |
5 |
9 |
Вместо 1 потребителя вводим двух других. Сокращаем запасы 4 поставщика и запросы 4 потребителя на 1000.
| 500 |
1000 |
2000 |
1000 |
500 |
| 500 |
5 |
6 |
3 |
8 |
5 |
| 1000 |
1 |
1 |
2 |
3 |
M |
| 1500 |
2 |
5 |
4 |
4 |
2 |
| 1000 |
6 |
3 |
5 |
9 |
6 |
Решаем транспортную задачу как обычно.
Данная задача с неправильным балансом, добавляем фиктивного потребителя с потребностями равными 1000, и стоимостями перевозок равными 0. Распределим поставки методом наименьшей стоимости, посчитаем потенциалы и значение целевой функции.
| V1
= 1 |
V2
= 1 |
V3
= 3 |
V4
= 3 |
V5
= 1 |
| 500 |
1000 |
2000 |
1000 |
500 |
| U1
= 0 |
500 |
5 |
6 |
500
3 |
8 |
5 |
| U2
= 0 |
1000 |
500
1 |
 500
1 500
1 |
-1
2 |
0
3 |
M |
| U3
= 1 |
1500 |
2 |
5 |
1000
4 |
4 |
500
2 |
| U4
= 2 |
1000 |
6 |
500
3 |
500
5 |
9 |
6 |
| U5
= -3 |
1000 |
0 |
0 |
0 |
1000
0 |
0 |
F=11500
| V1
= 1 |
V2
= 1 |
V3
= 2 |
V4
= 2 |
V5
= 0 |
| 500 |
1000 |
2000 |
1000 |
500 |
| U1
= 1 |
500 |
5 |
6 |
500
3 |
8 |
5 |
| U2
= 0 |
1000 |
 500
1 500
1 |
0
1 |
500
2 |
0
3 |
M |
| U3
= 2 |
1500 |
-1
2 |
5 |
1000
4 |
4 |
500
2 |
| U4
= 2 |
1000 |
6 |
1000
3 |
5 |
9 |
6 |
| U5
= -2 |
1000 |
0 |
0 |
0
0 |
1000
0 |
0 |
F=11000
| V1
= 1 |
V2
= 1 |
V3
= 2 |
V4
= 2 |
V5
= 0 |
| 500 |
1000 |
2000 |
1000 |
500 |
| U1
= 1 |
500 |
5 |
6 |
500
3 |
8 |
5 |
| U2
= 0 |
1000 |
1 |
0
1 |
1000
2 |
0
3 |
M |
| U3
= 2 |
1500 |
500
2 |
5 |
500
4 |
4 |
500
2 |
| U4
= 2 |
1000 |
6 |
1000
3 |
5 |
9 |
6 |
| U5
= -2 |
1000 |
0 |
0 |
0
0 |
1000
0 |
0 |
Клеток с отрицательными потенциалами нет, значит мы нашли оптимальный план распределения поставок. Fmin = 10 500
Запишем оптимальное решение исходной задачи. Для этого увеличим объем перевозки x44
на 1000 единиц и объединим объемы перевозок 1 и 5 потребителя. Получим
| 1000 |
1000 |
2000 |
2000 |
| 500 |
5 |
6 |
500
3 |
8 |
| 1000 |
1 |
1 |
1000
2 |
3 |
| 1500 |
1000
2 |
5 |
500
4 |
4 |
| 2000 |
6 |
1000
3 |
5 |
1000
9 |
| 1000 |
0 |
0 |
0 |
1000
0 |
F = 19 500
II
способ: распределение поставок
методом северо-западного угла
Распределим поставки методом северо-западного угла, посчитаем потенциалы и значение целевой функции.
| V1
= 7 |
V2
= 7 |
V3
= 5 |
V4
= 9 |
V5
= 9 |
| 500 |
1000 |
2000 |
1000 |
500 |
| U1
= -2 |
500 |
 500
5 500
5 |
6 |
3 |
8 |
5 |
| U2
= -6 |
1000 |
0
1 |
1000
1 |
2 |
0
3 |
M |
| U3
= -1 |
1500 |
-4
2 |
-1
5 |
1500
4 |
-4
4 |
-6
2 |
| U4
= 0 |
1000 |
-1
6 |
-4
3 |
500
5 |
500
9 |
-3
6 |
| U5
= -9 |
1000 |
0 |
0 |
0 |
500
0 |
500
0 |
F = 16 500
| V1
= 2 |
V2
= 2 |
V3
= 4 |
V4
= 8 |
V5
= 8 |
| 500 |
1000 |
2000 |
1000 |
500 |
| U1
= -1 |
500 |
5 |
6 |
500
3 |
8 |
5 |
| U2
= -1 |
1000 |
0
1 |
1000
1 |
-1
2 |
-5
3 |
M |
| U3
= 0 |
1500 |
500
2 |
5 |
  1000
4 1000
4 |
-4
4 |
 -6
2 -6
2 |
| U4
= 1 |
1000 |
6 |
3 |
 500
5 500
5 |
 500
9 500
9 |
-3
6 |
| U5
= -8 |
1000 |
0 |
0 |
0 |
 500
0 500
0 |
500
0 |
F = 14 500
| V1
= 2 |
V2
= 2 |
V3
= 4 |
V4
= 4 |
V5
= 2 |
| 500 |
1000 |
2000 |
1000 |
500 |
| U1
= -1 |
500 |
5 |
6 |
500
3 |
8 |
5 |
| U2
= -1 |
1000 |
0
1 |
 1000
1 1000
1 |
-1
2 |
3 |
M |
| U3
= 0 |
1500 |
500
2 |
5 |
500
4 |
4 |
500
2 |
| U4
= 1 |
1000 |
6 |
3 |
1000
5 |
9 |
6 |
| U5
= -4 |
1000 |
0 |
0 |
0
0 |
500
0 |
0 |
F = 11 500
| V1
= 1 |
V2
= 1 |
V3
= 2 |
V4
= 2 |
V5
= 0 |
| 500 |
1000 |
2000 |
1000 |
500 |
| U1
= 1 |
500 |
5 |
6 |
500
3 |
8 |
5 |
| U2
= 0 |
1000 |
1 |
0
1 |
1000
2 |
0
3 |
M |
| U3
= 2 |
1500 |
500
2 |
5 |
500
4 |
4 |
500
2 |
| U4
= 2 |
1000 |
6 |
1000
3 |
5 |
9 |
6 |
| U5
= -2 |
1000 |
0 |
0 |
0
0 |
1000
0 |
0 |
Клеток с отрицательными потенциалами нет, значит мы нашли оптимальный план распределения поставок. Fmin = 10 500. Запишем оптимальное решение исходной задачи. Для этого увеличим объем перевозки x44
на 1000 единиц и объединим объемы перевозок 1 и 5 потребителя. Получим
| 1000 |
1000 |
2000 |
2000 |
| 500 |
5 |
6 |
500
3 |
8 |
| 1000 |
1 |
1 |
1000
2 |
3 |
| 1500 |
1000
2 |
5 |
500
4 |
4 |
| 2000 |
6 |
1000
3 |
5 |
1000
9 |
| 1000 |
0 |
0 |
0 |
1000
0 |
F=19 500
Вывод:
функция принимает минимальное значение 19 500.
Список использованной литературы
1. Исследование операций в экономике: Учеб. пособие для вузов. Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман; под редакцией проф. Н.Ш. Кремера. – М.: ЮНИТИ, 2004.
2. Сборник задач по высшей математике для экономистов: Учебное пособие. Под ред. В.И. Ермакова. – М.: ИНФРА – М, 2004.
3. Высшая математика для экономистов: теория, примеры, задачи. Клименко Ю.И..- М.: Экзамен, 2005.
4. Справочное пособие по высшей математике. Боярчук А.К., Головач Г.П.
|