Курсовая работа: Алгоритмынахождениякратчайшихпутейвграфе

Государственное образовательное учреждение

Высшее профессиональное образование

Донской государственный технический университет кафедра ПОВТ и АС

Отчет по курсовой работе по курсу «Алгоритмы, построение и анализ»

на темы«Алгоритмы нахождения кратчайших путей в графе.»

Выполнил ст. гр. УСУ‐21

Герусов К.А.

Руководитель работы:

Горлова М.Ю.

Медведева Т.А.

Ростов‐на‐Дону 2010г.

СОДЕРЖАНИЕ.

Введение……………………………………………………………….…………………………………………………………………….. 3

Постановка задачи…………….……………………………….……………………………………………………………………….. 5

Алгоритмизация………………….………….…………………………………………………………………………………………… 6

Выполнение поставленной задачи…………....………………………………………………………………………………. 9

Ручной просчёт………….…………………………………………………………………………………………………….. 9

Тест программы………………………..……………………………………………………………………………………. 11

Код программы…………………….…….…………………………………………………………………………………………….. 13

Приложение……………………………………..……………………………………………………………………………………….. 16

Список литературы……………………………………………………………………………………………………………………. 18 ВВЕДЕНИЕ.

Граф - исключительно популярный объект, минимально удаленный как от своего целостного пространственного образа, так и от описания по всем правилам теории множеств. Всякий раз, когда с задачей удается связать граф, обсуждение резко упрощается и большие фрагменты словесного описания заменяются манипуляциями с картинками.

Ю.И.Манин.

Многосвязная структура характеризуется следующими свойствами: (1) каждый элемент структуры содержит произвольное число направленных связей с другими элементами (или ссылок на другие элементы); (2) с каждым элементом может связываться произвольное количество других элементов (каждый элемент может быть объектом ссылки произвольного количества других элементов); (3) каждая связь в структуре имеет не только направление, но и вес. Такую многосвязную структуру называют сетевой структурой или сетью. Заметим, что логически сеть эквивалентна взвешенному ориентированному графу общего вида, и поэтому вместо термина "сеть" часто употребляются термины "графовая структура", или даже просто "граф".

Особое значение сетевые структуры приобрели в системах искусственного интеллекта, в которых они адекватно отражают логику организации данных и сложные отношения, возникающие в таких системах между различными элементами данных. В этих системах сетевые структуры применяются для построения семантических сетей, фреймов и других логических конструкций, необходимых для представления знаний, образования понятий и осуществления логических выводов.

Кратчайшие пути в графе. Алгоритм Форда-Беллмана.

Мы взбираемся на вершину, откуда можем бросить гордый взгляд назад и оценить пройденный путь.

П.Буль.

Существует большое количество практических задач, сводящихся к поиску кратчайших путей в графе. К их числу можно отнести: поиск кратчайшего расстояния между городами; поиск пути передачи информации, обеспечивающего минимальную стоимость или минимальное время передачи, или максимальную надежность при распространении информации в разветвленной сети.

Исходными данными для поиска кратчайшего пути в графе является матрица весов дуг заданного ориентированного графа. Это означает, что каждой дуге (u,v)E поставлено в соответствие некоторое вещественное число А(u,v), называемое весом данной дуги. Длину кратчайшего пути d(s,t) между вершинами s и t называют расстоянием от s до t (расстояние, определенное таким образом, может быть и отрицательным). Если не существует ни одного пути из s в t, то полагают d(s,t)=Ґ, где Ґ- некоторый символ.

Большинство алгоритмов поиска расстояний между двумя фиксированными вершинами s и t включают в себя следующие действия: по данной матрице весов дуг A*u,v] (u,vV) вычисляют некоторые верхние ограничения D*v+ на расстояние от s до всех вершин v. На каждом шаге, если D*v++A*u,v+<D*v+ оценку D*v+ улучшают: D*v+=D*u++A*u,v+. Процесс прекращается, когда дальнейшее улучшение ни одного из ограничений невозможно.

Алгоритм Форда-Беллмана позволяет найти расстояние от источника до всех вершин D[v]=d(s,v), vV ориентированного графа при условии, что граф не содержит контуров отрицательной длины (n - количество вершин в графе). Исходными данными для этого алгоритма являются матрица весов дуг A[u,v].

На рисунке 1 приведен: (а) граф; (б) соответствующая ему матрица весов дуг; (в) результаты работы алгоритма Форда-Беллмана.

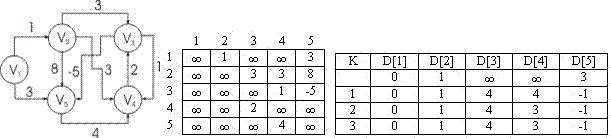
а б в

Рис. 1: Пример выполнения алгоритма Форда-Беллмана.

Приведенный алгоритм отыскания кратчайших путей в графах с отрицательными длинами дуг, принадлежащий Форду, Муру и Беллману, может служить одним из возможных способов обнаружения контуров отрицательной длины (или циклов в неориентированном графе).

ПОСТАНОВКА ЗАДАЧИ.

Даная задачу нужно рассматривать, как задачу оптимизации на графах. Она заключается в составлении программного кода на языке программирования Pascal, основываясь на алгоритме Форда-Беллмана, и её тестирования с ручном просчётом.

АЛГОРИТМИЗАЦИЯ.

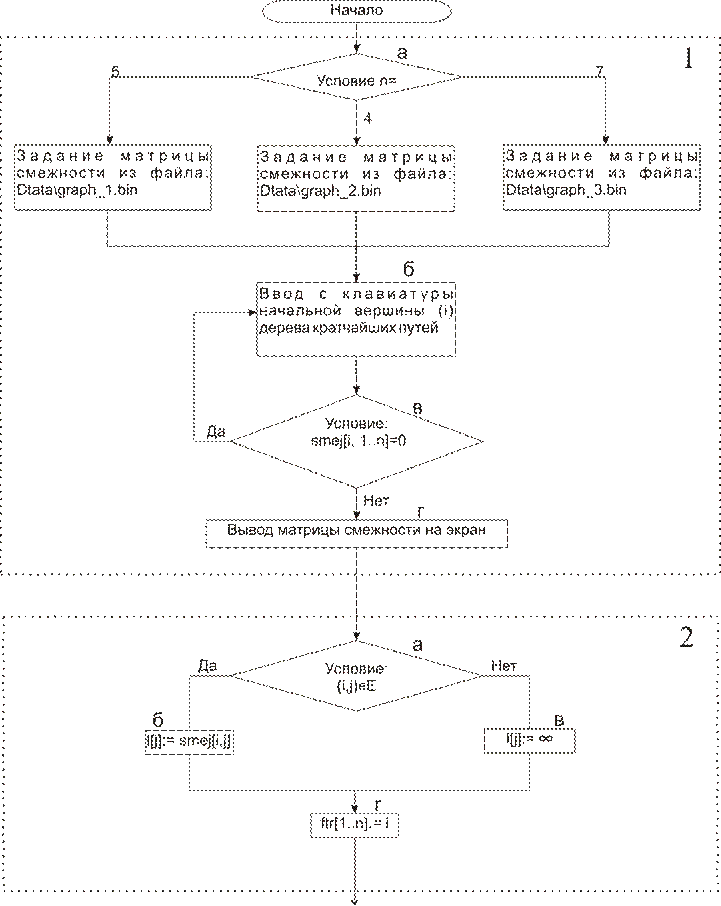
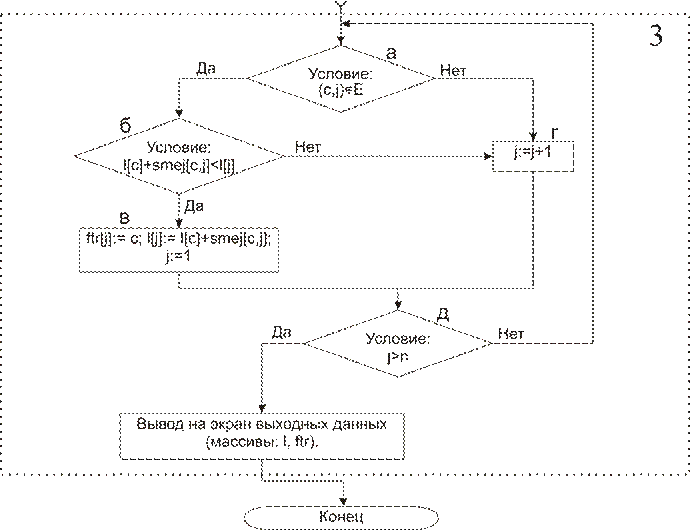
Рис 2: Блок-схема.

Пояснения к блок-схеме.

1. Задание входных данных.

а) Пользователь вводит число вершин в графе. И в зависимости какое число выбрал пользователь, задается матрица смежности из соответствующего файла.

б) Программа предлагает ввести начальную вершину i дерева кратчайших путей.

в) Если в i-ой строке матрицы смежности только 0, то есть из вершины i не выходит ни одной дуги, значит, вершину i нельзя рассматривать как начальную и переходим к пункту б.

г) Вывод матрицы смежности на экран, в табличном виде.

2. Инициализация выходных данных (массивы: кратчайших путей – l и предков – ftr).

а) Если существует дуга (i,j), то выполняется пункт б, иначе пункт в.

б) Расстояние от i до j – вес дуги (i,j).

в) Расстояние от i до j – бесконечно велико.

г) Предком всех вершин графа становиться начальная вершина i.

3. Построение дерева кратчайших путей в графе.

а) Если существует дуга (c,j), то существует путь i->c->j.

б) Если весовая величина пути i->c->j меньше уже установленного расстояния от вершины i до j, то выполняется пункт в, иначе к пункту г.

в) Предком вершины j становится промежуточная вершина c, а расстояние от i до j сумма весов дуг пути i->c->j.

г) Для рассмотрения берётся следующая после вершина после вершины j – j+1.

д) Если все вершины занесены в дерево, то производится вывод на экран выходных данных, если нет, то происходит переход к пункту а.

ВЫПОЛНЕНИЕ ПОСТАВЛЕНОЙ ЗАДАЧИ.

Ручной просчет.

Даны 3 ориентированных графа G₁ (5,12), G₂ (4,7), G₃ (7,14), заданные матрицами смежности. Построить для этих графов деревья кратчайших путей.

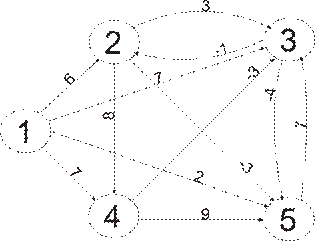Матрица смежности графа G₁ :

0 6 7 7 2

0 0 3 8 -3

0 -1 0 0 -4

0 0 -3 0 9

0 0 7 0 0

Массив предков: ftr = (0, 3, 4, 1, 3).

Массив расстояний от 1-ой начальной вершины до остальных: l = (0, 3, 4, 7, 0).

Рис. 3: Граф G₁ .

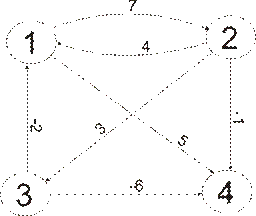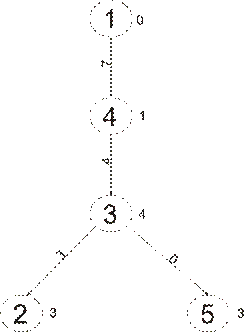
Рис. 4: Дерево кратчайших путей для графа G₁ .

Матрица смежности графа G₂ :

0 7 0 5

4 0 3 -1

-2 0 0 -6

0 0 0 0

Массив предков: ftr = (0, 1, 2, 3).

Массив расстояний от 1-ой

начальной вершины до остальных: Рис. 5: Граф G₂ .

l = (0, 7, 10, 4).

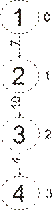
Рис. 6: Дерево кратчайших путей для графа G₂ .

Матрица смежности графа G₃ :

0 5 0 0 1 0 3

0 0 4 0 7 0 0

0 -4 0 0 -3 0 0

0 0 2 0 0 8 0

0 0 0 2 0 3 0

3 0 0 4 0 0 0

0 0 0 0 0 -1 0

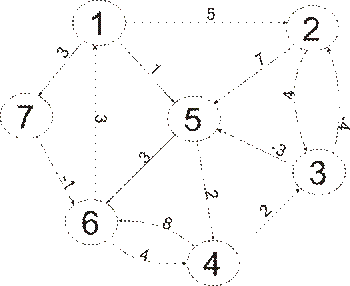
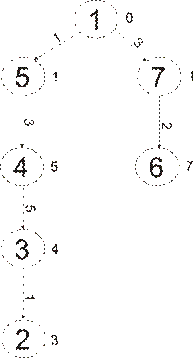
Рис. 7: Граф G₃ .

Массив предков: ftr = (0, 3, 4, 5, 1, 7, 1).

Массив расстояний от 1-ой начальной вершины до остальных:

l=(0,1, 5, 3, 1, 2, 1).

Рис. 8: Дерево кратчайших путей для графа G₃ .

Тест программы.

Рис. 9: Выполнение программы для графа G₁ .

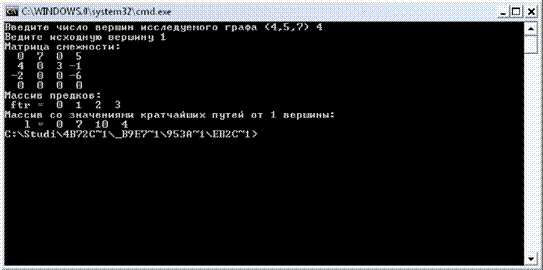
Рис. 10: Выполнение программы для графа G₂ .

Рис. 11: Выполнение программы для графа G₃ .

Рис. 12: Выполнение программы для графа G₂ .

В графе G₂ есть вершина, из которой нельзя построить дерево кратчайших путей – это 4 вершина, так как из неё не выходят дуги. Программа проводит проверку на заданную пользователем вершину, в нашем случае 4, и проводит проверку и обнаруживает, что 4 не подходит. Далее программа вновь предлагает ввести номер вершины и для введенной 2 успешно вычисляет выходные массивы. Правильность данных можно проверить, сверив их с деревом кратчайших путей для графа G₂ с начальной 2 вершиной на рисунке 13.

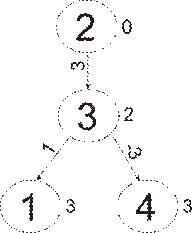
Рис. 13: Дерево кратчайших путей для графа G₂ с начальной вершиной №2.

КОД ПРОГРАММЫ.

program kurs; uses crt; const m=10;

type matrix= array [1..m, 1..m] of integer; massiv= array [1..m] of integer; var i,j,min,c,k,s,n: integer; v,l,ftr: massiv; smej: matrix; f: file of integer; label metka;

procedure vvod1(n: integer; var smej: matrix); begin

assign(f,'data/graph_1.bin');

reset(f); for i:=1 to n do for j:=1 to n do begin read(f,c); smej[i,j]:=c; end; close(f); end;

procedure vvod2(n: integer; var smej: matrix); begin

assign(f,'data/graph_2.bin');

reset(f); for i:=1 to n do for j:=1 to n do begin read(f,c); smej[i,j]:=c; end; close(f); end;

procedure vvod3(n: integer; var smej: matrix); begin

assign(f,'data/graph_3.bin');

reset(f); for i:=1 to n do for j:=1 to n do begin read(f,c); smej[i,j]:=c; end; close(f); end; Begin clrscr;

write('Введите число вершин исследуемого графа (4,5,7) '); read(n); case n of 5: vvod1(n,smej);

4: vvod2(n,smej); 7: vvod3(n,smej); end;

write('Ведите исходную вершину ');

metka: read(i); s:=0; for k:=1 to n do if not(smej[i,k]=0) then s:=1; if s=0 then begin writeln('Из этой вершины нет выходящих дуг.'); write('Bведите другую вершину '); goto metka end; writeln('Матрица смежности: '); for k:=1 to n do begin for s:=1 to n do if smej[k,s]<0 then write(' ',smej[k,s]) else write(' ',smej[k,s]); writeln;

end;

for j:=1 to n do begin l[j]:=smej[i,j]; ftr[j]:=i;

if l[j]=0 then l[j]:=99; end;

l[i]:=0; for j:=1 to n do begin min:=l[j]; for k:=1 to n do if not(smej[k,j]=0) and not(k=i) then if smej[k,j]<min then begin

c:= k; min:=smej[k,j]; end; v[j]:= l[c]+smej[c,j]; if v[j]<l[j] then

begin

l[j]:=v[j]; ftr[j]:=c; j:=1; end;

End;

ftr[i]:=0; l[i]:=0;

writeln('Массив предков: ');

write(' ftr ='); for k:= 1 to n do

write(' ',ftr[k]); writeln;

writeln('Массив со значениями кратчайших путей от ',i,' вершины: '); write(' l ='); for k:=1 to n do if l[k]<0 then write(' ',l[k]) else write(' ',l[k]); End.

ПРИЛОЖЕНИЕ.

Коды программ используемые для создания файлов с данными. Для 1-го графа. program graph1; uses crt; const n=5;

type matrix= array [1..n, 1..n] of integer;

var i,j,c,n: integer; smej: matrix; f: file of integer; Begin clrscr;

smej[1,2]:=6; smej[1,3]:=7; smej[1,4]:=7; smej[1,5]:=2; smej[2,3]:=3; smej[2,4]:=8; smej[2,5]:=-3; smej[3,2]:=-1; smej[3,5]:=-4; smej[4,3]:=-3; smej[4,5]:=9; smej[5,3]:=7; assign(f,'data/graph_1.bin');

rewrite(f); for i:=1 to n do for j:=1 to n do begin c:=smej[i,j]; write(f,c); end; close(f); End.

Для 2-го графа. program graph2; uses crt; const n=4;

type matrix= array [1..n, 1..n] of integer;

var i,j,c,n: integer; smej: matrix; f: file of integer; Begin clrscr; smej[1,2]:=7; smej[1,4]:=5; smej[2,1]:=4;smej[2,3]:=3; smej[2,4]:=-1; smej[3,1]:=-2; smej[3,4]:=-6; assign(f,'data/graph_2.bin');

rewrite(f); for i:=1 to n do for j:=1 to n do begin c:=smej[i,j]; write(f,c); end; close(f); End.

Для 3-го графа. program kurs; uses crt; const n=7;

type matrix= array [1..n, 1..n] of integer;

var i,j,c,n: integer; smej: matrix; f: file of integer; Begin clrscr; smej[1,2]:=5; smej[1,5]:=1; smej[1,7]:=3; smej[2,3]:=4; smej[2,5]:=7; smej[3,2]:=-4; smej[3,5]:=-3; smej[4,3]:=2; smej[4,6]:=8; smej[5,4]:=2; smej[5,6]:=3; smej[6,1]:=3; smej[6,4]:=4; smej[7,6]:=-1; assign(f,'data/graph_3.bin'); rewrite(f); for i:=1 to n do for j:=1 to n do begin c:=smej[i,j]; write(f,c); end; close(f); End.

СПИСОК ЛИТЕРАТУРЫ.

В.Н. Землянухин, Л.Н. Землянухина – Задачи оптимизации на графах. 2009г.

А.Е. Костин, В.Ф. Шаньгин – Организация и обработка структур данных в вычислительных системах. Учебное пособие для вузов. 1987г.

Ж. Трамбле, П. Соренсон – Введение в структуры данных. 1982г.

Ф. Харари – Теория графов. 1973г.

В. Липский – Комбинаторика для программистов. 1988г.

В.Л. Бурковский, Л.В. Холопкина, Н.Л. Райхель, О.Я. Кравец – Методы моделирования и анализа вычислительных систем. Учебное пособие. 1996г.

В.А. Евстигнеев, В.Н. Касьянов – Графы в программировании: обработка, визуализация и применение.