Контрольная работа №2

Вариант №9

Задание №1

Найти неопределенные интегралы:

1)

2)

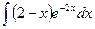
Решение:

Для нахождения интеграла  применяем метод замены переменной.

Получим 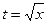 тогда 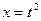   найденные значения подставляем в интеграл

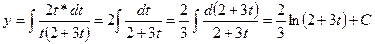 возвращаемся к х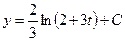 

Ответ: .

Задание №2

Найти неопределенные интегралы:

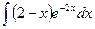
Решение:

Для нахождения интеграла 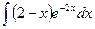 воспользуемся методом интегрирования по частям.

Получим u=(2-x) dv= находим du=-dx

.

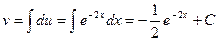По формуле интегрирования по частям 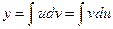 получаем Ответ: искомый интеграл равен .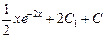

Задание №3

Вычислить определенные интегралы:

Решение:

Для вычисления интеграла y= применим замену переменной.

Примем  и dx=2t*dt. Если х=4, то t=2, если х=9, то t=3.

После замены переменной получаем

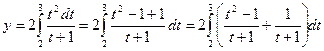
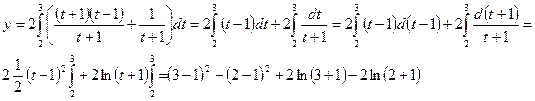
Ответ: =

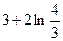
Задание №4

Вычислить определенные интегралы:

Решение:

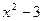 представим  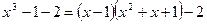тогда

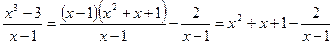
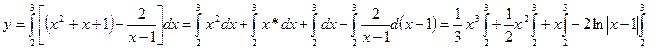
Ответ: =.

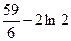Задание №5

Вычислить объем тела, образованного вращением вокруг оси Oy фигуры, ограниченной линиями:

.

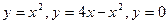Решение:

Для схематического построения фигуры ограниченной указанными линиями проведем анализ графиков .

Кривая 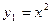является параболой с вершиной в начале координат, симметричной относительно оси ординат.

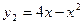- так же парабола координату х вершины кривой 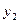найдем из уравнения  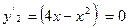, 4-2х=0,    . Ордината вершины определяется из 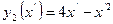,  ,   координаты вершины А(2;4).

Точки пересечения кривой 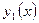 с осью х определяется из о=4х-.

Две точки х=0 и х=4 то есть О(0;0) и B(4;0).

Общие точки пересечения кривых определяется из совместного решения уравнений , ,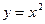

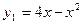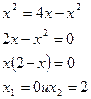
Таким образом, пересечение лини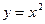й  и 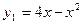 происходит в начале координат и в вершине параболы 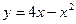 в точке А(2;4).

Из построенного графика определяем, что объем тела образуется вращением плоской фигуры вокруг оси Oy ограниченной с низу осью х справа кривой 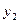от точек А до В , слева линией  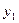от точки А до точки О то есть плоской фигуры ОАВ.

Задание №6

Пользуясь разложением подынтегральной функции в ряд Маклорена, вычислить интеграл 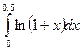 с точностью до 0,001. Вычислить этот же интеграл, используя формулу Ньютона-Лейбница.

Сравнить полученные результаты.

Решение:

Ряд Маклорена представлен формулой:

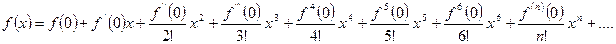
В данном случае  f(x)=ln(1+x).

При x=0 функция f(0)=ln(1+0), f(0)=ln1, а ln1=0 получаем f(0)=0.

Находим производные от функции f(x)=ln(1+x) и определяем их значения при x=0,

,

 ,

,

  ,

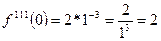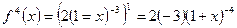 при х=0,

,

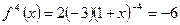Для ясности выпишем значения производных при х=0 значение f(0)^

Эти значения подставим в формулу ряда Маклорена:

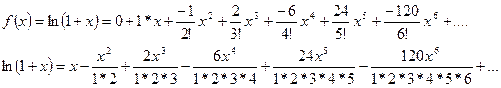
Окончательно получаем разложение функции ln(1+x) так как остальные члены разложения от n и далее n+1 отброшены:

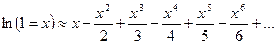
Вычисляем интеграл:

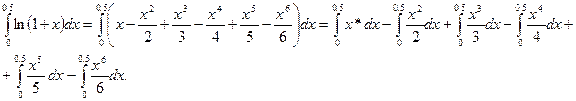
Вычислим каждый интеграл по отдельности:

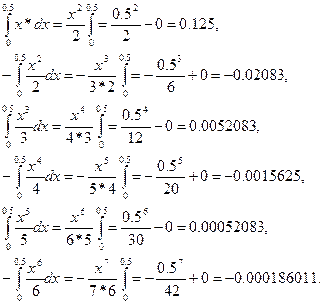
Заменим результаты вычисления вряд:

По условию задачи погрешность задана .

Для достижения заданной погрешности последние члены суммы ряда можно отбросить и первый отброшенный член ряда с которого отбрасываются все последующие остальные, будет пятый (ибо погрешность не превышает абсолютной величины первого отброшенного члена).

0,00052083<0.001

Окончательно

,

а).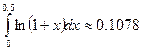

Вычисляем этот же интеграл другим способом без разложения вряд по формуле Ньютона-Лейбница.

Дано .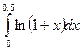

Решение:

Применяем интегрирования по частям.

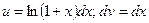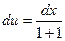Пусть тогда  v=x.

Применим формулу по частям получаем

.

Для нахождения интеграла 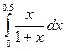 делаем подстановку 1+x=t тогда dx=dt, x=t-1 .

Находим новые пределы интегрирования: если х=0, то t=1; если х=0,5, то t=1.5

.

Вычислим  определяем значение интеграла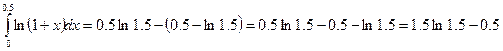

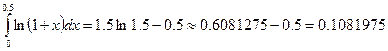
б) с заданной погрешностью сравнивая результаты вычислений интегралов а и б получим 0,1082-0,1078=0,0004.

Ответ: При вычислении интеграла 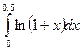 методом приближенных вычислений получаем результат с данной точностью: y=0,1078.

При вычислении интеграла по формуле Ньютона-Лейбница получаем результат y=0,1082.

Расхождения составляет .

Точный без погрешностей результат 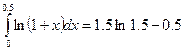.