Содержание

Задача 1. 3

Задача 2. 4

Задача 3. 9

Задача 4. 11

Задача 5. 14

Список литературы.. 15

Задача 1.

Один рабочий тратит на изготовление одной детали 2 минуты, а второй – 6 минут.

Определить:

1.     средние затраты времени на изготовление 1 детали (минут).

2.     количество деталей, изготовленные за первые 2 часа рабочего дня.

3.     общие трудозатраты и время, необходимое на изготовление первой партии из 100 деталей.

Решение:

Средняя арифметическая простая (невзвешенная) равна сумме отдельных значений признака, деленной на число этих значений.

Отдельные значения признака называют вариантами и обозначают  через х (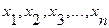); число единиц совокупности обозначают через n, среднее значение признака - через . Следовательно, средняя арифметическая простая равна:

1.

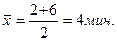
2.

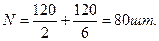
3.

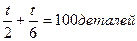
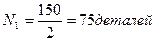
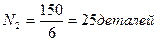
Ответ: , , , ,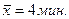

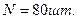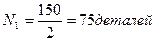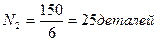
Задача 2.

По сельскохозяйственному предприятию имеются следующие данные о валовом сборе зерновых культур.

Год

Валовый сбор, тонн

1990

162

1991

178

1992

180

1993

183

1994

185

1995

184

1996

187

1997

190

1998

192

1999

196

2000

199

1)                              Построить уравнение общей тенденции валового сбора в форме линейного тренда методами:

а) первых разностей (абсолютных цепных приростов);

б) методом средних;

в) аналитического выравнивания методом наименьших квадратов.

2)                              Отразить на графике фактический валовой сбор зерновых, его основную тенденцию и ожидаемое значение на ближайшую перспективу.

Решение:

Абсолютные цепные приросты валового сбора определяются по формуле:

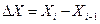
где     – величина валового сбора в i-тый год, тонн;

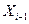          – величина валового сбора в предыдущий год, тонн.

Год

Валовый сбор, тонн

Абсолютные цепные приросты, тонн

1990

162

-

1991

178

16

1992

180

8

1993

183

3

1994

185

2

1995

184

-1

1996

187

3

1997

190

3

1998

192

2

1999

196

4

2000

199

3

Способ скользящей средней состоит в том, что вместо каждого уровня исходного ряда берутся средние из уровней рядом стоящих периодов, причем период осреднения все время меняется: из него вычитается один член и прибавляется следующий. Суть метода заключается в расчете средней величины из 3 (5 и более) уровней ряда, образованных последовательным исключением начального члена ряда и замещением следующим по порядку.  

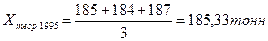
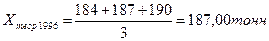
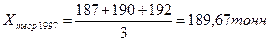
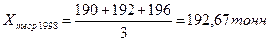
Таблица – Фактический и теоретический показатели валового сбора

Годы

Фактический валовый сбор, тонн

Теоретический валовый сбор, тонн

1990

162

-

1991

178

173,33

1992

180

180,33

1993

183

182,67

1994

185

184,00

1995

184

185,33

1996

187

187,00

1997

190

189,67

1998

192

192,67

1999

196

195,67

2000

199

-

Графическое изображение динамики показателей валового сбора представлены на рисунке 1.

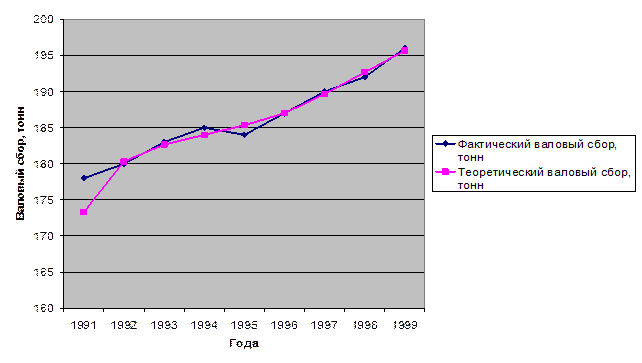
Рисунок 1 – Динамика показателей валового сбора

Таблица – Аналитическое выравнивание

Годы

Показатель

Отклонение от центра (время)

Квадрат времени

Произведение показателя на время

Выровненные уровни

n

Y

t

t2

Y*t

yt =185,09-2,81*t

1990

162

5

25

810

171,04

1991

178

4

16

712

173,85

1992

180

3

9

540

176,66

1993

183

2

4

366

179,47

1994

185

1

1

185

182,28

1995

184

0

0

0

185,09

1996

187

-1

1

-187

187,9

1997

190

-2

4

-380

190,71

1998

192

-3

9

-576

193,52

1999

196

-4

16

-784

196,33

2000

199

-5

25

-995

199,14

Итого

2036

0

110

-309

-

Уравнение прямой линии имеет вид (тренд):

yt = A+B*t,

где    А = ∑Y / n

B = ∑ (Y*t)/ ∑ t2

А = 2036 / 11 =  185,09

В = - 309 / 110 = - 2,81

Уравнение прямой: yt = 185,09-2,81*t,

Графическое изображение динамики показателей представлено на рисунке 2.

Рисунок 2 – Динамика показателей валового сбора

Задача 3.

В результате 5 % механической выборки в отделении банка получено следующее распределение вкладов по срокам хранения:

Группы вкладов по сроку хранения, дней

Количество вкладов

До 30

98

30 – 60

140

60 – 90

175

90 – 180

105

180 – 360

56

360 и более

26

Определить:

1)    средний срок хранения вкладов по данным выборки;

2)    долю вкладов со сроком хранения более 180 дней по данным выборки;

3)    с вероятностью 0,954 пределы, в которых можно ожидать среднюю продолжительность хранения вклада в целом по отделению банка.

Группы вкладов по сроку хранения, дней

Коли-

чество вкладов

Середина интервала

До 30

98

15

30 – 60

140

45

60 – 90

175

75

90 – 180

105

135

180 – 360

56

270

360 и более

26

450

Итого

600

-

Средняя арифметическая взвешенная себестоимости единицы продукции определяется по формуле:

,

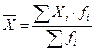где 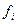    – значение частоты повторения признака.

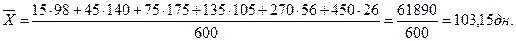
Доля единиц, которая обладает данным признаком выборочной совокупности:

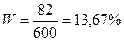
Абсолютная ошибка выборки:

При вероятности 0,954 t=2.

Так как обследовано 5% вкладов, то полное количество вкладов составляет N=600/0,05=12000

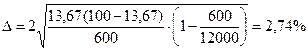
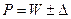 - доверительный интервал.

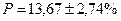
Ответ: средний срок хранения вкладов по данным выборки получается равным 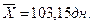; доля вкладов со сроком хранения более 180 дней по данным выборки получается равна; пределы, в которых можно ожидать среднюю продолжительность хранения вклада в целом по отделению банка составляют от 10,93% до 16,41%.

Задача 4.

Имеются данные о спросе на книжную продукцию и структуре оборота книжного издательства в отчетном году:

Стратегическая единица

Спрос на продукцию, тыс. экз.

Доля в общем обороте издательства, %

1. Классика

20

0

2. Детская литература

100

1,0

3. Зарубежный детектив

60

49,5

4. Российский детектив

120

20,5

5. Женский роман

90

6,8

6. Фантастика

50

0

7. Приключения

30

1,0

8. Специальная литература

110

14,3

9. Рекламная продукция

60

4,9

10. Прочая литература

80

2,0

Определите уровень согласованности между спросом на книжную продукцию и структурой оборота издательства с помощью коэффициентов корреляции Спирмена и Фехнера.

Стратегическая единица

Ранги

По спросу на продукцию

По доле в общем обороте издательства

1. Классика

1

1

0

0

2. Детская литература

2

8

6

36

3. Зарубежный детектив

3

4,5

1,5

2,25

4. Российский детектив

4

10

6

36

5. Женский роман

5

7

2

4

6. Фантастика

6

3

-3

9

7. Приключения

7

2

-5

25

8. Специальная литература

8

9

1

1

9. Рекламная продукция

9

4,5

-4,5

20,25

10. Прочая литература

10

6

-4

16

Итого

10

10

-

149,5

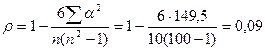
Так как коэффициент ранговой корреляции положительное число, то связь прямая. С увеличением спроса на продукцию, доля в общем обороте издательства увеличивается.

Спрос на продукцию, тыс. экз, х

Доля в общем обороте издательства, у

х2

у2

ху

20

0

400

0

0

100

1

10000

1

100

60

49,5

3600

2450,25

2970

120

20,5

14400

420,25

2460

90

6,8

8100

46,24

612

50

0

2500

0

0

30

1

900

1

30

110

14,3

12100

204,49

1573

60

4,9

3600

24,01

294

80

2

6400

4

160

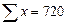
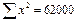
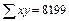
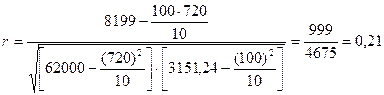
Связь слабая, т.к. r < 0,3.

Ответ: , .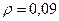

Задача 5.

Имеются данные областного комитета государственной статистики об изменении цен в текущем году по сравнению с предшествующим годом:

Изменение цен, %

1. Платные услуги

+62,3

2. На продовольственные товары

+22,4

3. На непродовольственные товары

+20,1

Рассчитайте индекс потребительских цен (ИПЦ), учитывая, что в текущем году сформировалась следующая структура потребления (структура потребительской корзины).

Платные услуги

41,0 %

Продовольственные товары

31,8 %

Непродовольственные товары

27,2 %

ИПЦ рассчитывается по формуле Ласпейреса.

,

где    – цена текущего периода;

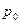         – цена базового периода;

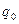– количество товара в базовом году.

Ответ:

Список литературы

1.     Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник. – М.: Финансы и статистика, 1996 г.

2.     Ефимова М.Е., Петрова Е.В., Румянцев В.М. Общая теория статистики: Учебник. – М.: Финансы и статистика, 1996 г.

3.     Спирина А.А., Башина О.Э. Общая теория статистики. – М.: Финансы и статистика, 1997 г.

4.     Шмойлова Р.А. Теория статистики: Учебник. – М.: Финансы и статистика, 2000 г.

5.     Харченко Л.П., Долженкова В.Г., Ионин В.Г. Статистика: Учебное пособие. – М.: ИНФРА-М, 2003 г.