Вопрос 5.

УСЛОВНЫЕ ВЕРОЯТНОСТИ

1.             (2)

Игральную кость подбросили один раз. Рассмотрим два события: A – «выпало четное число очков»,  B – «выпало 2 очка». Найти условную вероятность .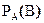

            Ответы:       1.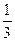

                                                              

2.             (2)

Игральную кость подбросили один раз. Рассмотрим два события: A – «выпало четное число очков»,  B – «выпало 3 очка». Найти условную вероятность .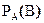

                                                               3. 0 

                                                              

3.             (2)

Игральную кость подбросили один раз. Рассмотрим два события: A – «выпало нечетное число очков»,  B – «выпало 3 очка». Найти условную вероятность .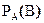

            Ответы:       1.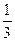

                                                              

4.                   (2)

В урне 5 белых и 3 черных шара. Из урны извлекают последовательно два шара.

Рассмотрим два события: A – «первый извлеченный шар – белый», B – «второй извлеченный шар белый». Найти условную вероятность P_A(B).

                                2.

                               

5.                   (2)

В урне 5 белых и 3 черных шара. Из урны извлекают последовательно два шара. Рассмотрим два события: A – «первый извлеченный шар – белый», B – «второй извлеченный шар черный». Найти условную вероятность P_A(B).

                                3.

           

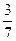
6.                   (2)

В урне 5 белых и 3 черных шара. Из урны извлекают последовательно два шара. Рассмотрим два события: A – «первый извлеченный шар – черный», B – «второй извлеченный шар белый». Найти условную вероятность P_A(B).

                                3.

               

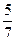
7.                   (2)

В урне 5 белых и 3 черных шара. Из урны извлекают последовательно два шара. Рассмотрим два события: A – «первый извлеченный шар – черный»,  B – «второй извлеченный шар черный». Найти условную вероятность P_A(B).

                                2.

                               

8.                   (4)

Монету подбросили два раза. Рассмотрим два события: A – «выпали два орла», B – «первый раз выпал орел». Найти условную вероятность P_B(A).

Правильный ответ: 0,5.

9.                   (4)

Монету подбросили два раза. Рассмотрим два события: A – «выпали два орла»,  B – «второй раз выпал орел». Найти условную вероятность P_B(A).

Правильный ответ: 0,5.

10.                (2)

Подбросили две игральные кости. Рассмотрим два события: A – «сумма выпавших очков более 10»,  B – «сумма выпавших очков равна 12». Найти условную вероятность P_A(B).

Ответы:  1.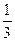

                               

11.                (2)

Подбросили две игральные кости. Рассмотрим два события: A - «сумма выпавших очков более 10»,  B – «сумма выпавших очков равна 12». Найти условную вероятность P_B(A).

                                3. 1

               

12.                (2)

Подбросили две игральные кости. Рассмотрим два события: A - «сумма выпавших очков более 10»,  B – «сумма выпавших очков равна 11». Найти условную вероятность P_A(B).

                                2.

                       

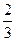
13.                (2)

Подбросили две игральные кости. Рассмотрим два события: A - «сумма выпавших очков более 10»,  B – «сумма выпавших очков равна 11». Найти условную вероятность P_B(A).

                                3. 1

               

14.                (2)

Подбросили две игральные кости. Рассмотрим два события: A - «сумма выпавших очков менее 4»,  B – «сумма выпавших очков равна 3». Найти условную вероятность P_B(A).

                                3. 1

               

15.                (2)

Подбросили две игральные кости. Рассмотрим два события: A - «сумма выпавших очков менее 4»,  B – «сумма выпавших очков равна 3». Найти условную вероятность P_A(B).

Ответы:  1.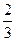

                               

16.                (4)

Подбросили две игральные кости. Рассмотрим два события: A - «сумма выпавших очков четна»,  B – «сумма выпавших очков равна 6». Найти условную вероятность P_B(A).

               Правильный ответ: 1.

17.                (4)

Подбросили две игральные кости. Рассмотрим два события: A - «сумма выпавших очков четна», B – «сумма выпавших очков равна 5». Найти условную вероятность P_B(A).

               Правильный ответ: 0.

18.                (4)

Подбросили две игральные кости. Рассмотрим два события: A - «сумма выпавших очков четна»,  B – «сумма выпавших очков равна 5». Найти условную вероятность P_A(B).

               Правильный ответ: 0.

19.                 (4)

Подбросили две игральные кости. Рассмотрим два события: A - «сумма выпавших очков нечетна»,  B – «сумма выпавших очков равна 5». Найти условную вероятность P_B(A).

               Правильный ответ: 1.

20.                (4)

Подбросили две игральные кости. Рассмотрим два события: A - «сумма выпавших очков нечетна»,  B – «сумма выпавших очков равна 12». Найти условную вероятность P_B(A).

               Правильный ответ: 0.

21.                (4)

Подбросили две игральные кости. Рассмотрим два события: A - «сумма выпавших очков нечетна»,  B – «сумма выпавших очков равна 6». Найти условную вероятность P_A(B).

               Правильный ответ: 0.

22.                 (2)

Игральную кость подбросили один раз. Рассмотрим два события: A – «выпало 2 очка»,  B – «выпало четное число очков». Найти условную вероятность .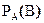

           

                                               3. 1