Вопрос 4.
ТЕОРЕМА УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ
(ЗАДАЧИ)
Зависимые
события.
1. (2)
Ребенок
играет с буквами разрезной азбуки. У него 3 буквы «А», 2 буквы «Р» и 1 буква
«Т». Какова вероятность того, что при случайном расположении букв в ряд
получится слово «АРАРАТ»?
3.

2. (2)
На шести карточках написаны
буквы А, В, К, М, О, С. После перемешивания вынимают наугад одну карточку за
другой и раскладывают по порядку. Найти вероятность того, что при этом
получится слово «МОСКВА»
Ответы: 1. 
3. (2)
Пять цифр 1; 1; 1; 2; 2 написаны
на отдельных карточках. Найти вероятность того, что при случайном расположении
карточек в ряд получится число 11221.
2.

4. (2)
На карточках написаны буквы А,
А, Л, М, П, Р. Ребенок наугад берет 5 карточек и выкладывает их в ряд. Какова
вероятность того, что получится слово «ЛАМПА».
2.

5. (2)
Из
карточек с буквами А, Б, В, Г, Д наугад одна за другой выбирают три карточки и
располагают их в ряд в порядке появления. Какова вероятность того, что
получится слово «ДВА»?
Ответы: 1.
6. (4)
В урне 2 красных, 3 желтых и один
зеленый шар. Из урны извлекают три шара, не возвращая их обратно. Найти
вероятность того, что шары окажутся извлеченными в последовательности: красный,
желтый, зеленый.
Правильный ответ: 0,05.
7. (4)
Некто забыл
последние две цифры телефонного номера, но помнит, что они нечетные и
различные. Какова вероятность того, что он сразу наберет нужный номер, если
будет набирать эти цифры случайно?
Правильный
ответ: 0,05.
8. (2)
Некто забыл
последние две цифры телефонного номера, но помнит, что они различные. Какова
вероятность того, что он сразу наберет нужный номер, если будет набирать эти
цифры случайно?
Ответы: 1.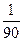
Независимые события.
1. (4)
Первый стрелок попадает в цель с вероятностью 0,9, а второй
с вероятностью 0,8. Каждый стрелок
сделал по одному выстрелу. Какова вероятность того, что оба промахнулись?
Правильный ответ: 0,02.
2. (4)
Первый стрелок попадает в цель с вероятностью 0,9, а
второй с вероятностью 0,8. Каждый
стрелок сделал по одному выстрелу. Какова вероятность того, что оба попали?
Правильный ответ: 0,72.
3. (4)
Первый стрелок попадает в цель с вероятностью 0,9, а
второй с вероятностью 0,8. Каждый
стрелок сделал по одному выстрелу. Какова вероятность того, что один из них
промахнулся?
Правильный ответ: 0,26.
4. (4)
Баскетболист дважды бросает мяч
в корзину. Вероятность попадания при первом броске равна 0,6, а при втором –
0,8. Какова вероятность того, что цели достигнет только один бросок?
Правильный ответ: 0,44.
5. (4)
Баскетболист дважды бросает мяч
в корзину. Вероятность попадания при первом броске равна 0,6, а при втором –
0,8. Какова вероятность того, что цели достигнет только первый бросок?
Правильный ответ: 0,12.
6. (4)
Баскетболист дважды бросает мяч
в корзину. Вероятность попадания при первом броске равна 0,6, а при втором –
0,8. Какова вероятность того, что цели достигнет только второй бросок?
Правильный ответ: 0,32.
7. (4)
Вероятности попадания в цель при
стрельбе из трех орудий равны соответственно 0,7, 0,8 и 0,5. Какова
вероятность хотя бы одного попадания при
одном залпе из всех трех орудий?
Правильный ответ: 0,97.
8. (4)
Вероятности попадания в цель при
стрельбе из трех орудий равны соответственно 0,7, 0,8 и 0,5. Какова
вероятность того, что первое и второе
орудия промахнулись?
Правильный ответ: 0,06.
9. (4)
Вероятности попадания в цель при
стрельбе из трех орудий равны соответственно 0,7, 0,8 и 0,5. Какова вероятность
хотя бы одного промаха при одном залпе
из всех трех орудий?
Правильный ответ: 0,72.
10. (4)
Вероятности попадания в цель при
стрельбе из трех орудий равны соответственно 0,7, 0,8 и 0,5. Какова вероятность
того, что третье орудие промахнулось?
Правильный ответ: 0,5.
Описание правильного ответа:
11. (4)
Три стрелка выстрелили по цели. Вероятность попадания
в цель для первого стрелка равна 0,7, для второго 0,8, для третьего 0,9. Найти
вероятность того, что только второй
стрелок попал в цель.
Правильный ответ: 0,024.
12. (4)
Три стрелка выстрелили по цели. Вероятность попадания
в цель для первого стрелка равна 0,7, для второго 0,8, для третьего 0,9. Найти
вероятность хотя бы одного попадания в цель.
Правильный ответ: 0,994.
13. (4)
Три стрелка выстрелили по цели. Вероятность попадания
в цель для первого стрелка равна 0,7, для второго 0,8, для третьего 0,9. Найти
вероятность хотя бы одного промаха.
Правильный ответ: 0,496.
14. (2)
В урне 2 красных, 3 желтых и один
зеленый шар. Из урны поочередно извлекают три шара, фиксируют их цвет и
возвращают обратно. Найти вероятность того, что шары окажутся извлеченными в
последовательности: красный, желтый, зеленый.
3. 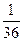
15. (4)
Три стрелка сделали по одному выстрелу по мишени. Вероятности
попадания для стрелков равны соответственно 0,7; 0,6 и 0,4. Найти вероятность
того, что в мишени хотя бы одна пробоина.
Правильный ответ: 0,928.
16. (4)
Три стрелка сделали по одному выстрелу по мишени.
Вероятности попадания для стрелков равны соответственно 0,7; 0,6 и 0,4. Найти
вероятность того, что в мишени не более двух пробоин.
Правильный ответ: 0,832.
17. (2)
Бросают две игральные
кости. Найти вероятность того, что в сумме выпадет 11 очков.
Ответы: 1. 
18. (2)
Бросают две игральные
кости. Найти вероятность того, что в сумме выпадет 12 очков.
2.
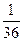
19. (2)
Бросают две игральные
кости. Найти вероятность того, что только
на одной кости выпадет 6.
2.
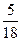
20. (4)
Некто забыл
последние две цифры телефонного номера, но помнит, что первая цифра четная, а
вторая нечетная. Какова вероятность
того, что он сразу наберет нужный номер, если будет набирать эти цифры
случайно?
Правильный
ответ: 0,04.