СОДЕРЖАНИЕ
Задача 4. 3
Задача 14. 6
Задача 24. 7
Задача 34. 9
Задача 44. 13
СПИСОК ЛИТЕРАТУРЫ.. 15
Задача 4
В приведенных ниже
данных:
1. Построить интервальный
ряд распределения (образовать четыре группы с равными интервалами).
2. Для полученного
интервального ряда вычислить:
а) среднюю
арифметическую;
б) среднее квадратическое
отклонение;
в) коэффициент вариации.
3. Изобразить полученный
ряд графически.
Данные:
Количество решенных задач
двадцатью студентами:
10 5
8 9 9
8 6 4 11 10 5 9
12 11
7 9 8
12 11 11
Решение
Сначала
определяем величину интервала по
формуле:
Δ =  ,
(1)
,
(1)
где
хmax – максимальное значение
количественного признака;
xmin –
минимальное значение количественного признака;
n – число
намечаемых групп.
Δ = 
Таким
образом, получаем четыре группы:
1
группа: 4 – 6
2
группа: 6 – 8
3
группа: 8 – 10
4
группа: 10 – 12
Принцип
группировки выбираем «включительно».
Далее
проводим группировку. Для этого составим таблицу 1.
Таблица 1
Интервальный
вариационный ряд распределения количества решаемых задач между 20-ю студентами
|
№ п/п
|
Группы по числу решаемых
задач
|
Число студентов (частота
f)
|
В процентах к итогу, %
|
Накопленная частота S
|
|
1
|
4 – 6
|
4
|
20,0
|
4
|
|
2
|
6 – 8
|
4
|
20,0
|
8
|
|
3
|
8 – 10
|
6
|
30,0
|
14
|
|
4
|
10 – 12
|
6
|
30,0
|
20
|
|
ИТОГО:
|
20
|
100,0
|
─
|
Для
данного интервального вариационного ряда используется формула средней
арифметической взвешенной:
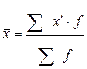 (2)
(2)
Среднее квадратическое
отклонение определяется по формуле:
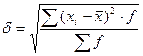 (3)
(3)
Коэффициент
вариации характеризует относительную меру колеблемости и определяется по
формуле:
 (4)
(4)
Для
удобства расчетов составим вспомогательную таблицу 2.
Таблица 2
|
Группы по числу решаемых
задач
|
Число студентов
(f)
|
Централь-ная варианта
(х)
|
Накоп-ленная частота (S)
|
х*f
|
|х-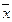 | |
|
|х-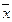 |2 |2
|
|х-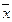 |2* f |2* f
|
|
4 – 6
|
4
|
5
|
4
|
20
|
3,4
|
11,56
|
46,24
|
|
6 – 8
|
4
|
7
|
8
|
28
|
1,4
|
1,96
|
7,84
|
|
8 – 10
|
6
|
9
|
14
|
54
|
0,6
|
0,36
|
2,16
|
|
10 – 12
|
6
|
11
|
20
|
66
|
2,6
|
6,76
|
40,56
|
|
ИТОГО:
|
20
|
─
|
─
|
168
|
─
|
─
|
96,8
|
Средняя
арифметическая взвешенная составит:
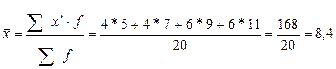 решаемых задач
решаемых задач
Среднее квадратическое
отклонение составит:
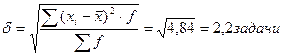
Коэффициент
вариации составит:
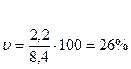
Коэффициент
вариации меньше 30 %, значит, совокупность однородная и средняя – надежная.
Интервальный
вариационный ряд распределения изображается при помощи гистограммы
распределения.
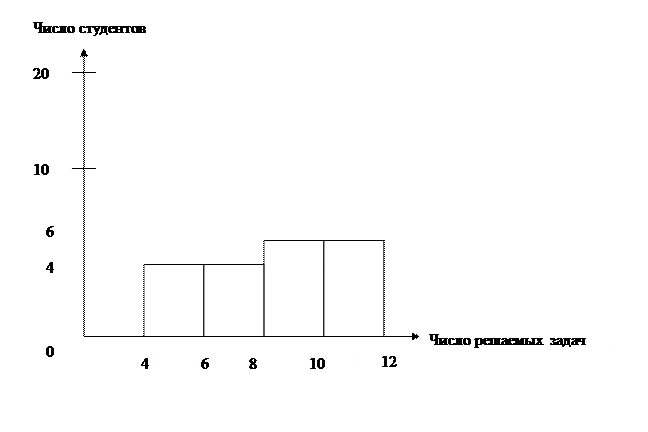
Рис. 1 Гистограмма распределения числа решаемых задач
Задача 14
Имеются данные о посевной
площади и урожайности пшеницы
|
Номер хозяйства
|
Предыдущий год
|
Отчетный год
|
|
Урожайность, ц/га
|
Посевная площадь
|
Урожайность, ц/га
|
Валовый сбор, ц
|
|
1
|
30,0
|
160
|
31,4
|
5181
|
|
2
|
32,5
|
100
|
32,6
|
3423
|
|
3
|
33,0
|
120
|
34,0
|
4275
|
Определить среднюю
урожайность пшеницы по трем хозяйствам вместе для каждого года; изменение
средней урожайности в отчетном году по сравнению с предыдущим (в ц/га и %).
Решение
В процессе обработки и
обобщения статистических данных возникает необходимость определения средних
величин. Средняя величина – обобщающая характеристика изучаемого признака в
исследуемой совокупности. Она отражает его типичный уровень в расчете на
единицу совокупности в конкретных условиях места и времени.[1]
Среднюю урожайность
пшеницы по трем хозяйствам для предыдущего года определяем по формуле средней
арифметической взвешенной:
 (5)
(5)
Таким
образом, средняя урожайность пшеницы для предыдущего года
составит:
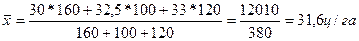
Среднюю урожайность
пшеницы по трем хозяйствам для отчетного года определяем по формуле средней
гармонической взвешенной:
 (6)
(6)
Таким
образом, средняя урожайность пшеницы для отчетного года
составит:
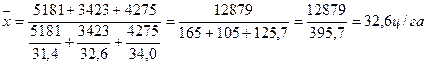
Для анализа изменения
средней урожайности в отчетном году по сравнению с предыдущим составим таблицу
3.
Таблица 3
Изменение средней урожайности
|
Показатель
|
Предыдущий год
|
Отчетный год
|
Изменение
|
|
Абсолютное, ц/га
|
Относительное, %
|
|
Средняя урожайность, ц/га
|
31,6
|
32,6
|
1,0
|
103,2
|
Таким образом, в отчетном
году по сравнению с предыдущим средняя урожайность пшеницы по трем хозяйствам увеличилась
на 1 ц/га, или на 3,2%.
Задача 24
При 10 %-ном бесповторном
отборе рабочих получены следующие данные о тарифных разрядах:
|
Тарифный разряд
|
1
|
2
|
3
|
4
|
5
|
6
|
|
Количество рабочих, чел.
|
8
|
30
|
85
|
105
|
50
|
22
|
Определить с вероятностью
0,997 возможные пределы среднего тарифного разряда рабочих.
Решение
При бесповторном отборе
каждая отобранная единица не возвращается обратно, и вероятность попадания
отдельных единиц в выборку все время изменяется.[2]
Средняя ошибка выборочной
средней определяется по следующей формуле:
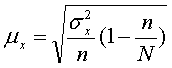 (7)
(7)
где n – численность выборки, n = 300 чел.;
N – численность генеральной
совокупности, N = 3000 (так как отбор составляет 10%).
Дисперсия признака х определяется по формуле:
 (8)
(8)
Среднее выборочное
значение определяется по формуле:
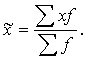 (9)
(9)
Для удобства расчетов
составим вспомогательную таблицу 4.
Таблица 4
|
Тарифный разряд
х
|
Количество рабочих f
|
xf
|
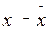
|
(х-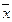 )2* f )2* f
|
|
1
|
8
|
8
|
-2,75
|
60,5
|
|
2
|
30
|
60
|
-1,75
|
61,25
|
|
3
|
85
|
255
|
-0,75
|
47,81
|
|
4
|
105
|
420
|
+0,25
|
6,56
|
|
5
|
50
|
250
|
+1,25
|
78,12
|
|
6
|
22
|
132
|
+2,25
|
111,38
|
|
Итого:
|
300
|
1125
|
─
|
365,62
|
Средний тарифный разряд рабочих составит:
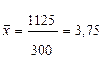
Дисперсия тарифного разряда рабочих составит:

Средняя ошибка тарифного
разряда в выборке составит:

Предельное значение
ошибки выборочной доли определяется по следующей формуле:
 (10)
(10)
Значению вероятности
0,997 соответствует значение гарантийного коэффициента, равное 3. Тогда
предельная ошибка выборочной средней составит:
Δw = 0,00369*3 = 0,011
Средняя величина
количественного признака в генеральной совокупности определяется с учетом
предельной ошибки выборочной средней:
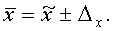 (11)
(11)
 = 3,75±0,011
= 3,75±0,011
Пределы, в которых
находится средний тарифный разряд:
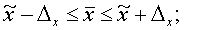
Средний тарифный разряд
находится в пределах 3,74≤ ≤3,76
с вероятностью 0,997.
≤3,76
с вероятностью 0,997.
Задача 34
Имеются данные о
товарообороте, млн. руб.
|
Год
|
|
1
|
2
|
3
|
4
|
5
|
|
900
|
980
|
985
|
990
|
1010
|
По приведенным данным
определить:
1. Абсолютный прирост
(цепной и базисный).
2. Темп роста (цепной и
базисный).
3. Средний уровень ряда.
4. Средний абсолютный
прирост.
5. Средний темп роста.
Решение
Ряд расположенных в
хронологической последовательности значений статистических показателей,
представляет собой временной (динамический) ряд.[3]
Абсолютный прирост, темп
роста, средний уровень ряда, средний абсолютный прирост и средний темп роста
являются статистическими характеристиками ряда динамики.
Определение
статистических характеристик динамического ряда основано на абсолютном и
относительном сравнении уровней ряда (у2
- у1 – абсолютное сравнение, у2/у1
– относительное сравнение).
При
нахождении характеристик могут использоваться два способа:
•
цепной способ, т.е. когда данный уровень сравнивается с предыдущим;
•
базисный способ, т.е. когда каждый данный уровень сравнивается с одним и тем же
начальным уровнем, принятым за базу сравнения.
1. Абсолютный прирост ( ) – это абсолютная разность между последующим и предыдущим уровнями
ряда (цепные) или начальным уровнем ряда (базисные). Цепной абсолютный прирост
характеризует последовательное изменение уровней ряда, а базисный абсолютный
прирост – изменение нарастающим итогом. [4]
) – это абсолютная разность между последующим и предыдущим уровнями
ряда (цепные) или начальным уровнем ряда (базисные). Цепной абсолютный прирост
характеризует последовательное изменение уровней ряда, а базисный абсолютный
прирост – изменение нарастающим итогом. [4]
Абсолютный прирост
показывает, на сколько абсолютных единиц изменился данный уровень по сравнению:
а) с
предыдущим уровнем при цепном способе:
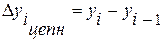 (12)
(12)
где
уi – i-ый уровень ряда,
уi – 1 – i-1-ый уровень ряда.
б) с начальным уровнем при базисном
способе:
 (13)
(13)
где
уi – i-ый уровень ряда,
у1 – начальный, базисный
уровень ряда.
2. Темп роста (Тр)
– это соотношение последующего уровня ряда к предыдущему (цепные темпы роста)
или постоянному, принятому за базу сравнения (базисные темпы роста):
Цепные коэффициенты (темпы) роста рассчитываются по
формуле:
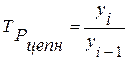 (14)
(14)
Базисные коэффициенты (темпы) роста рассчитываются по
формуле:
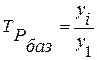 , (15)
, (15)
Темп роста может
выражаться в коэффициентах или в процентах.
Так
как показатели в течение рассматриваемого периода времени изменяются,
изменяются и характеристики ряда. Поэтому, чтобы получить общее представление об
изменении данных показателей, следует найти обобщающие характеристики, т.е.
средние величины.
3. Средний уровень ряда ( )
характеризует среднюю величину показателя за данный период. Средний уровень
ряда рассчитывается как среднее арифметическое из уровней этого ряда:
)
характеризует среднюю величину показателя за данный период. Средний уровень
ряда рассчитывается как среднее арифметическое из уровней этого ряда:
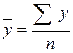 (16)
(16)
где n-1 – количество изменений за данный период.
4.
Средний абсолютный прирост ( ) – это средняя из абсолютных приростов за равные промежутки
времени:
) – это средняя из абсолютных приростов за равные промежутки
времени:
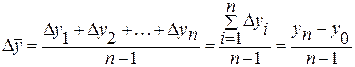 , (17)
, (17)
где
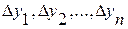 – соответствующий
абсолютный прирост,
– соответствующий
абсолютный прирост,
n-1 –
количество изменений за данный период,
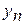 – последний уровень
ряда,
– последний уровень
ряда,
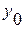 – начальный, базисный
уровень ряда.
– начальный, базисный
уровень ряда.
5. Средний темп роста (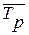 ) − это средняя
из темпов роста за данный период, которая показывает, во сколько раз в среднем
(за год, месяц) изменяется явление.
) − это средняя
из темпов роста за данный период, которая показывает, во сколько раз в среднем
(за год, месяц) изменяется явление.
Средний темп роста можно определить исходя из цепных
коэффициентов (темпов) роста:
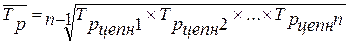 , (18)
, (18)
или абсолютных уровней ряда (базисного темпа роста):
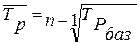 , (19)
, (19)
где 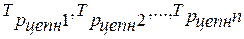 ─
соответствующие цепные темпы роста (yi / yi-1),
─
соответствующие цепные темпы роста (yi / yi-1),
 ─ базисный
темп роста за весь период (yn / y0).
─ базисный
темп роста за весь период (yn / y0).
Результаты расчетов занесем в таблицу 5.
Таблица 5
Расчет аналитических
показателей ряда динамики
|
Показатель
|
год
|
|
1(баз.)
|
2
|
3
|
4
|
5
|
|
Товарооборот, млн. руб.
|
900
|
980
|
985
|
990
|
1010
|
|
Абсолютный прирост, млн. руб.
─ базисный
─ цепной
|
─
─
|
80
80
|
85
5
|
90
5
|
110
20
|
|
Темп роста
─ базисный
─ цепной
|
─
─
|
1,089
1,089
|
1,094
1,005
|
1,1
1,005
|
1,12
1,02
|
|
Средний уровень ряда, млн. руб.
|
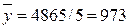
|
|
Средний
абсолютный прирост, %
|
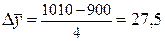
|
|
Средний темп роста
|
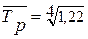 = 1,051, или 105,1 % = 1,051, или 105,1 %
|
По результатам расчета
можно сделать следующие выводы:
Рассчитанные
аналитические коэффициенты характеризуют состояние товарооборота фирмы за 5
лет. Абсолютный прирост выражает абсолютную скорость роста товарооборота, по
сравнению с первым годом она составила 110 млн. рублей. Темп роста показывает,
что товарооборот пятого года составляет 112 % от уровня базисного года. Средний
ежегодный товарооборот составил 973 млн. рублей, при этом товарооборот
увеличивался в среднем на 5,1%. Средний абсолютный прирост составил 27,5 млн.
рублей.
Задача 44
По приведенным ниже
данным определить:
1. Индекс цен переменного
состава.
2. Индекс цен постоянного
состава.
3. Индекс влияния
структурных сдвигов.
Данные о производстве и
себестоимости продукции по трем предприятиям:
|
Предприятие
|
Производство продукции, тыс.шт.
|
Цена единицы продукции, тыс. р.
|
|
Базисный период
|
Отчетный период
|
Базисный период
|
Отчетный период
|
|
1
|
140
|
145
|
40
|
45
|
|
2
|
200
|
220
|
42
|
46
|
|
3
|
400
|
430
|
35
|
40
|
Решение
Индекс
переменного состава представляет отношение среднего уровня явления в отчетном
периоде к его среднему значению в базисном периоде.[5]
 ↑12,5%
↑12,5%
Индекс постоянного
(фиксированного) состава исключает влияние изменения структуры (состава)
совокупности на динамику средних величин, рассчитанных для двух периодов при
одной и той же фиксированной структуре.
 ↑12%
↑12%
Индекс
влияния структурных сдвигов используют для определения изменения обобщающей
средней под влиянием изменения структуры совокупности.
Индекс
влияния структурных сдвигов определяется как отношение индекса переменного
состава к индексу постоянного состава.
Icc = 1,125/1,12=1,004
Поскольку
индекс цен переменного
состава равен 1,125, или 112,5%, то средняя цена единицы продукции по трем
предприятиям увеличилась на 12,5%. Индекс цен постоянного состава равен 1,12, или 112%, значит,
средняя цена единицы продукции по трем предприятиям увеличилась на 12%. Индекс
структурных сдвигов равен 1,004, значит, средняя цена единицы продукции по трем
предприятиям увеличилась на 0,4% за счет изменения структуры.
СПИСОК ЛИТЕРАТУРЫ
1. Гусаров В.М. Теория
статистики. – М.: ЮНИТИ, 1998. – 448 с.
2. Елисеева И.И., Юзбашев
М.М. Общая теория статистики. – М.: Финансы и статистика, 1998. – 368 с.
3. Ефимова М. Р., Петрова
Е.В., Румянцев В.Н. Общая теория статистики. – М.: ИНФРА-М. 2002. – 416 с.
4. Савицкая Г. В. Анализ
хозяйственной деятельности предприятия. 2-е изд., испр. и доп. – М.: ИНФРА-М.
2003. − 400 с.
5. Теория статистики /
Под редакцией Шмойловой Р. А. – М.: Финансы и статистика, 2002. – 576 с.
[1] Ефимова М. Р., Петрова Е.В., Румянцев В.Н. Общая теория
статистики. – М.: ИНФРА-М. 2002. – с. 89
[2] Гусаров В.М. Теория статистики. – М.: ЮНИТИ, 1998. – с.
161
[3] Елисеева И.И., Юзбашев М.М. Общая теория статистики.
– М.: Финансы и статистика, 1998. – с. 281
[4] Теория статистики / Под редакцией Шмойловой Р. А. –
М.: Финансы и статистика, 2002. – с. 189
[5] Ефимова М. Р., Петрова Е.В., Румянцев В.Н. Общая
теория статистики. – М.: ИНФРА-М. 2002. – с. 370