1. Найти неопределенный интеграл:

Решение:

2. Вычислить определенные интегралы:

Решение:

3. Вычислить определенные интегралы:

4. Решить дифференциальное уравнение:

Решение:

Линейное неоднородное уравнение. Решим методом Бернулли:

5. Вычислить площадь фигуры, ограниченой линиями:

Решение:

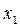
	-1	0	1	2	3	4
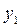
	-4,9	-2,1	0,9	4,1	7,1	9,9

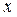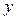6. Экспериментальные данные о значениях переменных  и приведены в таблице:

В результате их выравнивания получена функция 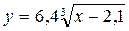.Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью 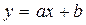 (найти параметры 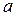и 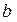). Выяснить, какая из двух линей лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.

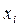
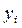
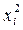
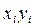
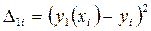
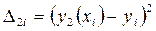
	-1	-4,9	1	4,9	12,96	0,0064
	0	-2,1	0	0	0	0,0121
	1	0,9	1	0,9	11,56	0,01
	2	4,1	4	8,2	3,4726	0,0121
	3	7,1	9	21,3	0,0009	0,0144
	4	9,9	16	39,6	3,3879	0,0049
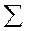
	9	15	31	74,9	14,3449	0,0599

 

 

 

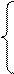
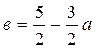
Поскольку 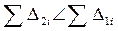, то вторая линия 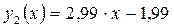лучше данную.

7. Исследовать сходимость численного ряда. В случае сходимости ряда установите её характер (абсолютная или условная):

Решение:

Это знакочередующий ряд.

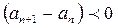, значит общий член монотонно убывает по модулю.

По признаку Лейбница ряд сходится.

Иследуем ряд 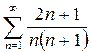            Сравним его с рядом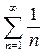

Ряд 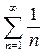расходится, значит по признаку сравнения 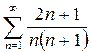также расходится.

ВЫВОД: 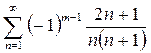сходится условно.