Лабораторная работа № 1
Задание
1. Для его выполнения необходимо
использовать кванторы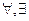 
и операции
математической логики: 
и перевести предложения с русского на язык предикатов.
Все суть S или
P.
Нет никакого х, такого,
что А(х).
Решение:
Все суть S или
P: 
Нет никакого х, такого,
что А(х) 
Эх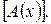 
Задание 2. Для выполнения необходимо из системы
продукции выбрать цель, т.е. одно утверждение, стоящее в правой части, и построить цепочки вывода
для прямой и обратной цепочек рассуждений.
База данных: А,С, D, E, G, H, K, L, M, J.
Цель прямой цепочки: В.
Цель обратной цепочки: F.
База правил: 
Решение:
Прямая цепочка вывода:
С
D
Е B.
L G
F
K
L I
H
M
Обратная цепочка вывода:
G
F.
L G
ЛАБОРАТОРНАЯ РАБОТА № 2
Задание 1. Для его
выполнения необходимо в тексте выделить простые предложения, обозначив их как
атомы и затем представить каждое утверждение в виде формулы. Далее доказать
теорему, основанную на резолюции путем построения противоречия или
опровержения.
Вариант задания: Шар 2
находится всегда в том месте, где находится шар 1. Шар 3 находится в месте А.
Если шар 3 находится в месте А, то шар 1 находится в месте В. Где находится шар
2?
Решение:
1. 
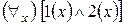
2. 
3. Э(х) 
Необходимо доказать:
4. Э(х)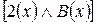 
Преобразуем:
1. 
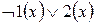
2. 
3. а) 1(с);
б) В (с), с – константа.
Отрицание теоремы,
которую надо доказать:
4. 
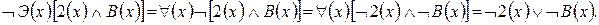
Мы получили пустой
дизъюнкт 
четвёртое утверждение доказано.
Задание 2. Нечеткие
выводы.
ЗДЕСЬ НЕТ ПОСТАНОВКИ ЗАДАЧИ, ЕСТЬ ТОЛЬКО КАКОЙ-ТО РАЗОБРАННЫЙ
ПРИМЕР
Пусть U и Y –
это области натуральных чисел от 1 до 4, тогда
нечеткое множество 
Кроме того, пусть F’= около 4 (В примере F’= около 2 =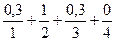
)
При условиях: «Если U маленькое, то V большое», определить
«что есть V»
В примере
Определяется вывод 
Ответ «V
есть G», где 