ГОУ ВПО Всероссийский заочный финансово
– экономический институт.
Серпуховское представительство
Факультет:
финансово – кредитный
Кафедра: Высшей математики
Контрольная работа № 1
Дисциплина: Математический анализ и линейная алгебра
Тема:
Вариант №1
Исполнитель: Н.В. Кузьмина
Специальность: финансы и
кредит.
Группа: № 153
№ зачетной книжки: № 05 ФФД 70071
Руководитель: Доц. к.ф.-м.н.
Борисова В.И.
СЕРПУХОВ 2006 г.
1. Методом Гаусса
решить систему уравнений:

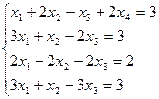

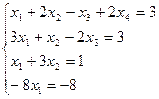

Ответ: 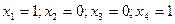
2. Найти предел 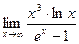
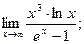
Пусть 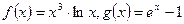
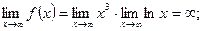

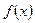 и
и  непрерывны при
непрерывны при  , тогда по правилу Лопиталя (применяя его несколько раз),
получим:
, тогда по правилу Лопиталя (применяя его несколько раз),
получим:
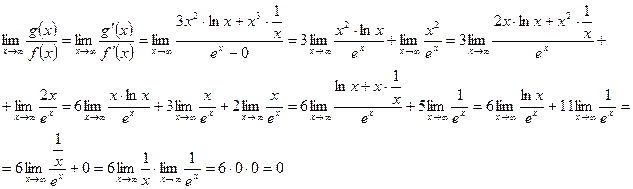 Ответ:
Ответ: 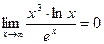
3. Найти производную функции: 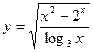
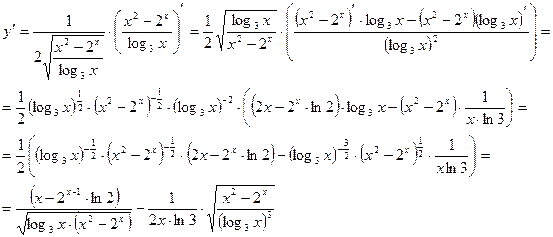
Ответ: 
4. Среди равнобедренных треугольников с
боковой стороной 5 см. Найти длину основания треугольника с наибольшей
площадью.
 Пусть ABC-
равнобедренный треугольник.
Пусть ABC-
равнобедренный треугольник.
Расположим
оси координатной плоскости
X0Y так, чтобы ось 0X проходила через основание AC, а ось 0Y- через
высоту, опущенную на основание. Пусть координаты точек : C(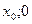 ), B(
), B(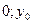 ), тогда A(
), тогда A( ). По условию BC=5см., то есть
). По условию BC=5см., то есть 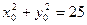 , значит
, значит
 .
.
Площадь
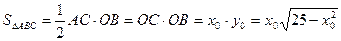 .
.
Пусть
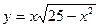 . Функция достигает максимума, если
. Функция достигает максимума, если 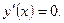

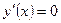 при
при 
Из
условия  , значит
, значит 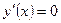 при
при 
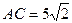 (см)
(см)
Ответ:  см.
см.
5. Написать уравнение прямой, проходящей
через точку (1;2) параллельно касательной к графику функции  , проведённой в точке
с абсциссой
, проведённой в точке
с абсциссой  , сделать чертеж.
, сделать чертеж.
Производная
функции 
 равна:
равна:
 а уравнение
касательной в точке
а уравнение
касательной в точке  , как известно,
, как известно,
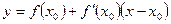 , то есть
, то есть
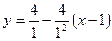 или
или

Так
как искомая прямая параллельна этой касательной, ее уравнение будет иметь вид:
 .
.
Константу
b
найдем, подставляя координаты точки (1;2), через которую проходит искомая
прямая:
 , отсюда
, отсюда  , а уравнение
прямой
, а уравнение
прямой 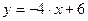 .
.
Ответ: 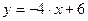
6. Исследовать функцию и построить
график.

1. Область определения функции:

2. Функция непрерывна на всей области определения.
3. При 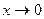
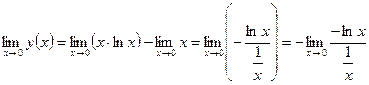
Пусть 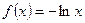 ;
; 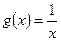
По
правилу Лопиталя
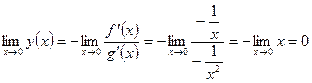 .
.
То есть,
при 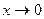

4. Функция не является ни четной, ни нечетной
5. Найдем точки пересечения графиком оси 0X:
y=0:  x>0
x>0  lnx=1; x=e;
lnx=1; x=e;
Точка пересечения оси 0X имеет координаты 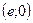 .
.
6. При 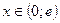 y<0; при
y<0; при  y>0.
y>0.
7. 
Производная обращается в нуль при x=1; в
интервале  она отрицательна, в
интервале
она отрицательна, в
интервале  она положительна.
она положительна.
Значит, при  функция убывает, при
функция убывает, при  возрастает, в точке x=1 имеет
минимум
возрастает, в точке x=1 имеет
минимум 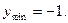
8.
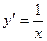
Вторая производная не имеет нулей и при 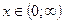 положительна, значит,
график функции вогнутый.
положительна, значит,
график функции вогнутый.
9.
При 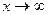
 Так как при
Так как при 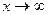
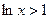 , то
, то 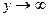 .
.
Найдем наклонную асимптоту:
 , то есть график не имеет наклонной асимптоты.
, то есть график не имеет наклонной асимптоты.
Список используемой
литературы
1. Высшая математика для экономистов: Учебник для
вузов/ Н.Ш.Кремер, Б.А.Путко, И.М. Тришин, М.Н. Фридман; Под ред. проф. Н.Ш.Кремера.
– 2-е изд., перераб. И доп. – М.: банки и биржи, ЮНИТИ, 1998.