ЗАДАЧА 1
По предприятиям легкой
промышленности региона получена информация, характеризующая зависимость объема
выпускаемой продукции (Y, млн. руб.) от объема капиталовложений (X, млн.
руб.):
|
№ предприятия
|
X
|
Y
|
|
1
|
12
|
21
|
|
2
|
4
|
10
|
|
3
|
18
|
26
|
|
4
|
27
|
33
|
|
5
|
26
|
34
|
|
6
|
29
|
37
|
|
7
|
1
|
9
|
|
8
|
13
|
21
|
|
9
|
26
|
32
|
|
10
|
5
|
14
|
Требуется:
1. Найти параметры уравнения линейной регрессии, дать
экономическую интерпретацию углового коэффициента регрессии.
2. Вычислить остатки; найти остаточную сумму квадратов; определить
стандартную ошибку регрессии; построить график остатков.
3. Проверить выполнение предпосылок метода наименьших
квадратов.
4. Осуществить проверку значимости параметров уравнения
регрессии с помощью t-критерия Стьюдента (уровень значимости a=0,05).
5. Вычислить коэффициент детерминации R2; проверить значимость уравнения регрессии с помощью F-критерия
Фишера (уровень значимости a=0,05); найти среднюю относительную ошибку
аппроксимации. Сделать вывод о качестве модели.
6. Осуществить прогнозирование значения показателя Y при уровне
значимости a=0,1, если прогнозное значения фактора Х составит 80 % от его максимального
значения.
7. Представить графически: фактические и модельные
значения Y, точки прогноза.
8. Составить уравнения нелинейной регрессии:
Ø логарифмической;
Ø степенной;
Ø показательной.
Привести графики построенных уравнений
регрессии.
9. Для указанных моделей найти коэффициенты детерминации
и средние относительные ошибки аппроксимации.
Сравнить модели по этим характеристикам и сделать вывод.
РЕШЕНИЕ
Для решения задачи используется
табличный процессор EXCEL.
1. С помощью надстройки «Анализ данных» EXCEL проводим
регрессионный анализ и определяем параметры уравнения линейной регрессии  (меню «Сервис»
® «Анализ данных…» ® «Регрессия»):
(меню «Сервис»
® «Анализ данных…» ® «Регрессия»):

(Для копирования снимка окна в буфер обмена
данных WINDOWS используется комбинация клавиш Alt+Print Screen.)
В результате этого уравнение регрессии
будет иметь вид:
 (прил. 1).
(прил. 1).
Угловой
коэффициент b1=0,968 является по
своей сути средним абсолютным приростом.
Его значение показывает, что при
увеличении объема капиталовложений X на 1 млн. руб. объем выпускаемой продукции Y возрастает в среднем на 0,968 млн. руб.
2. При проведении регрессионного
анализа в EXCEL одновременно были определены
остатки регрессии  (i=1, 2, …, n,
где n=10 — число наблюдений значений переменных X и Y) (см. «Вывод остатка» в прил. 1) и рассчитана остаточная
сумма квадратов
(i=1, 2, …, n,
где n=10 — число наблюдений значений переменных X и Y) (см. «Вывод остатка» в прил. 1) и рассчитана остаточная
сумма квадратов

(см.
«Дисперсионный анализ» в прил.
1).
Стандартная ошибка линейной парной регрессии
Sрег определена там же:
 млн. руб.
млн. руб.
(см.
«Регрессионную статистику» в прил.
1), где p=1 — число факторов в регрессионной модели.
График остатков ei от предсказанных уравнением
регрессии значений результата 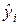 (i=1, 2, …, n) строим с помощью диаграммы EXCEL. Предварительно в «Выводе остатка» прил. 1 выделяются блоки ячеек
«Предсказанное Y» и «Остатки»
вместе с заголовками, а затем выбирается пункт меню «Вставка» ® «Диаграмма…»
® «Точечная»:
(i=1, 2, …, n) строим с помощью диаграммы EXCEL. Предварительно в «Выводе остатка» прил. 1 выделяются блоки ячеек
«Предсказанное Y» и «Остатки»
вместе с заголовками, а затем выбирается пункт меню «Вставка» ® «Диаграмма…»
® «Точечная»:
График остатков приведен в прил. 2.
3. Проверим
выполнение предпосылок обычного метода наименьших квадратов.
1) Случайный характер остатков.
Визуальный анализ графика остатков не
выявляет в них какой-либо явной закономерности.
Проверим
исходные данные на наличие аномальных наблюдений объема выпускаемой продукции Y (выбросов). С этой целю сравним абсолютные
величины стандартизированных остатков
(см. «Вывод остатка» в прил. 1) с табличным значением t-критерия Стьюдента для уровня значимости a=0,05 и числа степеней свободы остатка
регрессии 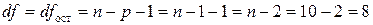 , которое составляет tтаб=2,306.
, которое составляет tтаб=2,306.
Видно,
что ни один из стандартизированных остатков не превышает по абсолютной величине табличное значение t-критерия Стьюдента. Это свидетельствует об отсутствии выбросов.
2) Нулевая средняя величина остатков. Данная
предпосылка всегда выполняется для линейных моделей со свободным коэффициентом b0, параметры которых оцениваются обычным методом
наименьших квадратов. В нашей модели алгебраическая сумма остатков и,
следовательно, их среднее, равны нулю:  (см. прил.
1).
(см. прил.
1).
Для
вычисления суммы и среднего значений остатков использовались встроенные функции
EXCEL «СУММ» и «СРЗНАЧ».
3) Одинаковая дисперсия (гомоскедастичность) остатков. Выполнение
данной предпосылки проверим методом Глейзера в предположении линейной
зависимости среднего квадратического отклонения возмущений  от предсказанных уравнением регрессии значений
результата
от предсказанных уравнением регрессии значений
результата 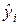 (i=1, 2, …, n). Для этого рассчитывается
коэффициент корреляции
(i=1, 2, …, n). Для этого рассчитывается
коэффициент корреляции  между абсолютными
величинами остатков
между абсолютными
величинами остатков  и
и 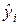 (i=1, 2, …, n) с помощью выражения,
составленного из встроенных функций:
(i=1, 2, …, n) с помощью выражения,
составленного из встроенных функций:
=КОРРЕЛ(ABS(«Остатки»);«Предсказанное Y»)
Коэффициент
корреляции оказался равным 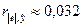 (см. прил.
1).
(см. прил.
1).
Критическое
значение коэффициента корреляции для уровня значимости a=0,05 и числа степеней свободы 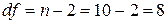 составляет rкр=0,632.
составляет rкр=0,632.
Так
как коэффициент корреляции  не превышает по абсолютной величине
критическое значение, то
статистическая гипотеза об одинаковой дисперсии остатков не отклоняется на
уровне значимости a=0,05.
не превышает по абсолютной величине
критическое значение, то
статистическая гипотеза об одинаковой дисперсии остатков не отклоняется на
уровне значимости a=0,05.
4) Отсутствие
автокорреляции в остатках. Выполнение
данной предпосылки проверяем методом Дарбина–Уотсона. Предварительно ряд
остатков упорядочивается в зависимости от последовательно возрастающих значений
результата Y, предсказанных уравнением регрессии. Для этой цели в
«Выводе остатка» прил. 1 выделяется любая
ячейка в столбце «Предсказанное
Y», и
на панели инструментов нажимается кнопка « » («Сортировка по возрастанию»). По
упорядоченному ряду остатков рассчитываем d‑статистику Дарбина–Уотсона
» («Сортировка по возрастанию»). По
упорядоченному ряду остатков рассчитываем d‑статистику Дарбина–Уотсона
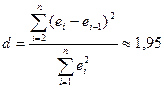 (см. прил.
1).
(см. прил.
1).
Для
расчета d‑статистики
использовалось выражение,
составленное из встроенных функций EXCEL:
=СУММКВРАЗН(«Остатки 2, …, n»; «Остатки 1, …, n–1»)/СУММКВ(«Остатки 1, …,n»)
Критические
значения d‑статистики для числа
наблюдений n=10, числа факторов p=1 и уровня значимости a=0,05 составляют: d1=0,88; d2=1,32.
Так
как выполняется условие
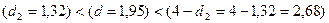 ,
,
статистическая гипотеза об отсутствии
автокорреляции в остатках не отклоняется на уровне значимости a=0,05.
Проверим
отсутствие автокорреляции в остатках также и по коэффициенту автокорреляции
остатков первого порядка
 (см. прил.
1).
(см. прил.
1).
(ряд остатков упорядочен в той же самой
последовательности).
Для
расчета коэффициента автокорреляции использовалось выражение, составленное из встроенных функций:
=СУММПРОИЗВ(«Остатки 2, …, n»; «Остатки 1, …, n–1»)/СУММКВ(«Остатки 1, …,n»)
Критическое
значение коэффициента автокорреляции для числа наблюдений n=10 и уровня
значимости a=0,05
составляет r(1)кр=0,632. Так как коэффициент
автокорреляции остатков первого порядка не превышает по абсолютной величине
критическое значение, то это еще раз указывает на отсутствие автокорреляции в
остатках.
5) Нормальный закон распределения
остатков. Выполнение этой предпосылки
проверяем с помощью R/S-критерия, определяемого по формуле
 ,
,
где emax=1,27;
emin=(–1,99)
— наибольший и наименьший остатки соответственно (определялись с помощью
встроенных функций «МАКС» и «МИН»);  — стандартное
отклонение ряда остатков (определено с помощью встроенной функции «СТАНДОТКЛОН») (см. прил.
1).
— стандартное
отклонение ряда остатков (определено с помощью встроенной функции «СТАНДОТКЛОН») (см. прил.
1).
Критические границы R/S-критерия для числа
наблюдений n=10 и уровня значимости a=0,05 имеют значения: (R/S)1=2,67 и (R/S)2=3,69.
Так как расчетное значение R/S-критерия попадает в интервал между критическими границами,
то статистическая гипотеза о нормальном
законе распределения остатков не отклоняется на уровне
значимости a=0,05.
Проведенная
проверка показала, что выполняются все пять предпосылок обычного метода
наименьших квадратов. Это свидетельствует об адекватности регрессионной модели
исследуемому экономическому явлению.
4. Проверим
статистическую значимость коэффициентов b0 и b1 уравнения
регрессии. Табличное значение t-критерия Стьюдента для уровня значимости a=0,05 и числа степеней свободы остатка линейной парной
регрессии  составляет tтаб=2,306.
составляет tтаб=2,306.
t-статистики
коэффициентов
 ,
,
были определены при проведении регрессионного анализа
в EXCEL и имеют следующие
значения: tb0»11,41; tb1»25,81 (см. прил. 1). Анализ
этих значений показывает, что по абсолютной величине все они превышают табличное
значение t-критерия Стьюдента. Это свидетельствует о
статистической значимости обоих коэффициентов. На то же самое обстоятельство
указывают и вероятности случайного формирования коэффициентов b0 и b1, которые
ниже допустимого уровня значимости a=0,05 (см. «P‑Значение»).
Статистическая
значимость углового коэффициента b1 дает
основание говорить о существенном (значимом) влиянии изменения объема
капиталовложений X на изменение объема выпускаемой продукции Y.
5. Коэффициент
детерминации R2 линейной модели также был определен при проведении
регрессионного анализа в EXCEL:

(см. «Регрессионную
статистику» в прил. 1).
Значение R2
показывает, что линейная модель объясняет 99 % вариации объема выпускаемой
продукции Y.
F-статистика линейной модели имеет значение

(см. «Дисперсионный
анализ» в прил. 1).
Табличное
значение F-критерия Фишера для уровня значимости a=0,05 и чисел степеней свободы числителя (регрессии)  и знаменателя (остатка)
и знаменателя (остатка)
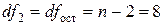 составляет Fтаб=5,32. Так
как F-статистика превышает табличное значение F-критерия Фишера, то это свидетельствует о статистической
значимости уравнения регрессии в целом. На этот же факт указывает и то, что
вероятность случайного формирования уравнения регрессии в том виде, в каком оно
получено, составляет 5,45×10-9 (см. «Значимость F» в «Дисперсионном анализе» прил. 1), что ниже допустимого
уровня значимости a=0,05.
составляет Fтаб=5,32. Так
как F-статистика превышает табличное значение F-критерия Фишера, то это свидетельствует о статистической
значимости уравнения регрессии в целом. На этот же факт указывает и то, что
вероятность случайного формирования уравнения регрессии в том виде, в каком оно
получено, составляет 5,45×10-9 (см. «Значимость F» в «Дисперсионном анализе» прил. 1), что ниже допустимого
уровня значимости a=0,05.
Среднюю относительную ошибку аппроксимации определяем по приближенной
формуле
 ,
,
где  млн. руб. — средний
объем выпускаемой продукции, определенный с помощью встроенной функции «СРЗНАЧ» (см. «Исходные данные» в прил. 1).
млн. руб. — средний
объем выпускаемой продукции, определенный с помощью встроенной функции «СРЗНАЧ» (см. «Исходные данные» в прил. 1).
Значение Еотн
показывает, что предсказанные уравнением регрессии значения объема выпускаемой
продукции Y отличаются от фактических значений в среднем на 4,0 %.
Линейная модель имеет хорошую точность.
По
результатам проверок, проведенных в пунктах 3 — 5, можно сделать вывод о
достаточно хорошем качестве линейной модели и возможности ее использования для
целей анализа и прогнозирования объема выпускаемой продукции.
6. Спрогнозируем объем выпускаемой продукции Y, если прогнозное значение объема капиталовложений X составит 80 % от своего максимального значения в исходных данных:
§ максимальное значение X — xmax=29 млн.
руб. (см. «Исходные данные» в прил.
1);
§ прогнозное значение X —  млн. руб.
млн. руб.
Среднее
прогнозируемое значение объема выпускаемой продукции
(точечный прогноз) равно
 млн. руб.
млн. руб.
Стандартная
ошибка прогноза фактического значения объема выпускаемой продукции y0 рассчитывается по формуле
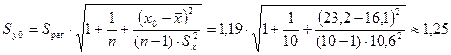 млн. руб.,
млн. руб.,
где  млн. руб. — средний
объем капиталовложений;
млн. руб. — средний
объем капиталовложений;  млн. руб. —
стандартное отклонение объема капиталовложений (определены с помощью встроенных
функций «СРЗНАЧ» и «СТАНДОТКЛОН») (см. «Исходные данные» в прил. 1).
млн. руб. —
стандартное отклонение объема капиталовложений (определены с помощью встроенных
функций «СРЗНАЧ» и «СТАНДОТКЛОН») (см. «Исходные данные» в прил. 1).
Интервальный прогноз фактического
значения объема выпускаемой продукции y0 с
надежностью (доверительной вероятностью) g=0,9 (уровень значимости
a=0,1) имеет вид:
 млн. руб.,
млн. руб.,
где
tтаб=1,860 — табличное значение t-критерия Стьюдента при уровне значимости a=0,1
и числе степеней свободы  .
.
Таким
образом, объем выпускаемой продукции Y с
вероятностью 90 % будет находиться в интервале от 28,25 до 32,91 млн. руб.
7. График, на котором изображены фактические и предсказанные
уравнением регрессии значения Y строим с помощью диаграммы EXCEL (меню «Вставка» ® «Диаграмма…»
® «Точечная»). Далее строим линию линейного
тренда (меню «Диаграмма» ® «Добавить
линию тренда…» ® «Линейная»), и устанавливаем
вывод на диаграмме уравнения регрессии и коэффициента детерминации R2:


Точки точечного и интервального прогнозов
наносим на график вручную (прил. 3).
8. Логарифмическую, степенную и
показательную модели также строим с помощью диаграммы EXCEL (меню «Вставка»
® «Диаграмма…» ® «Точечная»).
Далее последовательно строим соответствующие линии тренда (меню «Диаграмма» ® «Добавить
линию тренда…»), и устанавливаем вывод на диаграмме уравнения регрессии и
коэффициента детерминации R2:


Графики линий регрессии, уравнения
регрессии и значения R2 приведены в прил. 4. Рассмотрим последовательно
каждую модель.
1)
Логарифмическая модель:
 .
.
Значение параметра b1=8,6672
показывает, что при увеличении объема капиталовложений X на 1 % объем выпускаемой продукции
Y возрастает в среднем на 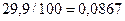 млн. руб.
млн. руб.
Коэффициент
детерминации R2»0,8562 показывает, что логарифмическая модель
объясняет 85,62 % вариации объема выпускаемой продукции Y.
F-статистика
Фишера логарифмической модели определяется через коэффициент детерминации R2 по формуле
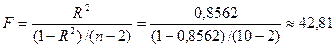 .
.
Табличное
значение F-критерия Фишера одинаково как для линейной, так и для
всех нелинейных моделей, которые здесь строятся (Fтаб=5,32).
Так как F-статистика превышает табличное значение F-критерия, то это свидетельствует о статистической
значимости уравнения логарифмической регрессии.
Стандартная ошибка логарифмической
регрессии также рассчитывается через коэффициент детерминации R2 по формуле
 млн. руб.,
млн. руб.,
где  млн. руб. —
стандартное отклонение объема выпускаемой продукции, определенное с помощью
встроенной функции «СТАНДОТКЛОН» (см.
«Исходные данные» в прил.
1).
млн. руб. —
стандартное отклонение объема выпускаемой продукции, определенное с помощью
встроенной функции «СТАНДОТКЛОН» (см.
«Исходные данные» в прил.
1).
Среднюю относительную ошибку аппроксимации определяем по приближенной
формуле
 .
.
Предсказанные уравнением логарифмической регрессии
значения объема выпускаемой продукции Y отличаются от фактических значений в среднем на 13,97
%. Логарифмическая модель имеет хорошую точность.
2) Степенная модель:
 .
.
Показатель степени b1=0,4531 является средним коэффициентом эластичности. Его
значение показывает, что при увеличении объема капиталовложений X на 1 % объем выпускаемой продукции
Y возрастает в среднем на 0,4531 %.
Коэффициент
детерминации R2»0,9277 показывает, что степенная модель объясняет 92,77
% вариации объема выпускаемой продукции Y.
F-статистика
степенной модели

также превышает табличное значение F-критерия Фишера (Fтаб=5,32),
что указывает на статистическую значимость уравнения степенной регрессии.
Стандартная ошибка степенной регрессии
равна
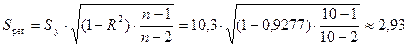 млн. руб.
млн. руб.
Средняя относительная ошибка аппроксимации имеет значение
 .
.
Предсказанные уравнением степенной регрессии значения
объема выпускаемой продукции Y отличаются от фактических значений в среднем на 9,92
%. Степенная модель имеет хорошую точность.
3) Показательная (экспоненциальная)
модель:
 ,
,
где
е=2,718… — основание натуральных логарифмов;  — функция экспоненты
(в EXCEL встроенная функция «EXP»).
— функция экспоненты
(в EXCEL встроенная функция «EXP»).
Параметр b1=1,0474 является средним коэффициентом роста. Его значение показывает, что при
увеличении объема капиталовложений X на 1 млн. руб. объем выпускаемой продукции Y возрастает в
среднем в 1,0474 раза, то есть на 4,7 %.
Коэффициент
детерминации R2»0,9413 показывает, что показательная модель объясняет 94,13
% вариации объема выпускаемой продукции Y.
F-статистика
показательной модели

превышает табличное значение F-критерия Фишера (Fтаб=5,32),
что свидетельствует о статистической значимости уравнения показательной регрессии.
Стандартная ошибка показательной
регрессии:
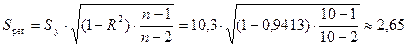 млн. руб.
млн. руб.
Средняя относительная ошибка аппроксимации:
 .
.
Предсказанные уравнением показательной регрессии
значения объема выпускаемой продукции Y отличаются от фактических значений в среднем на 8,95
%. Показательная модель имеет хорошую точность.
Сравнивая
между собой коэффициенты детерминации R2
четырех построенных моделей (линейной, логарифмической, степенной и показательной),
можно придти к выводу, что лучшей моделью является логарифмическая модель, так
как она имеет самое большое значение R2.
ПРИЛОЖЕНИЕ: компьютерные распечатки на 4 листах.
ЗАДАЧА 2
Задача 2а и
2б
Для каждого
варианта даны по две структурные формы модели, которые заданы в виде матриц
коэффициентов модели. Необходимо записать системы одновременных уравнений и
проверить обе системы на идентифицируемость.
|
Номер варианта
|
Номер уравнения
|
Задача 2а
|
Задача 2б
|
|
переменные
|
переменные
|
|
у1
|
у2
|
у3
|
х1
|
х2
|
х3
|
x4
|
у1
|
у2
|
у3
|
х1
|
х2
|
х3
|
x4
|
|
9
|
1
|
-1
|
b12
|
0
|
a11
|
a12
|
a13
|
0
|
-1
|
b12
|
b13
|
a11
|
a12
|
0
|
0
|
|
2
|
0
|
-1
|
b23
|
a21
|
0
|
a23
|
a24
|
b21
|
-1
|
b23
|
0
|
0
|
a23
|
a24
|
|
3
|
0
|
b32
|
-1
|
a31
|
a32
|
a33
|
0
|
b31
|
b32
|
-1
|
0
|
0
|
a33
|
a34
|
РЕШЕНИЕ
Задача
2а
Используя
матрицу коэффициентов модели в
исходных данных, записываем систему одновременных уравнений регрессии в
структурной форме:

Проверим
каждое уравнение системы на выполнение необходимого и достаточного условия
идентификации.
В первом уравнении две эндогенные
переменные: y1 и y2 (H=2). В нем отсутствует
одна экзогенные переменные x2 (D=1). Необходимое условие
идентификации  выполнено. Для проверки на достаточное
условие составим матрицу из коэффициентов при переменных у3 и x4, отсутствующих в данном уравнении, но имеющихся
в системе:
выполнено. Для проверки на достаточное
условие составим матрицу из коэффициентов при переменных у3 и x4, отсутствующих в данном уравнении, но имеющихся
в системе:
|
Уравнения, из которых взяты коэффициенты при переменных
|
Переменные
|
|
у3
|
x4
|
|
2
|
b23
|
a24
|
|
3
|
-1
|
0
|
Определитель
данной матрицы не равен нулю:
 ,
,
а ее ранг равен 2. В заданной системе
уравнений две эндогенные переменные — y1 и y2 . Так как ранг матрицы не меньше, чем
количество эндогенных переменных в системе без одного, то достаточное условие
идентификации для данного уравнения выполнено. Первое уравнение считается идентифицируемым.
Во втором уравнении две эндогенные
переменные: y2 и y3 (H=2). В нем отсутствует одна
экзогенная переменная x2 (D=1). Необходимое условие идентификации
 выполнено. Составим матрицу из
коэффициентов при переменных y1 и x3, которые
отсутствуют во втором уравнении:
выполнено. Составим матрицу из
коэффициентов при переменных y1 и x3, которые
отсутствуют во втором уравнении:
|
Уравнения, из которых взяты коэффициенты при переменных
|
Переменные
|
|
y1
|
x3
|
|
1
|
-1
|
a13
|
|
3
|
0
|
a33
|
Определитель
данной матрицы не равен нулю:
 ,
,
а ее ранг равен 2. Достаточное условие идентификации
выполнено, и второе уравнение считается идентифицируемым.
В третьем уравнении две эндогенные
переменные: y2 и y3
(H=2). В нем отсутствует экзогенные переменные x4 (D=1). Необходимое условие
идентификации  выполнено. Составим матрицу из
коэффициентов при переменных х4 и у1,
которые отсутствуют в третьем уравнении:
выполнено. Составим матрицу из
коэффициентов при переменных х4 и у1,
которые отсутствуют в третьем уравнении:
|
Уравнения, из которых взяты коэффициенты при переменных
|
Переменные
|
|
у1
|
x4
|
|
1
|
-1
|
0
|
|
2
|
0
|
a24
|
Определитель
данной матрицы равен
 ,
,
а ее ранг — 2. Значит достаточное условие идентификации выполнено, и
третье уравнение можно считать идентифицируемым.
Таким
образом, все три уравнения заданной системы идентифицируемы, а значит, идентифицируема
и вся система в целом.
Задача
2б
Используя
матрицу коэффициентов
модели в исходных данных, записываем систему одновременных уравнений регрессии в структурной форме:
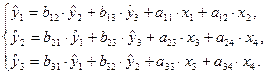
Проверим
каждое уравнение системы на выполнение необходимого и достаточного условия
идентификации.
В первом уравнении три эндогенные
переменные: y1, y2 и y3
(H=3). В нем отсутствуют экзогенные переменные x3 и x4 (D=2). Необходимое условие
идентификации  выполнено. Для проверки на достаточное
условие составим матрицу из коэффициентов при переменных x3 и x4, отсутствующих
в данном уравнении, но имеющихся в системе:
выполнено. Для проверки на достаточное
условие составим матрицу из коэффициентов при переменных x3 и x4, отсутствующих
в данном уравнении, но имеющихся в системе:
|
Уравнения, из которых взяты коэффициенты при переменных
|
Переменные
|
|
x3
|
x4
|
|
2
|
a23
|
a24
|
|
3
|
a33
|
a34
|
Определитель
матрицы не равен нулю:
 ,
,
а ее ранг матрицы равен 2. В заданной
системе уравнений три эндогенные переменные — y1, y2
и y3. Если  , то это означает, что достаточное условие идентификации для
данного уравнения выполнено. Первое уравнение считается идентифицируемым.
, то это означает, что достаточное условие идентификации для
данного уравнения выполнено. Первое уравнение считается идентифицируемым.
Во втором уравнении три эндогенные
переменные: y1, y2 и
y3 (H=3). В нем отсутствует экзогенные переменные x1 и x2 (D=2). Необходимое условие
идентификации  выполнено. Для проверки на достаточное
условие составим матрицу из коэффициентов при переменных x1 и x2, отсутствующих
в данном уравнении, но имеющихся в системе:
выполнено. Для проверки на достаточное
условие составим матрицу из коэффициентов при переменных x1 и x2, отсутствующих
в данном уравнении, но имеющихся в системе:
|
Уравнения, из которых взяты коэффициенты при переменных
|
Переменные
|
|
x1
|
x2
|
|
1
|
a11
|
a12
|
|
3
|
0
|
0
|
Определитель
матрицы не равен нулю:
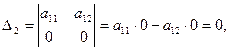 ,
,
а ее ранг матрицы равен 2. Значит, достаточное
условие идентификации для данного уравнения выполнено. Второе уравнение считается
идентифицируемым.
В третьем уравнении три эндогенные
переменные: y1, y2
и y3 (H=3). В нем отсутствует одна
экзогенная переменная x1 и x2
(D=2). Необходимое условие идентификации  выполнено. Для проверки на достаточное условие
составим матрицу из коэффициентов при переменных x1 и x2, отсутствующих
в данном уравнении, но имеющихся в системе:
выполнено. Для проверки на достаточное условие
составим матрицу из коэффициентов при переменных x1 и x2, отсутствующих
в данном уравнении, но имеющихся в системе:
|
Уравнения, из которых взяты коэффициенты при переменных
|
Переменные
|
|
x1
|
x2
|
|
1
|
a11
|
a12
|
|
2
|
0
|
0
|
Определитель
матрицы не равен нулю:
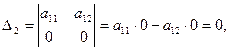 ,
,
а ее ранг матрицы равен 2. Значит, достаточное
условие идентификации для данного уравнения выполнено. Третье уравнение считается
идентифицируемым.
Таким
образом, первое уравнение заданной системы идентифицируемо, второе — идентифицируемо,
а третье — идентифицируемо. Если хотя бы одно уравнение системы
неидентифицируемо, то вся система считается неидентифицируемой. Данная система
является идентифицируемой и имеет статистическое решение.
Задача
2в
По
данным таблицы для своего варианта, используя косвенный метод наименьших
квадратов, построить структурную форму модели вида:

|
Вариант
|
n
|
у1
|
у2
|
х1
|
х2
|
|
9
|
1
|
25,1
|
21,8
|
8
|
7
|
|
2
|
41,7
|
33,8
|
10
|
14
|
|
3
|
12,5
|
12,5
|
7
|
1
|
|
4
|
25,9
|
23,4
|
7
|
8
|
|
5
|
41,7
|
36,0
|
5
|
17
|
|
6
|
9,4
|
11,4
|
2
|
2
|
РЕШЕНИЕ
С помощью табличного процессора EXCEL строим
два приведенных уравнения системы одновременных уравнений регрессии (меню «Сервис» ® «Анализ данных…»
® «Регрессия»):

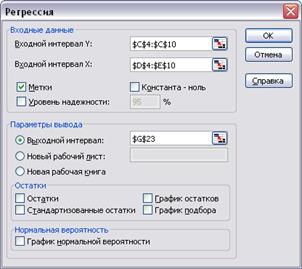
Данные уравнения образуют приведенную
форму системы одновременных уравнений регрессии:
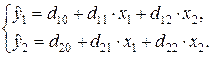
Коэффициенты приведенной формы имеют
следующие значения: d10»3,06; d11»1,06; d12»1,97; d20»7,43; d21»0,49 и d22»1,54 (см. прил.).
Таким образом, приведенная форма системы
уравнений имеет вид:

Определим коэффициенты структурной
формы системы уравнений

Структурные коэффициенты определяются по
формулам:
 ;
;
 ;
;
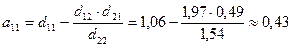 ;
;
 ;
;
 ;
;
 .
.
Окончательно структурная форма системы одновременных
уравнений регрессии примет вид:

ПРИЛОЖЕНИЕ: компьютерная распечатка на 1 листе.