МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО
ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ВСЕРОССИЙСКИЙ
ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА ЭКОНОМИКО-МАТЕМАТИЧЕСКИХ МЕТОДОВ И МОДЕЛЕЙ
К О Н Т Р О Л Ь Н А
Я Р А Б О Т А
по дисциплине
Эконометрика
Вариант 8
Выполнил:
студент III курса
специальность ФИНАНСЫ И КРЕДИТ
Проверил:
должность
________________
подпись
Липецк 2009
Задача
По предприятиям легкой
промышленности региона получена информация, характеризующая зависимость объема
выпуска продукции (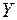
, млн. руб.) от объема капиталовложений (
, млн. руб.):
|
|
17
|
22
|
10
|
7
|
12
|
21
|
14
|
7
|
20
|
3
|
|
|
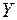
26
|
27
|
22
|
19
|
21
|
26
|
20
|
15
|
30
|
13
|
Требуется:
1.
Найти
параметры уравнения линейной регрессии, дать экономическую интерпретацию
коэффициента регрессии.
2.
Вычислить
остатки; найти остаточную сумму квадратов; оценить дисперсию остатков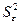 
; построить график остатков.
3.
Проверить
выполнение предпосылок МНК.
4.
Осуществить
проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента 
5.
Вычислить
коэффициент детерминации, проверить значимость уравнения регрессии с помощью 
- критерия Фишера 
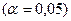, найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.
6.
Осуществить
прогнозирование среднего значения показателя 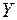при уровне
значимости 
, если прогнозное значения фактора Х составит
80% от его максимального значения.
7.
Представить
графически: фактические и модельные значения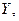 
точки прогноза.
8.
Составить
уравнения нелинейной регрессии:
·
гиперболической;
степенной; показательной.
Привести
графики построенных уравнений регрессии.
9.
Для
указанных моделей найти коэффициенты детерминации, коэффициенты эластичности и
средние относительные ошибки аппроксимации.
Сравнить модели по этим характеристикам и сделать вывод.
Решение.
1. Уравнение линейной регрессии
имеет следующий вид:
ŷ=а+b*x , где
,
.
Построим рабочую таблицу:
|
t
|
y
|
x
|
yx
|
xx
|
(yi-у
ср)
|
(yi-у
ср)2
|
(хi-х
ср)
|
(хi-х
ср)2
|
ў
|
εi=yi-
ўi
|
[εi/yi]*100
|
(yi-у
ср)*(хi-х ср)
|
|
1
|
26
|
17
|
442
|
289
|
4,1
|
16,81
|
3,7
|
13,69
|
24,71
|
1,29
|
4,94%
|
15,17
|
|
2
|
27
|
22
|
594
|
484
|
5,1
|
26,01
|
8,7
|
75,69
|
28,52
|
-1,52
|
5,62%
|
44,37
|
|
3
|
22
|
10
|
220
|
100
|
0,1
|
0,01
|
-3,3
|
10,89
|
19,39
|
2,61
|
11,87%
|
-0,33
|
|
4
|
19
|
7
|
133
|
49
|
-2,9
|
8,41
|
-6,3
|
39,69
|
17,11
|
1,89
|
9,96%
|
18,27
|
|
5
|
21
|
12
|
252
|
144
|
-0,9
|
0,81
|
-1,3
|
1,69
|
20,91
|
0,09
|
0,42%
|
1,17
|
|
6
|
26
|
21
|
546
|
441
|
4,1
|
16,81
|
7,7
|
59,29
|
27,76
|
-1,76
|
6,76%
|
31,57
|
|
7
|
20
|
14
|
280
|
196
|
-1,9
|
3,61
|
0,7
|
0,49
|
22,43
|
-2,43
|
12,16%
|
-1,33
|
|
8
|
15
|
7
|
105
|
49
|
-6,9
|
47,61
|
-6,3
|
39,69
|
17,11
|
-2,11
|
14,05%
|
43,47
|
|
9
|
30
|
20
|
600
|
400
|
8,1
|
65,61
|
6,7
|
44,89
|
27,00
|
3,00
|
10,01%
|
54,27
|
|
10
|
13
|
3
|
39
|
9
|
-8,9
|
79,21
|
-10,3
|
106,09
|
14,06
|
-1,06
|
8,18%
|
91,67
|
|
итого
|
219,00
|
133,00
|
3211,00
|
2161,00
|
|
264,90
|
|
392,10
|
|
|
83,99%
|
298,3
|
|
ср.знач.
|
21,90
|
13,30
|
321,10
|
216,10
|
|
|
|
|
|
|
|
|
|
диспер.
|
29,43
|
43,57
|
|
|
|
|
|
|
|
|
|
|
b=
a=21,9-0,76*13,3=11,78
=11,78+0,76* x.
Таким образом, с
увеличением объема капиталовложений на 1 млн.руб. объем выпуска продукции
увеличится на 0,76 млн.руб. Это свидетельствует об эффективности работы
предприятий.
Определим линейный коэффициент
парной корреляции по следующей формуле:
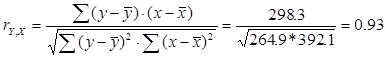
Можно сказать, что связь
между объемом капиталовложений Х и объемом выпуска продукции Y прямая, достаточно сильная.
2.
5. Коэффициент
детерминации рассчитывается по формуле:
Вариация результата Y (объема выпуска продукции) на 85,7%
объясняется вариацией фактора Х (объемом капиталовложений).
Оценка значимости
уравнения регрессии проводится с помощью F-Критерия Фишера:
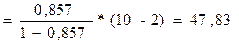
F>Fтабл=5,32 для α=0,05, k1=m=1. k2=n-m-1=8
Уравнение регрессии с
вероятностью 0,95 в целом статистически значимое т.к. F>Fтабл.
Средняя относительная
ошибка аппроксимации находится по формуле:
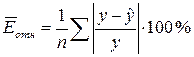=0,8399*0,1*100%=8,4%
В среднем расчетные
значения ŷ для линейной модели отличаются от фактических значений на 8,4%.
Так как 
=8,40% < 10%, то ошибка считается приемлемой, что
говорит о хорошей точности модели.