Контрольная работа № 1
1) Вычислить
определитель матрицы С=А2 +
3А – Е разложением по второй строке, где  , Е –
единичная матрица. Являются ли столбцы
матрицы С линейно независимыми?
, Е –
единичная матрица. Являются ли столбцы
матрицы С линейно независимыми?
РЕШЕНИЕ:

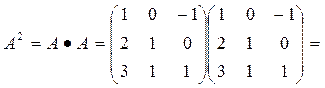
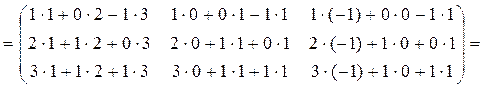
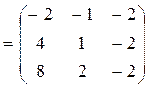
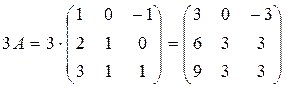
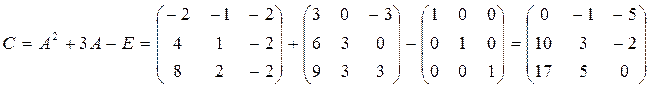
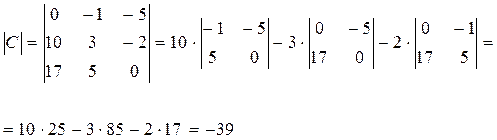
Поскольку 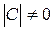 , то столбцы матрицы С являются линейно независимыми.
, то столбцы матрицы С являются линейно независимыми.
2) Найти предел: 
РЕШЕНИЕ:
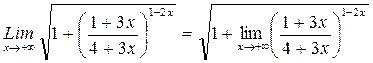

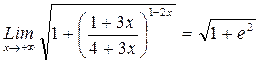
3) Найти производную функции: 
РЕШЕНИЕ:
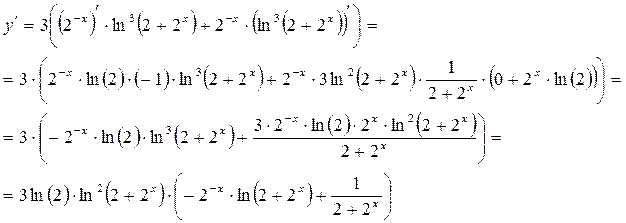
4) Площадь,
занимаемая печатным текстом, составляет на странице книги 432 см2.
Ширина полей вверху и внизу страницы составляет 2 см., а ширина боковых полей
по 1,5 см.
Каковы должны быть ширина и высота страницы, чтобы количество израсходованной
бумаги было наименьшим?
РЕШЕНИЕ:
Пусть х – ширина страницы, тогда (х-3) – ширина печатной страницы.
Поскольку площадь печатной площади равна 432 (см2), то значит высота
печатной площади равна  см., а высота
страницы равна
см., а высота
страницы равна  см.
см.
 Тогда количество израсходованной
бумаги равно
Тогда количество израсходованной
бумаги равно  см2
см2
Пусть f(x) – количество
израсходованной бумаги. Найдём минимум f(x) с помощью производной.
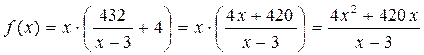
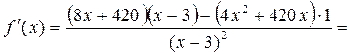


 не подходит, т. к. отрицательное число
не подходит, т. к. отрицательное число  см. ширина
страницы. Тогда высота страницы равна
см. ширина
страницы. Тогда высота страницы равна 
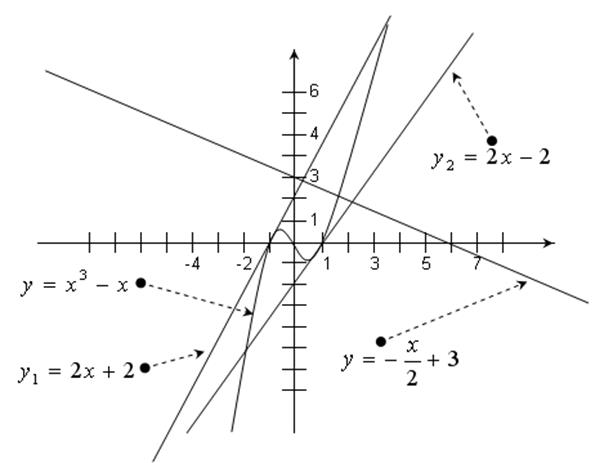
5) Составить
уравнения касательных к графику функций 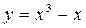 , перпендикулярных
прямой, пересекающейся с осью
, перпендикулярных
прямой, пересекающейся с осью  в точке
в точке
 и с осью
и с осью  в точке
в точке  . Сделать
чертеж.
. Сделать
чертеж.
РЕШЕНИЕ:
Найдём уравнение прямой, пересекающейся с осью  в точке
в точке  , а с осью
, а с осью  в точке
в точке  .
.
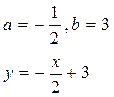
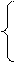
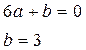

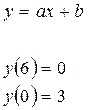
Эта
прямая имеет угловой коэффициент: 
Значит
управления касательных к графику будут иметь угловой коэффициент 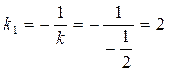
 Найдём точки на графике функции
Найдём точки на графике функции 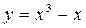 , в которых
угловой коэффициент равен 2, т. е. такие, где
, в которых
угловой коэффициент равен 2, т. е. такие, где 
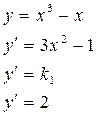
Напишем уравнения
касательных:



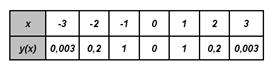
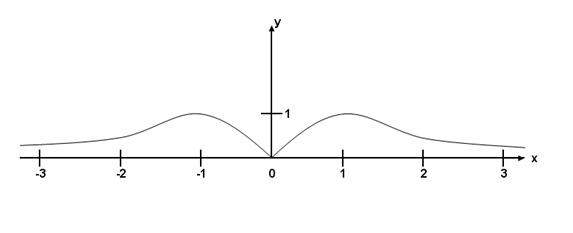
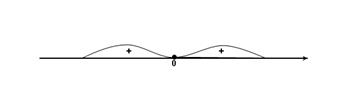
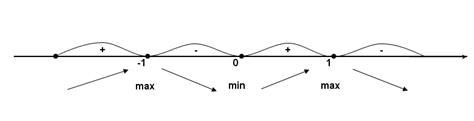
6) Исследовать функцию 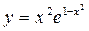 и схематично построить её
график.
и схематично построить её
график.
РЕШЕНИЕ:
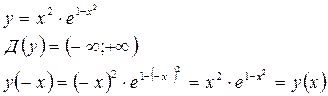
Значит
 - чётная
функция и график симметричен относительно оси
- чётная
функция и график симметричен относительно оси  ,
,
 - не периодична, т. к.
не содержит тригонометрических функций
- не периодична, т. к.
не содержит тригонометрических функций
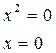
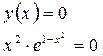

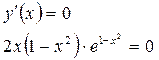
 или
или 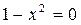
 или
или 



Найдём асимптоты:
Вертикальных асимптот нет, т. к. нет
точек разрыва.
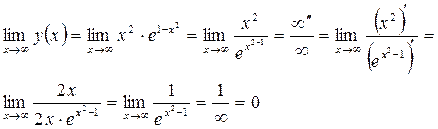
Значит  - горизонтальная асимптота, при
- горизонтальная асимптота, при 
Наклонных
асимптот нет, поскольку есть горизонтальная.