§2. Следствие из аксиом векторного пространства
Из аксиом I-X можно
вывести целый ряд предложений.
Теорема
2.1. Существует единственный нулевой
вектор.
Доказательство:
Предложим, что
существует два различных вектора 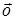 и
и  таких, что
таких, что 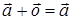 и
и  для любого вектора
для любого вектора  .
.
Положим  . Тогда
. Тогда
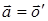 и
и  (1)
(1)
Положим теперь  . Аналогично получим:
. Аналогично получим:
 и
и  (2)
(2)
Так как  (по аксиоме II), то из
(1) и (2) следует, что
(по аксиоме II), то из
(1) и (2) следует, что  .
.
Таким образом, векторное
пространство содержит единственный вектор 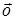 , удовлетворяющий равенству
, удовлетворяющий равенству 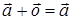 .
.
Теорема
2.2. Для любого вектора  существует
единственный противоположный вектор
существует
единственный противоположный вектор 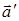 .
.
Или:
 и
и 
Доказательство:
Допустим, что  и
и 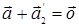 и
и  , т.е. существует
, т.е. существует  , имеющий два различных противоположных вектора
, имеющий два различных противоположных вектора 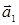 и
и  .
.
 и (1)
и (1)
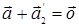 (2)
(2)
Тогда
 и
и  (3)
(3)
Левые части равенств (3) равны между собой. Действительно:
 (4)
(4)
Из равенства (3) и (4) следует, что 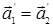 .
.
Теорема
2.3. Для любых векторов  и
и  существует
единственный вектор
существует
единственный вектор 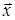 , такой, что
, такой, что 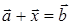 .
.
Доказательство:
I. Существование. Убедимся,
что в качестве вектора 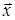 можно будет выбрать
вектор
можно будет выбрать
вектор  . В самом деле,
. В самом деле,
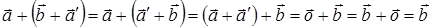
Таким образом, для векторов  и
и  существует вектор
существует вектор 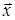 , удовлетворяющий равенству:
, удовлетворяющий равенству:
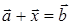 .
.
II. Единственность (от
противного). Пусть
 и
и  (1)
(1)
Тогда:
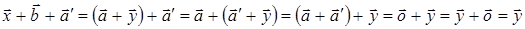
Отсюда 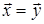 . Получим противоречие с допущением. Таким образом, единственность
вектора
. Получим противоречие с допущением. Таким образом, единственность
вектора 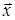 доказана.
доказана.
Определение
2.1. Вектор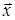 , удовлетворяющий равенству
, удовлетворяющий равенству 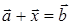 , называется разностью векторов
, называется разностью векторов  и
и  , и обозначается через
, и обозначается через  -
-  .
.
Таким образом
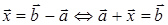
Теорема 2.3., как видно, вводит на множестве v новую операцию "–":
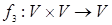
называемую вычитанием,
которая является обратной по отношению к операции сложения.
Следствие 1. 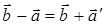
Теорема 2.4. 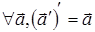
Доказательство:
 , т.к.
, т.к.  - вектор,
противоположный вектору
- вектор,
противоположный вектору 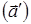 . Тогда
. Тогда
 Ч.т.д.
Ч.т.д.
Теорема 2.5. 
Доказательство:
Имеем:
 ;
; 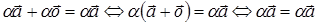
Отсюда следует, что  .
.
Ч.т.д.
Теорема 2.6.  .
.
Доказательство:
Имеем:


Отсюда следует, что  .
.
Теорема
2.7. 
Доказательство:
Имеем:
 (по Теореме
2.6.)
(по Теореме
2.6.)
Отсюда следует, что  .
.
Следствие 2.  .
.
Теорема 2.8. 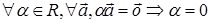 или
или  .
.
Доказательство:
Возможны два случая:
I.  и
и
II.
 .
.
I. Если  , то дизъюнкция
, то дизъюнкция  или
или  истинна и теорема
доказана.
истинна и теорема
доказана.
II. Пусть  . Тогда существует число
. Тогда существует число  , отсюда имеем:
, отсюда имеем:
 (по условию Т. 2.5.)
(по условию Т. 2.5.) 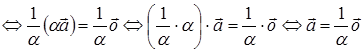 ,
,
(по Т. 2.5.)  .
.
Таким образом, в случае II имеем, что  .
.
Итак, если  , то
, то  или
или  .
.
Теорема 2.9.  .
.
Доказательство:
Для того, чтобы установить, что вектор  является
противоположным для вектора
является
противоположным для вектора  , необходимо и достаточно проверить, выполняется ли следующее
равенство:
, необходимо и достаточно проверить, выполняется ли следующее
равенство:
 , или все равно, что
, или все равно, что  .
.
Имеем:

Таким образом  или
или  . И, следовательно,
. И, следовательно,  .
.
Рассмотренные свойства операций над векторами аналогичны
соответствующим свойствам арифметических операций над числом. Так, например,
сумма конечного числа векторов, как и сумма в любой коммуникативной группе, не
зависит ни от порядка слагаемых в этой сумме, ни от способа расстановки скобок:
 и т.д.
и т.д.
Однако между векторной и числовой алгеброй существуют
серьезные отличия. Одно из наиболее существенных отличий состоит в том, что
множество векторов не является упорядоченным, т.е. для векторов нельзя ввести
отношение «меньше» и «больше». Например для двух противоположных чисел  и
и  мы знаем, что
мы знаем, что  и, что одно из этих
двух чисел больше 0, а другое – меньше 0. Для векторов же, удовлетворяющих
равенству
и, что одно из этих
двух чисел больше 0, а другое – меньше 0. Для векторов же, удовлетворяющих
равенству 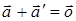 , постановка вопроса о том, какой из векторов
, постановка вопроса о том, какой из векторов  или
или  больше нулевого, а какой
меньше нулевого, бессмысленна.
больше нулевого, а какой
меньше нулевого, бессмысленна.