II. Круг идей П.Л. Чебышева.

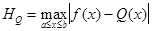Пусть даны замкнутый (конечный или бесконечный) интервал [a,b] числовой оси и две вещественные непрерывные в [a,b] функции f(x) и S(x). Составим выражение: (*), где m и n заданы и поставим задачу найти вещественные параметры p₀,p₁...p_m; q₀,q₁...q_n так, чтобы уклонение  Q(x) от f(x) было наименьшим.

В частном случае, когда S(x)=1, m=0 и интервал [a,b] конечен, поставленная задача переходит в задачу о наилучшем приближении в пространстве С заданной функции с помощью многочлена степени n.

Будем полагать, что m=n-k, кроме того, если интервалом [a,b] является вся числовая ось, мы будем предполагать, что  и будем рассматривать только те функции, для которых 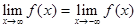, m условимся считать чётным.

2.1 Обобщённая теорема Валле-Пуссена.

Если многочлены 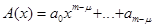; 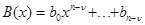, где  и 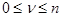, , 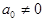не имеют общего делителя , а выражение  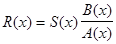в интервале [a,b] остаётся конечным и если разность f(x)-R(x) принимает в последовательных точках x₁<x₂<...<x_n интервала [a,b], отличные от значения 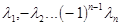 с чередующимися знаками, N=m+n-d+2, , то для каждой функции  имеет место неравенство: 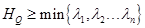  , где 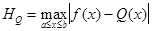. Это же неравенство имеет место, если R(x)=0 и N=n+2.

Значение этой теоремы состоит в том, что она даёт возможность получить для погрешности наилучшего приближения некоторую оценку снизу.

Теорема существования.

Среди функций Q(x) существует по крайней мере одна, для которой H_Q имеет наименьшее значение.

Т.о., пусть Н- есть нижняя грань множества всех H_Q. По определению, следовательно, существует бесконечная последовательность функций Q_i(x), для которой .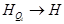

2.2. Теорема Чебышева.   

Функция Р(х), которая из всех функций вида Q(x) наименее уклоняется в [a,b] от функции f(x), единственна.

Эта функция вполне характеризуется таким своим свойством, если она приведена к виду ,  и 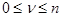,  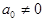и дробь  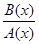несократима, то число N последовательных точек интервала [a,b], в котором разность f(x)-P(x) принимает с чередующимися знаками значение Н_р, не менее, чем m+n-d+2, где d=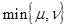, а если P(x)=0, то .

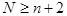Теорема Чебышева показывает, что существует единственная функция P(x), дающая наилучшее приближение к данной функции f(x) (т.е. наименее отклоняется от f(x)) в данном нормированном пространстве.

Случай аппроксимации многочленами.

Особенно важным является частный случай, когда S(x)=1, m=0 и интервал [a,b] конечен. В этом случае мы получаем теорему:

многочлен n-й степени P(x), который наименее уклоняется (в метрике пространства С) от заданной непрерывной функции f(x), единственен и вполне характеризуется тем, что число последовательных точек интервала [a,b], в которых разность f(x)-P(x) принимает с чередующимися знаками значение  не меньше, чем n+2.

2.3 Переход к периодическим функциям.

Допустим, что 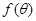- есть непрерывная периодическая функция с периодом , которую нужно наилучшим образом аппроксимировать на всей оси при помощи тригонометрической суммы: 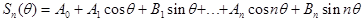 порядка n. Сделаем замену переменной  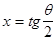так, что интервалу  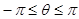будет соответствовать интервал .

Т.к. 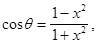 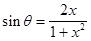  и так как  есть многочлены степени к от 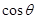, то после преобразования мы получим 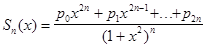. Следовательно, наша задача сводится к наилучшему (в интервале 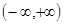) приближению функции F(x)=f(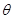) при помощи выражения вида: 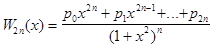. Выражение W_2n(x) можно рассматривать как частный случай выражения Q(x), если положить m=0, 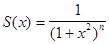. Легко видеть, что общие теоремы применимы, и теорема Чебышева гласит:

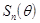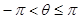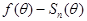тригонометрическая сумма n-го порядка , которая наименее уклоняется на всей оси от заданной непрерывной периодической функции, единственна и вполне характеризуется тем, что число последовательных точек интервала  (или какого- нибудь открытого полуинтервала длиной 2), в которых разность  принимает с чередующимися знаками значение max|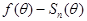| не меньше, чем 2n+2.

Одну и ту же функцию f(x) в (0,) можно разложить в ряд по sin, по cos, по sin и cos, т.к. если f(x) определена на (0,), то доопределить f(x) на  можно бесконечным множеством способов. Следовательно, задача о разложении f(x) в ряд имеет бесчисленное множество решений. Из всех этих решений выделяются 2:

Если f(x) доопределить чётным образом, то получим ряд только по cos кратных дуг;

Если f(x) доопределить нечётным образом, то получим ряд только по sin.

Пример: f(x)=x на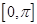

  ,

;

;

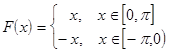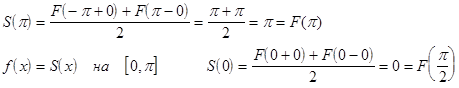
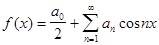
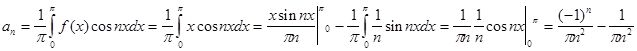
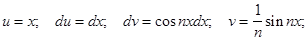
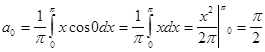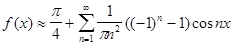
Для sin аналогично, только f(x)- нечётная.

2.4 Обобщение теоремы Чебышева.

Мы рассмотрели алгебраические и тригонометрические многочлены на некотором интервале и сформулировали для них теорему Чебышева об аппроксимации этих функций. Теперь рассмотрим произвольную, непрерывную на [a,b] вещественную функцию.

Рассмотрим систему вещественных непрерывных функций f₁(x),f₂(x)...f_n(x) в конечном или бесконечном интервале [a,b], которая удовлетворяет условиям Хаара: единственность полинома наименьшего уклонения для каждой функции f(P) будет тогда и только тогда, когда каждый полином F(P,x)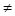0 имеет в ограниченном замкнутом точечном множестве  не более n-1 различных нулей.

Такую систему называют системой Чебышева относительно интервала [a,b].

Лемма: Пусть x₁,x₂...x_n-1 произвольно взятые различные точки из интервала [a,b]. В таком случае существует (и с точностью до постоянного множителя только 1) нетривиальный полином 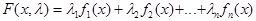, который имеет своими нулями следующие точки:

 

Других нулей у этого полинома нет, и, если т. x_k лежит внутри [a,b], то при переходе через неё полином F(x,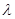) меняет знак.

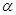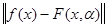Обобщение: Если S- есть система Чебышева относительно интервала [a,b], а f(x)- произвольная непрерывная в [a,b] вещественная функция, то полином F(x,), который в метрике С наименее уклоняется в [a,b] от f(x) вполне определяется тем, что разность  принимает с чередующимися знаками своё максимальное значение по крайней мере в n+1 последовательных точках интервала [a,b].

Теперь мы можем рассматривать функции в произвольных нормированных пространствах.