МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ОТКРЫТЫЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Контрольная работа
по курсу «Проектирование автоматических систем»
Проектирование двухстепенного манипулятора с самонастройкой
Выполнила: Губарева О.Е.
Заочная форма обучения
Курс V
Специальность 210100
№ зачетной книжки 607932
Проверил преподаватель: Воронин Ю.Ю.
Москва 2010 г.
1. Уравнение динамики исполнительного механизма двухстепенного манипулятора
Параметры манипулятора для 2-го варианта
М1
,(кг)= 10
М2
,(кг)=15
l1
,(м)=1,8
l1
,(м)=3
Входными сигналами манипулятора служат управляющее напряжение на приводе. Выходными сигналами служат обобщенные координаты q.
М1
, М2
– масса первого и второго звена;
l1
, l2
– длины приводов.
Динамика данного исполнительного механизма описывается уравнением:
А(q)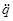 + B(q, + B(q,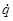 ) + G(q) = ) + G(q) = 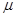 [H•м] [H•м]
q = 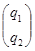 - обобщенные координаты манипулятора; - обобщенные координаты манипулятора;
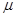 = = 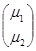 - управление (момент нагрузки приводов всех подвижностей). - управление (момент нагрузки приводов всех подвижностей).
А(q) – матрица инерции (2×2);
G(q) – матрица гравитационных сил;
B(q,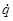 ) – матрица моментов скоростных сил; ) – матрица моментов скоростных сил;
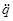 - ускорение ротора. - ускорение ротора.
B(q,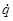 ) = ) = 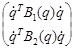 
B1
(q) иB2
(q) – симметричные матрицы 2×2;
G(q) – моменты гравитационных сил (сил тяжести).
Выражения для матриц
1. Для матрицы А(q) = 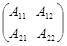 , где , где
Элемент А11
определяет момент инерции нагрузки на первый привод манипулятора
А11
= Н1
+Н2
+Н3
+М2
· l1
·l2
· Cosq2
, где
Н1
= 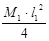
Н1
= (10 · 1,82
)/4= 8,1
Н2
= М2
l1
2
Н2
= 15 · 1,82
= 48,6
Н3
= 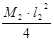
Н3
= (15 · 32
) / 4 = 33,75
А11
= 8,1 + 48,6 + 33,75 + 15 ·1,8 ·3 · Cosq2
= 90,45 + 81 Cosq2
А12
= А21
= Н3
+ ½М2
l1
l2
Cosq2
– определяют взаимовлияние друг на друга двух степеней подвижности.
А12
= А21
= 33,75 + ½(15 · 1,8 · 3) · Cosq2
= 33,75 +40,5 Cosq2
А22
= Н3
– определяет момент инерции на второй привод;
А22
= 33,75
А(q) = 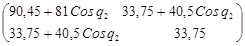
2. Для матрицы B1
(q) иB2
(q):
B1
(q) = 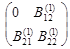 , ,
где
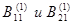 = -½ М2
l1
l2
Sinq2 = -½ М2
l1
l2
Sinq2
 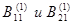 = = 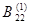 = - ½ (15 ·1,8 ·3) Sin q2
= - 40,5 Sin q2 = - ½ (15 ·1,8 ·3) Sin q2
= - 40,5 Sin q2
B1
(q) = 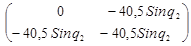 , ,
B2
(q) =  , ,
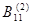 = ½ М2
l1
l2
Sinq2 = ½ М2
l1
l2
Sinq2
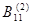 = 40,5 Sin q2 = 40,5 Sin q2
B2
(q) = 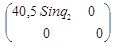
При расчете управления потребуются собственные числа:
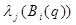 матриц В1
(q) и В2
(q). Эти матрицы симметричные. матриц В1
(q) и В2
(q). Эти матрицы симметричные.
Собственные числа 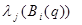 находят из уравнения: находят из уравнения:
det  = 0 = 0
B1
(q) -  E = E = 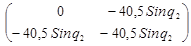 - -   = =
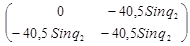 - -
- 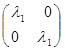 = = 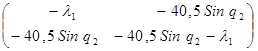
 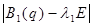 = = 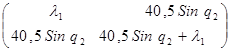
det 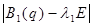 = = 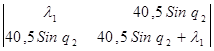 = =  (40,5 Sin q2
+ (40,5 Sin q2
+  ) – ) –
1640,25Sin2
q2
= 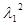 +40,5 Sinq2 +40,5 Sinq2
 - 1640,25 Sin2
q2 - 1640,25 Sin2
q2
Решим уравнение:
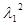 +40,5 Sinq2 +40,5 Sinq2
 - 1640,25 Sin2
q2
= 0 - 1640,25 Sin2
q2
= 0
 = 25 Sinq2 = 25 Sinq2
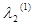 = -65,5 Sinq2 = -65,5 Sinq2
Таким образом найдены собственные числа для матрицы В1
(q).
B2
(q) -  E = E = 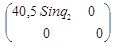 - -   = = 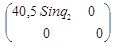 - - 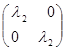 = =
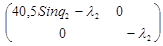
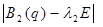 = = 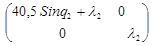
det 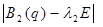 = = 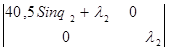 = =  (40,5 Sinq2
+ (40,5 Sinq2
+  ) )
 (40,5Sinq2
+ (40,5Sinq2
+  ) = 0 ) = 0
40,5 Sinq2
+ 
 = - 40,5 Sinq2 = - 40,5 Sinq2
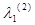 = 0 = 0
 = - 40,5 Sinq2 = - 40,5 Sinq2
Таким образом найдены собственные числа для матрицы В2
(q).
Для моментов всех тяжестей матрица моментов гравитационных сил G(q):
а) для первого привода:
G1
(q) =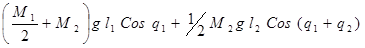 - момент тяжести для первого привода - момент тяжести для первого привода
G1
(q) = 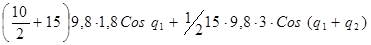
=352,8·Cosq1
+220,5·Cos(q1
+q2
)
G2
(q) = 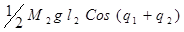 = 220,5Cos (q1
+ q2
) = 220,5Cos (q1
+ q2
)
Выразим частные производные:
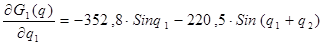
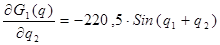
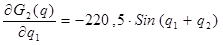

2. Управление двухстепенного манипулятора с самонастройкой по эталонной модели
Требуется сформировать такое управление 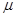 , при котором динамика манипулятора описывалась бы уравнением желаемой модели: , при котором динамика манипулятора описывалась бы уравнением желаемой модели:
Управление 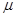 описывается уравнением: описывается уравнением:
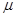 = uЛ
+ d, где = uЛ
+ d, где
Здесь qd
(t) – заданная траектория движения манипулятора в обобщенных координатах.
uЛ
– линейная составляющая управления для упрощенной модели манипулятора;
d – сигнал самонастройки, позволяющий обеспечить нужное поведение системы для полной модели объекта управления.
Для траекторных задач, где известна траектория qd
(t) системы, можно желаемую модель выбрать так, чтобы не было ошибки слежения по траектории:
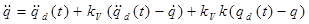
uЛ
=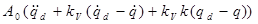 , где , где
А0
– постоянная матрица 2×2
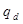 = = 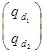 - вход - вход
kV
= const; k = const – параметры желаемой модели.
Для формирования сигнала самонастройки вводится эталонная модель системы:
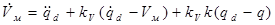 , где , где
 - выходной сигнал скорости эталонной модели. - выходной сигнал скорости эталонной модели.
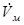 - ускорение эталонной модели. - ускорение эталонной модели.
В системе управления формируется сигнал ошибки по скорости  , несущий информацию об отклонении движения манипулятора от заданной эталонной модели. Этот сигнал используется в блоке самонастройки (БСН) для формирования дополнительного сигнала управления. БСН обеспечивает поддержание , несущий информацию об отклонении движения манипулятора от заданной эталонной модели. Этот сигнал используется в блоке самонастройки (БСН) для формирования дополнительного сигнала управления. БСН обеспечивает поддержание  . .
Таким образом, ошибка системы относительно эталонной модели е:
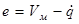
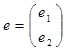
Уравнение сигнала самонастройки di
:
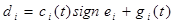 , здесь , здесь
сi
(t)sign еi
– разрывной сигнал переменной амплитуды, обеспечивающий наличие эталонного режима, в котором поддерживается еi
= 0.
Интегрирующая составляющая gi
(t)введена для компенсации гравитационных моментов Gi
(q).
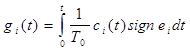
За счет регулировки коэффициентов сi
(t) в зависимости от составляющих системы можно осуществлять управление с малыми амплитудами разрыва составляющих в сигнале самонастройки. Причем, целесообразно получить сi
→ 0 при приближении к состоянию равновесия.
Тогда становится возможным обеспечить невысокие потери мощности приводов и нормальный тепловой режим их работы при управлении самонастройки.
Возьмем следующий закон формирования сигналов самонастройки:
 , где , где
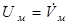
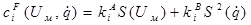
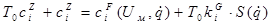 , i = 1, 2. , i = 1, 2.
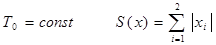
 Структурная схема самонастраивающейся системы
Структурная схема самонастраивающейся системы
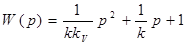 - передаточная функция системы. - передаточная функция системы.
3. Расчет параметров системы
Задается положение манипулятора:
      q1
= 900
q1 q1
= 900
q1
  q2
= 900 q2
= 900
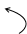 q2 q2
Для этого положения вычисляется А(q), которая задает значение А0
:
 А0
= А(q) А0
= А(q)
q1
= 900
q2
= 900
Берется второе положение манипулятора максимально удаленное от первого положения:
q1
= 1800
q2
= 00
 q1 q1
А0
= 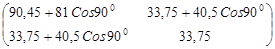 = = 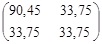
Для второго положения рассчитывается А(q).
А(q) =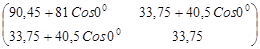 = = 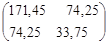
А(q) - А0
= 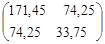 - - 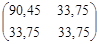 = = 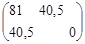
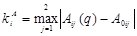 , i = 1, 2. , i = 1, 2.
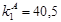
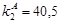
Рассчитаем B1
(q) и B2
(q) для первого положения (для второго положения они нулевые).
B1
(q) =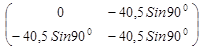 = = 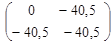
B2
(q) =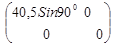 = =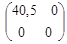
Рассчитаем 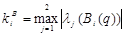 , i = 1, 2. , i = 1, 2.
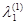 = 25 = 25
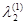 =-65,5 =-65,5
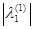 > >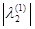 , следовательно , следовательно
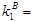 25 25
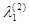 = 0 = 0
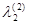 = -40,5 = -40,5
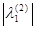 < < 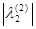 , следовательно , следовательно
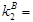 40,5 40,5
Рассчитаем 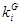 : :
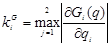 , i = 1, 2. , i = 1, 2.
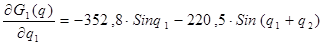 =-352,8 =-352,8
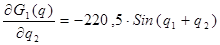
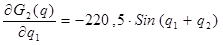

 > >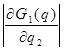 , следовательно , следовательно
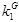 = 352,8 = 352,8
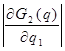 = = = 0, следовательно = 0, следовательно
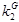 = 0 = 0
Таким образом, коэффициент настройки 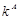 , учитывающий изменение матрицы манипулятора А(q): , учитывающий изменение матрицы манипулятора А(q):
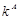 = (40,5; 40,5) = (40,5; 40,5)
Коэффициент настройки 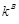 , учитывающий наличие моментов скоростных сил: , учитывающий наличие моментов скоростных сил:
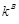 = (25; 40,5) = (25; 40,5)
Коэффициент настройки 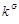 , учитывающий скорость изменения моментов сил тяжести при движении манипулятора: , учитывающий скорость изменения моментов сил тяжести при движении манипулятора:
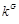 = (352,8; 0) = (352,8; 0)
|