Академия России
Кафедра Физики
Лекция
Переходные и импульсные характеристики электрических цепей
Орел 2009
Учебные и воспитательные цели:
Разъяснить слушателям сущность переходной и импульсной характеристик электрических цепей, показать связь между характеристиками, обратить внимание на применение рассматриваемых характеристик для анализа и синтеза ЭЦ, нацелить на качественную подготовку к практическому занятию.
Распределение времени лекции
Вступительная часть……………………………………………………5 мин.
Учебные вопросы:
1. Переходные характеристики электрических цепей………………15 мин.
2. Интегралы Дюамеля………………………………………………...25 мин.
3. Импульсные характеристики электрических цепей. Связь между характеристиками………………………………………….………...25 мин.
4. Интегралы свертки………………………………………………….15 мин.
Заключение……………………………………………………………5 мин.
1. Переходные характеристики электрических цепей
Переходная характеристика цепи (как и импульсная) относится к временным характеристикам цепи, т. е. выражает некоторый переходный процесс при заранее установленных воздействиях и начальных условиях.
Для сравнения электрических цепей по их реакции к этим воздействиям, необходимо цепи поставить в одинаковые условия. Наиболее простыми и удобными являются нулевые начальные условия.
Переходной характеристикой цепи
называют отношение реакции цепи на ступенчатое воздействие к величине этого воздействия при нулевых начальных условиях.
По определению 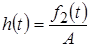 ,
,
где 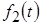 – реакция цепи на ступенчатое воздействие; – реакция цепи на ступенчатое воздействие;
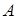 – величина ступенчатого воздействия [В] или [А]. – величина ступенчатого воздействия [В] или [А].
Так как 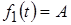 и и 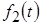 делится на величину воздействия (это вещественное число), то фактически делится на величину воздействия (это вещественное число), то фактически 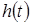 – реакция цепи на единичное ступенчатое воздействие. – реакция цепи на единичное ступенчатое воздействие.
Если переходная характеристика цепи известна (или может быть вычислена), то из формулы можно найти реакцию этой цепи на ступенчатое воздействие при нулевых НУ
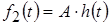 .
.
Установим связь между операторной передаточной функцией цепи, которая часто известна (или может быть найдена), и переходной характеристикой этой цепи. Для этого используем введенное понятие операторной передаточной функции:
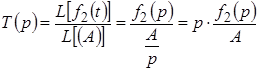 .
.
Отношение преобразованной по Лапласу реакции цепи к величине воздействия 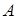 представляет собой операторную переходную характеристику цепи: представляет собой операторную переходную характеристику цепи:
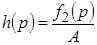 .
.
Следовательно 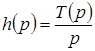 .
.
Отсюда находится операторная переходная характеристика цепи по операторной передаточной функции.
Для определения переходной характеристики цепи необходимо применить обратное преобразование Лапласа:
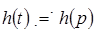 , ,
воспользовавшись таблицей соответствий или (предварительно) теоремой разложения.
Пример: определить переходную характеристику для реакции напряжение на емкости в последовательной 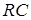 -цепи (рис. 1): -цепи (рис. 1):
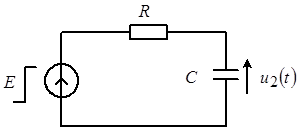
Рис. 1
Здесь реакция на ступенчатое воздействие величиной 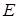 : :
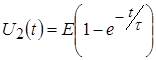 ,
,
откуда переходная характеристика:
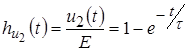 .
.
Переходные характеристики наиболее часто встречающихся цепей найдены и даны в справочной литературе.
2. Интегралы Дюамеля
Переходную характеристику часто используют для нахождения реакции цепи на сложное воздействие. Установим эти соотношения.
Условимся, что воздействие 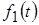 является непрерывной функцией и подводится к цепи в момент времени является непрерывной функцией и подводится к цепи в момент времени 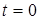 , а начальные условия – нулевые. , а начальные условия – нулевые.
Заданное воздействие 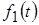 можно представить как сумму ступенчатого воздействия можно представить как сумму ступенчатого воздействия 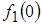 приложенного к цепи в момент приложенного к цепи в момент 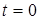 и бесконечно большого числа бесконечно малых ступенчатых воздействий, непрерывно следующих друг за другом. Одно из таких элементарных воздействий, соответствующих моменту приложения и бесконечно большого числа бесконечно малых ступенчатых воздействий, непрерывно следующих друг за другом. Одно из таких элементарных воздействий, соответствующих моменту приложения 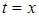 показано на рисунке 2. показано на рисунке 2.
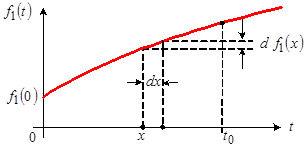
Рис. 2
Найдем значение реакции цепи в некоторый момент времени 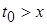 . .
Ступенчатое воздействие с перепадом 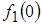 к моменту времени к моменту времени 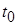 обуславливает реакцию, равную произведению перепада обуславливает реакцию, равную произведению перепада 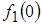 на значение переходной характеристики цепи при на значение переходной характеристики цепи при 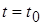 , т. е. равную: , т. е. равную:
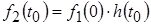 .
.
Бесконечно малое же ступенчатое воздействие с перепадом 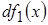 , обуславливает бесконечно малую реакцию , обуславливает бесконечно малую реакцию 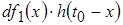 , где , где 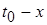 есть время, прошедшее от момента приложения воздействия до момента наблюдения. Так как по условию функция есть время, прошедшее от момента приложения воздействия до момента наблюдения. Так как по условию функция 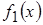 непрерывна, то: непрерывна, то:
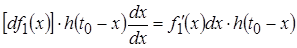 .
.
В соответствии с принципом наложения реакции 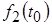 будет равна сумме реакций, обусловленных совокупностью воздействий, предшествующих моменту наблюдения будет равна сумме реакций, обусловленных совокупностью воздействий, предшествующих моменту наблюдения 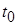 , т. е. , т. е.
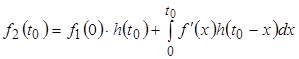 .
.
Обычно в последней формуле 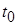 заменяют просто на заменяют просто на 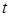 , поскольку найденная формула верна при любых значениях времени , поскольку найденная формула верна при любых значениях времени 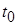 : :
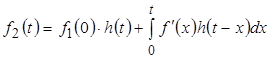 .
.
Или, после несложных преобразований:
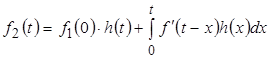 .
.
Любое из этих соотношений и решает задачу вычисления реакции 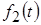 линейной электрической цепи на заданное непрерывное воздействие линейной электрической цепи на заданное непрерывное воздействие 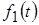 по известной переходной характеристики цепи по известной переходной характеристики цепи 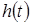 . Эти соотношения называют интегралами Дюамеля. . Эти соотношения называют интегралами Дюамеля.
3. Импульсные характеристики электрических цепей
Импульсной характеристикой цепи
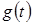 называют отношение реакции цепи на импульсное воздействие к площади этого воздействия при нулевых начальных условиях. называют отношение реакции цепи на импульсное воздействие к площади этого воздействия при нулевых начальных условиях.
По определению 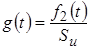 ,
,
где 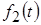 – реакция цепи на импульсное воздействие; – реакция цепи на импульсное воздействие;
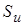 – площадь импульса воздействия. – площадь импульса воздействия.
По известной импульсной характеристике цепи можно найти реакцию цепи на заданное воздействие: 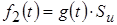 .
.
В качестве функции воздействия часто используется единичное импульсное воздействие называемое также дельта-функцией или функцией Дирака.
Дельта-функция – это функция всюду равная нулю, кроме 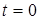 , а площадь ее равна единице ( , а площадь ее равна единице (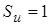 ): ):
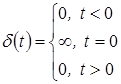 . .
К понятию дельта-функция можно прийти, рассматривая предел прямоугольного импульса высотой 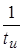 и длительностью и длительностью 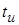 , когда , когда 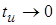 (рис. 3): (рис. 3):

Рис. 3
Установим связь между передаточной функцией цепи и ее импульсной характеристикой, для чего используем операторный метод.
По определению:
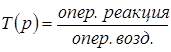 . .
Если воздействие (оригинал) рассматривать для наиболее общего случая в виде произведения площади импульса на дельта-функцию, т. е. в виде 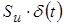 , то изображение этого воздействия согласно таблицы соответствий имеет вид: , то изображение этого воздействия согласно таблицы соответствий имеет вид:
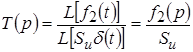 .
.
Тогда с другой стороны, отношение преобразованной по Лапласу реакции цепи к величине площади импульса воздействия, представляет собой операторную импульсную характеристику цепи:
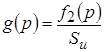 .
.
Следовательно, 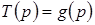 .
.
Для нахождения импульсной характеристики цепи 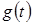 необходимо применить обратное преобразование Лапласа: необходимо применить обратное преобразование Лапласа:
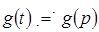 , т. е. фактически , т. е. фактически 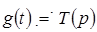 . .
Обобщая формулы, получим связь между операторной передаточной функцией цепи 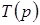 и операторными переходной и импульсной характеристиками цепи: и операторными переходной и импульсной характеристиками цепи:
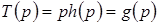 .
.
Таким образом, зная одну из характеристик цепи, можно определить любые другие.
Произведем тождественное преобразование равенства, прибавив к средней части 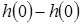 .
.
Тогда будем иметь 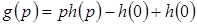 .
.
Поскольку 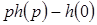 представляет собой изображение производной переходной характеристики, то исходное равенство можно переписать в виде: представляет собой изображение производной переходной характеристики, то исходное равенство можно переписать в виде:
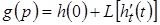 .
.
Переходя в область оригиналов, получаем формулу, позволяющую определить импульсную характеристику цепи по известной ее переходной характеристике:
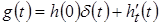 .
.
Если 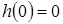 , то , то 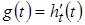 .
.
Обратное соотношение между указанными характеристиками имеет вид:
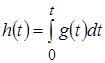 .
.
По передаточной функции 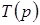 легко установить наличие в составе функции легко установить наличие в составе функции 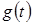 слагаемого слагаемого 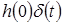 . .
Если степени числителя и знаменателя 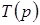 одинаковы, то рассматриваемое слагаемое будет присутствовать. Если же функция одинаковы, то рассматриваемое слагаемое будет присутствовать. Если же функция 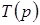 является правильной дробью, то этого слагаемого не будет. является правильной дробью, то этого слагаемого не будет.
Пример: определить импульсные характеристики для напряжений 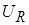 и и 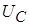 в последовательной в последовательной 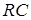 -цепи, показанной на рисунке 4. -цепи, показанной на рисунке 4.
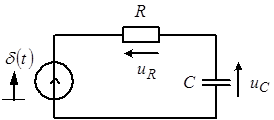
Рис. 4
Определим 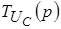 : :
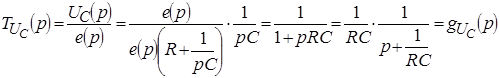 .
.
По таблице соответствий перейдем к оригиналу:
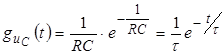 .
.
График этой функции показан на рисунке 5.
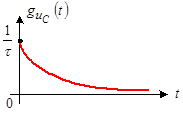
Рис. 5
Передаточная функция 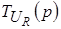 : :
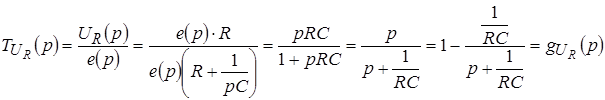 . .
Согласно таблице соответствий имеем:
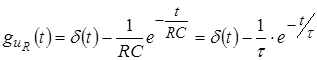 .
.
График полученной функции показан на рисунке 6.

Рис. 6
Укажем, что такие же выражения можно было получить с помощью соотношений, устанавливающих связь между 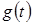 и и 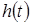 . .
Импульсная характеристика по физическому смыслу отражает собой процесс свободных колебаний и по этой причине можно утверждать, что в реальных цепях всегда должно выполняться условие:
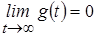 . .
4. Интегралы свертки (наложения)
Рассмотрим порядок определения реакции линейной электрической цепи на сложное воздействие, если известна импульсная характеристика этой цепи 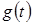 . Будем считать, что воздействие представляет собой кусочно-непрерывную функцию . Будем считать, что воздействие представляет собой кусочно-непрерывную функцию 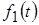 , показанную на рисунке 7. , показанную на рисунке 7.
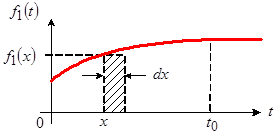
Рис. 7
Пусть требуется найти значение реакции 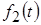 в некоторый момент времени в некоторый момент времени 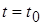 . Решая эту задачу, представим воздействие . Решая эту задачу, представим воздействие 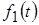 в виде суммы прямоугольных импульсов бесконечно малой длительности, один из которых, соответствующий моменту времени в виде суммы прямоугольных импульсов бесконечно малой длительности, один из которых, соответствующий моменту времени 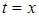 , показан на рисунке 7. Этот импульс характеризуется длительностью , показан на рисунке 7. Этот импульс характеризуется длительностью 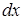 и высотой и высотой 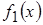 . .
Из ранее рассмотренного материала известно, что реакцию цепи на короткий импульс можно считать равной произведению импульсной характеристики цепи на площадь импульсного воздействия. Следовательно, бесконечно малая составляющая реакции, обусловленная этим импульсным воздействием, в момент времени 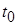 будет равной: будет равной:
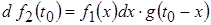 ,
,
поскольку площадь импульса равна 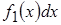 , а от момента его приложения , а от момента его приложения 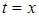 до момента наблюдения проходит время до момента наблюдения проходит время 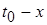 . .
Используя принцип наложения, полную реакцию цепи 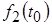 можно определить как сумму бесконечно большого числа бесконечно малых составляющих можно определить как сумму бесконечно большого числа бесконечно малых составляющих 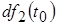 , вызванных последовательностью бесконечно малых по площади импульсных воздействий, предшествующих моменту времени , вызванных последовательностью бесконечно малых по площади импульсных воздействий, предшествующих моменту времени 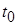 . .
Таким образом:
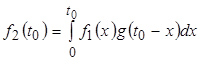 .
.
Эта формула верна для любых значений 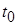 , поэтому обычно переменную , поэтому обычно переменную 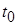 обозначают просто обозначают просто 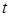 . Тогда: . Тогда:
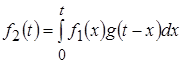 .
.
Полученное соотношение называют интегралом свертки или интегралом наложения. Функцию 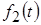 , которая находится в результате вычисления интеграла свертки, называют сверткой , которая находится в результате вычисления интеграла свертки, называют сверткой 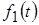 и и 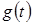 . .
Можно найти другую форму интеграла свертки, если в полученном выражении для 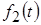 осуществить замену переменных: осуществить замену переменных:
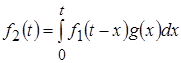 .
.
Пример: найти напряжение на емкости последовательной 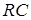 -цепи (рис. 8), если на входе действует экспоненциальный импульс вида: -цепи (рис. 8), если на входе действует экспоненциальный импульс вида:
 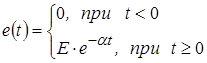
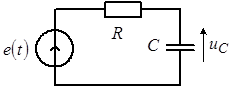
Рис. 8
Воспользуемся интегралом свертки:
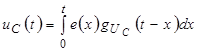 .
.
Выражение для 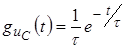 было получено ранее.
было получено ранее.
Следовательно, 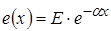 , и , и 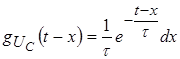 .
.
Тогда
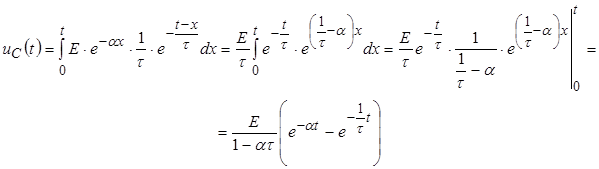
Такой же результат можно получить, применив интеграл Дюамеля.
Литература:
Белецкий А. Ф. Теория линейных электрических цепей. – М.: Радио и связь, 1986. (Учебник)
Бакалов В. П. и др. Теория электрических цепей. – М.: Радио и связь, 1998. (Учебник);
Качанов Н. С. и др. Линейные радиотехнические устройства. М.: Воен. издат., 1974. (Учебник);
Попов В. П. Основы теории цепей – М.: Высшая школа, 2000.(Учебник)
|