В.В. Сидоренков
МГТУ им. Н.Э. Баумана
Обсуждаются уравнения, структура и параметры реального электромагнитного поля состоящего из функционально связанных между собой четырех полевых векторных компонент: электрической и магнитной напряженностей, электрического и магнитного векторного потенциала, перемещающихся
в пространстве совместно посредством единого волнового процесса.
Считается, что все известные явления электромагнетизма обусловлены существованием и взаимодействием с материальными средами электромагнитного (ЭМ) поля, имеющего две векторные компоненты электрической 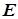 и магнитной и магнитной 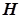 напряженности. При этом свойства этого поля физически полно и математически исчерпывающе описываются системой взаимосвязанных электродинамических уравнений, первоначальная форма и структура которых была сформулирована Максвеллом [1]. К сожалению, Максвелл ушел из жизни рано (в 48 лет), и свои гениальные уравнения он так и не успел привести в единую логическую систему. Поэтому при жизни его электродинамическая теория ЭМ поля не нашла должного признания в научной среде, более того, у большинства коллег отношение к ней было весьма оппозиционным, вплоть до полного неприятия: она считалась непонятной, математически нестрогой и логически необоснованной. Как отголоски прошлого и сегодня можно услышать разговоры о некоем примитивном «механическом» методе построения Максвеллом своих уравнений, хотя в явном виде в его главной работе [1] этого нет. Без преувеличения можно сказать, что для физика, инженера и преподавателя «Трактат об электричестве и магнетизме» Максвелла является бесценным информационным и методическим пособием, библией электромагнетизма, а для пытливого студента еще и физическими основами математического анализа. напряженности. При этом свойства этого поля физически полно и математически исчерпывающе описываются системой взаимосвязанных электродинамических уравнений, первоначальная форма и структура которых была сформулирована Максвеллом [1]. К сожалению, Максвелл ушел из жизни рано (в 48 лет), и свои гениальные уравнения он так и не успел привести в единую логическую систему. Поэтому при жизни его электродинамическая теория ЭМ поля не нашла должного признания в научной среде, более того, у большинства коллег отношение к ней было весьма оппозиционным, вплоть до полного неприятия: она считалась непонятной, математически нестрогой и логически необоснованной. Как отголоски прошлого и сегодня можно услышать разговоры о некоем примитивном «механическом» методе построения Максвеллом своих уравнений, хотя в явном виде в его главной работе [1] этого нет. Без преувеличения можно сказать, что для физика, инженера и преподавателя «Трактат об электричестве и магнетизме» Максвелла является бесценным информационным и методическим пособием, библией электромагнетизма, а для пытливого студента еще и физическими основами математического анализа.
Впоследствии, после триумфа теории Максвелла - открытия ЭМ волн (Герц, 1888 г.), первоначальная структура максвелловских уравнений была модернизирована Герцем, Хевисайдом и Эйнштейном, где новации заключались по существу лишь в уменьшении числа основных исходных уравнений. Но если говорить о положительном эффекте такой модификации, то их неоценимая заслуга состояла в методической и математической проработке этой теории. Предложенные «альтернативные» уравнения стали концептуально обозримы, логически более последовательны, имели удобный векторный вид и в определенной мере законченную форму, а в результате теория Максвелла приняла прозрачный в восприятии и современный при ее использовании вид.
В современном окончательном виде именно эту модернизированную систему уравнений:
(a) 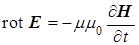 , (b) , (b) 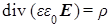 , (1) , (1)
(c) 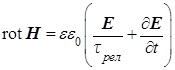 , (d) , (d) 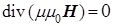
после ряда промежуточных названий и стали называть уравнениями Максвелла классической электродинамики [2]. Здесь 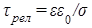 – постоянная времени релаксации электрического заряда в среде за счет ее электропроводности. – постоянная времени релаксации электрического заряда в среде за счет ее электропроводности.
Но в своем развитии научная мысль динамична, и вскоре наступило время возникновения, становления и бурного развития теории микромира, а потому основной научный интерес физиков был перенесен в эту новую, модную область изучения загадок Природы. В итоге после работ Максвелла развитием классической электродинамики физики по существу не занимались, но она перешла в руки инженеров, задача которых принципиально иная. Ведь психологически по образованию профессиональные интересы инженера не направлены на развитие физической науки, его цель – внедрение достижений этой науки в новых конкретных устройствах и разработка различных ее технических применений. По этой причине, несмотря на грандиозный технический прогресс, уже многие десятилетия классическая электродинамика и родственные ей науки находятся в концептуальном застое. Как бы тому иллюстрацией сегодня повсеместно с помпой категорически утверждается, что данная область физического знания наиболее полно разработана во всех ее аспектах и ее современный уровень является вершиной человеческого гения.
В этой связи попытаемся критически, но по возможности конструктивно проанализировать базовые основы классической электродинамики, которыми, по словам Герца, являются именно уравнения Максвелла. Как видим, эти уравнения рассматривают области пространства, где присутствует ЭМ поле, структурно реализуемое, согласно уравнениям (1а) и (1c), посредством динамически связанных между собой двух векторных взаимно ортогональных полевых компонент: электрической 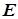 и магнитной и магнитной 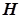 напряженности. Следующее уравнение (1b) описывает результат явления электрической поляризации в виде отклика материальной среды на наличие в данной точке стороннего электрического заряда ( напряженности. Следующее уравнение (1b) описывает результат явления электрической поляризации в виде отклика материальной среды на наличие в данной точке стороннего электрического заряда ( – объемная плотность стороннего заряда) либо на воздействие на среду внешнего электрического поля ( – объемная плотность стороннего заряда) либо на воздействие на среду внешнего электрического поля (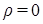 ). Соответственно, уравнение (1d) характеризует магнитную поляризацию. ). Соответственно, уравнение (1d) характеризует магнитную поляризацию.
Важнейшим фундаментальным следствием уравнений Максвелла служит тот факт, что компоненты ЭМ поля 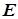 и и 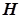 распространяются в пространстве в виде электродинамических волн. Например, из (1а) и (1c) получим волновое уравнение для поля электрической напряженности распространяются в пространстве в виде электродинамических волн. Например, из (1а) и (1c) получим волновое уравнение для поля электрической напряженности 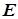 : :
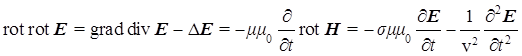 . .
Аналогично можно получить волновое уравнение для магнитной напряженности 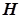 . Видно, что скорость распространения этих волн определяется только электрическими и магнитными параметрами пространства среды: . Видно, что скорость распространения этих волн определяется только электрическими и магнитными параметрами пространства среды: 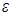 , , 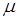 и и 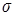 , в частности, в отсутствие поглощения ( , в частности, в отсутствие поглощения (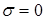 ) скорость ) скорость 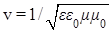 . .
С целью ответа на вопрос, какие это волны, и что они переносят, обратимся к закону сохранения энергии
, аналитическая формулировка которого непосредственно следует из уравнений Максвелла (1) в виде так называемой теоремы Пойнтинга:
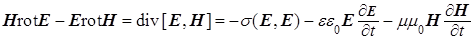 . (2) . (2)
Согласно (2), поступающий извне поток ЭМ энергии, определяемый вектором Пойнтинга 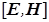 , идет на компенсацию в данной точке среды джоулевых (тепловых) потерь в процессе электропроводности и на изменение электрической и магнитной энергий, либо наоборот, указанные процессы вызывают излучение наружу потока ЭМ энергии. При этом реализующий энергетику данного процесса вектор Пойнтинга плотности потока ЭМ энергии , идет на компенсацию в данной точке среды джоулевых (тепловых) потерь в процессе электропроводности и на изменение электрической и магнитной энергий, либо наоборот, указанные процессы вызывают излучение наружу потока ЭМ энергии. При этом реализующий энергетику данного процесса вектор Пойнтинга плотности потока ЭМ энергии 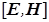 , связанный с вектором объемной плотности ЭМ импульса , связанный с вектором объемной плотности ЭМ импульса 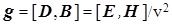 , отличен от нуля только там, где одновременно присутствуют электрическая и магнитная компоненты ЭМ поля, векторы , отличен от нуля только там, где одновременно присутствуют электрическая и магнитная компоненты ЭМ поля, векторы 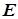 и и 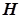 которых неколлинеарны. которых неколлинеарны.
Обсудим характеристики распространения ЭМ поля в виде плоской линейно поляризованной волны в однородной изотропной материальной среде. С точки зрения большей общности при анализе характеристик распространения указанного поля обычно значительно удобней использовать не волновые уравнения, а напрямую – сами уравнения системы (1), являющиеся по сути дела первичными уравнениями ЭМ волны. Для этого рассмотрим пакет указанной волны, распространяющийсявдоль оси x
с компонентами 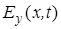 и и 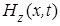 , которые представим комплексными спектральными интегралами: , которые представим комплексными спектральными интегралами:
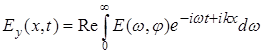 и и 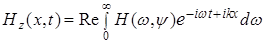 , ,
где 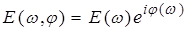 и и 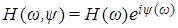 – комплексные амплитуды. Подставляя их в уравнения Максвелла (1a) и (1c), приходим к соотношениям – комплексные амплитуды. Подставляя их в уравнения Максвелла (1a) и (1c), приходим к соотношениям 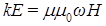 и и 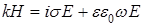 . В итоге получаем для уравнений системы (1) выражение: . В итоге получаем для уравнений системы (1) выражение: 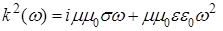 . .
В конкретном случае среды идеального диэлектрика (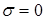 ) с учетом формулы ) с учетом формулы 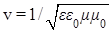 из из 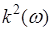 следует обычное дисперсионное соотношение следует обычное дисперсионное соотношение 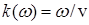 [2], описывающее однородные плоские волны ЭМ поля. При этом связь комплексных амплитуд в волновых решениях системы уравнений (1) представится в виде [2], описывающее однородные плоские волны ЭМ поля. При этом связь комплексных амплитуд в волновых решениях системы уравнений (1) представится в виде 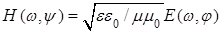 , а сами решения описывают волну, полевые компоненты , а сами решения описывают волну, полевые компоненты 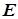 и и 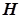 которой синфазно
( которой синфазно
(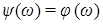 ) распространяются в пространстве. ) распространяются в пространстве.
Поскольку суть электромагнетизма – это взаимодействие ЭМ поля с материальной средой, то его анализ обычно сводится к стремлению описать энергетику ЭМ явлений. Обратимся и мы к соотношению энергетического баланса
(2), которое для среды идеального диэлектрика запишется в виде:
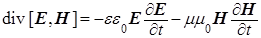 . (3) . (3)
Для анализа нам вполне достаточно рассмотреть, как выполняется выражение (3) для плоской монохроматической ЭМ волны, полевые компоненты которой, согласно волновым решениям уравнений Максвелла, в свободном пространстве без потерь при распространении совершают синфазные
колебания: 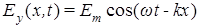 и и 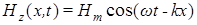 . Подставляя эти выражения в соотношение (3), окончательно получаем: . Подставляя эти выражения в соотношение (3), окончательно получаем:
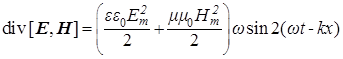 . (4) . (4)
Здесь весьма странно то, что, согласно 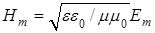 , равные по величине электрическая , равные по величине электрическая 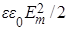 и магнитная и магнитная 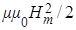 энергии хотя и распространяются совместно, но без видимой связи друг с другом. Кстати, в случае электро- и магнитостатики эти энергии в принципе раздельны и независимы. Таким образом, необходимо напрашивается вывод об объективности существования чисто электрической
и магнитной энергий
, при отсутствии каких-либо оснований считать, что распространение ЭМ волны реализуется посредством взаимной перекачки одной энергии в другую. Но тогда становится совершенно неясным, что же такое, казалось бы, очевидное для каждого понятие ЭМ энергии
, а также каков реальный механизм волнового переноса всех этих видов энергии. энергии хотя и распространяются совместно, но без видимой связи друг с другом. Кстати, в случае электро- и магнитостатики эти энергии в принципе раздельны и независимы. Таким образом, необходимо напрашивается вывод об объективности существования чисто электрической
и магнитной энергий
, при отсутствии каких-либо оснований считать, что распространение ЭМ волны реализуется посредством взаимной перекачки одной энергии в другую. Но тогда становится совершенно неясным, что же такое, казалось бы, очевидное для каждого понятие ЭМ энергии
, а также каков реальный механизм волнового переноса всех этих видов энергии.
Итак, решение уравнений электродинамики Максвелла для ЭМ волны не отвечает обычным физическим представлениям о распространении энергии посредством волн в виде процесса взаимного преобразования во времени в данной точке пространства энергии одной компоненты поля в энергию другой его компоненты. Следовательно, электродинамические уравнения (1) описывают необычную, весьма странную волну, которую логично назвать псевдоволной
, поскольку, с одной стороны, синфазные компоненты волны в принципе не способны переносить энергию, а с другой – перенос ЭМ энергии реально наблюдается, более того, это явление широко и всесторонне используется на практике, определяя многие аспекты жизни современного общества.
Таким образом, имеем парадокс, существующий, как это ни странно, уже более века. Поражает здесь то, что традиционная логика обсуждения переноса ЭМ энергии такова, что проблемы как бы и нет, всем все понятно. И действительно, из соотношения для амплитуд в волновых решениях уравнений системы (1) 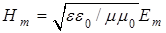 формально следует закон сохранения энергии формально следует закон сохранения энергии 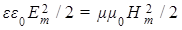 , хотя, как установлено выше, синфазные волны энергетически несостоятельны. Правда, изредка делаются попытки аргументировано разобраться в этом вопросе, но эти объяснения (например, [3]), на наш взгляд, не выдерживают критики, поскольку обсуждаются не сами уравнения Максвелла или их прямые следствия, а то, что эти уравнения не учитывают характеристики реальных ЭМ излучателей или некую специфику взаимодействия материальной среды с ЭМ полем. По мнению авторов, это и создает сдвиг фазы колебаний между компонентами на , хотя, как установлено выше, синфазные волны энергетически несостоятельны. Правда, изредка делаются попытки аргументировано разобраться в этом вопросе, но эти объяснения (например, [3]), на наш взгляд, не выдерживают критики, поскольку обсуждаются не сами уравнения Максвелла или их прямые следствия, а то, что эти уравнения не учитывают характеристики реальных ЭМ излучателей или некую специфику взаимодействия материальной среды с ЭМ полем. По мнению авторов, это и создает сдвиг фазы колебаний между компонентами на 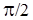 , реализующий перенос ЭМ энергии. , реализующий перенос ЭМ энергии.
В этой связи напомним основные физические представления о переносе энергии посредством волнового процесса, например, рассмотрим распространение волн от брошенного в воду камня. Частицы воды массой 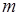 , поднятые на гребне волны на высоту , поднятые на гребне волны на высоту 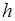 , имеют запас потенциальной энергии , имеют запас потенциальной энергии 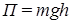 , а через четверть периода колебаний, когда гребень волны в данной точке пространства спадет, в соответствии с законом сохранения энергии
, потенциальная энергия частиц воды перейдет в кинетическую энергию их движения , а через четверть периода колебаний, когда гребень волны в данной точке пространства спадет, в соответствии с законом сохранения энергии
, потенциальная энергия частиц воды перейдет в кинетическую энергию их движения 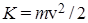 , где скорость частиц , где скорость частиц 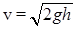 . Наличие взаимодействия молекул воды и приводит к возбуждению механической поверхностной поперечной волны, которая переносит в волновом процессе механическую энергию так, что . Наличие взаимодействия молекул воды и приводит к возбуждению механической поверхностной поперечной волны, которая переносит в волновом процессе механическую энергию так, что 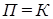 . Физически логично считать, что механизм переноса энергии ЭМ волнами в главном должен быть аналогичен, как и у других волн иной физической природы, возможно обладая при этом, исходя из структуры электродинамических уравнений Максвелла (1), определенной спецификой и даже уникальностью. . Физически логично считать, что механизм переноса энергии ЭМ волнами в главном должен быть аналогичен, как и у других волн иной физической природы, возможно обладая при этом, исходя из структуры электродинамических уравнений Максвелла (1), определенной спецификой и даже уникальностью.
Для большей убедительности наших аргументов чисто формально рассмотрим энергетику распространения некой гипотетической
ЭМ волны
, у которой имеется сдвиг фазы колебаний между ее полевыми компонентами на 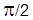 : : 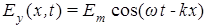 и и 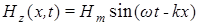 . Очевидно, что подставлять эти компоненты в соотношение (3) не имеет смысла, поскольку, согласно уравнениям Максвелла, теоремы Пойнтинга (2) для них нет, соответственно и такие волновые решения никак не следуют из уравнений (1). И все же вычислим для такой ЭМ волны объемную плотность потока вектора Пойнтинга. Тогда с учетом . Очевидно, что подставлять эти компоненты в соотношение (3) не имеет смысла, поскольку, согласно уравнениям Максвелла, теоремы Пойнтинга (2) для них нет, соответственно и такие волновые решения никак не следуют из уравнений (1). И все же вычислим для такой ЭМ волны объемную плотность потока вектора Пойнтинга. Тогда с учетом 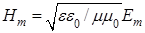 и и 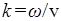 (где (где 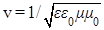 ) чисто математически получим ) чисто математически получим
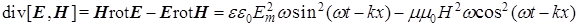
Усредняя это выражение по времени (по периоду колебаний), имеем 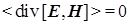 , то есть мы приходим здесь к физически разумному результату, когда посредством обсуждаемой гипотетической волны
в пространстве без потерь переносится энергия , то есть мы приходим здесь к физически разумному результату, когда посредством обсуждаемой гипотетической волны
в пространстве без потерь переносится энергия 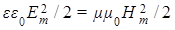 , не зависящая от времени и точек пространства. Следовательно, при таком волновом процессе, как и ожидалось, имеем выполнение закона сохранения энергии
. К сожалению, мы убедились выше, что это невозможно в принципе, поскольку, согласно уравнениям Максвелла, ЭМ волн с такими характеристиками в Природе нет. , не зависящая от времени и точек пространства. Следовательно, при таком волновом процессе, как и ожидалось, имеем выполнение закона сохранения энергии
. К сожалению, мы убедились выше, что это невозможно в принципе, поскольку, согласно уравнениям Максвелла, ЭМ волн с такими характеристиками в Природе нет.
Итак, проблема с выяснением механизма переноса энергии волнами ЭМ поля объективно существует, и для ее разрешения требуется, по всей видимости, весьма нестандартный эвристический подход. Но в наличии у нас имеется только система уравнений электродинамики Максвелла, а потому для разрешения обсуждаемого здесь парадокса ничего не остается, как продолжить критический анализ именно уравнений (1) с целью поиска новых (скрытых) реалий в их физическом содержании. И действительно, такие реалии в указанных уравнениях были обнаружены [4], а их суть заключена в соотношениях исходной первичной взаимосвязи ЭМ поля
с компонентами электрической 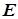 и магнитной и магнитной 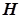 напряженности и поля ЭМ векторного потенциала
с электрической напряженности и поля ЭМ векторного потенциала
с электрической 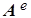 и магнитной и магнитной 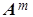 компонентами: компонентами:
(a) 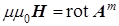 , (c) , (c) 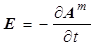 , (e) , (e) 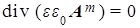 , (5) , (5)
(b) 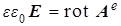 , (d) , (d) 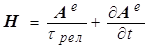 , (g) , (g) 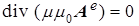 . .
Здесь соотношение (5a) вводится с помощью уравнения (1d), поскольку дивергенция ротора произвольного векторного поля тождественно равна нулю. Соответственно, (5b) следует из уравнения (1b) при 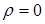 , справедливого для сред с локальной электронейтральностью. Далее подстановка (5a) в (1а) дает (5c), а подстановка (5b) в (1c) приводит к (5d). Чисто вихревой характер компонент векторного потенциала , справедливого для сред с локальной электронейтральностью. Далее подстановка (5a) в (1а) дает (5c), а подстановка (5b) в (1c) приводит к (5d). Чисто вихревой характер компонент векторного потенциала 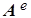 и и 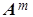 обеспечивается дивергентными уравнениями (5e) и (5g) кулоновской калибровки, однако физически они описывают отклик материальной среды на наличие в ней поля ЭМ векторного потенциала. обеспечивается дивергентными уравнениями (5e) и (5g) кулоновской калибровки, однако физически они описывают отклик материальной среды на наличие в ней поля ЭМ векторного потенциала.
Как видим, объединение соотношений в систему (5) оказалось весьма конструктивным, так как в этом случае возникает система дифференциальных уравнений, описывающих значительно более сложное и необычное с точки зрения общепринятых воззрений вихревое векторное поле
в виде совокупности функционально связанных между собой четырех вихрево-полевых компонент 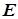 , , 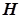 и и 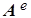 , , 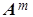 , которое логично назвать реальным электромагнитным полем
. , которое логично назвать реальным электромагнитным полем
.
Объективность существования такого электродинамического
поля
иллюстрируется нетривиальными следствиями из полученных выше соотношений, поскольку подстановки (5c) в (5b) и (5d) в (5a) приводят к системе новых электродинамических уравнений, структурно полностью аналогичной системе традиционных уравнений Максвелла (1), но уже для поля ЭМ векторного потенциала
с электрической 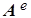 и магнитной и магнитной 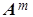 компонентами: компонентами:
(a) 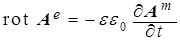 , (b) , (b) 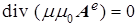 , (6) , (6)
(c) 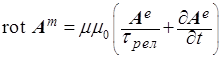 , (d) , (d) 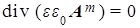 . .
Чисто вихревой характер компонент поля векторного потенциала обеспечивается условием кулоновской калибровки посредством дивергентных уравнений (6b) и (6d), которые при этом представляют собой начальные условия в математической задаче Коши для уравнений (6a) и (6c), что делает эту систему уравнений замкнутой.
Соответственно, математические операции с соотношениями (5) позволяют получить [4] еще две других системы уравнений:
для электрического поля
с компонентами 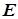 и и 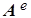
(a) 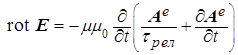 , (b) , (b) 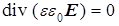 , (7) , (7)
(c) 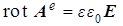 , (d) , (d) 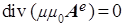
и для магнитного поля
с компонентами 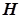 и и 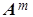 : :
(a) 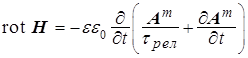 , (b) , (b) 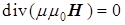 , (8) , (8)
(c) 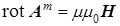 , (d , (d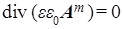
Поскольку соотношения системы (5) можно получить независимо посредством действия векторного оператора набла
и временной производной
в пространстве поля компонент 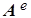 и и 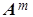 векторного потенциала, то из них подобно системам (6) – (8) следуют и уравнения Максвелла (1), справедливые для локально электронейтральных сред ( векторного потенциала, то из них подобно системам (6) – (8) следуют и уравнения Максвелла (1), справедливые для локально электронейтральных сред (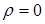 ). ).
Таким образом, уравнения (5) первичной исходной взаимосвязикомпонент ЭМ поля и поля ЭМ векторного потенциала, безусловно, фундаментальны и объективно являются основными уравнениями современной полевой теории электромагнетизма.
Далее, как и следовало ожидать, из этих новых систем электродинамических уравнений непосредственно получаем (аналогично выводу формулы (2)) соотношения баланса:
судя по размерности, для потока момента ЭМ импульса
из уравнений (6)
 (9)
(9)
для потока электрической энергии
из уравнений (7)
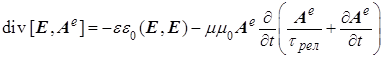 .
(10)
.
(10)
и, наконец, для потока магнитной энергии
из уравнений (8)
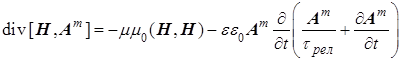 .(11)
.(11)
Все это действительно подтверждает и объективно доказывает, что, наряду с ЭМ полем
с векторными компонентами 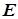 и и 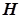 , в Природе существуют и другие поля: поле ЭМ векторного потенциала
с компонентами , в Природе существуют и другие поля: поле ЭМ векторного потенциала
с компонентами 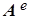 и и 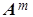 ,
электрическое поле
с компонентами ,
электрическое поле
с компонентами 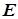 и и 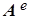 , магнитное поле
с , магнитное поле
с 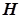 и и 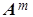 . Таким образом, структура из двух векторных взаимно ортогональных компонент реализует способ существования конкретного электродинамического поля, делает принципиально возможным его перемещение в пространстве в виде потока соответствующей физической величины. . Таким образом, структура из двух векторных взаимно ортогональных компонент реализует способ существования конкретного электродинамического поля, делает принципиально возможным его перемещение в пространстве в виде потока соответствующей физической величины.
Можно убедиться, следуя логике рассуждений вывода волнового уравнения для поля вектора электрической напряженности 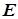 , что форма и структура представленных систем уравнений (1), (6) - (8) говорят о существовании волновых решений для всех четырех компонент реального электромагнитного поля
. Тем самым описываются волны конкретных вышеперечисленных двухкомпонентных полей посредством одной из парных комбинаций четырех указанных волновых уравнений. В итоге возникает очевидный вопрос: что это за волны, и каковы характеристики их распространения? , что форма и структура представленных систем уравнений (1), (6) - (8) говорят о существовании волновых решений для всех четырех компонент реального электромагнитного поля
. Тем самым описываются волны конкретных вышеперечисленных двухкомпонентных полей посредством одной из парных комбинаций четырех указанных волновых уравнений. В итоге возникает очевидный вопрос: что это за волны, и каковы характеристики их распространения?
Поскольку структурная симметрия уравнений систем (1) и (6) математически тождественна, а волновые решения уравнений (1) выше уже проанализированы, то далее анализ условий распространения плоских электродинамических волн в однородных изотропных материальных средах проведем, прежде всего, для уравнений систем (7) и (8). Их необычные структуры между собой также тождественны, а волновые решения уравнений в литературе не рассматривались.
Итак, рассмотрим волновой пакет плоской линейно поляризованной электрической волны
с компонентами 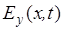 и и 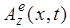 для системы (7) либо магнитной волны
с компонентами для системы (7) либо магнитной волны
с компонентами 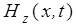 и и 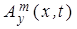 для системы (8), которые представим комплексными спектральными интегралами. Тогда, проводя аналогичные рассуждения, как и для рассматриваемого выше пакета плоской ЭМ волны, получим соотношения для волны электрического поля для системы (8), которые представим комплексными спектральными интегралами. Тогда, проводя аналогичные рассуждения, как и для рассматриваемого выше пакета плоской ЭМ волны, получим соотношения для волны электрического поля
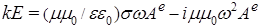 и и 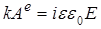 . Соответственно, для магнитного поля . Соответственно, для магнитного поля
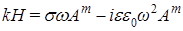 и и 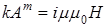 . Таким образом, для систем уравнений (7) и (8) имеем общее выражение: . Таким образом, для систем уравнений (7) и (8) имеем общее выражение:  . .
В конкретном случае среды идеального диэлектрика (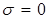 ) из ) из 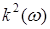 с учетом формулы с учетом формулы 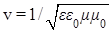 следует обычное дисперсионное соотношение следует обычное дисперсионное соотношение 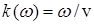 [2], описывающее однородные плоские волны электрического или магнитного полей. При этом связь комплексных амплитуд компонент указанных волновых полей имеет специфический вид: [2], описывающее однородные плоские волны электрического или магнитного полей. При этом связь комплексных амплитуд компонент указанных волновых полей имеет специфический вид:
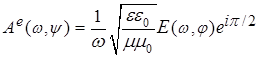 и и 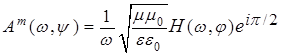 . .
Главная специфика здесь состоит в том, что при распространении в диэлектрической среде компоненты поля сдвинуты между собой по фазе на 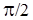 , то есть характер поведения компонент поля таких волн в любой точке пространства аналогичен кинематическим параметрам движения (смещение и скорость) классической частицы в точке устойчивого равновесия поля потенциальных сил. Конечно, данный результат математически тривиален, поскольку компоненты ЭМ поля и поля ЭМ векторного потенциала связаны между собой посредством производной по времени (см. соотношения (5)). Однако концептуально, с физической точки зрения такой факт примечателен и требует анализа. , то есть характер поведения компонент поля таких волн в любой точке пространства аналогичен кинематическим параметрам движения (смещение и скорость) классической частицы в точке устойчивого равновесия поля потенциальных сил. Конечно, данный результат математически тривиален, поскольку компоненты ЭМ поля и поля ЭМ векторного потенциала связаны между собой посредством производной по времени (см. соотношения (5)). Однако концептуально, с физической точки зрения такой факт примечателен и требует анализа.
Справедливости ради здесь уместно сказать, что впервые о реальности магнитной поперечной волны
с двумя ее компонентами 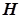 и и 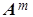 , сдвинутыми при распространении по фазе колебаний на , сдвинутыми при распространении по фазе колебаний на 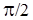 , еще в 1980 году официально заявил в виде приоритета на открытие Докторович [6], и свое достижение он с удивительным упорством, достойным лучшего применения, безуспешно пытается донести до других все эти долгие годы. Весьма печально, ибо только Время – высший судья, и именно оно расставит все и всех по своим местам! , еще в 1980 году официально заявил в виде приоритета на открытие Докторович [6], и свое достижение он с удивительным упорством, достойным лучшего применения, безуспешно пытается донести до других все эти долгие годы. Весьма печально, ибо только Время – высший судья, и именно оно расставит все и всех по своим местам!
Аналогичные рассуждения для пакета плоской волны векторного потенциала
с компонентами 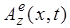 и и 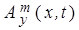 в системе (6) дают в системе (6) дают 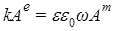 и и 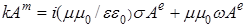 , откуда снова получаем известное выражение , откуда снова получаем известное выражение 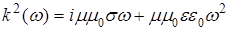 . А потому для среды диэлектрика ( . А потому для среды диэлектрика (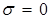 ) дисперсионное соотношение для уравнений (6) будет ) дисперсионное соотношение для уравнений (6) будет 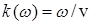 при комплексных амплитудах в волновых решениях: при комплексных амплитудах в волновых решениях: 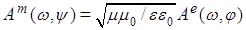 , где сами решения описывают плоские однородные волны, компоненты поля которых, как и в случае ЭМ волн, синфазно
распространяются в пространстве. , где сами решения описывают плоские однородные волны, компоненты поля которых, как и в случае ЭМ волн, синфазно
распространяются в пространстве.
Как видим, именно уравнения поля ЭМ векторного потенциала
(6) описывают перенос в пространстве потока момента импульса
, который со времен Пойнтинга пытаются описать с помощью уравнений ЭМ поля (1) (см. анализ в [6]). В этой связи укажем на пионерские работы [7], где обсуждается неэнергетическое (информационное) взаимодействие векторного потенциала со средой при передаче в ней потенциальных волн и их детектирование с помощью эффекта, аналогичного эффекту Ааронова-Бома.
Здесь важно отметить, что система уравнений (5) иллюстрирует тот непреложный факт, что динамическое
существование поля ЭМ векторного потенциала сопровождается неразрывно сопутствующим ему традиционным ЭМ полем. Причем, как установлено, перенос компонентами этих двух полей потока соответствующей физической величины существует, но не посредством обычного волнового процесса, который принципиально невозможен, но он реализуется опосредованно в виде так называемых псевдоволн
.
Согласно проведенному здесь анализу, для проводящей среды в асимптотике металлов (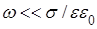 ) распространение волн всех четырех электродинамических составляющих реального ЭМ поля
подчиняется теоретически хорошо изученному закону для волн “обычного” ЭМ поля в металлах [2], где все волновые решения имеют вид экспоненциально затухающих в пространстве плоских волн со сдвигом фазы между компонентами на ) распространение волн всех четырех электродинамических составляющих реального ЭМ поля
подчиняется теоретически хорошо изученному закону для волн “обычного” ЭМ поля в металлах [2], где все волновые решения имеют вид экспоненциально затухающих в пространстве плоских волн со сдвигом фазы между компонентами на 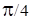 . .
Однако вернемся к обсуждению энергетики распространения составляющих реального электромагнитного поля
в виде плоских волн в диэлектрической среде без потерь (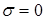 ). Вначале обратимся к закону сохранения электрической энергии
, соотношение которого согласно (10) запишется как: ). Вначале обратимся к закону сохранения электрической энергии
, соотношение которого согласно (10) запишется как:
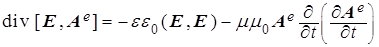 .(12)
.(12)
Выясним, что представляет собой это выражение для энергии монохроматической электрической волны
, полевые компоненты которой, согласно волновым решениям уравнений системы (7), обладая сдвигом фазы на 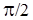 , имеют следующий вид: , имеют следующий вид: 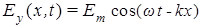 и и 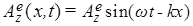 . Тогда, подставляя их в соотношение (12), приходим к соотношению: . Тогда, подставляя их в соотношение (12), приходим к соотношению:
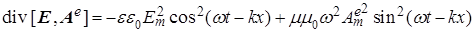 .
.
Такой результат вполне удовлетворяет закону сохранения энергии
, поскольку усреднение по времени этого соотношения дает
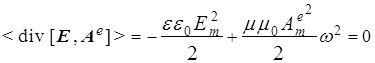 , (13)
, (13)
а потому электрической волной
переносится чисто электрическая энергия
: 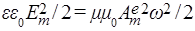 , не зависящая от времени и точек пространства. , не зависящая от времени и точек пространства.
Соответственно, для магнитного поля
, распространяющегося в среде без потерь, уравнение энергетического баланса
(11) запишется в виде:
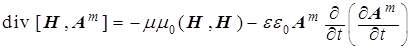 .(14)
.(14)
Рассмотрим, как выполняется этот закон для плоской монохроматической магнитной волны
, полевые компоненты которой, согласно волновым решениям уравнений (8), имеют вид: 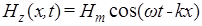 и и 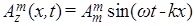 . Подставляя их в соотношение (14) и проводя аналогичные рассуждения как при выводе формулы (13), получаем в итоге: . Подставляя их в соотношение (14) и проводя аналогичные рассуждения как при выводе формулы (13), получаем в итоге:
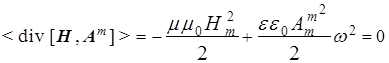 . (15)
. (15)
Итак, в случае магнитного поля
снова приходим к физически здравому результату, когда в пространстве без потерь посредством магнитной волны
переносится чисто магнитная энергия 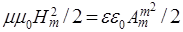 , не зависящая от времени и точек пространства. Следовательно, распространение магнитной волны
также удовлетворяет закону сохранения энергии
. , не зависящая от времени и точек пространства. Следовательно, распространение магнитной волны
также удовлетворяет закону сохранения энергии
.
Таким образом, аргументированно показано, что в Природе объективно существует весьма сложное и необычное с точки зрения традиционных представлений вихревое четырехвекторное поле
в виде совокупности функционально связанных между собой четырех вихрево-полевых компонент 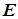 , , 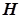 и и 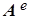 , ,
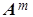 . Это поле, названное реальным электромагнитным полем
, реализуется четверкой составляющих его электродинамических полей, состоящих из пар вышеуказанных компонент: электрическое поле
с . Это поле, названное реальным электромагнитным полем
, реализуется четверкой составляющих его электродинамических полей, состоящих из пар вышеуказанных компонент: электрическое поле
с 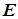 и и 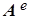 , магнитное поле
с , магнитное поле
с 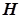 и и 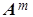 , электромагнитное поле
с , электромагнитное поле
с 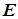 и и 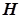 , наконец, поле векторного потенциала
с , наконец, поле векторного потенциала
с 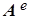 и и 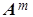 . При этом описывающие эти поля электродинамические уравнения (5) являются основными уравнениями современной полевой теории электромагнетизма
, которые с их следствиями: системами уравнений (1) и (6) - (8) представляют собой фундамент классической электродинамики. . При этом описывающие эти поля электродинамические уравнения (5) являются основными уравнениями современной полевой теории электромагнетизма
, которые с их следствиями: системами уравнений (1) и (6) - (8) представляют собой фундамент классической электродинамики.
Установлено, что способностью к непосредственному распространению в пространстве в виде волн, отвечающих обычным физическим представлениям о волновом процессе, обладают только волны электрического
и магнитного полей
за счет наличия у них сдвига фазы колебаний на 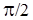 между их компонентами между их компонентами 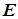 и и 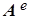 , соответственно, , соответственно, 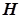 и и 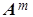 . Реализация же собственно волн ЭМ поля
и ЭМ векторного потенциала
невозможна в принципе, хотя сами эти поля и их потоки безусловно существуют, но распространяются они опосредованно в виде псевдоволн
, поскольку их синфазные
компоненты . Реализация же собственно волн ЭМ поля
и ЭМ векторного потенциала
невозможна в принципе, хотя сами эти поля и их потоки безусловно существуют, но распространяются они опосредованно в виде псевдоволн
, поскольку их синфазные
компоненты 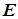 и и 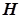 , соответственно, , соответственно, 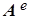 и и 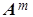 являются составной частью компонент электрической и магнитной волн.
Именно тем самым все составляющие реального ЭМ поля
перемещаются в пространстве совместно посредством единого волнового процесса. являются составной частью компонент электрической и магнитной волн.
Именно тем самым все составляющие реального ЭМ поля
перемещаются в пространстве совместно посредством единого волнового процесса.
Однако современными методами регистрации электродинамических полей наблюдают только псевдоволны
“обычного” ЭМ поля, компоненты 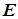 и и 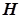 которых синфазно распространяются в пространстве. И хотя конкретное изучение волн остальных обсуждаемых здесь составляющих реального электромагнитного поля
только начинается (например, в [8] представлены результаты экспериментального исследования условий возбуждения и распространения в металлах поперечных чисто магнитных волн), объективность их существования и неоспоримая практическая значимость подтверждается, например, принципиальной невозможностью без их посредства реализации такой столь важной физической характеристики ЭМ поля, как способности переноса его энергии. которых синфазно распространяются в пространстве. И хотя конкретное изучение волн остальных обсуждаемых здесь составляющих реального электромагнитного поля
только начинается (например, в [8] представлены результаты экспериментального исследования условий возбуждения и распространения в металлах поперечных чисто магнитных волн), объективность их существования и неоспоримая практическая значимость подтверждается, например, принципиальной невозможностью без их посредства реализации такой столь важной физической характеристики ЭМ поля, как способности переноса его энергии.
Как видим, застарелый, возрастом более века парадокс существования волн ЭМ поля и переноса ими энергии этого поля, наконец, успешно и весьма нетривиально разрешен, а результаты проведенных исследований представляют собой серьезное концептуальное развитие основных физических воззрений на структуру и свойства ЭМ поля в классической электродинамике. Кстати, методически серьезных проблем не должно возникнуть, если обсуждаемое здесь реальное электромагнитное поле
сохранит за собойи традиционное в электромагнетизменынешнее название –
электромагнитное
поле
с учетом современного развития физических воззрений и его нового содержания. Также с методической точки зрения следует отметить, что настоящий материал вместе с результатами работ [4] может служить концептуальной базой модернизации учебных курсов и создания новых пособий по общей физике, классической электродинамике и родственным им техническим дисциплинам.
Литература
1. Максвелл Дж. К.
Трактат об электричестве и магнетизме. Т. I и II. М.: Наука, 1989.
2. Матвеев А.Н.
Электродинамика. М.: Высшая школа, 1980.
3. Пирогов А.А.
// Электросвязь. 1993. №5. С. 13-14.
4. Сидоренков В.В.
// Труды X Всероссийской школы-семинара «Физика и применение микроволн». Секция 2. “Электродинамика”. - М.: МГУ, 2005. С. 2-7; // Необратимые процессы в природе и технике: Сборник научных работ. Выпуск I. - М.: МГТУ им. Н.Э. Баумана, 2005. - С. 127-138; // Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2006. № 1. С. 28-37; // Материалы IX Международной конференции «Физика в системе современного образования». Санкт-Петербург: РГПУ, 2007. Секция 1. “Профессиональное физическое образование”. С. 127-129; // Вестник Воронежского государственного технического университета. 2007. Т. 3. № 11. С. 75-82.
5. Докторович З.И.
// Заявленное открытие "Магнитные поперечные волны" приоритетная справка 32-ОТ №10247, дата поступления 5 мая 1980 г.
6. Соколов И.В.
//УФН. 1991. Т. 161.№ 10. С. 175-190.
7. Чирков А.Г., Агеев А.Н.
// ФТТ. 2002. Т. 44. Вып. 1. С. 3-5; 2007. Т. 49. Вып. 7. С. 1217-1221.
8. Сидоренков В.В.
// Труды V Всероссийской конференции «Необратимые процессы в природе и технике». Часть I. - М.: МГТУ им. Н.Э. Баумана, 2009. - С. 166-170.
|