Академия
Кафедра Физики
Реферат
Условия фильтрации для реактивных лестничных четырехполюсников
Орёл 2009
Содержание
Назначение и классификация электрических фильтров
Свойства реактивных двухполюсников
Условия фильтрации для реактивных четырехполюсников
Заключение
Литература
Назначение и классификация электрических фильтров
Электрическим фильтром называют четырехполюсник, предназначенный для выделения из состава сложного электрического колебания частотных составляющих, расположенных в заданной полосе частот, и подавления тех составляющих, которые расположены в других, также заданных, полосах частот.
Указанные полосы называют соответственно полосой пропускания (ПП) и полосой задерживания (ПЗ) фильтра. По взаимному расположению ПП и ПЗ фильтры классифицируются следующим образом:
• фильтры нижних частот (ФНЧ)
• фильтры верхних частот(ФВЧ)
• полосовые фильтры (ПФ)
• режекторные фильтры (РФ)
Требования к АЧХ формулируются обычно в виде требований к частотной зависимости затухания (ослабления). При этом неравномерность затухания фильтра в его полосе пропускания не должна превышать некоторой величины Δа, а в пределах полосы задерживания фильтра затухание не должно принимать значений меньших, чем это допускается техническими требованиями. На рисунке 1 в качестве примера показаны требования к характеристике затухания. Здесь же изображена полоса перехода, в которой затухание не нормируется.

Рис.1
Пунктирной линией показан один из вариантов реального затухания ФНЧ, удовлетворяющего заданным требованиям.
Помимо требований к затуханию фильтра могут предъявляться и другие.
Классификация электрических фильтров может быть осуществлена также по элементной базе:
• LC фильтры;
• кварцевые и пьезокерамические фильтры;
• электромеханические и магнитострикционные фильтры;
• фильтры на поверхностных акустических волнах;
• RC и ARC -фильтры;
• цифровые фильтры и т.д.
По виду характеристики затухания (или АЧХ) различают фильтры с максимально-плоскими характеристиками, с равноволновыми характеристиками и фильтры со всплесками затухания.
Приведенная классификация не является исчерпывающей. Например, в технике многоканальной связи фильтры могут классифицировать по назначению: канальные, фильтры групп каналов, линейные фильтры и т.д.
Прежде чем перейти к анализу и синтезу электрических фильтров, рассмотрим свойства реактивных двухполюсников, которые являются составными элементами LC -фильтров".
Свойства реактивных двухполюсников
Реактивным двухполюсником (РД) называют электрическую цепь с двумя зажимами, состоящую из чисто реактивных элементов (индуктивностей и емкостей).
Такие двухполюсники не имеют потерь (активная составляющая сопротивления равна 0) и сопротивление их чисто реактивное. Свойства РД удобно оценивать по характеру изменения его реактивного сопротивления от частоты.
Важное значение в этом случае имеют некоторые частоты, при которых сопротивление РД обращается в нуль или стремится к бесконечно большой величине.
Частоты, при которых сопротивление РД обращается в нуль получили название нулей сопротивлений. Частоты, при которых сопротивление РД стремится к бесконечно большой величине получили название полюсов сопротивлений.
Условное расположение нулей (0) и полюсов (х) на оси частот принято называть характеристической строкой РД.
Рассмотрим характеристики простейших РД.
Сопротивление РД имеет: Сопротивление РД имеет:
нуль при ω=0 и полюс при ω=0 и
полюс при ω→ нуль при ω→ нуль при ω→
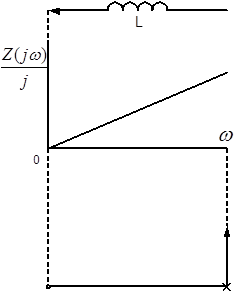 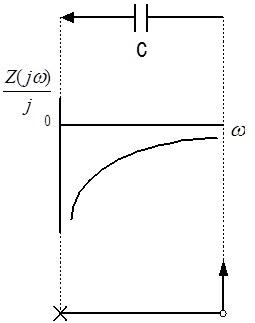
Более сложные РД получаются при последовательном или параллельном соединении простейших.
Так, соединяя последовательно L и С получим двухполюсник:График частотной зависимости сопротивления РД и характеристическая строка имеют вид:

Таким образом рассматриваемый РД имеет два полюса сопротивления: при ω=0 и ω→ и один нуль: при ω=ω1 и один нуль: при ω=ω1
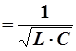

График частотной зависимости сопротивления и характеристическая строка двухполюсника, состоящего из параллельно соединенных элементов LC имеет вид
: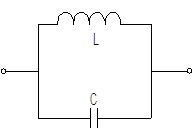 
Как видно, РД имеет два нуля сопротивления: при ω=0 и ω= и один полюс: при и один полюс: при
ω=ω1
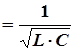

Отметим, что на частоте резонанса (ω=ω1
) происходит изменение характера реактивности двухполюсника с емкостного на индуктивный при последовательном соединении и с индуктивного на емкостной при параллельном соединении элементов.
У более сложных РД характер реактивности с ростом частоты может изменяться не один, а несколько раз.
Подобным же образом можно рассмотреть и более сложные РД и сформулировать общие правила анализа. Например, в 3-х элементном РД
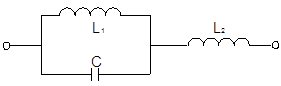
Сначала наступает резонанс токов, обусловленный элементами L1
и C, а затем резонанс напряжений за счет элемента L2
и эквивалентной емкости контура L1
C после его резонансной частоты:

Общие правила анализа РД:
1. Число нулей и полюсов сопротивления РД, расположенных при конечных значениях частоты, равно числу элементов L и С.
2. Нули и полюсы сопротивления РД чередуются, при этом всякий раз меняется характер реактивности.
3. Если в РД есть путь для постоянного тока, то характеристическая строка начинается с нуля, а в противном случае характеристическая строка начинается с полюса.
Зная общие правила анализа можно решить две задачи:
1. Для заданной схемы РД построить характеристическую строку и частотную зависимость его сопротивления (задача анализа).
2. Построить РД, удовлетворяющий заданным требованиям частотной зависимости и его сопротивления (задача синтеза).
Отметим, что одну и ту же характеристическую строку можно реализовать разными по структуре РД, которые в данном случае принято называть эквивалентными.
РД являются составными частями LC -фильтров, подавляющее большинство которых в аппаратуре связи имеет лестничную структуру.
Реактивный четырехполюсник называют лестничным, если образующие его РД поочередно включаются в продольные и поперечные ветви схемы.
Лестничные четырехполюсники образуют из Т- и П- образных четырехполюсников путем каскадного согласованного соединения их. Последние же получают путем соединения элементарных Г- образных полузвеньев Т- или П- образными сторонами, как показано на рисунках:
 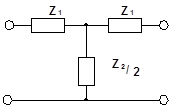 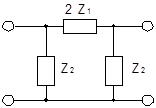
Г - образное Симметричное Симметричное полузвено Т - образное звено П - образное звено
Рассмотрим условия фильтрации для Г- образного полузвена.
Условия фильтрации для реактивных четырехполюсников
Определим условия, при которых реактивный четырехполюсник (четырехполюсник без потерь) будет электрическим фильтром, т.е. устройством, имеющим в некоторой области частот полосу пропускания, а в другой - полосу задерживания.
Условия фильтрации (УФ) найдем для четырехполюсника в виде элементарного Г- образного полузвена, а затем распространим их на каскадное соединение, т.е. на Т- и П- образные звенья.
Ранее было получено соотношение, связывающее характеристическое затухание с параметрами XX и КЗ.
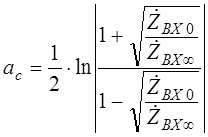 (1) (1)
Для Г- образного полузвена найдем:
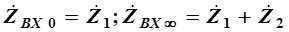
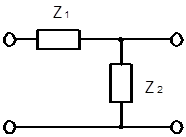
С учетом этого можно записать выражение для характеристического затухания Г- образного полузвена:
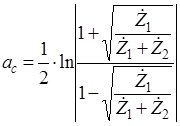 (1) (1)
Как видно из формулы, характеристическое затухание зависит от соотношения сопротивлений продольной и поперечной ветвей четырехполюсника. Условились характеристической ПП считать область частот, где характеристическое затухание равно нулю.
Следовательно, в области частот, в которой модуль выражения (1) равен 1, ln=0 и фильтр имеет ПП. При всех же других частотах ac
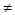 0 т.е. расположена ПЗ. 0 т.е. расположена ПЗ.
Не трудно заметить, что модуль выражения (1) равен 1 в двух случаях:
а) при 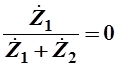 б) при б) при 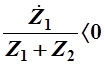 
Если обозначить 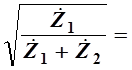 jA то jA то
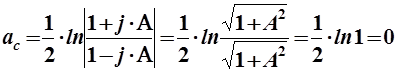
Таким образом, ПП реактивного четырехполюсника расположена на частотах, на которых справедливо неравенство
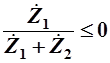 ; ; 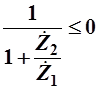 ; ; 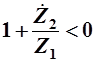 ; ; 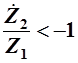 ; ;
Видно, что данное неравенство имеет место при выполнении двух условий:
1. 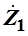 и и 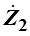 должны иметь разные знаки; должны иметь разные знаки;
2. 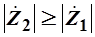 
Фактически это и есть условие фильтрации (т.е. условие получения ПП) для реактивного Г- образного полузвена.
При составлении звеньев и более сложных фильтров из Г- образных полузвеньев, имеющих одинаковую частоту среза, затухание суммируется, следовательно условия фильтрации определяются Г- образным полузвеном.
Рассмотрим примеры применения УФ:
1) Данный четырехполюсник - ФНЧ.
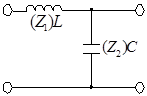 
Из графика видно, что условия фильтрации выполняются в полосе частот (0,ω0
) поэтому данный четырехполюсник является ФНЧ.
Если L и С поменять местами, то нетрудно убедиться, что четырехполюсник будет ФВЧ.
2) Данный четырехполюсник - ПФ.
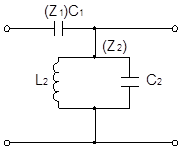 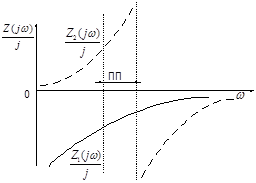
Определим условия фильтрации для мостового реактивного четырехполюсника.
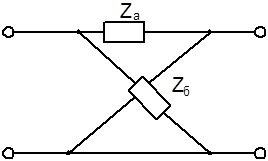
Ранее мы установили, что ХПП лежит в области частот, где

В данном случае
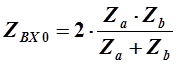 и и 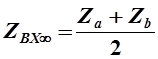 откуда откуда

Полученное выражение будет отрицательным при противоположных знаках Za
и Zb
.
Таким образом ХПП для мостового симметричного четырехполюсника лежит в области частот, где Za
и Zb
имеют противоположные знаки.
Укажем, что мостовые звенья используются при построении фазовых корреляторов, кварцевых фильтров и других устройств.
Заключение
Отметить, что использование характеристических параметров для получения условий фильтрации дает возможность сравнительно легко определить тип фильтра и примерное расположение полос пропускания и задержания. Однако расчет фильтра по характеристическим параметрам является не оптимальным и не обладает должной гибкостью. Поэтому на практике все более широкое применение находят так называемые методы синтеза электрических фильтров по их рабочим параметрам, что и будет продемонстрировано в следующих лекциях.
Литература
1. Белецкий А.Ф. «Теория линейных электрических цепей » Москва 1986 с 368-383
2. Белецкий А.Ф. «Линейные устройства аппаратуры связи. Конспект лекций»
3. Бакалов В.П. «Теория электрических цепей» Москва «Радио и связь» 1998- с.368-390
|