Федеральное агентство по образованию РФ.
Государственное образовательное учреждение высшего профессионального образования
Забайкальский государственный гуманитарно-педагогический университет им. Н. Г. Чернышевского.
Физико-математический факультет кафедра фундаментальной и прикладной математики, теории и методики обучения математике.
Курсовая работа
«Ряды Фурье»
Выполнил: Студент 131 группы
Гаврутенко А.В.
Научный руководитель: профессор кафедры фундаментальной и прикладной математики,
теории и методики обучения математике
Менчер А.Э.
Чита 2009
Оглавление
Определение коэффициентов по методу Эйлера-Фурье
Ортогональные системы функций
Интеграл Дирихле Принцип локализаци
Представление функций рядом Фурье
Случай непериодической функции
Случай произвольного промежутка
Случай четных и нечетных функций
Примеры разложения функций в ряд Фурье
Список использованной литературы
Введение
В науке и технике часто приходиться иметь дело с периодическими явлениями, т. е. такими, которые воспроизводятся в прежнем виде через определенный промежуток времени Т, который называется периодом. Например, движение паровой машины повторяется, после того как пройдет полный цикл. Различные величины, связанные с периодическим явлением, по истечении периода Т возвращаются к своим прежним значениям и представляют собой периодические функции от времени t с периодом Т.
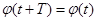
Если не считать постоянной, то простейшей периодической функцией является синусоидальная величина: 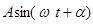 , где , где 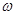 есть частота, связанная с периодом Т соотношением: есть частота, связанная с периодом Т соотношением:
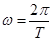 . .
Из подобных простейших периодических функций могут быть составлены и более сложные. Ясно, что составляющие синусоидальные величины должны быть разных частот, иначе их сложение не дает ничего нового, а вновь приводит к синусоидальной величине, причем той же частоты. Если же сложить величины вида:
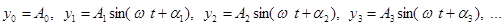 (1) (1)
которые имеют разные частоты
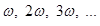 , ,
то получится периодическая функция, но уже существенно отличающаяся от величин, входящих в сумму.
Рассмотрим для примера сложение трех синусоидальных величин:
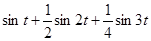

На рисунке мы видим, что график функции полученной в результате сложения трех синусоидальных величин (показан сплошной линией) уже значительно отличается от синусоиды. В большей степени это имеет место для суммы бесконечного ряда величин вида (1).
Теперь возникает обратный вопрос: можно ли данную периодическую функцию представить в виде суммы конечного или бесконечного множества синусоидальных величин вида (1).
Как будет показано ниже, на этот вопрос можно ответить удовлетворительно, но только лишь используя бесконечную последовательность величин вида (1). Для функций некоторого класса имеет место разложение в «тригонометрический ряд»:
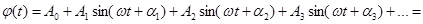 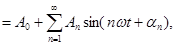 (2) (2)
С геометрической точки зрения это означает, что график периодической функции получается путем наложения ряда синусоид. Если же каждую синусоидальную величину истолковать механически как представляющую гармонические колебательные явления, то можно сказать, что здесь сложное колебание разлагается на отдельные гармонические колебания. Исходя из этого, отдельные синусоидальные величины, входящие в состав разложения (2), называют гармоническими составляющими функции 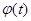 или просто ее первой, второй и т. д. гармониками. Сам же процесс разложения периодической функции на гармоники носит название гармонического анализа. или просто ее первой, второй и т. д. гармониками. Сам же процесс разложения периодической функции на гармоники носит название гармонического анализа.
Если за независимую переменную выбрать
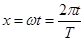 , ,
то получиться функция, зависящая от х, так же периодическая, но уже со стандартным периодом 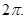 Разложение (2) в этом случаи примет вид: Разложение (2) в этом случаи примет вид:
 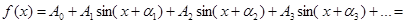
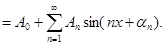 (3) (3)
Теперь развернув члены этого ряда по формуле синуса суммы и обозначив
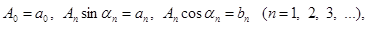
мы придем к окончательной форме тригонометрического разложения:
 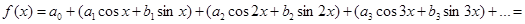
 (4) (4)
В данном разложении функция от угла х, имеющая период 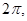 разложена по косинусам и синусам углов, кратных х. разложена по косинусам и синусам углов, кратных х.
Мы пришли к разложению функции в тригонометрический ряд, отправляясь от периодических, колебательных явлений и связанных с ними величин. Подобные разложения часто оказываются полезными и при исследовании функций, заданных в определенном конечном промежутке и вовсе не порожденных никакими колебательными явлениями.
В предыдущем параграфе было сказано, что существует ряд функций, которые можно представить в виде бесконечного тригонометрического ряда. Для того, что бы установить возможность разложения некоторой функции  , имеющей период , имеющей период 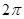 в тригонометрический ряд вида: в тригонометрический ряд вида:
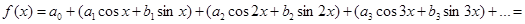
 (4) (4)
нужно иметь набор коэффициентов 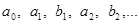
Прием для нахождения этих коэффициентов во второй половине XVIII века был применен Эйлером и независимо от него в начале XIX века—Фурье.
Впредь будем предполагать функцию  непрерывной или кусочнонепрерывной в промежутке непрерывной или кусочнонепрерывной в промежутке 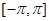 . .
Допустим, что разложение (4) имеет место. Проинтегрируем его почленно от 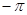 до до 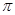 ; в результате получим: ; в результате получим:

Но, как легко видеть,
 (5) (5)
Поэтому все члены под знаком суммы будут равняться нулю, и окончательно получаем
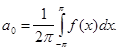 (6) (6)
Для того чтобы найти значение коэффициента  , умножим обе части равенства (4) на , умножим обе части равенства (4) на 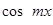 и снова проинтегрируем почленно в том же промежутке: и снова проинтегрируем почленно в том же промежутке:

В виду (5) 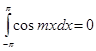 . .

если 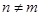 , и, наконец, , и, наконец,
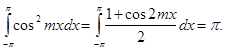 (9) (9)
Таким образом, обращаются в нуль все интегралы под знаком суммы, кроме интеграла, при котором множителем стоит именно коэффициент  . Отсюда получаем: . Отсюда получаем:
 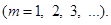
Аналогично, умножая разложение (4) на 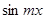 и затем, интегрируя почленно, определим коэффициент при синусе: и затем, интегрируя почленно, определим коэффициент при синусе:
 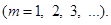
Формулы, по которым вычисляются коэффициенты 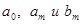 , называются формулами Эйлера-Фурье, а сами коэффициенты называются коэффициентами Фурье для данной функции. И, наконец, тригонометрический ряд (4), составленный по этим коэффициентам, получил название ряд Фурье для данной функции. , называются формулами Эйлера-Фурье, а сами коэффициенты называются коэффициентами Фурье для данной функции. И, наконец, тригонометрический ряд (4), составленный по этим коэффициентам, получил название ряд Фурье для данной функции.
Дадим теперь отчет в том, какова логическая ценность проведенных рассуждений. Мы исходили из того, что тригонометрический ряд (4) имеет место, поэтому вопрос о том, отвечает ли это действительности, остается открытым. Мы пользовались повторно почленным интегрированием ряда, а эта операция не всегда дозволительна, достаточным условием для применения операции является равномерная сходимость ряда. Поэтому строго установленным условием можно считать лишь следующее:
если функция f(x) разлагается в равномерно сходящийся тригонометрический ряд (4), то этот ряд будет являться ее рядом Фурье.
Если же не предполагать наперед равномерности сходимости, то все приведенные выше соображения не доказывают даже того, что функция может разлагаться только в ряд Фурье. Эти рассуждения можно рассматривать лишь как наведение, достаточное для того, чтобы в поисках тригонометрического разложения данной функции начать ее с ряда Фурье, обязуясь установить условия, при которых он сходится и притом именно к данной функции.
Пока этого не сделано, мы имеем право лишь формально рассматривать ряд Фурье данной функции, но не можем о нем ничего утверждать, кроме того, что он «порожден» функцией f(x). Эту связь обычно обозначают так:
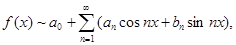
избегая знака равенства.
Две функции 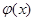 и и 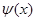 определенные на промежутке определенные на промежутке 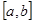 называются ортогональными на этом промежутке, если интеграл от их произведения равен нулю: называются ортогональными на этом промежутке, если интеграл от их произведения равен нулю:

Рассмотрим систему функций 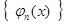 , определенных в промежутке [a, b] и непрерывных или кусочно-непрерывных. Если все функции данной системы попарно ортогональны, то есть , определенных в промежутке [a, b] и непрерывных или кусочно-непрерывных. Если все функции данной системы попарно ортогональны, то есть
 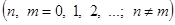
то ее называют ортогональной системой функций. При этом всегда будем полагать, что

Если 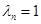 , то система называется нормальной. Если же это условие не выполняется, то можно перейти к системе , то система называется нормальной. Если же это условие не выполняется, то можно перейти к системе 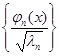 , которая уже заведомо будет нормальной. , которая уже заведомо будет нормальной.
Важнейшим примером ортогональной системы функций как раз и является тригонометрическая система
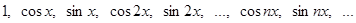 (10) (10)
в промежутке 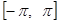 , которую мы рассматривали ранее. Ее ортогональность следует из соотношений (5), (7), (8). Однако она не будет нормальной ввиду (9). Умножая тригонометрические функции (10) на надлежащие множители, легко получить нормальную систему: , которую мы рассматривали ранее. Ее ортогональность следует из соотношений (5), (7), (8). Однако она не будет нормальной ввиду (9). Умножая тригонометрические функции (10) на надлежащие множители, легко получить нормальную систему:
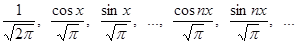 (10*) (10*)
Пусть в промежутке 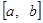 дана какая-нибудь ортогональная система функций дана какая-нибудь ортогональная система функций 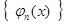 . Зададимся целью разложить определенную в . Зададимся целью разложить определенную в 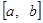 функцию функцию  в «ряд по функциям в «ряд по функциям 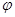 » вида: » вида:
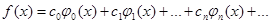 (11) (11)
Для определения коэффициентов данного разложения поступим так же, как мы это сделали в предыдущем параграфе, а именно умножим обе части равенства на 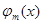 и проинтегрируем его почленно: и проинтегрируем его почленно:

В силу ортогональности системы, все интегралы справа, кроме одного, будут равны нулю, и легко получается:
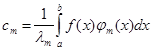 (m=0, 1, 2, …) (12) (m=0, 1, 2, …) (12)
Ряд (11) с коэффициентами, составленными по формулам (12), называется обобщенным рядом Фурье данной функции, а сами коэффициенты—ее обобщенными коэффициентами Фурье относительно системы 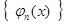 . В случаи нормальной системы функций коэффициенты будут определяться следующим образом: . В случаи нормальной системы функций коэффициенты будут определяться следующим образом:

В данном случаи все замечания сделанные в предыдущем параграфе необходимо повторить. Обобщенный ряд Фурье, построенный для функции  , связан с ней лишь формально и в общем случае эту связь обозначают следующим образом: , связан с ней лишь формально и в общем случае эту связь обозначают следующим образом:

Сходимость этого ряда, как и в случае тригонометрического ряда, подлежит еще исследованию.
Пусть 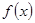 будет непрерывная или кусочно-непрерывная функция с периодом будет непрерывная или кусочно-непрерывная функция с периодом 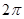 . Вычислим постоянные (ее коэффициенты Фурье): . Вычислим постоянные (ее коэффициенты Фурье):
 
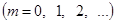 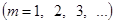
и по ним составим ряд Фурье нашей функции
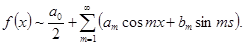
Как видим, здесь коэффициент 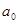 мы определили по общей формуле для мы определили по общей формуле для  при при 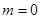 , но зато свободный член ряда запишем в виде , но зато свободный член ряда запишем в виде 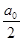 . .
Если функция F(x) кусочно-непрерывна в любом конечном промежутке и к тому же имеет период 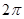 , то величина интеграла , то величина интеграла
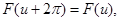
по прежнему промежутку длины 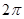 не зависит от не зависит от 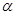 . .
Действительно, имеем

Если в последнем интеграла сделать подстановку 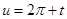 , то он приведется к интегралу , то он приведется к интегралу

и лишь знаком будет отличаться от первого интеграла. Таким образом, рассматриваемый интеграл оказывается равным интегралу

уже не содержащему 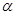 . .
Для того чтобы исследовать поведение ряда в какой-нибудь определенной точке 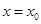 , составим удобное выражение для его частичной суммы , составим удобное выражение для его частичной суммы
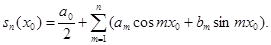
Подставим вместо  и и 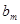 их интегральные выражения и подведем постоянные числа их интегральные выражения и подведем постоянные числа 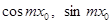 под знак интеграла: под знак интеграла:


Легко проверить тождество

Воспользуемся этим тождеством для преобразования подынтегрального выражения, окончательно получим
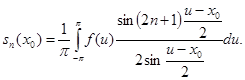 (13) (13)
Этот интеграл называют интегралом Дирихле, хотя у Фурье он встречается гораздо раньше.
Так как мы имеем дело с функцией от u периода 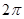 , то промежуток интегрирования , то промежуток интегрирования 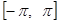 по сделанному выше замечанию можно заменить, например, промежутком по сделанному выше замечанию можно заменить, например, промежутком 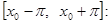

Подстановкой 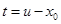 преобразуем этот интеграл к виду преобразуем этот интеграл к виду

Затем, разбивая интеграл на два: 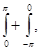 и приводя второй интеграл путем замены знака переменной тоже к промежутку и приводя второй интеграл путем замены знака переменной тоже к промежутку 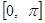 , придем к такому окончательному выражению для частичной суммы ряда Фурье: , придем к такому окончательному выражению для частичной суммы ряда Фурье:
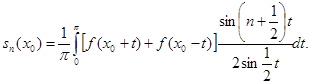 (14) (14)
Таким образом, дело сводится к исследованию поведения именно этого интеграла, содержащего параметр n.
Для дальнейшего изложения материала нам потребуется одна лемма, принадлежащая Риману, которую мы оставим без доказательства.
Если функция 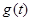 непрерывна или кусочно-непрерывна в некотором конечном промежутке непрерывна или кусочно-непрерывна в некотором конечном промежутке 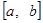 , то , то

и, аналогично,

Если вспомнить формулы, выражающие коэффициенты Фурье 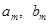 , то в качестве первого непосредственного следствия из леммы получается утверждение: , то в качестве первого непосредственного следствия из леммы получается утверждение:
Коэффициенты Фурье 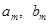 кусочно-непрерывной функции при кусочно-непрерывной функции при 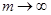 стремятся к нулю. стремятся к нулю.
Вторым непосредственным следствием является так называемый «принцип локализации».
Взяв произвольное положительное число 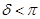 , разобьем интеграл в (14) на два: , разобьем интеграл в (14) на два:  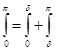 . Если второй из них переписать в виде . Если второй из них переписать в виде

то станет ясно, что множитель при синусе

является кусочно-непрерывной функцией от t в промежутке  . В этом случае по лемме этот интеграл при . В этом случае по лемме этот интеграл при 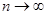 стремится к нулю, так что и само существование предела для частичной суммы ряда Фурье и величина этого предела целиком определяется поведением одного лишь интеграла стремится к нулю, так что и само существование предела для частичной суммы ряда Фурье и величина этого предела целиком определяется поведением одного лишь интеграла

Но в этот интеграл входят лишь значения функции f(x), отвечающие изменению аргумента в промежутке от  до до 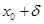 . Этим соображением доказывается «принцип локализации», состоящий в следующем: . Этим соображением доказывается «принцип локализации», состоящий в следующем:
Поведение ряда Фурье функции f(x) в некоторой точке 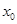 зависит исключительно от значений, принимаемых этой функцией в непосредственной близости рассматриваемой точки, т. е. в сколь угодно малой ее окрестности. зависит исключительно от значений, принимаемых этой функцией в непосредственной близости рассматриваемой точки, т. е. в сколь угодно малой ее окрестности.
Таким образом, если взять две функции, значения которых в произвольно малой окрестности 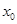 совпадают, то как бы они не расходились вне этой окрестности, соответствующие этим функциям ряды Фурье ведут себя в точке совпадают, то как бы они не расходились вне этой окрестности, соответствующие этим функциям ряды Фурье ведут себя в точке 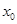 одинаково: либо оба сходятся, и притом к одной и той же сумме, либо оба расходятся. одинаково: либо оба сходятся, и притом к одной и той же сумме, либо оба расходятся.
Наложим на функцию f(x) более тяжелое требование, а именно—предположим ее кусочно-дифференцируемой в промежутке 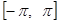 . .
Тогда имеет место общая теорема:
Теорема. Если функция f(x) с периодом 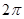 кусочно-дифференцируема в промежутке кусочно-дифференцируема в промежутке 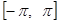 , то ее ряд Фурье в каждой точке , то ее ряд Фурье в каждой точке 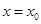 сходится и имеет сумму сходится и имеет сумму
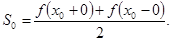
Эта сумма, очевидно, равна 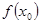 , если в точке , если в точке 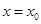 функция непрерывна. функция непрерывна.
Доказательство. Отметим, что равенство (14) имеет место для каждой функции f(x), удовлетворяющей поставленным условиям. Если, в частности, взять 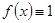 , то , то 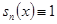 , и из (14) получим, что , и из (14) получим, что

Умножая обе части равенства на постоянное число 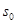 и вычитая результат из (14), найдем и вычитая результат из (14), найдем

для нашей цели нужно доказать, что интеграл справа при 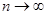 стремится к нулю. стремится к нулю.
Представим его в виде
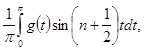 (15) (15)
где положено
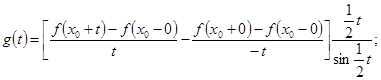 (16) (16)
если бы нам удалось установить что эта функция кусочно-непрерывна, то из леммы предыдущего параграфа следовало бы уже, что интеграл (15) имеет предел нулю при 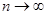 . Но в промежутке . Но в промежутке 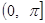 функция g(x) вообще непрерывна, за исключением разве лишь конечного числа точек, где она может иметь скачки—ибо такова функция f(x). Остается открытым лишь вопрос о поведении функции g(x) при функция g(x) вообще непрерывна, за исключением разве лишь конечного числа точек, где она может иметь скачки—ибо такова функция f(x). Остается открытым лишь вопрос о поведении функции g(x) при 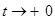 . .
Мы докажем существование конечного предела
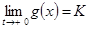 ; ;
положив тогда g(0)=K, мы в точке t=0 получим непрерывность, и применение леммы окажется оправданным. Но второй множитель в правой части равенства (16) явно имеет пределом единицу; обратимся к выражению квадратных скобках.
Пусть, для простаты, сначала точка 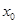 лежит внутри промежутка, где функция f(x) дифференцируема. Тогда лежит внутри промежутка, где функция f(x) дифференцируема. Тогда 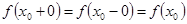 , и каждое из соотношений , и каждое из соотношений
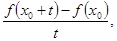 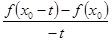 (17) (17)
стремится к пределу 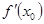 , а , а  — к нулю. Если же — к нулю. Если же 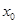 есть «точка стыка», то при этом она может оказаться как точкой непрерывности, так и точкой разрыва. В первом случае мы опять столкнемся с отношением (17), но они будут стремиться на этот раз к различным пределам, соответственно—к производной справа и к производной слева. К аналогичному результату придем и в случае разрыва, но здесь есть «точка стыка», то при этом она может оказаться как точкой непрерывности, так и точкой разрыва. В первом случае мы опять столкнемся с отношением (17), но они будут стремиться на этот раз к различным пределам, соответственно—к производной справа и к производной слева. К аналогичному результату придем и в случае разрыва, но здесь 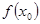 заменится значениями заменится значениями 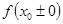 тех функций, от склеивания которых получилась данная, а пределами отношений (17) будут односторонние производные упомянутых функций при тех функций, от склеивания которых получилась данная, а пределами отношений (17) будут односторонние производные упомянутых функций при 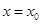 . .
Итак, наше заключение справедливо во всех случаях.
Вся построенная выше теория исходила из предположения, что заданная функция определена для всех вещественных значений x и притом имеет период 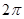 . Между тем чаще всего приходится иметь дело с непериодической функцией f(x), иной раз даже заданной только в промежутке . Между тем чаще всего приходится иметь дело с непериодической функцией f(x), иной раз даже заданной только в промежутке 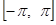 . .
Что бы иметь право применить к такой функции изложенную теорию, введем взамен нее вспомогательную функцию 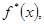 определенную следующим образом. В промежутке определенную следующим образом. В промежутке 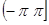 мы отождествляем мы отождествляем 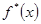 с f(x): с f(x):
 (18) (18)
затем полагаем
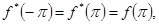
а на остальные вещественные значения x распространяем функцию 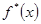 по закону периодичности. по закону периодичности.
К построенной таким образом функции 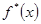 с периодом с периодом 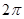 можно уже применить доказанную теорему разложения. Однако, если речь идет о точке можно уже применить доказанную теорему разложения. Однако, если речь идет о точке 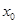 , строго лежащей между , строго лежащей между 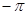 и и 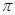 , то, ввиду (18), нам пришлось бы иметь дело с заданной функцией , то, ввиду (18), нам пришлось бы иметь дело с заданной функцией 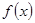 . По той же причине и коэффициенты разложения можно вычислить по формулам вычисления коэффициентов не переходя к вспомогательной функции. Короче говоря, все доказанное выше непосредственно переносится на заданную функцию . По той же причине и коэффициенты разложения можно вычислить по формулам вычисления коэффициентов не переходя к вспомогательной функции. Короче говоря, все доказанное выше непосредственно переносится на заданную функцию 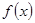 , минуя вспомогательную функцию , минуя вспомогательную функцию 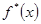 . .
Особого внимания, однако, требуют концы промежутка 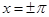 . При применении к функции . При применении к функции 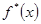 теоремы предыдущего параграфа, скажем, в точке теоремы предыдущего параграфа, скажем, в точке 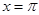 , нам пришлось бы иметь дело как со значениями вспомогательной функции , нам пришлось бы иметь дело как со значениями вспомогательной функции 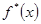 справа от справа от 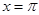 , где они совпадают уже со значениями , где они совпадают уже со значениями 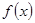 справа от справа от 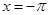 ю Поэтому для ю Поэтому для 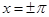 в качестве значения в качестве значения 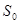 надлежало бы взять надлежало бы взять
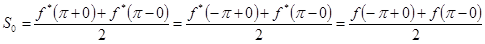 . .
Таким образом, если заданная функция 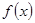 даже непрерывна при даже непрерывна при 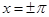 , но не имеет периода , но не имеет периода 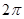 , так что , так что 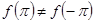 , то—при соблюдении требований кусочной дифференцируемости—суммой ряда Фурье будет число , то—при соблюдении требований кусочной дифференцируемости—суммой ряда Фурье будет число
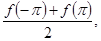
отличное как от 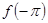 , так и от , так и от  . Для такой функции разложение имеет место лишь в открытом промежутке . Для такой функции разложение имеет место лишь в открытом промежутке  . .
Следующее замечание так же заслуживает особого внимания. Если тригонометрический ряд
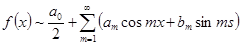
сходится в промежутке 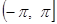 к функции к функции 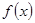 , то ввиду того, что его члены имеют период , то ввиду того, что его члены имеют период 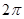 , он сходится всюду, и сумма его , он сходится всюду, и сумма его 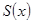 тоже оказывается периодической функцией с периодом тоже оказывается периодической функцией с периодом 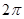 . Но эта сумма вне указанного промежутка вообще уже не совпадает с функцией . Но эта сумма вне указанного промежутка вообще уже не совпадает с функцией 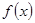 . .
Предположим, что функция 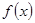 задана в промежутке задана в промежутке 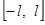 произвольной длины произвольной длины 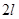 и кусочно-дифференцируема в нем. Если прибегнуть к подстановке и кусочно-дифференцируема в нем. Если прибегнуть к подстановке
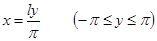 , ,
то получится функция 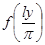 от от 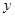 в промежутке в промежутке 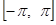 , тоже кусочно-дифференцируемая, к которой уже приложим рассмотрения предыдущего параграфа. Как мы видели, за исключением точек разрыва и концов промежутка, можно разложить ее в ряд Фурье: , тоже кусочно-дифференцируемая, к которой уже приложим рассмотрения предыдущего параграфа. Как мы видели, за исключением точек разрыва и концов промежутка, можно разложить ее в ряд Фурье:

коэффициенты которого определяются формулами Эйлера—Фурье:
 
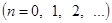 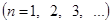
вернемся теперь к прежней переменной 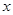 , полагая , полагая
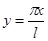 . .
Тогда получим разложение заданной функции 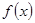 в тригонометрический ряд несколько измененного вида: в тригонометрический ряд несколько измененного вида:
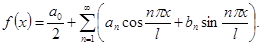 (19) (19)
Здесь косинусы и синусы берутся от углов, кратных не 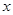 , а , а 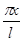 . Можно было бы и формулы для определения коэффициентов разложения преобразовать той же подстановкой к виду . Можно было бы и формулы для определения коэффициентов разложения преобразовать той же подстановкой к виду
 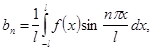 (20) (20)
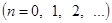 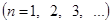
В отношении концов промежутка 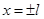 сохраняют силу замечания, сделанные в предыдущем параграфе относительно точек сохраняют силу замечания, сделанные в предыдущем параграфе относительно точек 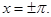 Конечно, промежуток Конечно, промежуток 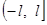 может быть заменен любым другим промежутком длинны может быть заменен любым другим промежутком длинны 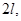 в частности, промежутком в частности, промежутком 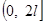 . В последнем случае формулы (20) должны быть заменены формулами . В последнем случае формулы (20) должны быть заменены формулами
 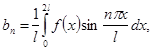 (20a) (20a)
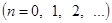 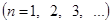
Если заданная в промежутке 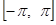 функция функция 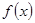 будет нечетной, то очевидно будет нечетной, то очевидно

В этом легко убедится:
 . .
Таким же путем устанавливается, что в случае четной функции 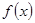 : :
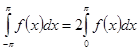 . .
Пусть теперь 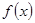 будет кусочно-дифференцируемая в промежутке будет кусочно-дифференцируемая в промежутке 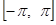 четная функция. Тогда произведение четная функция. Тогда произведение 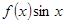 окажется нечетной функцией, и по сказанному окажется нечетной функцией, и по сказанному

Таким образом, ряд Фурье четной функции содержит одни лишь косинусы:
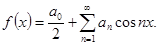 (21) (21)
Так как  в этом случае будет тоже четной функцией, то, применив сюда второе из сделанных выше замечаний, можем коэффициенты в этом случае будет тоже четной функцией, то, применив сюда второе из сделанных выше замечаний, можем коэффициенты 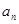 разложения написать в виде разложения написать в виде
 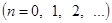 (22) (22)
Если же функция 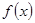 будет нечетной, то нечетной будет и функция будет нечетной, то нечетной будет и функция  , так что , так что
 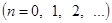
Мы приходим к заключению, что ряд Фурье нечетной функции содержит одни лишь синусы:
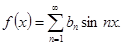 (23) (23)
При этом ввиду четности произведения  можно писать: можно писать:
 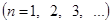 (24) (24)
Отметим, что каждая функция 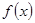 , заданная в промежутке , заданная в промежутке 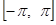 , может быть представлена в виде суммы четной и нечетной составляющих функций: , может быть представлена в виде суммы четной и нечетной составляющих функций:
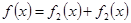 , ,
Где
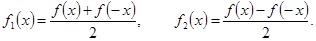
Очевидно, что ряд Фурье функции 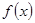 как раз и составится из разложения по косинусам функции как раз и составится из разложения по косинусам функции 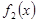 и разложения по синусам функции и разложения по синусам функции 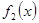 . .
Предположим, далее, что функция 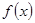 задана лишь в промежутке задана лишь в промежутке 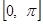 . Желая разложить ее в этом промежутке в ряд Фурье мы дополним определение нашей функции для значений x в промежутке . Желая разложить ее в этом промежутке в ряд Фурье мы дополним определение нашей функции для значений x в промежутке 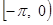 по произволу, но с сохранением кусочной дифференцируемости, а затем применим сказанное в пункте «Случай непериодической функции». по произволу, но с сохранением кусочной дифференцируемости, а затем применим сказанное в пункте «Случай непериодической функции».
Можно использовать произвол в определении функции в промежутке 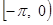 так, что бы получить для так, что бы получить для 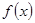 разложение только лишь по косинусам или только по синусам. Действительно, представим семе, что для разложение только лишь по косинусам или только по синусам. Действительно, представим семе, что для 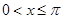 мы полагаем мы полагаем 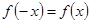 , так что в результате получается четная функция в промежутке , так что в результате получается четная функция в промежутке 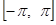 . Ее разложение, как мы видели, будет содержать одни лишь косинусы. Коэффициенты разложения можно вычислять по формулам (22), куда входят лишь значения первоначально заданной функции . Ее разложение, как мы видели, будет содержать одни лишь косинусы. Коэффициенты разложения можно вычислять по формулам (22), куда входят лишь значения первоначально заданной функции 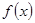 . .
Аналогично, если дополнить определение функции 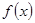 по закону нечетности, то она станет нечетной и в ее разложении будут одни лишь синусы. Коэффициенты ее разложения определяются по формулам (24). по закону нечетности, то она станет нечетной и в ее разложении будут одни лишь синусы. Коэффициенты ее разложения определяются по формулам (24).
Таким образом, заданную в промежутке 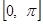 функцию при соблюдении условий оказывается возможным разлагать как по косинусам, так и по одним лишь синусам. функцию при соблюдении условий оказывается возможным разлагать как по косинусам, так и по одним лишь синусам.
Особого исследования требуют точки 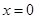 и и 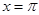 . Здесь оба разложения ведут себя по-разному. Предположим, для простоты, что заданная функция . Здесь оба разложения ведут себя по-разному. Предположим, для простоты, что заданная функция 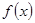 непрерывна при непрерывна при 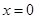 и и 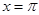 , и рассмотрим сначала разложение по косинусам. Условие , и рассмотрим сначала разложение по косинусам. Условие 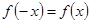 , прежде всего, сохраняет непрерывность при , прежде всего, сохраняет непрерывность при 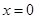 , так что ряд (21) при , так что ряд (21) при 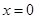 будет сходиться именно к будет сходиться именно к 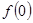 . Так как, далее, . Так как, далее,
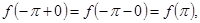
то и при 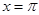 имеет месть аналогичное обстоятельство. имеет месть аналогичное обстоятельство.
Иначе обстоит дело с разложением по синусам. В точках 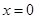 и и 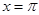 сумма ряда (23) явно будет нулем. Поэтому она может дать нам значения сумма ряда (23) явно будет нулем. Поэтому она может дать нам значения 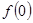 и и 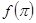 , очевидно, лишь в том случае, если эти значения равны нулю. , очевидно, лишь в том случае, если эти значения равны нулю.
Если функция 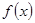 задана в промежутке задана в промежутке 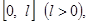 то, прибегнув к той же замене переменной, что и в предыдущем параграфе, мы сведем вопрос о разложении ее в ряд по косинусам то, прибегнув к той же замене переменной, что и в предыдущем параграфе, мы сведем вопрос о разложении ее в ряд по косинусам
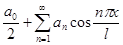
или в ряд по синусам
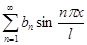
к только что рассмотренному. При этом коэффициенты разложений вычисляются, соответственно, по формулам
 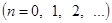
или
 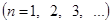 . .
Функции, которые ниже приводятся в качестве примеров, как правило, относятся к классу дифференцируемых или кусочно-дифференцируемых. Поэтому сама возможность их разложения в ряд Фурье—вне сомнения, и на этом мы останавливаться не будем.
Все задания взяты из Сборника задач и упражнений по математическому анализу, Б. Н. Демидович.
№ 2636. Функцию 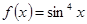 разложить в ряд Фурье. разложить в ряд Фурье.
Так как функция  является нечетной, то, следовательно, является нечетной, то, следовательно, 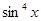 будет четной. Поэтому ее разложение в ряд Фурье содержит одни лишь косинусы. будет четной. Поэтому ее разложение в ряд Фурье содержит одни лишь косинусы.
Найдем коэффициенты разложения;


№ 2938. Разложить в ряд Фурье функцию 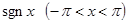 . Изобразить этой функции и графики нескольких частных сумм ряда Фурье этой функции. . Изобразить этой функции и графики нескольких частных сумм ряда Фурье этой функции.

Функция 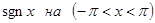 нечетная, поэтому ее разложение будет содержать одни лишь синусы. нечетная, поэтому ее разложение будет содержать одни лишь синусы.

То есть, получается, что при четных значениях n коэффициент 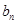 , а следовательно и все слагаемое, обращается в нуль. Поэтому суммирование идет только лишь по четным значениям n. , а следовательно и все слагаемое, обращается в нуль. Поэтому суммирование идет только лишь по четным значениям n.
Ряд Фурье для этой функции примет следующий вид:
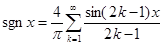 . . 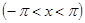
Ниже изображены графики функций 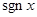 и нескольких частных сумм ряда Фурье: и нескольких частных сумм ряда Фурье:
График функции 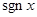 , , 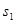 , , 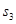 и и 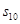

№ 2940. 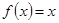 в интервале в интервале 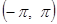 . .
Функция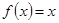 нечетная. нечетная.

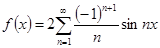
№ 2941. 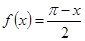 в интервале в интервале 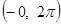 . .



В итоге получаем ряд Фурье:
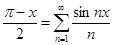 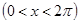
№ 2941. 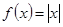 в интервале в интервале 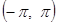 . .
Функция 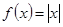 четная. четная.


Как и в № 2938, у нас при четных значениях n коэффициент 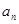 обращается в нуль. Поэтому суммировать будем лишь по нечетным значениям. обращается в нуль. Поэтому суммировать будем лишь по нечетным значениям.
В итоге получим:
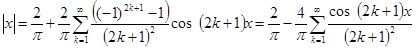
№ 2950. 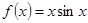 в интервале в интервале 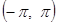 . .
Функция 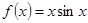 четная. четная.


Так как при n=1 знаменатель обращается в нуль, то суммирование необходимо произвести начиная в двойки.
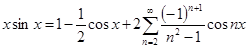
№ 2951. 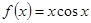 в интервале в интервале  . .
Функция 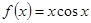 нечетная. нечетная.


№ 2961. Функцию 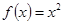 разложить а) в интервале разложить а) в интервале 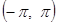 по косинусам кратных дуг; б) в интервале по косинусам кратных дуг; б) в интервале 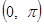 по синусам кратных дуг; в) в интервале по синусам кратных дуг; в) в интервале  . Изобразить график функции . Изобразить график функции 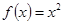 и сумм рядов Фурье для каждого отдельного случая. Используя разложения, найти суммы рядов: и сумм рядов Фурье для каждого отдельного случая. Используя разложения, найти суммы рядов: 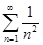 ; ; 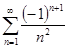 и и 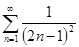 . .
а) 

И, наконец получаем разложение в ряд Фурье:
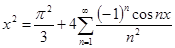 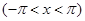

б) 
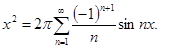 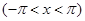

в) 


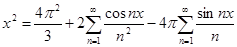 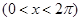

№ 2962 Исходя из разложения
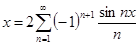 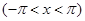 , ,
почленным интегрированием получить разложение в ряд Фурье на интервале 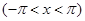 функций функций 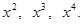
Проинтегрируем равенство 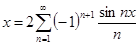 почленно, получим почленно, получим
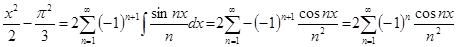
И окончательно получаем:
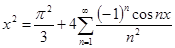 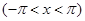
Проинтегрируем полученное равенство повторно
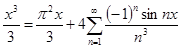
или отсюда получаем
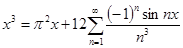 . .
1 И.М. Уваренков, М.З. Маллер „Курс математического анализа”, М., „Просвещение”, 1976 г.
2 Г.М. Фихтенгольц „Курс дифференциального и интегрального исчисления”, том III, издание 8, М., „ФИЗМАТЛИТ”, 2005г.
3 В.Е. Шнейдер, А.И. Слуцкий, А.С. Шумов „Краткий курс высшей математики”, том2, М., „Высшая школа”, 1978г.
4 Н.Я. Виленкин, В.В. Цукерман, М.А. Доброхотова, А.Н. Сафонов „Ряды”, М. „Просвещение”, 1982г.
5 Б.П. Демидович „Сборник задач и упражнений по математическому анализу” издание 9, М. „Наука”, 1977г.
|