|
Большинство численных методов решения задач математического анализа так или иначе связано с аппроксимацией функций. Это и собственно задачи приближения функций (интерполяция, сглаживание, наилучшие приближения) и задачи, в которых аппроксимация присутствует как промежуточный этап исследования (численное дифференцирование и интегрирование, численное решение дифференциальных и интегральных уравнений).
Типичной задачей приближения является задача интерполяции: по заданной таблице чисел 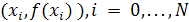 , восстановить функцию , восстановить функцию 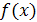 с той или иной точностью на отрезке [а, b] действительной оси. Классический метод ее решения состоит в построении интерполяционного многочлена Лагранжа, определяемого равенством с той или иной точностью на отрезке [а, b] действительной оси. Классический метод ее решения состоит в построении интерполяционного многочлена Лагранжа, определяемого равенством
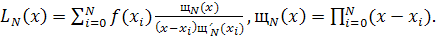

Хотя согласно теореме Вейерштрасса всякая непрерывная функция 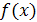 на отрезке на отрезке 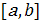 может быть как угодно хорошо приближена многочленами, практические возможности применения многочленов Лагранжа ограничены. Прежде всего, используя подобный аппарат, мы должны быть уверены, что, выбрав достаточно большое число узлов интерполяции, получим хорошее приближение интерполируемой функции. Однако, как показывает ряд простых примеров, это часто нельзя гарантировать. может быть как угодно хорошо приближена многочленами, практические возможности применения многочленов Лагранжа ограничены. Прежде всего, используя подобный аппарат, мы должны быть уверены, что, выбрав достаточно большое число узлов интерполяции, получим хорошее приближение интерполируемой функции. Однако, как показывает ряд простых примеров, это часто нельзя гарантировать.
С. Н. Бернштейном (1916 г.) было установлено, что последовательность интерполяционных многочленов Лагранжа построенных для непрерывной функции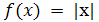 на отрезке [—1, 1] по равноотстоящим узлам на отрезке [—1, 1] по равноотстоящим узлам 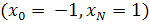 , с возрастанием , с возрастанием 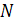 не стремится к не стремится к 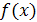 . Еще более любопытен другой пример, восходящий к Рунге (1901 г.) и состоящий в том, что указанный интерполяционный процесс не сходится на [—1, 1] даже для гладкой сколь угодно раз дифференцируемой функции . Еще более любопытен другой пример, восходящий к Рунге (1901 г.) и состоящий в том, что указанный интерполяционный процесс не сходится на [—1, 1] даже для гладкой сколь угодно раз дифференцируемой функции 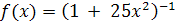 (рис. 0.1). В обоих случаях (рис. 0.1). В обоих случаях
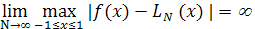
Иногда эти трудности удается преодолеть путем специального выбора узлов интерполяции или за счет перехода к каким-либо обобщенным многочленам. Однако такой путь, как правило, весьма усложняет вычисления и к тому же не избавляет нас от второй проблемы — быстрого накопления ошибок округления с ростом степени многочлена. Поэтому на практике для того, чтобы достаточно хорошо приблизить функцию, вместо построения интерполяционного многочлена высокой степени используют интерполяцию кусочными многочленами.
Примером такого рода является кусочно-линейная интерполяция. В общем случае отрезок 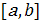 точками точками 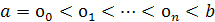 разбивается на части и на каждом промежутке разбивается на части и на каждом промежутке 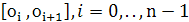 , строится свой интерполяционный многочлен. Полученные таким образом многочлены (обычно одной и той же степени) дают интерполяцию функции , строится свой интерполяционный многочлен. Полученные таким образом многочлены (обычно одной и той же степени) дают интерполяцию функции 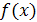 на всем отрезке на всем отрезке 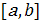 , которая, вообще говоря, не обеспечивает гладкого перехода от одного звена к другому и может быть даже разрывной, если точки , которая, вообще говоря, не обеспечивает гладкого перехода от одного звена к другому и может быть даже разрывной, если точки 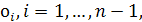 не включаются в число узлов интерполяции. Это допустимо, если не требуется восстанавливать функцию с заданной степенью гладкости. В частности, различные таблицы составляются с таким шагом, чтобы промежуточные значения функции с принятой точностью можно было вычислить с помощью линейной или квадратичной интерполяции. Для гладкого восстановления таблично заданной функции нужно увеличить степень составляющих многочленов, а остающиеся свободными коэффициенты определять из условий гладкого сопряжения многочленов на соседних промежутках. Получающиеся при этом гладкие кусочно-многочленные функции с однородной структурой (составленные из многочленов одной и той же степени) называются сплайн-функциями или просто сплайнами. Простейший и исторически самый старый пример сплайна - ломаная. не включаются в число узлов интерполяции. Это допустимо, если не требуется восстанавливать функцию с заданной степенью гладкости. В частности, различные таблицы составляются с таким шагом, чтобы промежуточные значения функции с принятой точностью можно было вычислить с помощью линейной или квадратичной интерполяции. Для гладкого восстановления таблично заданной функции нужно увеличить степень составляющих многочленов, а остающиеся свободными коэффициенты определять из условий гладкого сопряжения многочленов на соседних промежутках. Получающиеся при этом гладкие кусочно-многочленные функции с однородной структурой (составленные из многочленов одной и той же степени) называются сплайн-функциями или просто сплайнами. Простейший и исторически самый старый пример сплайна - ломаная.
Термин сплайн произошел от английского spline, что в переводе означает рейка, стержень — название приспособления, которое применяли чертежники для проведения гладких кривых через заданные точки. Возьмем гибкую стальную линейку, поставим ее на ребро и, закрепив один конец в заданной точке 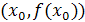 , поместим между опорами, которые располагаются так, чтобы линейка проходила через заданные точки (рис, 0.2). , поместим между опорами, которые располагаются так, чтобы линейка проходила через заданные точки (рис, 0.2).

Согласно закону Бернулли—Эйлера линеаризованное дифференциальное уравнение изогнутой оси линейки имеет вид
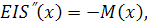
где 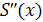 — вторая производная прогиба, — вторая производная прогиба,  — изгибающий момент, изменяющийся линейно от одной точки опоры к другой, — изгибающий момент, изменяющийся линейно от одной точки опоры к другой, 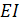 — жесткость. Проинтегрировав это уравнение, получим, что функция — жесткость. Проинтегрировав это уравнение, получим, что функция 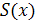 , описывающая профиль линейки, является кубическим многочленом между двумя соседними точками опоры и дважды непрерывно дифференцируемой функцией на всем промежутке интегрирования. Для определенности задачи на концах должны быть заданы краевые условия, в частности, при отсутствии внешних нагрузок па линейку , описывающая профиль линейки, является кубическим многочленом между двумя соседними точками опоры и дважды непрерывно дифференцируемой функцией на всем промежутке интегрирования. Для определенности задачи на концах должны быть заданы краевые условия, в частности, при отсутствии внешних нагрузок па линейку 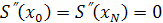 . .
Функция 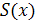 представляет собой другой пример (теперь уже гладкого) сплайна. Она относится к интерполяционным кубическим сплайнам, обладающим рядом замечательных свойств, которые и обеспечили им успех в приложениях. представляет собой другой пример (теперь уже гладкого) сплайна. Она относится к интерполяционным кубическим сплайнам, обладающим рядом замечательных свойств, которые и обеспечили им успех в приложениях.
В отличие от интерполяционных многочленов Лагранжа, последовательность интерполяционных кубических сплайнов на равномерной сетке узлов всегда сходится к интерполируемой непрерывной функции, причем сходимость повышается с улучшением дифференциальных свойств функции 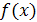 . Так, для функции . Так, для функции 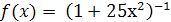 из примера Рунге кубический сплайн на сетке с числом узлов из примера Рунге кубический сплайн на сетке с числом узлов 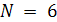 дает погрешность того же порядка, что и многочлен дает погрешность того же порядка, что и многочлен 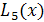 , но для , но для 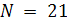 она настолько мала, что в масштабах рис. 0.1 не может быть показана (ср. с многочленом она настолько мала, что в масштабах рис. 0.1 не может быть показана (ср. с многочленом  ). ).
Алгоритмы построения кубических сплайнов являются весьма простыми и эффективно реализуются на ЭВМ, причем влияние ошибок округления при вычислениях оказывается незначительным.
Целью данной работы является изучение сплайнов, в частности базисных сплайнов. Также мы составим программу для работы со сплайнами.
§1. Определение сплайнов. Пространство сплайнов
Пусть на отрезке [a, b] задано разбиение 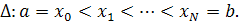 Для целого Для целого 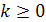 через через 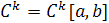 обозначим множество обозначим множество 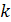 раз непрерывно дифференцируемых на раз непрерывно дифференцируемых на 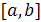 функций, а через функций, а через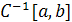 — множество кусочно-непрерывных функций с точками разрыва первого рода. — множество кусочно-непрерывных функций с точками разрыва первого рода.
Определение. Функция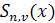 называется сплайном степени называется сплайном степени 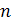 дефекта дефекта 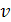 ( (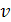 — целое число, — целое число, 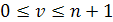 ) с узлами на сетке ) с узлами на сетке 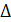 , если , если
а) на каждом отрезке  функция функция 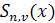 является многочленом степени является многочленом степени 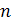 , т. е. , т. е.
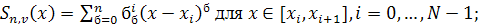 (1) (1)
б) 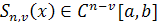 . .
Определение сплайна имеет смысл на всей вещественной оси ,если положить 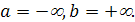
При этом на полуоси 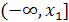 берется только формула (2), а на полуоси берется только формула (2), а на полуоси 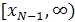 только формула (1). только формула (1).
Итак, сплайн 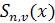 имеет непрерывные производные до порядка имеет непрерывные производные до порядка 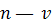 . Производные сплайна порядка выше . Производные сплайна порядка выше 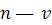 , вообще говоря, терпят разрывы в точках , вообще говоря, терпят разрывы в точках 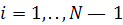 . Для определенности будем считать, что функция . Для определенности будем считать, что функция 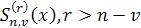 , непрерывна справа, т. е. , непрерывна справа, т. е.
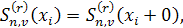
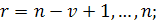
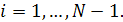
Множество сплайнов, удовлетворяющих определению, обозначим через 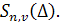 Ясно, что этому множеству принадлежат и сплайны степени n дефекта Ясно, что этому множеству принадлежат и сплайны степени n дефекта 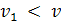 и сплайны степени и сплайны степени 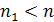 дефекта дефекта 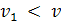 , если , если 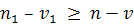 , в том числе многочлены степени не выше , в том числе многочлены степени не выше 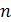 . Так как обычные операции сложения элементов из . Так как обычные операции сложения элементов из 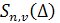 и их умножения на действительные числа не выводят за пределы множества, то оно является линейным множеством или линейным пространством. и их умножения на действительные числа не выводят за пределы множества, то оно является линейным множеством или линейным пространством.
Простейшим примером сплайна является единичная функция Хевисайда
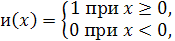
с которой естественным образом связана усеченная степенная функция
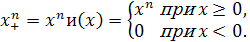
Функции 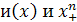 являются сплайнами соответственно нулевой степени и степени являются сплайнами соответственно нулевой степени и степени 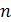 дефекта 1 с единственным узлом в нулевой точке (рис. 1.1). Мы будем рассматривать также усеченные степенные функции дефекта 1 с единственным узлом в нулевой точке (рис. 1.1). Мы будем рассматривать также усеченные степенные функции 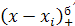 , связанные с точками сетки , связанные с точками сетки 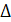 . При . При 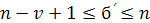 они принадлежат множеству они принадлежат множеству 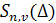
Теорема 1.1. Функции
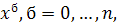
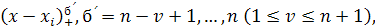 (3) (3)
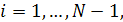
линейно независимы и образуют базис в пространстве 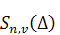 размерности размерности 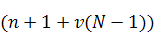
Доказательство: Предположим противное, т. е. что существуют постоянные 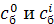 , не все равные нулю и такие, что , не все равные нулю и такие, что 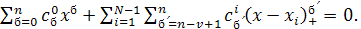
Тогда для 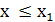 имеем имеем 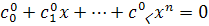 и в силу линейной независимости функций и в силу линейной независимости функций 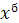 находим находим 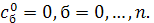 Беря Беря  получаем получаем  и, по той же причине, и, по той же причине, 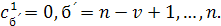 Продолжая этот процесс, убеждаемся, что все Продолжая этот процесс, убеждаемся, что все 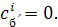 Следовательно, функции (3) линейно независимы. Следовательно, функции (3) линейно независимы.
Пусть теперь задан сплайн 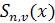 на отрезке на отрезке 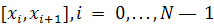 он является многочленом степени он является многочленом степени 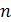 , , 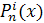 и может быть записан в виде (1) или (2). При этом, так как первые и может быть записан в виде (1) или (2). При этом, так как первые 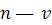 производных сплайна непрерывны в точках производных сплайна непрерывны в точках 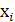 т. е. т. е.
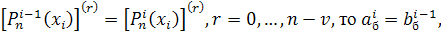
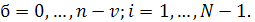
Покажем, что сплайн 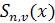 , на отрезке , на отрезке 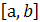 может быть представлен в виде может быть представлен в виде
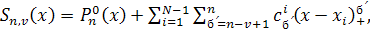 (4) (4)
Где 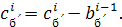
Действительно, преобразуя это выражение при 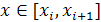 получаем получаем
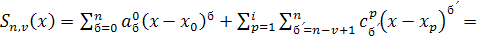
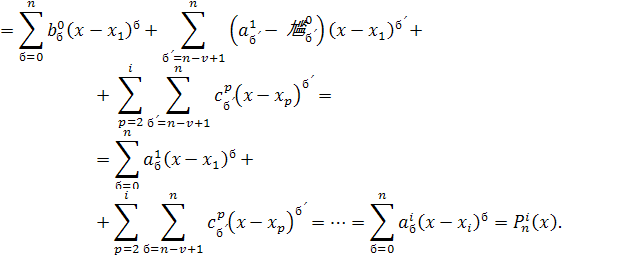
Это доказывает, что всякий сплайн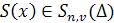 может быть представлен в виде линейной комбинации функций (3), т. е. эти функции образуют базис в может быть представлен в виде линейной комбинации функций (3), т. е. эти функции образуют базис в 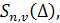 и представление (4) единственно. Эта формула называется представлением сплайна в виде суммы усеченных степенных функций. Итак, множество и представление (4) единственно. Эта формула называется представлением сплайна в виде суммы усеченных степенных функций. Итак, множество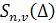 является конечномерным пространством размерности является конечномерным пространством размерности 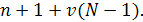
§2. Базисные сплайны с конечными носителями
В математическом анализе встречаются конструкции, связанные с финитными функциями, т. е. гладкими функциями, которые определяются на всей действительной оси, но отличны от нуля лишь на некотором конечном интервале (носителе). Ниже мы исследуем финитные сплайны из пространства 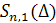 . В последующем изложении они играют исключительно важную роль. . В последующем изложении они играют исключительно важную роль.
Расширим сетку 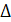 , добавив дополнительно точки , добавив дополнительно точки 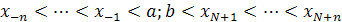 (можно положить, например, (можно положить, например, 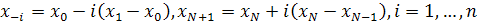 ). ).
Возьмем функцию и построим для нее разделенные разности и построим для нее разделенные разности  порядка по значениям аргумента порядка по значениям аргумента  . В результате получаются функции переменной х: . В результате получаются функции переменной х:

Так как для разделенной разности  порядка от функции порядка от функции  по точкам по точкам справедливо равенство справедливо равенство

Если использовать тождество  то можно получить несколько иную форму записи этой функции то можно получить несколько иную форму записи этой функции

Из определения усеченных степенных функций следует, что функция является сплайном степени п дефекта 1 на является сплайном степени п дефекта 1 на
сетке узлов
Лемма 1.1. Справедливо тождество

Доказательство. Если то разделенная разность функции то разделенная разность функции  по точкам по точкам  может быть вычислена по формуле Лейбница: может быть вычислена по формуле Лейбница:

Для разности  порядка путем рассуждений по индукции нетрудно получить порядка путем рассуждений по индукции нетрудно получить

Представим функцию в виде в виде
 
и построим ее разделенную разность  порядка по формуле Лейбница. Получим порядка по формуле Лейбница. Получим

Отсюда, если учесть определение сплайнов , следует тождество (4). , следует тождество (4).
Лемма 1.2. Сплайны  обладают следующими свойствами: обладают следующими свойствами:

Доказательство. Функция равна нулю при равна нулю при  и является многочленом степени n от х при и является многочленом степени n от х при  . Поэтому ее разделенные разности . Поэтому ее разделенные разности  порядка по значениям аргумента порядка по значениям аргумента тождественно равны нулю при тождественно равны нулю при  и и  т.е. т.е.  Внутри интервала Внутри интервала
В самом деле, при n = 0 согласно (2)  . Пусть, далее, утверждение а) верно при . Пусть, далее, утверждение а) верно при  Тогда при n
=
l
в силу (4) на интервале Тогда при n
=
l
в силу (4) на интервале функция функция является линейной комбинацией с положительными весами функций является линейной комбинацией с положительными весами функций причем по предположению в произвольной точке указанного интервала хотя бы одна из этих функций больше нуля. Следовательно, причем по предположению в произвольной точке указанного интервала хотя бы одна из этих функций больше нуля. Следовательно, для для  , и утверждение а) установлено. , и утверждение а) установлено.
Докажем утверждение б). Всякую n+1 раз непрерывно дифференцируемую функцию g(t) на промежутке а ≤ t ≤ b можно представить формулой Тейлора с остаточным членом в интегральной форме:

Здесь под знаком интеграла вместо обычного сомножителя стоит усеченная степенная функция, что позволяет заменить переменный верхний предел t постоянной величиной b. Из (7) следует разностное соотношение стоит усеченная степенная функция, что позволяет заменить переменный верхний предел t постоянной величиной b. Из (7) следует разностное соотношение

то, полагая g(x) =
xn
+1
, поручаем

Поскольку вне интервала (а, b), то это равенство -совпадает с (6) и лемма доказана.
Лемма 1.3. Функции являются сплайнами степени п дефекта 1 с конечными носителями минимальной длины. являются сплайнами степени п дефекта 1 с конечными носителями минимальной длины.
Доказательство. Предположим, что существует сплайн  отличный от нуля на интервале, меньшем, чем отличный от нуля на интервале, меньшем, чем  Такой интервал, очевидно, не может иметь границей точку, не являющуюся узлом сетки Такой интервал, очевидно, не может иметь границей точку, не являющуюся узлом сетки  . Поэтому пусть это будет интервал (xi
, xi
+
n
). . Поэтому пусть это будет интервал (xi
, xi
+
n
).
Возьмем представление сплайна дефекта v = 1 через усеченные степенные функции (1.4). Вследствие того, что  при при  в этом представлении в этом представлении  . Так как . Так как  при при  то ее производные до порядка n — 1 равны нулю в точке xi
+
n
. Имеем то ее производные до порядка n — 1 равны нулю в точке xi
+
n
. Имеем

Последние равенства представляют собой однородную систему линейных уравнений для определения коэффициентов   . Ее определитель пропорционален определителю Вандермонда n-ro порядка, который отличен от нуля, и система имеет только нулевое решение. Наконец, из того же условия . Ее определитель пропорционален определителю Вандермонда n-ro порядка, который отличен от нуля, и система имеет только нулевое решение. Наконец, из того же условия  следует, что следует, что  . Значит, . Значит,  и лемма доказана. и лемма доказана.
Теорема 1.2. Функции линейно независимы и образуют базис в пространстве сплайнов
линейно независимы и образуют базис в пространстве сплайнов 
Доказательство. Покажем сначала линейную независимость функций на всей действительной оси. Предположим противное, т. е. что существуют такие постоянные на всей действительной оси. Предположим противное, т. е. что существуют такие постоянные  , не все равные нулю, что , не все равные нулю, что

Выбирая получаем, что получаем, что и, значит, и, значит,  . Беря затем . Беря затем  находим, что находим, что  и т.д., т.е. и т.д., т.е.  Следовательно, функции Следовательно, функции  линейно независимы на линейно независимы на 
Предположим теперь, что соотношение (8) выполняется только на [а, b]. Это значит, что на отрезках  обращаются в нули сплайны вида обращаются в нули сплайны вида

Каждый из них отличен от нуля самое большее на интервале  Поэтому из предположения Поэтому из предположения  при x при x согласно доказательству леммы 3 следует, что согласно доказательству леммы 3 следует, что  0 на интервалах 0 на интервалах  , а значит, и на всей действительной оси. В силу линейной независимости функций , а значит, и на всей действительной оси. В силу линейной независимости функций  на на должно быть должно быть  и это для всех i = 0, ..,N-1. и это для всех i = 0, ..,N-1.
Таким образом, функции линейно независимы, и так как согласно теореме 1.1 размерность пространства линейно независимы, и так как согласно теореме 1.1 размерность пространства равна n+N, то они образуют базис в этом пространстве. Теорема доказана. равна n+N, то они образуют базис в этом пространстве. Теорема доказана.
Функции  называются базисными сплайнами с конечными носителями минимальной длины (В-сплайнами). В силу теоремы 1.2 всякий сплайн называются базисными сплайнами с конечными носителями минимальной длины (В-сплайнами). В силу теоремы 1.2 всякий сплайн может быть единственным образом записан может быть единственным образом записан

где — некоторые постоянные коэффициенты. Эту запись сплайна называют его представлением через В-сплайны.
Из теоремы 1.2 вытекает
Следствие 1.1. Всякий сплайн , принадлежащий , принадлежащий  , с конечным носителем минимальной длины с точностью до постоянного множителя совпадает с В-сплайном. , с конечным носителем минимальной длины с точностью до постоянного множителя совпадает с В-сплайном.
Доказательство. Минимальным конечным носителем сплайна является один из интервалов   Согласно (9) Согласно (9)

Так как 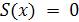 для для 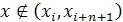 то, выбирая последовательно то, выбирая последовательно 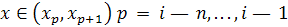 , получаем, что , получаем, что 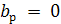 . Аналогично, . Аналогично, 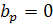 для для 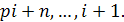 Следовательно, Следовательно, 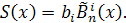
Замечание. Представление сплайнов через B-сплайпы в виде (9) имеет смысл для конечного отрезка [а, b]. Чтобы получить его для всей вещественней оси, нужно положить 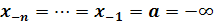 и и 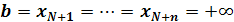 . Тогда точки . Тогда точки 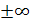 оказываются узлами кратности оказываются узлами кратности 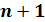 и при построении B-сплайнов с номерами и при построении B-сплайнов с номерами 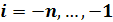 и и 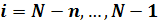 нужно учитывать правило для разделенных разностей с кратными узлами. Мы не описываем подробно эти конструкции, ибо все практические задачи, где используются B-сплайны, рассматриваются на конечном отрезке. нужно учитывать правило для разделенных разностей с кратными узлами. Мы не описываем подробно эти конструкции, ибо все практические задачи, где используются B-сплайны, рассматриваются на конечном отрезке.
При практических вычислениях удобнее использовать не сами B-сплайны, а функции, получающиеся из них умножением на постоянные множители:
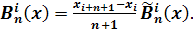 (1) (1)
Эти функции называются нормализованными В-сплайнами. Нормирующий множитель равен среднему арифметическому шагов  на отрезке, где B-сплайн отличен от нуля. на отрезке, где B-сплайн отличен от нуля.
Тождество (2.4) для нормализованных 5-сплайнов имеет вид

С его помощью легко можно построить последовательность сплайнов  Приведем первые четыре функции этой последовательности для случая равноудаленных узлов hi
= h. Приведем первые четыре функции этой последовательности для случая равноудаленных узлов hi
= h.
Будем обозначать Точка Точка - это середина отрезка-носителя В-сплайна. Тогда имеем - это середина отрезка-носителя В-сплайна. Тогда имеем

Эти В-сплайны изображены на рис. 1.3, а, б, в, г соответственно.
В § 1 было отмечено, что многочлены Рп
(х) степени не выше n являются элементами пространства сплайнов  .
Следовательно, они представимы через базисы этих пространств, в частности через базис из В-сплайнов в пространстве .
Следовательно, они представимы через базисы этих пространств, в частности через базис из В-сплайнов в пространстве  . Для вывода формул воспользуемся тождеством (2). После умножения обеих его частей на число и суммирования по индексу i получаем . Для вывода формул воспользуемся тождеством (2). После умножения обеих его частей на число и суммирования по индексу i получаем

Лемма 1.4. Справедливо тождество

в предположении 

Доказательство. В формуле (4) положим  Тогда получаем Тогда получаем

Подставляя  в (3), находим в (3), находим

Повторяя это преобразование n раз, получим справа

Теперь разложим обе части тождества (5) по степеням t. При этом

Здесь  суть символы элементарных симметрических функций от n аргументов степени а. Это многочлены, состоящие из суть символы элементарных симметрических функций от n аргументов степени а. Это многочлены, состоящие из  слагаемых. Они имеют вид слагаемых. Они имеют вид
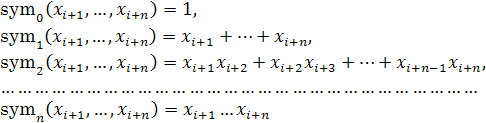
Подставляя разложения (6) и (7) в (5) и приравнивая коэффициенты при одинаковых степенях t, находим представления мономов 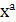 через нормализованные В-сплайны па отрезке через нормализованные В-сплайны па отрезке 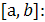

В частности, при а = 0 получаем соотношение

которое для нормализованных 5-сплайпов играет ту же роль, что свойство (2.6) для самих 5-сплайнов.
Полученные формулы (8) решают вопрос о представлении произвольного многочлена п-й степени через нормализованные В-сплайны.
В данной работе мы рассмотрели понятие сплайна и основные определения необходимые для работы с ним. Было изучено понятие базисного сплайна или B-сплайна, а так же уделено внимание его форме в виде нормализованного сплайна. Так же была создана программа для интерполяции сплайнов при помощи языка программирования высокого уровня C++.
1. Вержбицкий В.М. Основы численных методов – М.:Высш. шк., 2002.
2. Завьялов Ю.С., Квасов Б.И., Мирошниченко В.Л. Методы сплайн – функций - М.: Наука, 1980. 352 с
3. Бахвалов Н. С., Жидков Е. П., Кобельков Г. М. Численные методы. Учебное пособие. - 4-е издание – М.- СПб.: Физматлит, Невский диалект, Лаборатория базовых знаний, 2003
4. Препарата Ф., Шеймос М. Вычислительная геометрия. Введение. - Мир, 1989
5. Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа - М.: Наука, 1976
Листинг программы.
#include<conio.h>
#include<iostream>
using namespace std;
double KubichSplain ( int n, double *X, double *Y, double Xp )
{
double *Q, *L, *A, *B, *C, *D, DXp, Yp;
int i, j, k;
Q = new double [n];
L = new double [n];
A = new double [n];
B = new double [n];
C = new double [n];
D = new double [n];
for(i=0;i<n;i++)
if(Xp<=X[i])
{
k=i;
break;
}
Q[1] = (-1) * (X[2]-X[1])/2*(X[1]-X[0] + X[2]-X[1]);
L[1] = (3*(Y[2]-Y[1])/(X[2]-X[1]) - 3*(Y[1]-Y[0])/(X[1]-X[0])) / (2*(X[1]-X[0] + X[2]-X[1]));
C[n-1]=0;
C[0]=0;
for(i=3; i<n; i++)
{
Q[i-1]=(-1) * (X[i]-X[i-1]) / (2*(X[i-1]-X[i-2]+X[i]-X[i-1])+(X[i-1]-X[i-2])*Q[i-2]);
L[i-1]=(3*((Y[i]-Y[i-1])/(X[i]-X[i-1])-(Y[i-1]+Y[i-2])/
(X[i-1]-X[i-2]))-(X[i-1]-X[i-2])*L[i-2])/(2*(X[i-1]-X[i-2]+X[i]-X[i-1])+(X[i-1]-X[i-2])*Q[i-2]);
}
for(i=n-1; i>=2; i--)
C[i-1]=Q[i-1]*C[i]+L[i-1];
A[0]=Y[0];
for(i=1;i<n;i++)
{
A[i]=Y[i];
D[i]=(C[i]-C[i-1])/3.*(X[i]-X[i-1]);
B[i]=(Y[i]-Y[i-1])/(X[i]-X[i-1])+2.*(X[i]-X[i-1])*C[i]/3.+(X[i]-X[i-1])*C[i-1]/3.;
}
DXp=Xp-X[k];
//получение значения интерполирующей функции
Yp = A[k] + B[k]*DXp + C[k]*DXp*DXp + D[k]*DXp*DXp*DXp;
delete []A;
delete []B;
delete []C;
delete []D;
delete []Q;
delete []L;
return Yp;
}
void main ( void )
{
double *X, *Y, Xp;
int n, i;
system("CLS");
cout << "Enter n: ";
cin >> n;
X = new double [n];
Y = new double [n];
for ( i = 0; i < n; i ++ )
{
cout << "X[ " << i+1 << " ] = ";
cin >> X[i];
}
for ( i = 0; i < n; i ++ )
{
cout << "Y( " << X[i] << " ) = ";
cin >> Y[i];
}
cout << "Xp = ";
cin >> Xp;
cout << "Y( " << Xp << " ) = " << KubichSplain ( n, X, Y, Xp )<<"\n";
getch();
delete []X;
delete []Y;
}
|