| Уточнение простой теории МО ЛКАО.
Базисная АО. Эффективный заряд-показатель экспоненты
Образование молекулярного иона водорода удобно рассматривать в качестве лишь промежуточной стадии в идеализированном адиабатическом процессе слияния протона с атомом водорода: 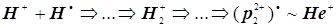
Суммарное электростатическое поле двух сближающихся протонов постепенно пре-вращается в поле гипотетического объединённого точечного заряда , заряд которого равен заряду двух протонов, т.е. Z=+2 а.е.. Точно такое же поле создаёт ядро атома гелия , заряд которого равен заряду двух протонов, т.е. Z=+2 а.е.. Точно такое же поле создаёт ядро атома гелия 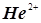 , от которого гипотетическое объединение двух протонов , от которого гипотетическое объединение двух протонов  отличается отсутствием двух нейтронов, необходимых для существования стабильного ядра. Во всяком случае электростатическое поле гипотетической протонной пары не должно отличаться от поля реального ядра атома гелия. отличается отсутствием двух нейтронов, необходимых для существования стабильного ядра. Во всяком случае электростатическое поле гипотетической протонной пары не должно отличаться от поля реального ядра атома гелия.
Образование молекулярной орбитали основного энергетического уровня молекулярного иона водорода 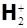 формально является промежуточной стадией трансформации электронного состояния в процессе адиабатического слияния двух 1s(H)-АО в поле раздельных протонов в одну 1s(He+)-АО, но уже в поле объединённого ядра. Отсюда вытекает один из очень плодотворных способов улучшения пробной волновой функции трёхчастичной системы в основном состоянии. Базисные волновые функции, вначале выбранные как 1s -АО атома водорода вида формально является промежуточной стадией трансформации электронного состояния в процессе адиабатического слияния двух 1s(H)-АО в поле раздельных протонов в одну 1s(He+)-АО, но уже в поле объединённого ядра. Отсюда вытекает один из очень плодотворных способов улучшения пробной волновой функции трёхчастичной системы в основном состоянии. Базисные волновые функции, вначале выбранные как 1s -АО атома водорода вида
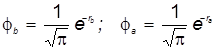 заменяются атомными орбиталями водородоподобного типа, заменяются атомными орбиталями водородоподобного типа,
которые лишаются привычного физического смысла, превращаясь просто в средство математического расчёта электронных свойств молекулы. При этом в показатель экспоненты вместо истинного заряда ядра Z вводится эффективный варьируемый «заряд ядра» Предельные значения этой новой дополнительной переменной известны: 1< <2. Это заряды ядер атомов водорода и гелия. Нормированные базисные функции это уже псевдо-АО (поскольку атомы с промежуточными зарядами ядер не существуют), которые имеют вид:
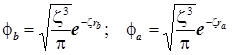 . (7) . (7)
В этом случае полная энергия рассматривается уже как оптимизируемая функция уже двух варьируемых переменных: межъядерного расстояния R и эффективного показателя экспоненты - . Их оптимальные значения соответствуют абсолютному минимумуму полной энергии.
Необходимо вычислить энергию в зависимости не только от межъядерного расстояния, но и от эффективного заряда ядра - показателя экспоненты базисной АО ., т.е.:
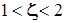 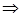 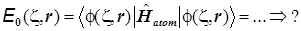 ; ;
Проследим все вычисления с самого начала, и необходимые уточнения, связанные с коррекцией базисной АО появляются автоматически как простое следствие более внимательного расчёта.
1.Уровни энергии МО представляют собою собственные числа гамильтониана.
Их средние значения определятся общим уравнением:
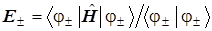 , ( 8 ) , ( 8 )
а если волновые функции МО предварительно были нормированы, то
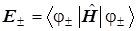 ( 9 ) ( 9 )
Волновые функции МО имеют вид линейных комбинаций.
Подставим выражение волновой функции МО в формулу энергии. На первой стадии выясним конструкцию получающихся формул, не раскрывая гамильтониан.
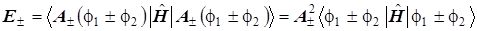 , ( 10 ) , ( 10 )
т.е. 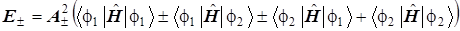 , ( 11 ) , ( 11 )
Выражение для энергия оказалась билинейной формой (9, 11). Её слагаемые возникли как парные комбинации базисных элементов - АО, составляющих МО, т.е. они оказываются элементами двумерного массива - матрицы. Подобную конструкцию обычно имеют многие выражения квантовой механики и квантовой химии.
Молекулярный гамильтониан сам представляет собою также сумму нескольких слагаемых, и поэтому каждый его матричный элемент также распадается на такое же число отдельных слагаемых. В результате, следуя формуле (9), энергия оказывается суммой слагаемых, число которых равно произведению чисел b h k, первое из которых bэто число слагаемых бра-вектора, второе h - гамильтониана, третье k - кет-вектора.
В нашем случае (b, h, k)= (2, 3, 2), так что энергия состоит из двенадцати слагаемых.
Для определённости следует индексами указать происхождение каждого из них, т.е. пару базисных АО и то слагаемое гамильтониана, от которого они произошли.
3. Матричные элементы молекулярного гамильтониана.
Матричные элементы гамильтониана суть
 ( 12 ) ( 12 )
Они между собою попарно равны, а именно:
-диагональные 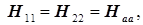
-недиагональные 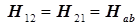 . .
4. Энергетические уровни.
Энергия равна 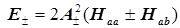 , и получается выражение для двух уровней: , и получается выражение для двух уровней:
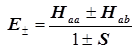 ( 13 ) ( 13 )
Цель всех расчётов дать читателю возможность осуществить компьютерно-графическое моделирование основных молекулярных характеристик.
Атомное и двуцентровые слагаемые молекулярного гамильтониана -
матричные элементы гамильтониана
а) диагональный элемент имеет вид суммы трёх слагаемых: 
 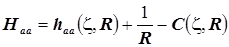 . ( 14 ) . ( 14 )
б) недиагональный элемент также распадается на три слагаемых. При этом Hba
= Hab
:
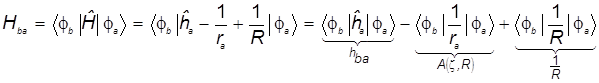 . (15 ) . (15 )
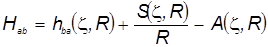 . ( 16 ) . ( 16 )
Вначале подойдём ко всем одноэлектронным молекулярным интегралам просто как к параметрам, не раскрывая их. Вычислим их в явном виде чуть далее.
Энергетические уровни и молекулярные интегралы
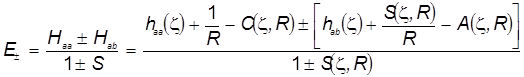 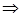
Выражение для энергии представим в симметричном виде, а именно:
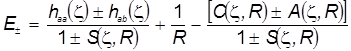 а.е. (17 ) а.е. (17 )
В этой формуле в числителе первой дроби представлены матричные элементы одноцентрового оператора 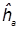 . По своему виду он совпадает с электронным гамильтонианом водородоподобного атома (иона), но следует помнить, что такой оператор искусственно выделен лишь как одно из удобных слагаемых в молекулярном гамильтониане, и поэтому всё, что с ним связано, выделено просто соображениями математического и классификационного удобства. . По своему виду он совпадает с электронным гамильтонианом водородоподобного атома (иона), но следует помнить, что такой оператор искусственно выделен лишь как одно из удобных слагаемых в молекулярном гамильтониане, и поэтому всё, что с ним связано, выделено просто соображениями математического и классификационного удобства.
Рассчитанные энергетические уровни МО этой простейшей одноэлектронной молекулы включают лишь те компоненты энергии, которые были учтены в гамильтониане, а именно: кинетическую энергию электрона, движущегося в поле обоих ядер, потенциальную энергию его электростатического (кулоновского) притяжения к обоим ядрам и потенциальную энергию взаимного кулоновского отталкивания ядер. Кинетическая энергия ядер в составленном нами гамильтониане отсутствует, и потому она не включена и в рассчитанные уровни
МО, которые в этом виде не совпадают с полной энергией системы в каждом из состояний. Отличие невелико (всего-навсего на величину энергии взаимных периодических движений ядер - колебаний ядерного остова молекулы), и всё же о нём не следует забывать. Для такого напоминания пригодно и само название. Поэтому полученные энергетические функции,
рассчитанные в приближении фиксированных ядер называют адиабатическими потенциалами. Устойчивым состояниям молекул отвечают лишь такие адиабатические потенциалы, у которых имеются один или несколько минимумов. Они-то и представляют интерес в первую очередь.
Согласно теоретической модели метода МО ЛКАО уровни (адиабатические потенциалы) выражены с помощью нескольких одноэлектронных молекулярных интегралов:
1)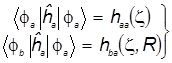
2) 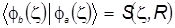 - интеграл перекрывания - интеграл перекрывания
3)  - кулоновский интеграл - кулоновский интеграл
4) 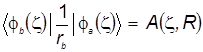 - обменный интеграл (18) - обменный интеграл (18)
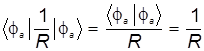 -энергия электростатического отталкивания ядер -энергия электростатического отталкивания ядер
Нормированные молекулярные орбитали имеют вид:
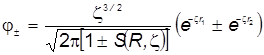 . (19 ) . (19 )
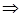 (
=1
) (
=1
) 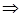
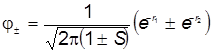 . (20 ) . (20 )
Предварительно введём несколько вспомогательных формул,
необходимых
для расчёта числовых значений специальных несобственных интегралов вида:
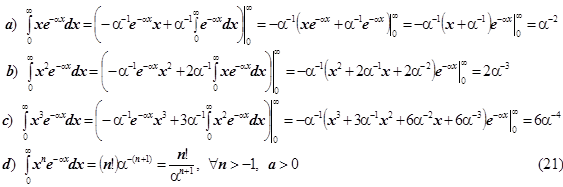
Расчёт энергетические уровни МО
(с варьированием показателя экспоненты базисных водородоподобных АО).
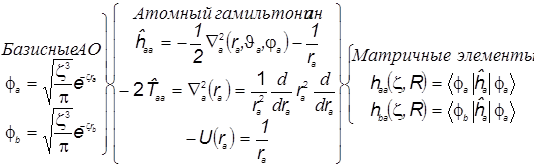 . (22 Напомним, что в шаровых координатах лапласиан имеет вид . (22 Напомним, что в шаровых координатах лапласиан имеет вид
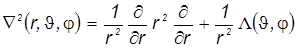 . ( 23 ) . ( 23 )
Поскольку выбранные нами базисные s-АО не зависят от угловых переменных, то и результат действия на них угловой части лапласиана, составляющей оператор Лежандра, нулевой. Поэтому имеет смысл в выкладках оставить лишь радиальную часть лапласиана, а соответственно, символ частного дифференцирования следует заменить символом полного дифференцирования по единственной оставшейся переменной r
.
Вычисление матричных элементов одноцентрового
(атомного) гамильтониана
1) Диагональные матричные элементы
haa
=
hbb
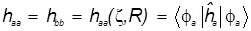 . ( 24 ) . ( 24 )
Нижний индекс в данном пункте расчёта удобно опустить.
Слагаемое 1
(порождено потенциальным слагаемым атомного гамильтониана):
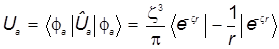 . ( 25 ) . ( 25 )
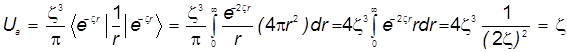 ; ( 26) ; ( 26)
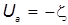 . (27) . (27)
Слагаемое 2
(порождено кинетическим слагаемым атомного гамильтониана):
Это слагаемое рассчитывается по формуле:
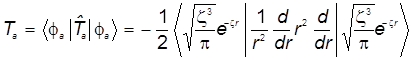 . (28) . (28)
а) Заменим дифференциальные операции более простыми выражениями. Для этого рассмотрим преобразуем волновую функцию, следуя операторному уравнению : :
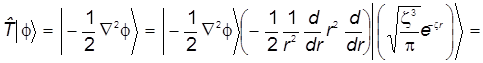
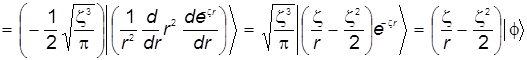 . (29) . (29)
Из последней цепочки равенств следует координатное выражение атомного оператора кинетической энергии. Опуская в ней промежуточные и оставляя лишь начальное и конечное выражения, приходим к привычной форме операторного уравнения:
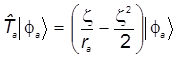 . (30) . (30)
б) Умножая последнее равенство слева на бра-вектор, получаем искомые кинетические слагаемые и диагонального и недиагонального матричных элементов атомного гамильтониана:
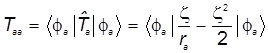 , (31) , (31)
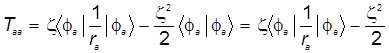 . (32) . (32)
Учитывая нормировку АО 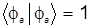 , а также принимая во внимание равенство , а также принимая во внимание равенство
 , получаем: , получаем: 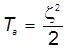 . (33) . (33)
Диагональный матричный элемент одноцентрового гамильтониана получается суммированием потенциального и кинетического слагаемых. Он не зависит от межъядерного расстояния:
 . ( 34) . ( 34)
2) Недиагональные матричные элементы
hab
=
hba
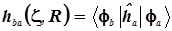 . (35) . (35)
Здесь уже постоянно встречаются оба индекса, и в отличие от расчётов диагонального матричного элемента их опускать нельзя.
Слагаемое 1
(Порождено потенциальной частью одноцентрового гамильтониана)
Это уже знакомый одноэлектронный резонансный
интеграл:
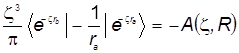 . ( 36 ) . ( 36 )
Для расчёта одноэлектронных двуцентровых интегралов необходимо перейти к двуцентровой эллиптической системе координат.
Слагаемое 2
(Порождено кинетической частью одноцентрового гамильтониана)
а) Используем полученное выше выражение для 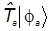 и получаем и получаем
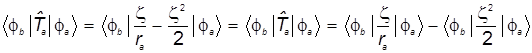 
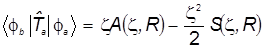
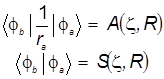 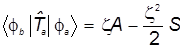 (37 ) (37 )
Результат - весь недиагональный матричный элемент атомного гамильтониана:
Суммируя потенциальное и кинетическое слагаемые, получаем недиагональный матричный элемент атомного гамильтониана. Он зависит и от показателя экспоненты, и от межъядерного расстояния:
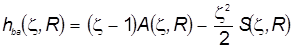 . (38 ) . (38 )
Для расчёта интегралы S
,
C
,
A
следует перевести в двуцентровую систему координат.
Двуцентровые эллиптические (сфероидальные)координаты
Для расчёта необходимы переменные, позволяющие вычислить молекулярные интегралы. В данной задаче такие естественные пространственные переменные возникают в двуцентровой системе координат. В ней всякий эллипсоид вращения характеризуется условием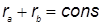 , и всякий гиперболоид вращения - условием , и всякий гиперболоид вращения - условием 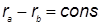 . Центрированные в одних и тех же полюсах системы эллипсоидов и гиперболоидов образуют совокупности взаимно перпендикулярных поверхностей. Это означает, что в любой точке пространства касательные плоскости к пересекающимся эллипсоиду и гиперболоиду взаимно перпендикулярны. . Центрированные в одних и тех же полюсах системы эллипсоидов и гиперболоидов образуют совокупности взаимно перпендикулярных поверхностей. Это означает, что в любой точке пространства касательные плоскости к пересекающимся эллипсоиду и гиперболоиду взаимно перпендикулярны.
В декартовых координатах пространство разбито на элементы системой взаимно ортогональных плоскостей, а в эллиптической - системами концентрических эллипсоидов, гиперболоидов и пучком плоскостей, пересекающихся на оси вращения.
Всякая точка в декартовых координатах вписана в элемент объёма, ограниченный шестью плоскостями, по две вдоль каждой из трёх взаимно перпендикулярных осей координат.
В эллиптических координатах точка ограничена: “сверху и снизу” - двумя эллипсоидами вращения, “с торцов” - двумя гиперболоидами вращения, “по бокам” - двумя плоскостями, пересекающимися на оси вращения. Ядра молекулы расположены в полюсах координатных поверхностей второго порядка. В каждой вершине пространственного элемента плоскости, касательные к координатным поверхностям, взаимно перпендикулярны, но элемент пространства изначально не является прямоугольным параллелепипедом, и потому его элементарный объём рассчитывается не просто как произведение дифференциалов координат. Формула для его вычисления окажется сложнее и должна учитывать искривление координатных поверхностей.
Вычисление элемента объёма в эллиптических переменных
|