БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Кафедра информатики
РЕФЕРАТ
на тему:
«Построение эйлерова цикла. Алгоритм форда и Уоршелла»
МИНСК, 2008
1.
Эйлеровы цепи и циклы
Рассматриваемая задача является одной из самых старейших в теории графов. В городе Кенигсберге (ныне Калининград) имелось семь мостов, соединяющих два берега реки Преголь, и два основа на ней друг с другом (рис. 1а). Требуется, начав путешествие из одной точки города пройти по всем мостам по одному разу и вернуться в исходную точку.
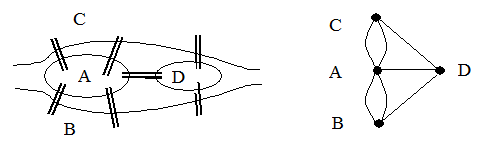
а) б)
Рис. 1.
Если поставить в соответствие мостам ребра, а участкам суши — вершины, то получится граф (точнее псевдограф), в котором надо найти простой цикл, проходящий через все ребра. В общем виде эта задача была решена Эйлером в 1736 г.
Определение 1.
Эйлеровой цепью
в неориентированном графе G
называется простая цепь, содержащая все ребра графа G
. Эйлеровым циклом
называется замкнутая Эйлерова цепь. Аналогично, эйлеров путь
в орграфе G
— это простой путь, содержащий все дуги графа G
. Эйлеров контур
в орграфе G
— это замкнутый эйлеров путь. Граф, в котором существует эйлеров цикл, называется эйлеровым
.
Простой критерий существования эйлерова цикла в связном графе дается следующей теоремой.
Теорема 1.
(Эйлер) Эйлеров цикл в связном неориентированном графе G
(X
, E
) существует только тогда, когда все его вершины имеют четную степень.
Доказательство. Необходимость.
Пусть m - эйлеров цикл в связном графе G
, x
— произвольная вершина этого графа. Через вершину x
эйлеров цикл проходит некоторое количество k
(k
³1) раз, причем каждое прохождение, очевидно, включает два ребра, и степень этой вершины равна 2k
, т.е. четна, так как x
выбрана произвольно, то все вершины в графе G
имеют четную степень.
Достаточность.
Воспользуемся индукцией по числу m
ребер графа. Эйлеровы циклы для обычных (не псевдо) графов можно построить начиная с m
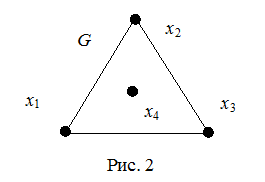
=3.Легко проверить, что единственный граф с m
=3, имеющий все вершины с четными степенями, есть граф K
3
(рис. 2). Существование эйлерова цикла в нем очевидно. Таким образом, для m
=3 достаточность условий доказываемой теоремы имеет место. Пусть теперь граф G
имеет m
>3 ребер, и пусть утверждение справедливо для всех связных графов, имеющих меньше, чем m
ребер. Зафиксируем произвольную вершину a
графа G
и будем искать простой цикл, идущий из a
в a
. Пусть m(a
, x
) — простая цепь, идущая из a
в некоторую вершину x
. Если x
¹a
, то цепь m можно продолжить из вершины x
в некотором направлении. Через некоторое число таких продолжений мы придем в вершину z
ÎX
, из которой нельзя продлить полученную простую цепь. Легко видеть, что z
= a
так как из всех остальных вершин цепь может выйти (четные степени!); a
в a
она начиналась. Таким образом, нами построен цикл m, идущий из a
в a
. Предположим, что построенный простой цикл не содержит всех ребер графа G
. Удалим ребра, входящие в цикл m, из графа G
и рассмотрим полученный граф 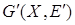 . В графе . В графе 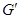 все вершины имеют четные степени. Пусть все вершины имеют четные степени. Пусть 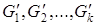 — компоненты связности графа — компоненты связности графа 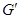 , содержащие хотя бы по одному ребру. Согласно предположению индукции все эти компоненты обладают эйлеровыми циклами m1
, m1
, …, mk , содержащие хотя бы по одному ребру. Согласно предположению индукции все эти компоненты обладают эйлеровыми циклами m1
, m1
, …, mk
 соответственно. Так как граф G
связан, то цепь m встречает каждую из компонент соответственно. Так как граф G
связан, то цепь m встречает каждую из компонент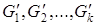 . Пусть первые встречи цикла m с компонентами . Пусть первые встречи цикла m с компонентами 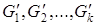 происходят соответственно в вершинах x
1
, x
2
, …, xk
. Тогда простая цепь происходят соответственно в вершинах x
1
, x
2
, …, xk
. Тогда простая цепь
 n(a
, a
)=m(a
, x
1
) Um1
(x
1
, x
1
) Um(x
1
, x
2
) U…Umk
(xk
, xk
) Um(xk
, a
) n(a
, a
)=m(a
, x
1
) Um1
(x
1
, x
1
) Um(x
1
, x
2
) U…Umk
(xk
, xk
) Um(xk
, a
)
является эйлеровым циклом в графе G
. Теорема доказана.
Замечание.
Очевидно, что приведенное доказательство будет верно и для псевдографов, содержащих петли и кратные ребра (см. рис. 1,а).
Таким образом, задача о кенигсбергских мостах не имеет решения, так как соответствующий граф (см. рис. 1,б) не имеет эйлерова цикла из-за нечетности степеней все вершин.
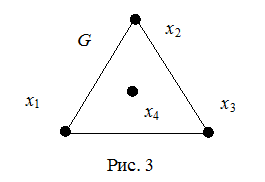 Отметим, что из существования эйлерова цикла в неориентированном графе G
не следует связность этого графа. Например, неориентированный граф G
на рис. 3 обладает эйлеровым циклом и вместе с тем несвязен. Отметим, что из существования эйлерова цикла в неориентированном графе G
не следует связность этого графа. Например, неориентированный граф G
на рис. 3 обладает эйлеровым циклом и вместе с тем несвязен.
Совершенно также, как теорема 1, могут быть доказаны следующие два утверждения.
Теорема 2.
Связный неориентированный граф G
обладает эйлеровой цепью тогда и только тогда, когда число вершин нечетной степени в нем равно 0 или 2, причем если это число равно нулю, то эйлерова цепь будет являться и циклом.
Теорема 3.
Сильно связный орграф G
(X
, E
) обладает эйлеровым контуром тогда и только тогда, когда для любой вершины x
ÎX
выполняется
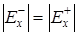 . .
Можно также обобщить задачу, которую решал Эйлер следующим образом. Будем говорить что множество не пересекающихся по ребрам простых цепей 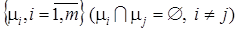 графа G
покрывает
его, если все ребра графа G
включены в цепи mi
. Нужно найти наименьшее количество таких цепей, которыми можно покрыть заданный граф G
. графа G
покрывает
его, если все ребра графа G
включены в цепи mi
. Нужно найти наименьшее количество таких цепей, которыми можно покрыть заданный граф G
.
Если граф G
— эйлеров, то очевидно, что это число равно 1. Пусть теперь G
не является эйлеровым графом. Обозначим через k
число его вершин нечетной степени. По теореме … k
четно. Очевидно, что каждая вершина нечетной степени должна быть концом хотя бы одной из покрывающих G
цепей mi
. Следовательно, таких цепей будет не менее чем k
/2. С другой стороны, таким количеством цепей граф G
покрыть можно. Чтобы убедиться в этом, расширим G
до нового графа 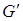 , добавив k
/2 ребер , добавив k
/2 ребер 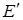 , соединяющих различные пары вершин нечетной степени. Тогда , соединяющих различные пары вершин нечетной степени. Тогда 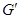 оказывается эйлеровым графом и имеет эйлеров цикл оказывается эйлеровым графом и имеет эйлеров цикл 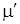 . После удаления из . После удаления из 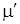 ребер ребер 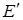 граф разложится на k
/2 цепей, покрывающих G
. Таким образом, доказана. граф разложится на k
/2 цепей, покрывающих G
. Таким образом, доказана.
Теорема 4.
Пусть G
— связный граф с k
>0 вершинами нечетной степени. Тогда минимальное число непересекающихся по ребрам простых цепей, покрывающих G
, равно k
/2.
Для начала отметим, что теорема 1 также дает метод построения эйлерова цикла. Здесь мы рассмотрим несколько иной алгоритм.
Пусть G
(X
, E
) — связный неорентированный граф, не имеющий вершин нечетной степени. Назовем мостом такое ребро, удаление которого из связного графа разбивает этот граф на две компоненты связности, имеющие хотя бы по одному ребру.
1°. Пусть a
— произвольная вершина графа G
. Возьмем любое ребро e
1
=(a
, x
1
) , инцидентное вершине a, и положим m = {e
1
}.
2°. Рассмотрим подграф G
1
(X
, E\
m1
). Возьмем в качестве e
2
ребро, инцидентное вершине x
1
и неинцидентное вершине a
, которое также не является мостом в подграфе G
1
(если такое ребро e
2
существует!). Получим простую цепь m2
= {e
1
, e
2
}.
3°. Пусть e
2
= (x
1
, x
2
), x
¹a
. Рассмотрим подграф G
2
(X
, E\
m2
) и удалим из него все изолированные вершины. В полученном подграфе 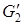 выберем ребро e
3
ÎE
\
m2
, инцидентное вершине a
, которое не является мостом в подграфе выберем ребро e
3
ÎE
\
m2
, инцидентное вершине a
, которое не является мостом в подграфе 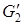 (если такое ребро e
3
существует!). Получим простую цепь (если такое ребро e
3
существует!). Получим простую цепь
m3
= {e
1
, e
2
, e
3
}.
Продолжая указанный процесс, мы через конечное число шагов получим эйлеров цикл m = {e
1
, e
2
, …, en
}, где n
— число ребер графа G
(X
, E
).
Предположим, что уже построена простая цепь mk
-1
= {e
1
, e
2
, …, ek
-1
} для k
³2 методом, указанным в алгоритме. Пусть ek
-1
= (xk
-2
, xk
-1
) и xk
-1
¹a
. Рассмотрим подграф 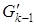 , который получается из подграфа G
k
-1
(X
, E\
mk
-1
) удалением всех изолированных вершин. Вершина xk
-1
в этом подграфе , который получается из подграфа G
k
-1
(X
, E\
mk
-1
) удалением всех изолированных вершин. Вершина xk
-1
в этом подграфе 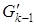 имеет нечетную степень, поэтому существует по крайней мере одно ребро ek
ÎE\
mk
-1
, инцидентное xk
-1
. Если это ребро единственное, то оно не является мостом в графе имеет нечетную степень, поэтому существует по крайней мере одно ребро ek
ÎE\
mk
-1
, инцидентное xk
-1
. Если это ребро единственное, то оно не является мостом в графе 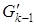 . В противном случае вершина a
будет связана с некоторой вершиной . В противном случае вершина a
будет связана с некоторой вершиной 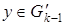 единственной цепью, содержащей ребро ek
, что противоречит существованию эйлерова цикла в графе G
. Поскольку ek
- не мост, то процесс можно продолжать, взяв единственной цепью, содержащей ребро ek
, что противоречит существованию эйлерова цикла в графе G
. Поскольку ek
- не мост, то процесс можно продолжать, взяв 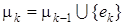 . Если ребро ek
не единственное инцидентное вершине xk
-1
, то среди этих ребер есть по крайней мере одно, не являющееся мостом. В противном случае один из этих мостов . Если ребро ek
не единственное инцидентное вершине xk
-1
, то среди этих ребер есть по крайней мере одно, не являющееся мостом. В противном случае один из этих мостов 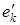 можно выбросить так, что вершины xk
-1
и a
попадут в разные компоненты связности графа можно выбросить так, что вершины xk
-1
и a
попадут в разные компоненты связности графа 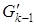 . Если xk
-1
принадлежит компоненте M
, то в этой компоненте все вершины имеют четную степень, поэтому существует эйлеров цикл в M
, проходящий через xk
-1
. Этот цикл содержит все ребра, инцидентные xk
-1
и принадлежащие . Если xk
-1
принадлежит компоненте M
, то в этой компоненте все вершины имеют четную степень, поэтому существует эйлеров цикл в M
, проходящий через xk
-1
. Этот цикл содержит все ребра, инцидентные xk
-1
и принадлежащие 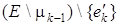 , являющиеся одновременно мостами. Получено противоречие, так как ребра из эйлерова цикла мостами быть не могут. Итак, в рассмотренном случае существует ребро ek
, инцидентное вершине xk
-1
и не являющееся мостом. Значит, и в этом случае процесс можно продолжать, взяв , являющиеся одновременно мостами. Получено противоречие, так как ребра из эйлерова цикла мостами быть не могут. Итак, в рассмотренном случае существует ребро ek
, инцидентное вершине xk
-1
и не являющееся мостом. Значит, и в этом случае процесс можно продолжать, взяв
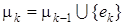 . .
Из предыдущего следует, что процесс нельзя продолжать тогда и только тогда, когда мы попадем в вершину a
, причем степень вершины a
относительно непройденных ребер равна нулю. Докажем, что в этом случае построенный цикл m - простой цикл. Покажем, что m содержит все ребра графа G
. Если не все ребра графа G
принадлежат m, то не принадлежащие m ребра порождают компоненты связности C
1
, …, Cm
(m
³1) в подграфе 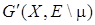 . Пусть компонента Ci
, 1£i
£m
соединяется с циклом m в вершине yi
. Если существует ребро e
Îm , такое, что e
=(yi
, a
), то при построении цикла m было нарушено правило выбора ребра e
, что невозможно. Если часть цикла m, соединяющая yi
и a
, состоит более чем из одного ребра, то первое ребро этой части . Пусть компонента Ci
, 1£i
£m
соединяется с циклом m в вершине yi
. Если существует ребро e
Îm , такое, что e
=(yi
, a
), то при построении цикла m было нарушено правило выбора ребра e
, что невозможно. Если часть цикла m, соединяющая yi
и a
, состоит более чем из одного ребра, то первое ребро этой части 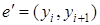 было мостом, и поэтому было нарушено правило выбора было мостом, и поэтому было нарушено правило выбора 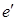 , что невозможно. Итак, непройденных ребер быть не может, поэтому m - эйлеров цикл. , что невозможно. Итак, непройденных ребер быть не может, поэтому m - эйлеров цикл.
2. НАХОЖДЕНИЕ КРАТЧАЙШИХ ПУТЕЙ В ГРАФЕ
Рассматрим ориентированные графы G
(X
, E
) каждой дуге e
ÎE
которого ставится в соответствие вещественное число l
(e
). Т.е. на множестве Е
создана функция l
:E
®R
. Такой граф принято называть нагруженным
. Само число l
называется весом
дуги.
Можно увидеть аналогию между, например, картой автомобильных или железных дорог. Тогда множество вершин Х
будет соответствовать городам, множество дуг – магистралям, соединяющим города, а веса – расстояниям. (На практике, при этом, фактически получится неориентированный граф).
В связи с изложенной аналогией будем называть веса дуг расстояниями.
Определение 2.
1. Пусть имеется последовательность вершин x
0
, x
1
, …, xn
, которая определяет путь в нагруженном графе G
(X
, E
), тогда длина
этого пути определяется как 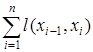 . .
Естественный интерес представляет нахождение кратчайшего
пути между двумя заданными вершинами x и y.
Алгоритм Форда отыскания кратчайшего пути
.
Будем предполагать, что все расстояния в графе положительны. (Если это не так, то ко всем весам можно всегда добавить такую константу, что все эти веса станут положительными).
Пусть мы ищем путь от вершины x
0
к вершине xn
. Будем каждой вершине xi
ставить в соответствие некоторое число li
по следующим правилам.
1° Положим l0
= 0, li
= ¥ (достаточно большое число) для "i
> 0.
2° Ищем в графе дугу (xi
, xj
) удовлетворяющую следующему условию
lj
- li
> l
(xi
, xj
), (1)
после чего заменяем lj
на
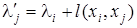 . .
Пункт 2°повторяется до тех пор, пока невозможно будет найти дугу, удовлетворяющую условию (1). Обоснуем этот алгоритм и укажем как определяется кратчайший путь.
Отметим, что ln
монотонно уменьшается, то после завершения алгоритма найдется дуга 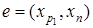 , такая, что
, такая, что 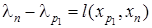 для которой последний раз уменьшалось ln
. (Иначе вообще нет пути между x
0
и xn
или для для которой последний раз уменьшалось ln
. (Иначе вообще нет пути между x
0
и xn
или для 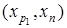 верно (1)). верно (1)).
По этой же самой причине найдется вершина 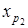 , такая , что
, такая , что
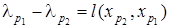 , ,
этот процесс может продолжаться и дальше, так что получится строго убывающая последовательность 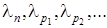 . Отсюда следует, что при некотором k
мы получим . Отсюда следует, что при некотором k
мы получим 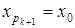 . .
Покажем, что 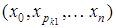 – минимальный путь с длиной ln
, т.е. длина любого другого пути между x
0
и xn
не превышает kn
. – минимальный путь с длиной ln
, т.е. длина любого другого пути между x
0
и xn
не превышает kn
.
Возьмем произвольный путь 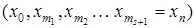 и рассмотрим его длину и рассмотрим его длину 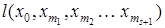 . .
После завершения алгоритма имеем следующие соотношения
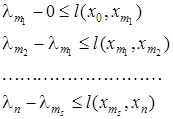
Сложив все эти неравенства, получим
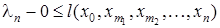 , ,
что и требовалось доказать.
Рассмотрим пример.
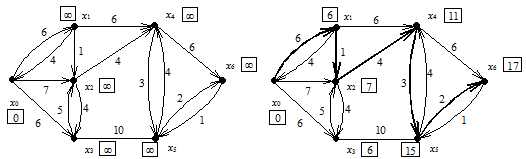 а б а б
Рис. 2.1
На рис. 2.1а изображен исходный помеченный граф и начальные значения li
. На рис. 2.1б для того же графа указаны конечные значения li
и выделен кратчайший путь. Пометка вершин графа происходила в следующем порядке (в скобках указана дуга, вдоль которой выполняется (1)):
l1
= 6 (x
0
, x
1
),
l2
= 7 (x
0
, x
2
),
l3
= 6 (x
0
, x
3
),
l4
= 12 (x
1
, x
3
),
l4
= 11 (x
2
, x
4
),
l5
= 16 (x
3
, x
4
),
l5
= 15 (x
4
, x
5
),
l6
= 18 (x
4
, x
6
),
l6
= 17 (x
5
, x
6
).
Иногда возникает задача отыскания кратчайших расстояний между всеми парами вершин. Одним из способов решения этой задачи является
Алгоритм Флойда
Обозначим lij
длину дуги (xi
, xj
), если таковой не существует примем lij
= ¥, кроме того, положим lii
= 0. Обозначим 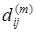 длину кратчайшего из путей из xi
в xj
с промежуточными вершинами из множества {x
1
, …, xm
}. Тогда можно получить следующие уравнения длину кратчайшего из путей из xi
в xj
с промежуточными вершинами из множества {x
1
, …, xm
}. Тогда можно получить следующие уравнения
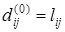 , (2) , (2)
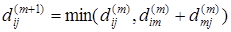 . (3) . (3)
Уравнение (2) очевидно. Обоснуем уравнение (3). Рассмотрим кратчайший путь из xi
в xj
с промежуточными вершинами из множества {x
1
, …, xm
, xm
+1
}. Если этот путь не содержит xm
+1
, то 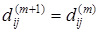 . Если же он содержит xm
+1
, то деля путь на отрезки от xi
до xm
+1
и от xm
+1
до xj
, получаем равенство . Если же он содержит xm
+1
, то деля путь на отрезки от xi
до xm
+1
и от xm
+1
до xj
, получаем равенство 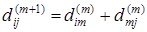 . .
Уравнения (2) и (3) позволяют легко вычислить матрицу расстояний [dij
] между всеми парами вершин графа G
(X
, E
). На первом этапе согласно (2) составляем n
´n
матрицу 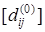 равную матрице [lij
] весов ребер (n
– число вершин G
(X
, E
)). n
раз производим вычисление по итерационной формуле (3), после чего имеем равную матрице [lij
] весов ребер (n
– число вершин G
(X
, E
)). n
раз производим вычисление по итерационной формуле (3), после чего имеем 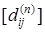 – матрицу расстояний. – матрицу расстояний.
Отметим, что алгоритм Флойда непосредственно не указывает сам кратчайший путь между вершинами, а только его длину. Алгоритм Флойда можно модифицировать таким образом, чтобы можно было находить и сами пути. Для этого получим вспомогательную матрицу [Rij
], которая будет содержать наибольший номер вершины некоторого кратчайшего пути из xi
в xj
(Rij
=0, если этот путь не содержит промежуточных вершин).
Эта матрица вычисляется параллельно с 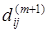 по следующим правилам по следующим правилам
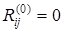
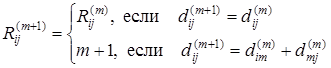 
Последнее выражение следует из обоснования (3).
Теперь кратчайший путь выписывается из следующего рекурсивного алгоритма:
Кратчайший путь из xi
в xj
:
1°. Если Rij
= 0 то выполнить 2°,
иначе выполнить 3°.
2°. Если i
=j
то выписать xi
и закончить,
иначе выписать xi
и xj
закончить.
3°. Выписать кратчайший путь между xi
и 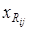 . .
4°. Выписать кратчайший путь между 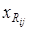 и xj
. и xj
.
Пункты 3° и 4° предполагают рекурсивное обращение к рассмотренному алгоритму.
С задачей определения кратчайших путей в графе тесно связана задача транзитивного замыкания бинарного отношения.
Напомним, что бинарным отношением на множестве Х
называется произвольное подмножество E
ÌX
´X
.
Транзитивным называется отношение, удовлетворяющее следующему условию: если (x
, y
) ÎE
и (y
,
z
) ÎE
, то (x
,
z
) ÎE
для всех x
, y
, z
ÎX
. Отметим, что бинарное отношение можно однозначно представить орграфом G
(X
, E
). Теперь для произвольного отношения Е
определим новое отношение Е
* следующим образом
E
* = {(x
, y
) | если в G
(X
, E
) существует путь ненулевой длины из x
в y
}.
Легко проверить, что Е
* - транзитивное отношение. Кроме того, Е
* является наименьшим транзитивным отношением на Х
в том смысле, что для произвольного транзитивного отношения F
ÉE
выполняется E
* ÉF
. Отношение Е
* называется транзитивным замыканием
отношения Е
.
Если отношение Е
представить в виде графа G
(X
, E
) в котором каждая дуга имеет вес 1, то транзитивное замыкание Е
* можно вычислить с помощью алгоритма Флойда. При этом надо учесть, что
(xi
, xj
) ÎE
* если 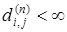 . .
Для большего удобства алгоритм Флойда в этом случае можно модифицировать следующим образом.
Положим
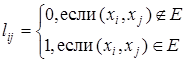 . .
Вместо (3) запишем
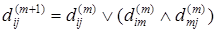 , ,
где Ú – дизъюнкция (логическое сложение),
Ù – конъюнкция (логическое умножение).
После завершения работы алгоритма будем иметь
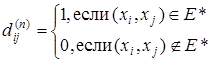
Модифицированный таким образом алгоритм называется алгоритмом Уоршелла.
ЛИТЕРАТУРА
1. Баканович Э.А., Волорова Н.А., Епихин А.В. Дискретная математика:. В 2-х ч..– Мн.: БГУИР, 2000.– 52 с., ил. 14 ISBN 985-444-057-5 (ч. 2).
2. Аттетков А.В., Галкин С.В., Зарубин В.С. Методы оптимизации. М. Иза-во МГТУ им. Н.Э.Баумана, 2003.
3. Белоусов А.И., Ткачев С.Б. Дискретная математика: Учебник для ВУЗов / Под ред. В.С. Зарубина, А.П. Крищенко.– М.: изд-во МГТУ им. Н.Э. Баумана, 2001.– 744 с. (Сер. Математика в техническом университете; Вып XIX).
|