Содержание
Введение
Задание 1
Представить с помощью кругов Эйлера множественное выражение
Используя законы и свойства алгебры множеств, упростить заданное выражение
Задание 2
Заданы множества кортежей
Показать, что эти множества представляют собой соответствия между множествами N1
и N2
, если N1
= N2
= 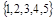 . Дать полную характеристику этих соответствий . Дать полную характеристику этих соответствий
Задание 3
Частично упорядоченное множество М задано множеством упорядоченных пар
Построить диаграмму и определить, является ли данное множество решеткой. Если заданное множество является решеткой, то определить, является ли решетка дедекиндовой , дистрибутивной …
Задание 4
Является ли полной система булевых функций 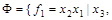 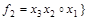 ? Если система функций полная ,то выписать все возможные базисы ? Если система функций полная ,то выписать все возможные базисы
Задание 5
Минимизировать булеву функцию 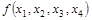 по методу Квайна – Мак-Класки по методу Квайна – Мак-Класки
Задание 6
Для неориентированного графа 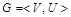 , у которого , у которого 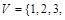 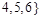 , , 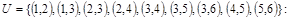
а) вычислить числа 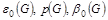 ; ;
б) определить хроматическое число 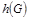 … …
Задание 7
Для заданной сети 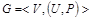 : :
а) найти величину минимального пути и сам путь от вершины 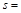 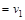 до вершины до вершины 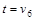 по алгоритму Дейкстры ; по алгоритму Дейкстры ;
б) используя алгоритм Форда-Фалкерсона, определить максимальный поток 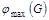 ( v1
– вход , v6
– выход сети ) и указать минимальный разрез, отделяющий v1
от v6
, если задана матрица весов (длин, пропускных способностей) Р… ( v1
– вход , v6
– выход сети ) и указать минимальный разрез, отделяющий v1
от v6
, если задана матрица весов (длин, пропускных способностей) Р…
Литература
Введение
Проблемы, связанные с понятиями бесконечности, дискретности и непрерывности, рассматривались в математике, как и в философии, древнегреческими мыслителями, начиная с 6 века до нашей эры. Под влиянием сочинений Аристотеля они широко обсуждались средневековыми учеными и философами в странах Европы и Азии. Через всю историю математики проходит идея преодоления между актуальной и потенциальной бесконечностью, с одной стороны, между дискретным характером числа и непрерывной природой геометрических величин – с другой. Впервые проблема математической бесконечности и связанных с нею понятий была широко поставлена в наиболее общем виде в теории множеств, основы которой были разработаны в последней четверти 19 века Георгом Кантором.
Цель контрольной работы – ознакомится с основными понятиями и методами решения по дискретной математике, уметь применить полученные знания при решении практического задания.
Задание 1
Представить с помощью кругов Эйлера множественное выражение
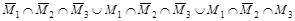 . .
Используя законы и свойства алгебры множеств, упростить заданное выражение.
Решение:
Используя круги Эйлера и, учитывая, что операция пересечения выполняется раньше операции объединения, получим следующие рисунки:
  
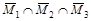 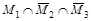 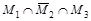
Объединяя заштрихованные области, получим искомое множество:

Упростим заданное выражение:
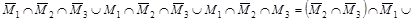
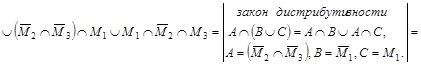
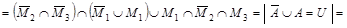
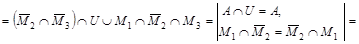
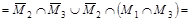 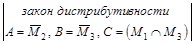 = =
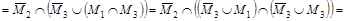
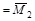 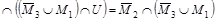 . .
Задание 2
Заданы множества кортежей:
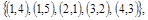
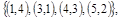
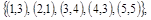
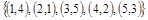 . .
Показать, что эти множества представляют собой соответствия между множествами N1
и N2
, если N1
= N2
= 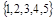 . Дать полную характеристику этих соответствий . Дать полную характеристику этих соответствий
Решение:
Найдем декартово произведение:
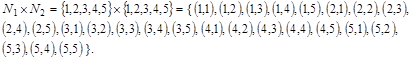
Видно, что заданные множества являются подмножествами этого пря-мого произведения. Следовательно, данные множества есть соответствия.
а) 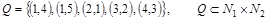 . .

Область определения: 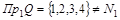 . Следовательно, соответствие является частично определенным. . Следовательно, соответствие является частично определенным.
Область значений: 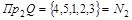 . Следовательно, соответствие является сюръективным. . Следовательно, соответствие является сюръективным.
Образом элемента 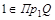 являются два элемента являются два элемента 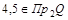 . Значит соответствие не является функциональным. Из этого следует, что соответствие не является функцией, отображением. . Значит соответствие не является функциональным. Из этого следует, что соответствие не является функцией, отображением.
б) 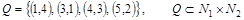 . .
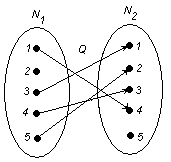
Область определения: 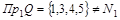 . Следовательно, соответствие является частично определенным. . Следовательно, соответствие является частично определенным.
Область значений: 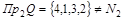 . Следовательно, соответствие не является сюръективным. . Следовательно, соответствие не является сюръективным.
Образом любого элемента из 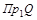 является единственный элемент из является единственный элемент из 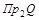 . Следовательно, соответствие является функциональным, функци-ей. Соответствие является частично определенным. Это означает, что функция является частично определенной и не является отображением. . Следовательно, соответствие является функциональным, функци-ей. Соответствие является частично определенным. Это означает, что функция является частично определенной и не является отображением.
в) 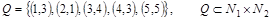 . .
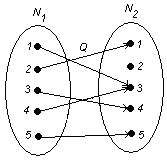
Область определения: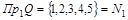 .Следовательно, соответствие всюду определено. .Следовательно, соответствие всюду определено.
Область значений: 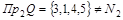 . Следовательно, соответствие не является сюръективным. . Следовательно, соответствие не является сюръективным.
Образом любого элемента из 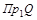 является единственный элемент из является единственный элемент из 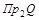 . Следовательно, соответствие является функциональным, функцией. Так как соответствие всюду определено, то имеем полностью определенную функцию, т.е. имеем отображение N1
в N2
. . Следовательно, соответствие является функциональным, функцией. Так как соответствие всюду определено, то имеем полностью определенную функцию, т.е. имеем отображение N1
в N2
.
г) 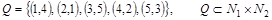 . .
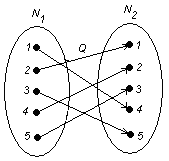
Область определения: 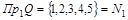 . Значит, соответствие полностью определено. . Значит, соответствие полностью определено.
Область значений: 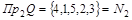 . Значит, соответствие сюръективно. . Значит, соответствие сюръективно.
Образом любого элемента из N1
является единственный элемент из N2
. Следовательно, соответствие является функциональным, функцией.
Так как соответствие всюду определено, сюръективно, функционально и прообразом любого элемента из 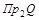 является единственный элемент из является единственный элемент из 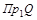 , то соответствие является взаимно однозначным. , то соответствие является взаимно однозначным.
Так как функция полностью определена и соответствие сюръективно, то имеем отображение N1
на N2
.
Так как для любых двух различных элементов из N1
их образы из N2
также различны, то отображение является инъективным.
Так как отображение является одновременно сюръективным и инъективным, то имеем биективное отображение (взаимно однозначное отображение).
Задание 3
Частично упорядоченное множество М задано множеством упорядоченных пар
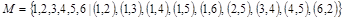 . .
Построить диаграмму и определить, является ли данное множество решеткой. Если заданное множество является решеткой, то определить, является ли решетка дедекиндовой , дистрибутивной.
Решение:
Построим диаграмму:

Построим таблицу:
Пары
элементов
|
Н.Г. |
В.Г. |
Н.Н.Г. |
Н.В.Г. |
| 1,2 |
1 |
2,5 |
1 |
2 |
| 1,3 |
1 |
3,4,5 |
1 |
3 |
| 1,4 |
1 |
4,5 |
1 |
4 |
| 1,5 |
1 |
5 |
1 |
5 |
| 1,6 |
1 |
6,2,5 |
1 |
6 |
| 2,3 |
1 |
5 |
1 |
5 |
| 2,4 |
1 |
5 |
1 |
5 |
| 2,5 |
2,6,1 |
5 |
2 |
5 |
| 2,6 |
6,1 |
2,5 |
6 |
2 |
| 3,4 |
3,1 |
4,5 |
3 |
4 |
| 3,5 |
3,1 |
5 |
3 |
5 |
| 3,6 |
1 |
5 |
1 |
5 |
| 4,5 |
4,3,1 |
5 |
4 |
5 |
| 4,6 |
1 |
5 |
1 |
5 |
| 5,6 |
6,1 |
5 |
6 |
5 |
Так как любая пара элементов имеет единственную наибольшую нижнюю грань и единственную наименьшую верхнюю грань, то заданное частично упорядоченное множество М является решеткой.
Решетка М является дедекиндовой, когда выполняется равенство:
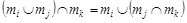
для таких 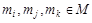 , что , что 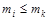 . .
Решетка М не является дедекиндовой, т.к. указанное равенство не вы-полняется, например, для элементов 2, 3, 4:
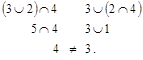
Одним из условий дистрибутивности решетки является ее дедекиндо-вость. Так как решетка М не является дедекиндовой, то она не является дистрибутивной решеткой.
Задание 4
Является ли полной система булевых функций 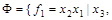 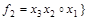 ? Если система функций полная ,то выписать все возможные базисы. ? Если система функций полная ,то выписать все возможные базисы.
Решение:
Рассмотрим функцию 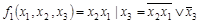 . .
1. Принадлежность функции к классу 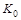 : :
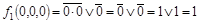 . .
Следовательно, 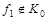 . .
2. Принадлежность функции к классу 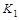 : :
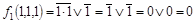 . .
Следовательно, 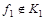 . .
3. Принадлежность функции к классу 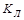 . .
Предположим, что функция линейная и, следовательно, представима в виде полинома Жегалкина первой степени:
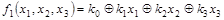 . .
Найдем коэффициенты 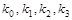 . .
Фиксируем набор 000:
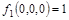 , ,
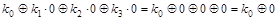 , ,

Следовательно, 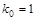 . .
Фиксируем набор 100:
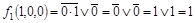 , ,
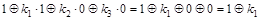 , ,
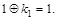
Следовательно, 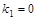 . .
Фиксируем набор 010:
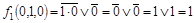 , ,
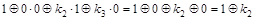 , ,
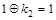 . .
Следовательно, 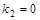 . .
Фиксируем набор 001:
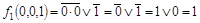 , ,
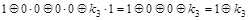 , ,
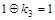 , , 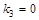 . .
Следовательно, функция (по нашему предположению) может быть представлена полиномом вида:
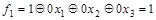 . .
Если функция линейная, то на всех остальных наборах ее значение должно равняться 1. Но на наборе 111 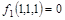 . Значит, функция не является линейной, т.е. . Значит, функция не является линейной, т.е. 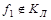 . .
4. Принадлежность функции к классу 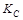 . .
Функция самодвойственная, если на любой паре противоположных наборов (наборов, сумма десятичных эквивалентов которых равна 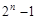 , где п – количество переменных функции) функция принимает противоположные значения. , где п – количество переменных функции) функция принимает противоположные значения.
Вычисляем 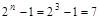 . Вычисляем значения функции на оставшихся наборах: . Вычисляем значения функции на оставшихся наборах:
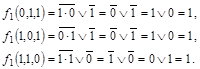 
Строим таблицу:
(000)
0
|
(001)
1
|
(010)
2
|
(011)
3
|
(100)
4
|
(101)
5
|
(110)
6
|
(111)
7
|
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
На наборах 1 и 6, 2 и 5, 3 и 4 функция принимает одинаковые значения. Следовательно, 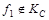 . .
5. Принадлежность функции к классу 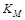 . .
Из таблицы видно: 000 < 111 , но 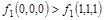 . Следовательно, . Следовательно, 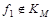 . .
Рассмотрим функцию 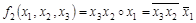 . .
1. Принадлежность функции к классу 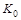 : :
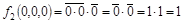 . .
Следовательно, 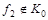 . .
2. Принадлежность функции к классу 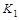 : :
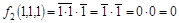 . .
Следовательно, 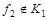 . .
3. Принадлежность функции к классу 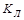 . .
Предполагаем, что
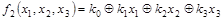 . .
Фиксируем набор 000:
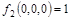 , ,
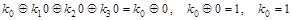 . .
Фиксируем набор 100:
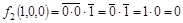 , ,
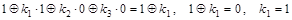 . .
Фиксируем набор 010:
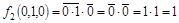 , ,
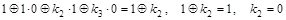 . .
Фиксируем набор 001:
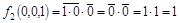 , ,
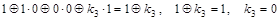 . .
Окончательно получаем
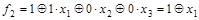 . .
Это равенство не соблюдается на наборе 011:
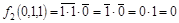 , ,
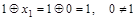 . .
Следовательно, 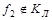 . .
4. Принадлежность функции к классу 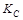 . .
Вычислим значения функции на оставшихся наборах:
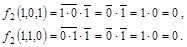
Строим таблицу :
(000)
0
|
(001)
1
|
(010)
2
|
(011)
3
|
(100)
4
|
(101)
5
|
(110)
6
|
(111)
7
|
| 1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
Из таблицы видно, что на наборах 3 и 4 функция принимает одинаковые значения. Следовательно, 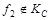 . .
5. Принадлежность функции к классу 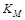 . .
Из таблицы видно, что 111 > 000 , но 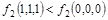 . Следовательно, . Следовательно, 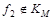 . .
Строим критериальную таблицу:
| К0 |
К1 |
КЛ |
КС |
КМ |
| f1 |
- |
- |
- |
- |
- |
| f2 |
- |
- |
- |
- |
- |
В таблице в каждом столбце стоят минусы. Следовательно, система булевых функций
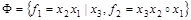
является полной .
Найдем все возможные базисы. По критериальной таблице составим КНФ :
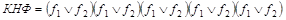 . .
Приведем КНФ к ДНФ :
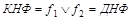 . .
По полученной ДНФ выписываем искомые базисы:
 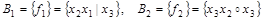 . .
Задание 5
Минимизировать булеву функцию 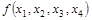 по методу Квайна – Мак-Класки. по методу Квайна – Мак-Класки.
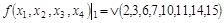
Решение:
1 этап. Определение сокращенной ДНФ.
По десятичным эквивалентам запишем 0-кубы :
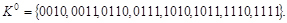
Выполним разбиение на подгруппы:
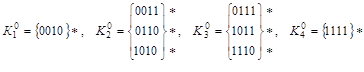 . .
Строим 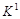 -кубы, сравнивая соседние группы (значок (*) указывает на участие данной импликанты в склеивании): -кубы, сравнивая соседние группы (значок (*) указывает на участие данной импликанты в склеивании):
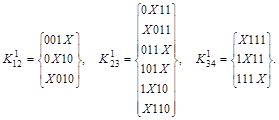
Выполняем разбиение всех 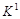 -кубов в зависимости от расположения независимой переменной Х : -кубов в зависимости от расположения независимой переменной Х :
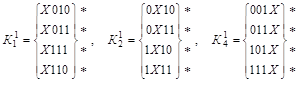 . .
Выполняем сравнение кубов внутри каждой подгруппы с целью построения 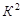 -кубов (значок (*) указывает на участие данной импликанты в склеивании): -кубов (значок (*) указывает на участие данной импликанты в склеивании):
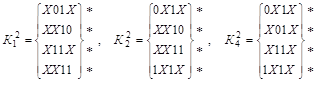 . .
Выполняем сравнение кубов внутри каждой подгруппы с целью построения 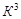 -кубов (значок (*) указывает на участие данной импликанты в склеивании): -кубов (значок (*) указывает на участие данной импликанты в склеивании):
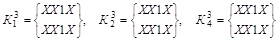 или или
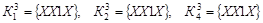 . .
Так как они одинаковы, то 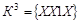 . .
Запишем сокращенную ДНФ, в которую должны быть включены им-пликанта из К 3
и импликанты, не участвовавшие в склеивании (в нашем случае таких импликант нет) :
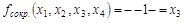 . .
2 этап. Определение тупиковой ДНФ.
Так как все импликанты участвовали в склеивании, и сокращенная ДНФ состоит из одной простой импликанты, то строить таблицу покрытий нет необходимости, т.е.
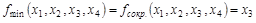 . .
Задание 6
Для неориентированного графа 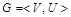 , у которого , у которого 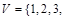 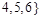 , , 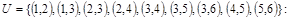
а) вычислить числа 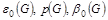 ; ;
б) определить хроматическое число 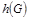 . .
Решение:
Построим граф:

а) Вычислим числа 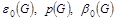 . .
1) 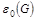 : :
Используя алгоритм выделения пустых подграфов, построим дерево:

Согласно определению 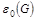 : :
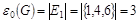 . .
2) 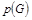 : :
Используя алгоритм выделения полных подграфов, построим дерево:

Здесь 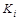 - полные подграфы. Видно, что мощность носителей всех подграфов равна трем, т.е. - полные подграфы. Видно, что мощность носителей всех подграфов равна трем, т.е.
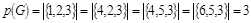 . .
3) 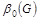 : :

Построим модифицированную матрицу смежности 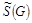 заданного графа G : заданного графа G :
1 2 3 4 5 6
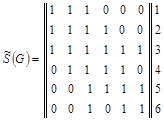  . .
Находим минимальное число строк, покрывающих все столбцы модифи-цированной матрицы . Таких строк – одна. Следовательно,
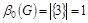 . .
б) Определим хроматическое число 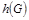 . .

Согласно алгоритму минимальной раскраски вершин графа, выделим все пустые подграфы графа G , т.е. построим дерево (оно построено в пункте а) ):

Построим таблицу:
1 2 3 4 5 6
1. {1,4,6} 1 1 1 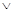
2. {1,5} 1 1
3. {2,5} 1 1 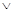
4. {2,6} 1 1
5. {3} 1 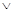
Определяем минимальное число строк, покрывающих все столбцы таблицы. Такими строками могут быть строки 1, 3, 5. Значит,
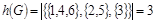 . .
Зададимся красками: для множества вершин 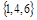 - краска синяя (С ), для множества вершин - краска синяя (С ), для множества вершин 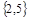 - краска красная ( К ), для множества вершин - краска красная ( К ), для множества вершин 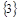 - краска зеленая ( З ). - краска зеленая ( З ).
Раскрасим вершины графа G :

Задание 7
Для заданной сети 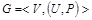 : :
а) найти величину минимального пути и сам путь от вершины 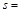 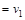 до вершины до вершины 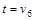 по алгоритму Дейкстры ; по алгоритму Дейкстры ;
б) используя алгоритм Форда-Фалкерсона, определить максимальный поток 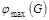 ( v1
– вход , v6
– выход сети ) и указать минимальный разрез, отделяющий v1
от v6
, ( v1
– вход , v6
– выход сети ) и указать минимальный разрез, отделяющий v1
от v6
,
если задана матрица весов (длин, пропускных способностей) Р :
v1
v2
v3
v4
v5
v6
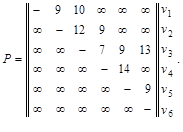
Решение:
Построим сеть:

а) Найдем величину минимального пути и сам путь сети G . Используем для этого алгоритм Дейкстры.
Этап 1. Нахождение длины кратчайшего пути.
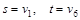 . .
Шаг 1. Полагаем 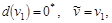
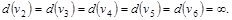
1-я итерация.
Шаг 2. Составим множество вершин, непосредственно следующих за 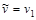 с временными метками: с временными метками: 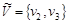 . Пересчитываем временные метки этих вершин: . Пересчитываем временные метки этих вершин: 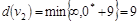 , ,
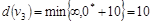 . .
Шаг 3. Одна из временных меток превращается в постоянную:
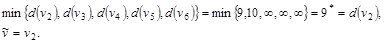
Шаг 4. 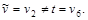 Следовательно, возвращаемся на второй шаг. Следовательно, возвращаемся на второй шаг.
2-я итерация.
Шаг 2.
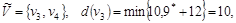
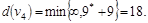
Шаг 3.
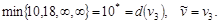
Шаг 4. 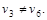 Переход на второй шаг. Переход на второй шаг.
3-я итерация.
Шаг 2.
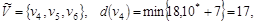
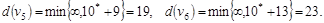
Шаг 3.
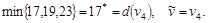
Шаг 4.
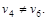 Переход на второй шаг. Переход на второй шаг.
4-я итерация.
Шаг 2.
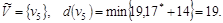
Шаг 3.
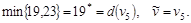
Шаг 4. 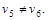 Переход на второй шаг. Переход на второй шаг.
5-я итерация.
Шаг 2.
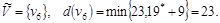
Шаг 3.
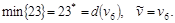
Шаг 4. 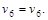 Конец первого этапа. Конец первого этапа.
Следовательно, длина кратчайшего пути равна 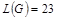 . .
Этап 2. Построение кратчайшего пути.
1-я итерация.
Шаг 5. Составим множество вершин, непосредственно предшествующих 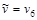 с постоянными метками : с постоянными метками : 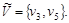 Проверим равенство Проверим равенство
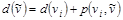
для этих вершин:
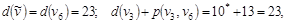 т.е. т.е.
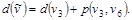
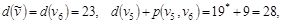 т.е. т.е.
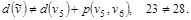
Включаем дугу  в кратчайший путь, в кратчайший путь, 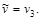
Шаг 6. 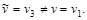 Возвращаемся на пятый шаг. Возвращаемся на пятый шаг.
2-я итерация.
Шаг 5.
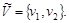
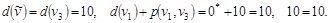
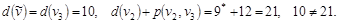
Включаем дугу 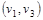 в кратчайший путь, в кратчайший путь, 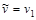 . .
Шаг 6. 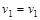 . Завершение второго этапа. . Завершение второго этапа.
Следовательно, кратчайший путь построен. Его образует последовательность дуг: 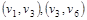 . .
Окончательно, кратчайший путь от вершины 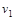 до вершины v6
построен. Его длина (вес) равна до вершины v6
построен. Его длина (вес) равна 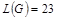 . Сам путь образует последовательность дуг: . Сам путь образует последовательность дуг:
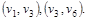
б) Определим максимальный поток 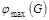 через сеть G. Для этого используем алгоритм Форда-Фалкерсона. через сеть G. Для этого используем алгоритм Форда-Фалкерсона.
 
Выбираем произвольно путь из вершины v1
в вершину v6
. Пусть это будет путь 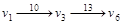 . Минимальную пропускную способность на этом пути, равную 10, имеет дуга . Минимальную пропускную способность на этом пути, равную 10, имеет дуга 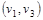 , т.е. , т.е. 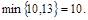 Увеличим на этом пути поток до 10 единиц. Дуга Увеличим на этом пути поток до 10 единиц. Дуга 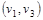 становится насыщенной. Дуга становится насыщенной. Дуга  имеет на данный момент пропускную способность, равную 10. имеет на данный момент пропускную способность, равную 10.
Путь 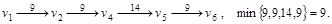 Следовательно, поток на этом пути можно увеличить на 9 единиц. Дуги Следовательно, поток на этом пути можно увеличить на 9 единиц. Дуги  становятся насыщенными. становятся насыщенными.
Других маршрутов нет (другие маршруты проходят через насыщенные дуги). Поток максимален. Делаем разрез вокруг вершины v1
по насыщенным дугам
 
и получаем его величину 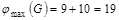 единиц. единиц.
8. Используя алгоритм Краскала, построить остов с наименьшим весом для неориентированного взвешенного графа 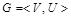 , у которого , у которого 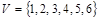 , если заданы веса (длины) ребер: , если заданы веса (длины) ребер:
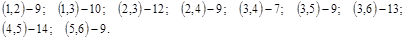
□ Построим граф G :

1. Упорядочим ребра в порядке неубывания веса (длины):
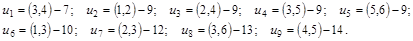

2. Возьмем ребро u1
и поместим его в строящийся остов.
Возьмем ребро u2
и поместим его в строящийся остов (т.к. оно не образует с предыдущим ребром цикла).
Берем ребро u3
и помещаем его в строящийся остов (т.к. оно не образует с предыдущими ребрами цикла).
Берем ребро u4
и помещаем его в строящийся остов (т.к. оно не образует с предыдущими ребрами цикла).
Берем ребро u5
и помещаем его в строящийся остов (т.к. оно не образует цикла с предыдущими ребрами).
Ребра 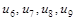 не рассматриваем, т.к. они образуют циклы с предыдущими ребрами. не рассматриваем, т.к. они образуют циклы с предыдущими ребрами.
Проверим окончание алгоритма. Число входящих в остов ребер равно 5. Заданный граф имеет п = 6 вершин и 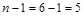 . Таким образом, остов содержит все вершины заданного графа G . . Таким образом, остов содержит все вершины заданного графа G .
Вес (длина) построенного остова

равен 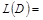 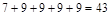 . .
Литература
1. Горбатов В.А. Основы дискретной математики. – М.: Высшая школа, 1986. – 311 с.
2. Коршунов Ю.М. Математические основы кибернетики. – М.: Энерго атомиздат, 1987. – 496 с.
3. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. – М.: Энергоатомиздат, 1988. – 480 с.
4. Шапорев С.Д. Дискретная математика. – СПб.: БХВ-Петербург, 2006. - 400 с.
5. Гаврилов Г.П., Сапоженко А.А. Задачи и упражнения по дискретной математике. – М.: ФИЗМАТЛИТ, 2005. – 416 с.
6. Хаханов В.И., Чумаченко С.В. Дискретная математика ( конспект теоретического материала). – Харьков: ХНУРЭ, 2003. – 246 с.
7. Богданов А.Е. Курс лекций по дискретной математике.–Северодонецк: СТИ, 2006. – 190 с.
|