РЕСПУБЛИКА КАЗАХСТАН
АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра
Автоматической электросвязи
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовой работе
по дисциплине ТЦС
Тема
Проектирование тракта передачи данных между
источником и получателем информации
Выполнила:
М.К. Алибекова
Алматы 2007
Требуется спроектировать среднескоростной тракт передачи данных между двумя источниками и получателями, отстающими друг от друга на L км.
Для повышения верности передачи использовать систему с решающей обратной связью, непрерывной передачей и блокировкой приемника.
Тип кода циклический. Система с РОС работает в режиме обнаружения ошибок с переспросом неправильно принятой информации.
Распределение ошибок в дискретном канале описывается моделью Пуртова Л.П.. Для повышения надежности ТПД применяется постоянное время резервирования.
Требуется:
1) пояснить сущность модели частичного описания дискретного канала (модель Пуртова Л.П.), обратив особое внимание на параметр α - коэффициент группирования ошибок;
2) построить структурную схему системы с РОСнп
и блокировкой и структурную схему алгоритма работы системы;
3) определить оптимальную длину кодовой комбинации n, при которой обеспечивается наибольшая относительная пропускная способность R;
4) определить число проверочных разрядов в кодовой комбинации r, обеспечивающих заданную вероятность необнаружения ошибки. Найти параметры циклического кода n, k, r;
5) выбрать тип образующего полинома g(x) с учетом последней цифры з.к.;
6) построить схему кодера для выбранного g(x) и пояснить его работу;
7) построить схему декодера для выбранного g(x) и пояснить его работу;
8) получить схему кодирующего и декодирующего устройства циклического кода с модуляцией и демодуляцией своего варианта, а также собрать схему с применением пакета «SystemView»;
9) определить объем передаваемой информации Wпри заданном темпе Tпер
и критерии отказа tотк
;
10) определить емкость накопителя М;
11) рассчитать надежностные показатели основного и обходного каналов;
12) по географической карте РК выбрать 2 пункта, отстоящих друг от друга на L км, выбрать магистраль, разбив ее на ряд участков длиной 500-1000 км. Пункты переприема привязать к крупным населенным пунктам;
13) построить временную диаграмму работы системы.
Исходные данные
B= 1200 – скорость модуляции
V= 80000 км/с – скорость распространения информации по каналу связи
Pош
= 0,5 10-3
– вероятность ошибки в дискретном канале
Pно
= 0,8 10-6
- вероятность неопределения кодом ошибки
L= 4700 км – расстояние между источником и получателем
tотк
= 60 сек – критерий отказа
Tпер
= 580 сек – заданный темп
d0
= 6 – минимальное кодовое расстояние
α = 0,7 – коэффициент группирования ошибок
nФМ – тип модуляции
СОДЕРЖАНИЕ
ЗАДАНИЕ
ВВЕДЕНИЕ
ОСНОВНАЯ ЧАСТЬ
1 Модель частичного описания дискретного канала (модель Пуртова Л.П.)
2 Система передачи данных с РОС
2.1 Фазовая манипуляция
3 Оптимальная длина кодовой комбинации при использовании циклического кода в системе с РОС.
4 Параметры циклического кода
5 Расчет надежностных показателей основного и обходного каналов
6 Схемы кодера и декодера циклического кода
6.1 Кодирующее устройство циклического кода
6.2 Декодирующее устройство циклического кода
7 Количество передаваемой информации за время Т
8 Характеристики дискретного канала
8.1 Прямой ДК
8.2 Обратный ДК
9 Временная диаграмма работы системы
10 Магистраль на карте РК
ЗАКЛЮЧЕНИЕ
СПИСОК ЛИТЕРАТУРЫ
ПРИЛОЖЕНИЕ А
ПРИЛОЖЕНИЕ Б
ПРИЛОЖЕНИЕ В
Развитие телекоммуникационных сетей увеличивает роль и значение передачи дискретных сообщений в электросвязи.
Целью дисциплины ТЦС является:
· изложение принципов и методов передачи цифровых сигналов, научных основ и современное состояние технологии цифровой связи;
· дать представление о возможностях и естественных границах реализации цифровых систем передачи и обработки,
· уяснить закономерности, определяющие свойства устройств передачи данных и задачиих функционирования.
Основная задача - обучить теоретическим знаниям и алгоритмам построения систем ТДС, а также привить практические навыки по методологии инженерных расчетов основных характеристик и обучить методам технической эксплуатации цифровых систем и сетей.
Курсовой проект посвящен проектированию тракта передачи данных между источником информации и получателем информации. К качеству тракта передачи данных (ТПД) предъявляются очень высокие требования по верности передачи данных и надежности, поэтому проектируются некоммутируемой ТПД. Для повышения верности передачи использовать систему с решающей обратной связью, непрерывной передачей и блокировкой приемника. Тип кода – циклический.
Решение этих задач раскрывает выполнение основной цели задания – моделирование телекоммуникационных систем.
Кроме того, необходимо собрать схему с применением пакета «SystemView» для моделирования телекоммуникационных систем, кодирующего и декодирующего устройства циклического кода с использованием модуляции и демодуляции.
среднескоростной тракт телекоммуникационная система
По этой модели можно определить зависимость вероятности появления искаженной комбинации от ее длины n и вероятности появления комбинации длиной n с t ошибками.(t<n)
Зависимость вероятности появления искаженной комбинации от ее длины n характеризуется как отношение числа искаженных кодовых комбинаций Nош
(n) общему числу переданных комбинаций N(n):
P(>=1, n) = 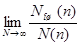 , (1.1) , (1.1)
где вероятность P(>=1, n) – неубывающая функция n.
При n=0, P(>=1, n) = Рош
. При n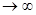 , P(>=1, n) , P(>=1, n) 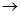 1 1
P(>=1, n)=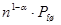 , (1.2) , (1.2)
где α – показатель группирования ошибок
α = 0 – пакетирование ошибок отсутствует, и появление ошибок следует считать независимым.
α = 0,5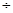 0,7 – наблюдается на кабельных линиях связи, т.к. кратковременные прерывания приводят к появлению групп с большой плотностью ошибок. 0,7 – наблюдается на кабельных линиях связи, т.к. кратковременные прерывания приводят к появлению групп с большой плотностью ошибок.
α = 0,3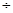 0,5 – пакетирование в радиорелейных линиях связи с интервалами большой плотности ошибок; имеется интервалы с редкими ошибками. 0,5 – пакетирование в радиорелейных линиях связи с интервалами большой плотности ошибок; имеется интервалы с редкими ошибками.
α = 0,3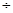 0,4 – в радиотелеграфных каналах. 0,4 – в радиотелеграфных каналах.
Распределение ошибок в комбинациях различной длины оценивает не только вероятность появления искаженных комбинаций (хотя бы 1 ошибка), но и вероятность комбинаций длиной n и t наперед заданными ошибками P(>= t, n):
P(>= t, n)= (1.3) (1.3)
Группирование ошибок приводит к увеличению числа кодовых комбинаций, пораженных ошибками большой кратности.
При группировании ошибок уменьшается число искаженных кодовых комбинаций заданной длины n.
Примеры зависимости 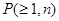 от длины блока n показаны на рисунке 1. от длины блока n показаны на рисунке 1.

Рисунок 1
- Вероятности ошибки 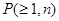 в зависимости от длины n: 1 – КВ радиотелеграфный канал; 2 – коммутируемый канал ТЧ кабельной линии; 3 – канал ТЧ радиорелейной линии; 4 – телеграфный канал кабельной линии; 5 – некоммутируемый канал ТЧ кабельной линии. в зависимости от длины n: 1 – КВ радиотелеграфный канал; 2 – коммутируемый канал ТЧ кабельной линии; 3 – канал ТЧ радиорелейной линии; 4 – телеграфный канал кабельной линии; 5 – некоммутируемый канал ТЧ кабельной линии.
Эти зависимости, снятые в реальных каналах связи и отмеченные на рисунке 1 точками, хорошо аппроксимируются прямыми линиями при логарифмических масштабах. Для определенной вероятности ошибок (Pош
=0,002) пунктиром показаны две зависимости. Если бы ошибки не зависели друг от друга, то вероятность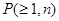 не зависела бы от n и шла под углом 45˚. Если бы ошибки были сгруппированы подряд в одну группу, то не зависела бы от n и шла под углом 45˚. Если бы ошибки были сгруппированы подряд в одну группу, то 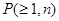 не зависела бы от длины кодовой комбинации n и была бы параллельна оси абсцисс. Из рисунка 1 видно, что характеристика реального канала (прямая 2) лежит между этими двумя предельными характеристиками.
не зависела бы от длины кодовой комбинации n и была бы параллельна оси абсцисс. Из рисунка 1 видно, что характеристика реального канала (прямая 2) лежит между этими двумя предельными характеристиками.

Рисунок 2
– Структурная схема системы с РОСнп
и блокировкой
На рисунке 2 представлена структурная схема системы с РОСнп
и блокировкой. Здесь:
ИИ
– источник информации;
КУ
– кодирующее устройство;
ДК
– прямой дискретный канал;
РУ
– решающее устройство;
ДКУ
– декодирующее устройство;
УУ
– устройство управления;
УДС
– устройство декодирования сигнала;
УФС
– устройство формирования сигнала;
ПИ
– получатель информации
Передача информации осуществляется следующим образом. При поступлении от источника информации ИИ кодовой комбинации происходят ее кодирование помехоустойчивым кодом (в КУ) и запись в накопитель передачи 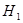 . Закодированная информация передается по прямому дискретному каналу. . Закодированная информация передается по прямому дискретному каналу.
Принятая из прямого дискретного канала (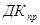 ) кодовая комбинация кодируется (в ДКУ) и записывается в накопитель приема ) кодовая комбинация кодируется (в ДКУ) и записывается в накопитель приема 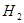 . Комбинация может быть декодирована правильно, то есть соответствовать переданной кодовой комбинации; она может содержать необнаруженную ошибку в результате перехода переданной кодовой комбинации в другую разрешенную кодовую комбинацию; наконец, в результате декодирования может быть обнаружена ошибка (если переданная кодовая комбинация перешла в неразрешенную). Вероятность наступления каждого из трех указанных событий зависит от характеристик дискретного канала, помехоустойчивого кода и метода декодирования. . Комбинация может быть декодирована правильно, то есть соответствовать переданной кодовой комбинации; она может содержать необнаруженную ошибку в результате перехода переданной кодовой комбинации в другую разрешенную кодовую комбинацию; наконец, в результате декодирования может быть обнаружена ошибка (если переданная кодовая комбинация перешла в неразрешенную). Вероятность наступления каждого из трех указанных событий зависит от характеристик дискретного канала, помехоустойчивого кода и метода декодирования.
В зависимости от результатов декодирования решающее устройство РУ принимает решение о выдаче кодовой комбинации из накопителя приема через схему 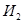 потребителю или о ее стирании в накопителе. Первое из этих решений принимается в случае отсутствия ошибок или при необнаруженных ошибках, а второе – при обнаружении ошибок. В первом случае одновременно с выдачей кодовой комбинации получателю информации ПИ устройством управления потребителю или о ее стирании в накопителе. Первое из этих решений принимается в случае отсутствия ошибок или при необнаруженных ошибках, а второе – при обнаружении ошибок. В первом случае одновременно с выдачей кодовой комбинации получателю информации ПИ устройством управления 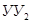 и устройством УФС формирования сигнала ОС формируется сигнал подтверждения, который по обратному дискретному каналу ( и устройством УФС формирования сигнала ОС формируется сигнал подтверждения, который по обратному дискретному каналу (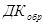 ) передается в передатчик. После получения сигнала подтверждения и его декодировании в УДС, ) передается в передатчик. После получения сигнала подтверждения и его декодировании в УДС, 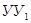 передатчика запрашивает у источника информации следующую кодовую комбинацию и описанный выше цикл работы повторяется. Схема передатчика запрашивает у источника информации следующую кодовую комбинацию и описанный выше цикл работы повторяется. Схема 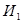 при этом закрыта, поэтому при поступлении новой кодовой комбинации ранее переданная комбинация в накопителе передачи стирается. Во втором случае одновременно с решением о стирании в УФС формируется сигнал переспроса, который по обратному дискретному каналу передается в передатчик. После получения и декодирования сигнала переспроса из накопителя передачи через схему ИЛИ повторно передается та же кодовая комбинация. при этом закрыта, поэтому при поступлении новой кодовой комбинации ранее переданная комбинация в накопителе передачи стирается. Во втором случае одновременно с решением о стирании в УФС формируется сигнал переспроса, который по обратному дискретному каналу передается в передатчик. После получения и декодирования сигнала переспроса из накопителя передачи через схему ИЛИ повторно передается та же кодовая комбинация.
Блоки управления приемником и передатчиком работают согласно структурной схеме алгоритма, представленной на рисунке 3.

Рисунок 3
– Структурная схема алгоритма системы с РОСнп
и блокировкой
2.1 Фазовая манипуляция
Фазовая манипуляция (phaseshiftkeying - PSK) была разработана в начале развития программы исследования дальнего космоса; сейчас схема PSK широко используется в коммерческих и военных системах связи. Фазо-манипулированный сигнал имеет следующий вид:
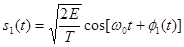 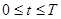 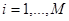
Здесь фазовый член 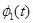 может принимать М дискретных значений, обычно определяемых следующим образом: может принимать М дискретных значений, обычно определяемых следующим образом:
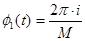 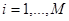
Аналитическое представление:Сигнал: Вектор:

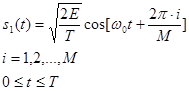
Параметр Е – это энергия символа, Т – время передачи символа, 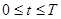 . Работа схемы модуляции заключается в смещении фазы модулируемого сигнала s1
(t) на одно из двух значений, нуль или π (180º). Типичный вид BPSK-модулированного сигнала приведен на рис., где явно видны характерные резкие изменения фазы при переходе между символами; если модулируемый поток данных состоит из чередующихся нулей и единиц, такие резкие изменения будут происходить при каждом переходе. Модулированный сигнал можно представить как вектор на графике в полярной системе координат; длина вектора соответствует амплитуде сигнала, а его ориентация в общем М-арном случае – фаза сигнала относительно других М-1 сигналов набора. При модуляции BPSK векторное представление дает два противофазных(180º) вектора. Наборы сигналов, которые могут быть представлены подобными противофазными векторами, называются антиподными. . Работа схемы модуляции заключается в смещении фазы модулируемого сигнала s1
(t) на одно из двух значений, нуль или π (180º). Типичный вид BPSK-модулированного сигнала приведен на рис., где явно видны характерные резкие изменения фазы при переходе между символами; если модулируемый поток данных состоит из чередующихся нулей и единиц, такие резкие изменения будут происходить при каждом переходе. Модулированный сигнал можно представить как вектор на графике в полярной системе координат; длина вектора соответствует амплитуде сигнала, а его ориентация в общем М-арном случае – фаза сигнала относительно других М-1 сигналов набора. При модуляции BPSK векторное представление дает два противофазных(180º) вектора. Наборы сигналов, которые могут быть представлены подобными противофазными векторами, называются антиподными.
На практике фазовая манипуляция используется при небольшом числе возможных значений начальной фазы – как правило, 2, 4 или 8. Кроме того, при приеме сигнала сложно измерить абсолютное значение начальной фазы; значительно проще определить относительный фазовый сдвиг между двумя соседними символами. Поэтому обычно используется фазоразностная манипуляция (синонимы – дифференциальная фазовая манипуляция, относительная фазовая манипуляция; английский термин - differentialphaseshiftkeying , DPSK).
3
О
птимальная длина кодовой комбинации при использовании циклического кода в системе с РОС
Длина кодовой комбинации n должна быть выбрана таким образом, чтобы обеспечить наибольшую пропускную способность канала связи. При использовании корректирующего кода кодовая комбинация содержит n разрядов, из которых k разрядов являются информационными, а r разрядов – проверочными:
n= k+r (3.1)
Если в системе связи используются двоичные сигналы (сигналы типа «1» и «0») и каждый единичный элемент несет не более одного бита информации, то между скоростью передачи информации и скоростью модуляции существует соотношение
C = (k/n)*B, (3.2)
где С – скорость передачи информации, бит/с;
В – скорость модуляции, Бод.
Очевидно, что тем меньше r, тем больше отношение k/n приближается к 1, тем меньше отличается С и В, т.е. тем выше пропускная способность системы связи.
Известно также [3, стр. 104], что для циклических кодов с минимальным кодовым расстоянием d0
=3 справедливо соотношение
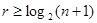 (3.3) (3.3)
Видно, что чем больше n, тем ближе отношение k/n к 1. Так, например, при n = 7, r=3, k=4, k/n = 0,571; при n = 255, r=8, k=247, k/n = 0,964; n = 1023, r=10, k=1013, k/n = 0,990.
Приведенное утверждение справедливо для больших d0
, хотя точных соотношений для связей между r и n нет. Существуют только верхние и нижние оценки, указанные на стр. 104 [3].
Из изложенного можно сделать вывод, что с точки зрения внесения постоянной избыточности в кодовую комбинацию выгодно выбирать длинные кодовые комбинации, так как с увеличением n относительная пропускная способность увеличивается, стремясь к пределу, равному 1.
R= C/B= k/n (3.4)
В реальных каналах связи действуют помехи, приводящие к появлению ошибок в кодовых комбинациях. При обнаружении ошибки декодирующим устройством в системах с РОС производится переспрос группы кодовых комбинаций. Во время переспроса полезная информации уменьшается.
Можно показать, что в этом случае
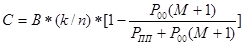 , (3.5) , (3.5)
где Р00
– вероятность обнаружения ошибки декодером (вероятность переспроса);
РПП
– вероятность правильного приема (безошибочного приема) кодовой комбинации;
М – емкость накопителя передатчика в числе кодовых комбинаций.
При малых вероятностях ошибки в канале связи (Рош.
< 10-3
) вероятность Р00
также мала, поэтому знаменатель мало отличается от 1 и можно считать
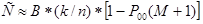 (3.6) (3.6)
При независимых ошибках в канале связи, при 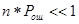
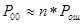 , ,
тогда
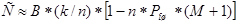 (3.7) (3.7)
Емкость накопителя [2, стр. 323]
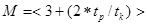 , (3.8) , (3.8)
где tp
– время распространения сигнала по каналу связи, с;
tk
– длительность кодовой комбинации из n разрядов, с.
Знак < > - означает, что при расчете М следует брать большее ближайшее целое значение. Но
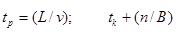 , (3.9) , (3.9)
где L – расстояние между оконечными станциями, км;
v – скорость распространения сигнала по каналу связи, км/с;
B – скорость модуляции, Бод.
После простейших подстановок окончательно имеем
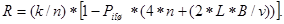 (3.10) (3.10)
Нетрудно заметить, что при Рош
= 0 формула (3.10) превращается в формулу (3.4).
При наличии ошибок в канале связи величина R является функцией Pош
, n, k, B, L, v. Следовательно, существует оптимальное n (при заданных Pош
, B, L, v), при котором относительная пропускная способность будет максимальной.
Формула (3.10) еще более усложняется в случае зависимых ошибок в канале связи (при пакетировании ошибок).
Выведем эту формулу для модели ошибок Пуртова.
Как показано в [1], число ошибок tоб
в комбинации, длинной в n разрядов, определяется формулой 7.38 [1]. Для обнаружения такого числа ошибок находим циклический код с кодовым расстоянием d0
не менее 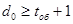 . Поэтому, согласно формуле 7.38 [1], необходимо определить вероятность . Поэтому, согласно формуле 7.38 [1], необходимо определить вероятность
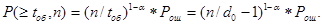
Как показано [4], с некоторым приближением можно связать вероятность 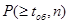 с вероятностью не обнаружения декодером ошибки РНО
и числом проверочных разрядов в кодовой комбинации с вероятностью не обнаружения декодером ошибки РНО
и числом проверочных разрядов в кодовой комбинации
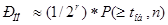 (3.11) (3.11)
Подставляя значение 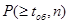 в (9) с заменой tоб
на d0
-1, имеем в (9) с заменой tоб
на d0
-1, имеем
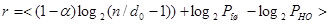 (3.12) (3.12)
При расчетах на микрокалькуляторах удобнее пользоваться десятичными логарифмами.
После преобразований
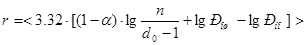 (3.13) (3.13)
Возвращаясь к формулам (3.7) и (3.10) и производя замену k на n-r с учетом значения r, из формулы (3.13) получим
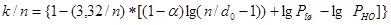
Второй член формулы (3.10) с учетом группирования ошибок по соотношению 7.37 [1] примет вид
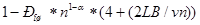
Окончательно
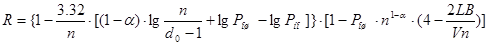 (3.14) (3.14)
Примем n равной 31. Если при расчете пропускная способность R будет меньше 0.6, то рассчитаем ее для n равной 63.
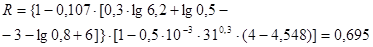
Итак, в моем случае:
n = 31
R = 0.695
4. П
араметры циклического кода
К параметром циклического кода относятся:
n
– длина кодовой комбинации (разрядов);
k
– длина информационной части кодовой комбинации (разрядов);
r
– длина проверочной части кодовой комбинации (разрядов);
g
(
x
)
– вид образующего полинома циклического кода.
После определения оптимальной длины кодовой комбинации n, обеспечивающей наибольшую относительную пропускную способность R, по формуле (3.13) определяют число проверочных разрядов:
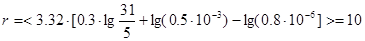
Так как n , в моем случае, равно 31, то воспользовавшись формулой (3.1), определим число информационных символов k:
k = 31 – 10 = 21
Выбираем образующий полином согласно последней цифре зачетной книжки и числу проверочных символов, которые определяют степень g(x):
g (x) = х10
+х4
+х3
+х+1
5.
Расчет надежностных показателей основного и обходного каналов
Вероятность появления ошибки известна (Рош
=0,5∙10-3
), полная вероятность будет складываться из суммы следующих составляющих рпр
– правильный прием, рно
– необнаружения ошибки, роб
– вероятность обнаружения ошибки декодером (вероятность переспроса).
Зависимость вероятности появления искаженной комбинации от ее длины характеризуется как отношение числа искаженных кодовых комбинаций Nош
(n) к общему числу переданных комбинаций N(n):
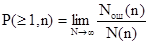 (5.1) (5.1)
Вероятность Р(≥1,n) является не убывающей функцией n. При n=1 Р(≥1,n)=рош
, а при n→∞ вероятность Р(≥1,n) →1.
Вероятность необнаруживаемой кодом ошибки определяется по формуле:
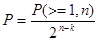 (5.2) (5.2)
В моем случае она равна 1,368*10-6
.
Вероятность обнаруживаемой кодом ошибки:
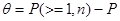 (5.3) (5.3)
Подставив числовые значения, получим 1,4*10-3
.
Вероятность правильного прием:
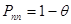 (5.4) (5.4)
В данном случае она равна 0,999,то есть близка к единице.
Избыточность кода:
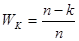 (5.5) (5.5)
Подставим параметры циклического кода и получим 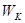 =0,323. =0,323.
Скорость кода:
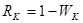 (5.6) (5.6)
Подставим в данную формулу вычисленное ранее значение избыточности кода и получим скорость кода равную 0,667.
Избыточность необходимая для обеспечения в ДК вероятности необнаружения кодом ошибки определяется по формуле:
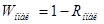 , (5.7) , (5.7)
где Rнпбл
– средняя относительная скорость передачи в РОСнп
и блокировкой
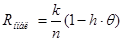 (5.8) (5.8)
где 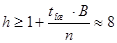
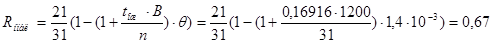
Итак, избыточность необходимая для обеспечения в ДК вероятности необнаружения кодом ошибки будет равна 0,33.
6. С
хемы кодера и декодера циклического кода
Рассмотрим построение и принцип действия кодера и декодера циклического (31,21) кода. Выбираем образующий:
g (x) = х10
+х4
+х3
+х+1
6.1 Кодирующее устройство циклического кода
Работа кодера на его выходе характеризуется следующим:
1.Формирование k
элементов информационной группы и одновременно деление полинома, отображающего информационную часть х
r
m
(х),
на порождающий (образующий ) полином g
(
х)
с целью получения остатка от деления r
(х)
.
2. Формирование проверочных r
элементов путем считывания их с ячеек схемы деления х
r
m
(
х)
на выход кодера.
Структурная схема кодера приведена на рисунке 4.
Цикл работы кодера для передачи n = 31
единичных элементов составляет n
тактов. Тактовые сигналы формируются передающим распределителем, которыйна схеме не указан .
Первый режим работы кодера длится k
= 21
тактов. От первого тактового импульса триггер Т занимает положение, при котором на его прямом выходе появляется сигнал "1", а на инверсном - сигнал "0". Сигналом "1" открываются ключи (логические схемы И) 1 и 3 . Сигналом "0" ключ 2закрыт.В таком состоянии триггер и ключи находятся k+1
тактов, т.е. 22 тактов.За это времяна выход кодера через открытый ключ 1 поступят 56 единичных элементов информационной группы k =21
.
Одновременно через открытый ключ 3 информационные элементы поступаютна устройство деления многочлена х
r
m
(
х)
наg
(
х).
Деление осуществляется многотактным фильтром с числом ячеек, равным числу проверочных разрядов (степени порождающего полинома). В рассматриваемом случае число ячеек г=10
. Число сумматоров в устройстве равно числу ненулевых членов g(
х)
минус единица.
В нашем случае число сумматоров равно четырем. Сумматоры устанавливаются после ячеек, соответствующих ненулевым членам g
(х)
. Поскольку все неприводимые полиномы имеют член х°=1,
то соответствующий этому члену сумматор установлен перед ключом 3 (логической схемой И).
После k=21 тактов в ячейках устройства деления окажется записанным остаток от деления г(х)
.
При воздействии k
+1
= 22 тактового импульса триггер Т изменяет свое состояние: на инверсном выходе появляется сигнал "1", а на прямом - "0". Ключи 1 и 3 закрываются, а ключ 2 открывается. За оставшиеся r
=10
тактов элементы остатка от деления (проверочная группа) через ключ 2 поступают на выход кодера, также начиная со старшего разряда.

Рисунок 4
- Структурная схема кодера

Рисунок 5
- Структурная схема декодера
6.2 Декодирующее устройство циклического кода
Функционирование схемы декодера (рисунок 5) сводится к следующему. Принятая кодовая комбинация, которая отображается полиномом Р(х)
поступает в декодирующий регистр и одновременно в ячейки буферного регистра, который содержит k
ячеек. Ячейки буферного регистра связаны через логические схемы "нет", пропускающие сигналы только при наличии "1" на первом входе и "0" - на втором (этот вход отмечен кружочком). На вход буферного регистра кодовая комбинация поступит через схему И1
. Этот ключ открывается с выхода триггера Т первым тактовым импульсом и закрывается k+1
тактовым импульсом (полностью аналогично работе триггера Т в схеме кодера) . Таким образом, после k
тактов информационная группа элементов будет записана в буферный регистр. Схемы НЕТ в режиме заполнения регистра открыты, ибо на вторые входы напряжение со стороны ключа И2
не поступает.
Одновременно в декодирующем регистре происходит в продолжение всехn
=31
тактов деление кодовой комбинации (полином Р(х)
на порождающий полином g
(
х)
). Схема декодирующего регистра полностью аналогична схеме деления кодера, которая подробно рассматривалась выше. Если в результате деления получится нулевой остаток -
синдром S
(х)
=
0, топоследующие тактовыеимпульсы спишут информационные элементы на выход декодера.
При наличии ошибок в принятой комбинациисиндром S(х)
не равен 0. Это означает, что после n
-
го(31) такта хотя бы водной ячейкедекодирующего регистра будетзаписана “
1”. Тогдана выходе схемы ИЛИ появится сигнал. Ключ2 (схема И2
) сработает, схемы НЕТ буферного регистра закроются, а очереднойтактовый импульс переведет все ячейки регистра в состояние "0". Неправильно принятаяинформация будетстерта. Одновременно сигнал стиранияиспользуется как команданаблокировку приемника и переспрос.
7.
Количество передаваемой информации за время Т
Пусть требуется передавать информацию за временной интервал Т который называется темпом передачи информации Критерий отказа tотк
-
это суммарная длительность всех неисправностей,
которая допустима за время Т. Если время неисправностей за промежуток времени Т превысит tотк
, то система передачи данных будет находиться в состоянии отказа,
С учетом выбранных параметров кода
W = R*B*(Tпер
– tотк
), (7.1)
где R - наибольшая относительная пропускная способность для выбранных параметров циклического кода.
W = 0,695∙1200∙(580-60)=433680 бит
8.1 Прямой ДК
Максимальная скорость работы по каналу равна скорости модуляции В = 1200 Бод. Распределение вероятности возникновения хотя бы одной ошибки на длине n определяется по формуле (1.2)
P(>=1, n) = 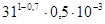 = 1,401*10-3 = 1,401*10-3
Распределение вероятности возникновения ошибки кратности t и более на длине n определяется по формуле (1.3) для
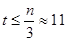
она равна
P(>= t, n) = 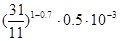 = 6,823*10-4 = 6,823*10-4
для
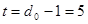
P(>= t, n) =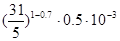 = 8,643*10-4 = 8,643*10-4
Время распределения определим по формуле (3.9):
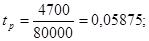
Максимальная скорость работы по каналу равна скорости модуляции В = 200 Бод. Распределение вероятности возникновения хотя бы одной ошибки на длине n и распределение вероятности возникновения ошибки кратности t и более на длине n такие как в прямом ДК.
9. В
ре
менная диаграмма работы системы
Емкость накопителя М определяется по формуле (3.8)
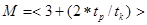 = 8, = 8,
где tp
– время распространения сигнала по каналу связи, с;
tk
– длительность кодовой комбинации из n разрядов, с.
Время распространения сигнала по каналу связи и длительность кодовой комбинации из n разрядов определим по формулам (3.9):
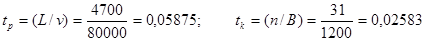 , ,
где L – расстояние между оконечными станциями, км;
v – скорость распространения сигнала по каналу связи, км/с;
B – скорость модуляции, Бод.
Будем считать, что
tс
= tк
= 0,02583 сек
tа.к.
= tа.с.
= 0.5 tк
= 0,012915 сек
Для правильного построения диаграммы совершенно необходимо соблюдать временной масштаб и учитывать соотношение между величинами tс
, tк
, tа.к.
, tа.с.
, tр
.
tож
= tp'
+ tр’’
+ tак
+ tас
+ tc
, (8.1)
где tp'
– время распределения по прямому ДК
tр’’
- время распределения по обратному ДК
tак
– время анализа канала
tас
- время анализа сигнала
Таким образом,
tож
=2*0,05875+2*0,012915+0,02583= 0,16916 сек
Временная диаграмма (рисунок 6) иллюстрирует работу системы с РОСНП
и блокировкой при обнаружении ошибки во второй комбинации в случае с h=8. Как видно из диаграммы, передача комбинации ИИ осуществляется непрерывно до момента получения передатчиком сигнала переспроса. После этого передача информации от ИИ прекращается на время tож
и 8 комбинаций начиная со второй. В это время в приемнике стираются h комбинаций: вторая комбинация, в которой обнаружена ошибка (отмечена звездочкой) и 6 последующих комбинаций (заштрихованы). Получив переданные из накопителя комбинации (от второй до 8-ой включительно) приемник выдает их ПИ, а передатчик продолжает передачу последующих комбинаций.

Рисунок 6
– Временная диаграмма работы системы
Уральск - 0 км;
Актюбинск - 1004,5 км;
Кызылорда - 1893,5 км;
Шымкент – 2100 км;
Тараз - 2453,5 км;
Алматы - 3500,5 км;
Караганда – 4020,5 км;
Астана - 4700 км.

Рисунок 7
– Выбор магистрали по карте РК
ЗАКЛЮЧЕНИЕ
В ходе выполнения данной курсовой работы я
· пояснила сущность модели частичного описания дискретного канала (модель Пуртова Л.П.);
· построила структурную схему системы с РОСнп
и блокировкой и структурную схему алгоритма работы системы;
· определила оптимальную длину кодовой комбинации n, при которой обеспечивается наибольшая относительная пропускная способность R, а также число проверочных разрядов в кодовой комбинации r, обеспечивающих заданную вероятность необнаружения ошибки;
· нашла параметры циклического кода n, k, r;
· выбрала тип образующего полинома g(x) с учетом последней цифры з.к.;
· построила схему кодера и декодера для выбранного g(x) и пояснила их работу;
· получила схему кодирующего и декодирующего устройства циклического кода своего варианта, а также собрала схему с применением пакета «SystemView»;
· определила объем передаваемой информации W при заданном темпе Tпер
и критерии отказа tотк,
емкость накопителя М;
· рассчитала надежностные показатели основного и обходного каналов;
· построила временную диаграмму работы системы.
В результате мной была выполнена основная задача курсовой работы – моделирование телекоммуникационных систем.
СПИСОК ЛИТЕРАТУРЫ
1. Скляр Б. Цифровая связь. Теоретические основы и практическое применение: 2-е изд. /Пер. с англ.- М.: Издательский дом «Вильямс», 2003. - 1104 с.
2. Прокис Дж. Цифровая связь. Радио и связь, 2000.-797с.
3. А.Б. Сергиенко. Цифровая обработка сигналов: Учебник для вузов. - М.:-2002.
4. Фирменный стандарт. Работы учебные. Общие требования к построению, изложению, оформлению и содержанию. ФС РК 10352-1910-У-е-001-2002. – Алматы: АИЭС, 2002.
5. 1 Шварцман В.О., Емельянов Г.А. Теория передачи дискретной информации. – М.: Связь, 1979. -424 с.
6. Передача дискретных сообщений / Под ред. В.П. Шувалова. - М.: Радио и связь, 1990. -464 с.
7. Емельянов Г.А., Шварцман В.О. Передача дискретной информации. - М.: Радио и связь, 1982. - 240 с.
8. Пуртов Л.П. и др. Элементы теории передачи дискретной информации. – М.: Связь, 1972. – 232 с.
9. Колесник В.Д., Мирончиков Е.Т.. Декодирование циклических кодов.- М.: Связь, 1968.
Кодер циклического кода

Рисунок А.1 –
Схема кодера циклического кода, выполненная с применением пакета «SystemView»

Рисунок А.2 –
Входные и выходные сигналы кодера циклического кода
Декодер циклического кода

Рисунок Б.1 –
Схема декодера циклического кода, выполненная с применением пакета «SystemView»

Рисунок Б.2 –
Входные и выходные сигналы декодера циклического кода

Рисунок В.1 –
Входные и выходные последовательности для кодера и декодера циклического кода
Размещено на http://www.
|