Белгородский государственный университет
Факультет компьютерных наук и телекоммуникаций
Кафедра математических методов и информационных технологий
В экономике и управлении
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА К КУРСОВОЙ РАБОТЕ
По дисциплине: “Основы теории цепей”
на тему: “Анализ переходных процессов в электрических цепях”
Содержание
Введение
1. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
1.1 Общие сведения
1.2 Классический метод расчета
1.3
Операторный метод расчета
2.РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
2.1 Определение начальных и конечных условий в цепях с ненулевыми начальными условиями
2.2 Определение переходных процессов классическим методом
2.3 Построение графиков
2.4 Расчет графиков переходного процесса
2.5 Обобщенные характеристики цепи
Заключение
Список использованных источников
Введение
Нестационарные явления играют важную роль в работе многих устройств, применяемых в современной радиотехнике и электронике. Инженеру по направлению «Телекоммуникация» в своей повседневной деятельности приходится постоянно соприкасаться с переходными процессами и прохождением сигналов через линейные электрические цепи. Данная курсовая работа посвящена изучению переходных процессов.
Основной целью работы является приобретение навыков использования теоретических знаний на практике, при расчете переходных процессов, происходящих в линейных электрических цепях.
Пояснительная записка содержит теоретическую информацию, необходимую для анализа переходных процессов. Среди всех существующих методов расчета переходных процессов наибольшее внимание в данной записке уделено операторному методу анализа. В практической части приводится конкретный пример анализа переходных процессов операторным методом, основанный на теоретических знаниях.
В результате чего произведено более глубокое и эффективное изучение материала по теме: «Анализ переходных процессов в электрических цепях», а также освоение новых программ и приложений, требуемых при построении схем, графиков и расчёте формул.
1.1 Общие сведения
Переходные процессы возникают в электрических цепях при различных воздействиях, приводящих к изменению их режима работы, т.е. при действии различного рода коммутационной аппаратуры, например ключей, переключателей для включения или отключения источника или приёмника энергии, при обрывах цепи, при коротких замыканиях отдельных участков цепи и т.д.
Физической причиной возникновения переходных процессов в цепях является наличие в них катушек индуктивности и конденсаторов, т.е. индуктивных и емкостных элементов в соответствующих схемах замещения. Объясняется это тем, что энергия магнитного и электрического полей этих элементов не может измениться скачком при коммутации в цепи.
Переходный процесс в цепи описывается дифференциальным уравнением - неоднородным или однородным, если её схема замещения содержит или не содержит источники ЭДС и тока. Переходный процесс в линейной цепи описывается линейными дифференциальными уравнениями, а в нелинейной – нелинейными.
Для решения линейных дифференциальных уравнений с постоянными параметрами разработаны различные аналитические методы: классический, оперативный, метод интеграла Фурье и другие, которые применяются и для расчета переходных процессов. Наиболее распространенными я являются классический и оперативный методы. Первый обладает физической наглядностью и удобен для расчёта простых цепей, а второй упрощает расчёт сложных цепей.
1.2
Классический метод
Название метода «классический» отражает использование в нем решений дифференциальных уравнений с постоянными параметрами методами классической математики. Классический метод основан на составлении системы дифференциальных уравнений, которым должны удовлетворять напряжения и токи в цепи, рассматриваемые как неизвестные функции времени, с последующим нахождением ее общего решения и на последнем этапе определением таких значений постоянных общего решения, которые удовлетворяют начальным условиям каждой конкретной задачи.
Для расчета переходных процессов классическим методом необходимо составить систему уравнений на основе законов Кирхгофа, Ома, электромагнитной индукции и т.д., описывающих состояние цепи после коммутации, и исключением переменных получить одно дифференциальное уравнение, в общем случае неоднородное относительно искомого тока или напряжения.
Если для классического метода анализа колебаний в линейных электрических цепях с сосредоточенными элементами при произвольных воздействиях сводится к решению неоднородной системы обыкновенных линейных дифференциальных уравнений при заданных начальных условиях, то для аналитического решения этих уравнений в теории электрических цепей нашли широкое применение операторные методы. Операторный метод анализа позволяет сводить линейные дифференциальные уравнения к более простым алгебраическим уравнениям что в ряде случаев упрощает расчеты. Его идея заключается в том, что расчет переходного процесса переносится из области функций действительной переменной (времени t) в область функций комплексной переменной р. Такое преобразование называется прямым.
В настоящее время операторные методы связывают с применением преобразования Лапласа:
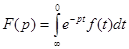 , ,
где f(t) – однозначная функция времени, называемая оригиналом; F(p) – функция комплексной переменной р, называемая лапласовым изображением.
2. РАССЧЁТ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
2.1 Определение начальных и конечных условий в цепях с нулевыми начальными условиями
В приведенной схеме (рисунок 2.1) определить начальные и конечные условия для всех токов и напряжений в цепи с нулевыми начальными условиями. Результаты вычислений внести в таблицу.
Данные для рассчета приведены в таблице 2.1:
Таблица 2.1
| R1
, Ом |
R2
, Ом |
С, Ф |
С1
, Ф |
L, Гн |
L1
, Гн |
Е, В |
| 4 |
12 |
1/12 |
- |
6/5 |
- |
8 |

Рис. 2.1 Схема индивидуального варианта.
Решение.
2.1.1 Начальные условия 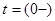
Переходной процесс в схеме начинается в момент включения ключа К. До этого момента времени все токи и напряжения равны нулю.
2.1.2 Расчёт начальных условий 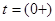 . .
Изобразим эквивалентную схему цепи для времени 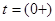 . Так как это цепь с нулевыми начальными условиями, то индуктивность . Так как это цепь с нулевыми начальными условиями, то индуктивность 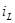 заменим разрывом, а емкость – перемычкой (рисунок 2.2). заменим разрывом, а емкость – перемычкой (рисунок 2.2).

Рис. 2.2 Эквивалентная схема цепи для времени 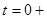 . .
В этой схеме
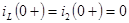 ; ;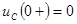 . .
Тогда по закону Ома:
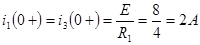 . .
Напряжения на сопротивлениях R1
и R2
:
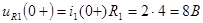 , ,
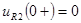 . .
Тогда напряжение на индуктивности:
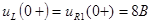 . .
Контроль вычислений.
Формулы для контроля вычислений:
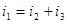 ; ; 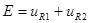 ; ; 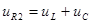 . .
Тогда:
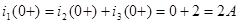 |
1-ый закон Кирхгофа выполняется |
 |
2-ой закон Кирхгофа для 1-го и 2-го контуров выполняется. |
2.1.3 Расчёт конечных условий 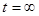
После окончания переходного процесса все токи и напряжения в схеме (рисунок 2.1) будут постоянными. Тогда ёмкость Cв эквивалентной схеме заменяется разрывом, а индуктивность L перемычкой (рисунок 2.3).
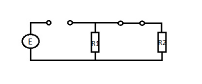
Рис. 2.3 Эквивалентная схема цепи для времени 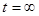 . .

Контроль вычислений.
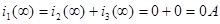 |
1-ый закон Кирхгофа выполняется |
 |
2-ой закон Кирхгофа для 1-го и 2-го контуров выполняется. |
Таблица 2.2 Результаты вычислений
| t |
0 – |
0+ |
¥ |
| i1
, A |
0 |
2 |
0 |
| i2
, A |
0 |
0 |
0 |
| i3
, A |
0 |
2 |
0 |
| uL
, B |
0 |
8 |
0 |
| uС
, B |
0 |
0 |
8 |
| uR1
, B |
0 |
8 |
0 |
| uR2
, B |
0 |
0 |
0 |
С учетом НУ и КУ можно качественно построить графики (рисунок 2.4).

Рис. 2.4 Качественные графики.
2.2 Определение переходных процессов классическим методом
В приведенной схеме (рисунок 2.1) определить классическим методом напряжения и токи переходного процесса. Построить графики переходных процессов.
2.2.1 Решение дифференциального уравнения для тока на емкости

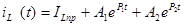
Принужденная составляющая тока на индуктивности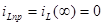 , поэтому , поэтому
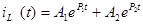
2.2.2 Определение корней 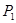 и и 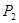
Для определения корней характеристического уравнения 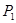 и и 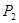 составляется эквивалентная операторная схема цепи (рисунок 2.5), далее находится операторное входное сопротивление и приравнивается к нулю ( составляется эквивалентная операторная схема цепи (рисунок 2.5), далее находится операторное входное сопротивление и приравнивается к нулю (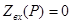 ). ).

Рисунок 2.5 Эквивалентная операторная схема цепи.
Операторное сопротивление емкости 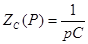 , а индуктивности , а индуктивности  , тогда , тогда
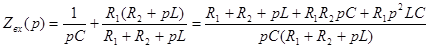
Условие 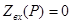 выполняется, если числитель равен нулю: выполняется, если числитель равен нулю:
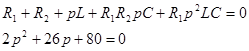
корни этого уравнения:
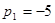 ; ;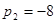
Подставим значения 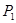 и и 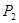 в уравнение для в уравнение для 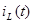 : :
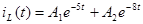
2.2.3 Определение произвольных постоянных 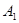 и и 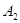
Используем значение самой функции 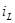 и ее производной и ее производной 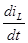 при при 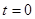 , т.е. учтем начальные условия. Учитывая, что , т.е. учтем начальные условия. Учитывая, что 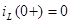 : :
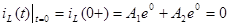 , ,
откуда получаем первое уравнение для нахождения произвольных постоянных:
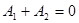
Для получения второго уравнения найдем (при 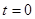 ) значение ) значение 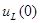 : :

откуда получаем второе уравнение для нахождения произвольных постоянных:
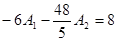
Совместное решение двух уравнений


дает значения произвольных постоянных:
После подстановки произвольных постоянных в выражение для 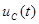 получаем: получаем:
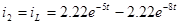
Контроль вычислений
При 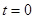 , , 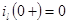
При 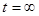 , , 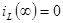
Это соответствует данным таблицы 1.
Расчет остальных токов и напряжений:
A
)
Напряжение
 : :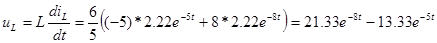 . .
Контроль вычислений: 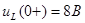 ; ; 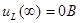 . .
Б
)Напряжение 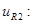
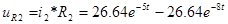
Контроль вычислений: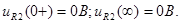
В)
Напряжение 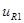 : :
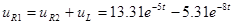 . .
Контроль вычислений: 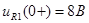 ; ; 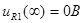 . .
Г)
Ток 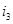 : :
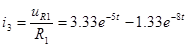 . .
Контроль вычислений: 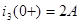 ; ; 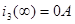 . .
Д)
Ток 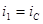 : :
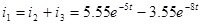 . .
Контроль вычислений: 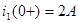 ; ; 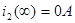 . .
Е)
Напряжение 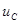 : :
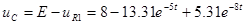 . .
Контроль вычислений: 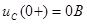 ; ; 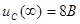 . .
Результаты вычислений:
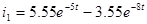 , ,
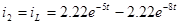 , ,
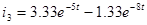 , ,
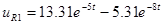 , ,
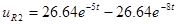 , ,
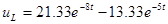 , ,
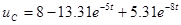 . .
2.3 Построение графиков
электрическая цепь операторный
Для построения графиков переходного процесса воспользуемся ЭВМ.

Рис. 2.6 Зависимость тока
i
1 от времени.

Рис. 2.7 Зависимость тока
iL
от времени.

Рис. 2.8 зависимость тока
i
3 от времени.

Рис. 2.9 Зависимость напряжения на ёмкости
U
с от времени.

Рис. 2.10 Зависимость напряжения на индуктивности
UL
от времени.

Рис. 2.11 Зависимость напряжения на резисторе
UR
1 от времени.

Рис. 2.12 Зависимость напряжения на резисторе
UR
2 от времени.
2.4 Расчет графиков переходного процесса
А)Определение экстремумов и точки перегиба  . .
Наиболее сложную форму имеет график 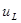 Для него необходимо рассчитать экстремум и точку перегиба. Для него необходимо рассчитать экстремум и точку перегиба.
Продифференцируем выражение
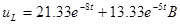 , ,
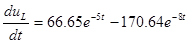 . .
Найдем значение производной при 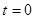 : :
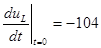 . .
Производная для 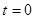 меньше нуля , следовательно кривая меньше нуля , следовательно кривая  в окрестности данной точки убывает. в окрестности данной точки убывает.
Приравняем производную 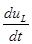 нулю и найдем максимальное значение функции: нулю и найдем максимальное значение функции:

Максимум напряжения функция принимает при 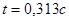 . .
Найдем точку перегиба кривой  . Для этого определим вторую производную и приравняем ее к нулю: . Для этого определим вторую производную и приравняем ее к нулю:
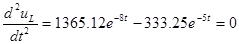 , ,
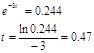
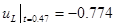
График для 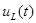 приведен ниже. приведен ниже.

Рисунок 2.13 График переходного процесса напряжения на катушке.
Определим и построим (качественно) график переходного процесса для тока через индуктивность:
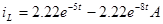
Начальные и конечные значения известны: 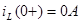 , , 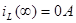 . .
Найдем экстремальное значение 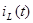 : :
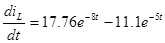 . .
При 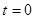 производная производная 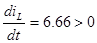 (имеет положительное значение ), т.е. кривая i(t) при (имеет положительное значение ), т.е. кривая i(t) при 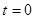 от значения от значения 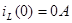 пойдет вверх. пойдет вверх.
Приравняем производную 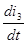 нулю и найдем максимальное значение функции: нулю и найдем максимальное значение функции:
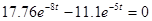
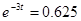
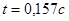
Максимум тока 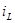 функция принимает при функция принимает при 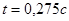 . .
Определим вторую производную и приравняв ее к нулю найдем точку перегиба тока 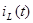 : :
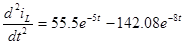 , ,
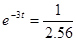
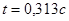 , ,
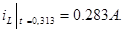
Максимум напряжения 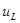 совпал с точкой перегиба кривой совпал с точкой перегиба кривой 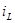 при при 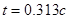 . .
График для 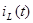 приведен ниже. приведен ниже.

Рисунок 2.14 График переходного процесса тока на индуктивности.
2.5 Обобщенные характеристики цепи
Определим обобщенные характеристики цепи:
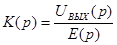 , , 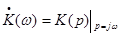 , , 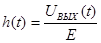 , , 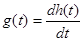 . .
Для схемы такой структуры коэффициент передачи можно найти по типовой формуле. Он будет равен
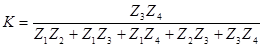 . .
Для заданной схемы

Найдём изображение переходной характеристики H(p):
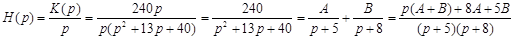 ; ;
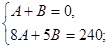 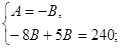 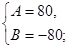
Тогда
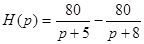 ; ;
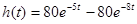
Найдем предельные значения переходной характеристики:
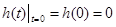 ; ; 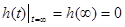
Определим импульсную характеристику цепи g(t).
Ее можно найти двумя методами:
Первый: дифференцируя значение h(t):
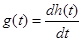 ; ;
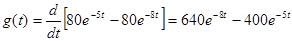
Второй: по изображению импульсной характеристики G(р):
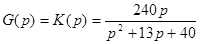
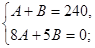 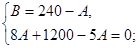 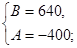
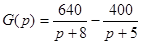
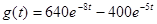
Определим комплексный коэффициент передачи 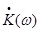 : :
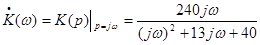
Предельные значения:
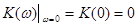 , , 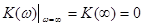 . .
Графики переходной, импульсной характеристик и комплексного коэффициента передачи представлены на рисунках 2.14-2.16.

Рисунок 2.15. График функции переходной характеристики
h
(
t
).

Рисунок 2.16. График функции импульсной характеристики
g
(
t
).
Данная курсовая работа помогает закрепить знания о переходных процессах в электрических цепях и наглядно увидеть физическую природу явления. В результате проделанной работы были практически рассчитаны начальные и конечные значения всех токов и напряжений в цепи,и построены графики изменения токов и напряжений, а так же графики функций переходной и импульсной характеристик.
При написании данной работы использовались программные пакеты и системы моделирования, такие как:
· Microsoft Office 2007
· Advanced Grapher
· Paint
При переходных процессах могут возникать большие перенапряжения, сверхтоки, электромагнитные колебания, которые могут нарушить работу устройства вплоть до выхода его из строя. С другой стороны, переходные процессы находят полезное практическое применение, например, в различного рода электронных генераторах. А значит проделанная работа имеет не только теоретическую ценность, но и не малое значение при расчете той или иной конкретной практической задачи.
Список использованной литературы
1. Белов С.П., Прохоренко Е.И. «Учебно-методическое пособие по расчету переходных процессов в электрических цепях для студентов специальностей 210406 «Сети связи и системы коммутации» и 210405 «Радиосвязь, радиовещание и телевидение». Изд-во БелГУ. Белгород 2006.
2. Фриск В.В. «Основы теории цепей». Солон-Пресс. Москва 2004.
3. Бычков Ю.А., Золотницкий В.М., Чернышев Э.П. «Основы теории электрических цепей». Лань. Москва 2002.
|