МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
Учреждение образования
«Витебский государственный технологический университет»
Кафедра экономики
КОНТРОЛЬАЯ РАБОТА
по дисциплине «Статистика»
ВАРИАНТ № 6
Задание № 1
Используя данные статистического наблюдения о производительности труда рабочих, провести статистическое исследование:
1) Исходный эмпирический ряд преобразовать в дискретный и интервальный и по каждому из них (вариационному, дискретному и интервальному), рассчитать среднюю величину.
2) По дискретному ряду исчислить среднюю величину с использованием её свойств.
3) По интервальному ряду определить моду и медиану.
4) По дискретному ряду рассчитать показатели вариации:
– размах,
– среднее линейное отклонение,
– дисперсию,
– среднее квадратическое отклонение,
– коэффициент осцилляции,
– относительное линейное отклонение,
– коэффициент вариации.
№
раб.
|
Количество вырабатываемых деталей одним рабочим за месяц, ед. |
№
раб.
|
Количество вырабатываемых деталей одним рабочим за месяц, ед. |
| 1 |
216 |
21 |
192 |
| 2 |
168 |
22 |
144 |
| 3 |
192 |
23 |
144 |
| 4 |
120 |
24 |
120 |
| 5 |
216 |
25 |
120 |
| 6 |
120 |
26 |
120 |
| 7 |
168 |
27 |
120 |
| 8 |
120 |
28 |
168 |
| 9 |
144 |
29 |
216 |
| 10 |
120 |
30 |
120 |
| 11 |
192 |
31 |
120 |
| 12 |
120 |
32 |
192 |
| 13 |
144 |
33 |
120 |
| 14 |
168 |
34 |
144 |
| 15 |
168 |
35 |
120 |
| 16 |
120 |
36 |
120 |
| 17 |
120 |
37 |
120 |
| 18 |
216 |
38 |
120 |
| 19 |
216 |
39 |
192 |
| 20 |
120 |
40 |
120 |
Решение задания 1
1)
Для нахождения средней величины вариационного
ряда воспользуемся формулой:
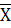 = = 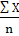 ; ; 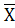 = = 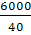 = 150 (деталей) = 150 (деталей)
где ∑Х – это сумма всех деталей, вырабатываемых рабочими за месяц,
n – количество рабочих.
Рассчитаем среднюю величину для дискретного
ряда:
| Выработка рабочего, Х |
Число рабочих, f |
Хf |
| 120 |
20 |
2400 |
| 144 |
5 |
720 |
| 168 |
5 |
840 |
| 192 |
5 |
960 |
| 216 |
5 |
1080 |
| åf=40 |
åХf=6000 |
Рассчитываем среднюю арифметическую взвешенную по сгруппированным данным, используя формулу:
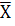 = = 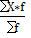 ; ; 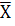 = = 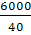 = 150 (деталей) = 150 (деталей)
Далее для интервального
ряда определяем число групп с использованием формулы Стерджесса:
n = 1 + 3,322 lgN; n = 1 + 3,322 lg 40 = 5,92 (≈ 6 групп)
где n – число групп, N – число единиц совокупности (40).
Затем определяем величину интервала (h) по формуле:
h =  = = 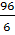 = 16 (деталей) = 16 (деталей)
И используя таблицу, рассчитываем среднюю величину:
| Группы рабочих по уровню выработки, Х |
Количество рабочих в группе, f |
Центр интервала, Х¢ |
Х¢f |
| 120 – 136 |
20 |
128 |
2560 |
| 136 – 152 |
5 |
144 |
720 |
| 152 – 168 |
0 |
160 |
0 |
| 168 – 184 |
5 |
176 |
880 |
| 184 – 200 |
5 |
190 |
950 |
| 200 – 216 |
5 |
208 |
1040 |
| å f=40 |
å Х¢f=6150 |
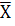 = = 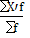 , , 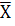 = = 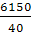 = 153,8 (деталей) = 153,8 (деталей)
2)
По дискретному ряду исчисляем среднюю величину с использованием её свойств, в том числе по «способу моментов»:
| Выработка рабочего, Х |
Число
рабочих, f
|
Хf |
Х–Х0
Х0
= 168
|
А = 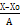
А = 24
|

b = 5
|
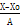 * *  |
| 120 |
20 |
2400 |
-48 |
-2 |
4 |
-8 |
| 144 |
5 |
720 |
-24 |
-1 |
1 |
-1 |
| 168 |
5 |
840 |
0 |
0 |
1 |
0 |
| 192 |
5 |
960 |
24 |
1 |
1 |
1 |
| 216 |
5 |
1080 |
48 |
2 |
1 |
2 |
| åf=40 |
åХf=6000 |
å =8 =8 |
å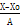 * *  = -6 = -6 |
Определяем среднюю величину по «способу моментов»:
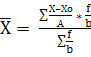 * А + Х0
, * А + Х0
, 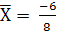 * 24 + 168 = 150 (деталей) * 24 + 168 = 150 (деталей)
3)
Для определения моды (Mo) по интервальному ряду, вначале находим ширину модального интервала (iMo
):
iMo
= 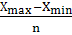 , iMo
= , iMo
= 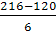 = 16, = 16,
а затем рассчитываем моду по формуле:
Mo=xMo
+ iMo
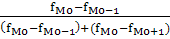
где хMo
– начальная граница модального интервала (120),
iMo
– ширина модального интервала (16),
fMo
– частота модального интервала (20),
fMo
-1
–частота интервала, предшествующего модальному (0),
fMo
+1
– частота интервала, следующего за модальным (5).
| Группы рабочих по уровню выработки, Х |
Количество рабочих
в группе, f
|
| 120 – 136 |
20 |
– модальный интервал |
| 136 – 152 |
5 |
| 152 – 168 |
0 |
| 168 – 184 |
5 |
| 184 – 200 |
5 |
| 200 – 216 |
5 |
Mо=120+ 16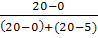 = 129 (деталей) = 129 (деталей)
Для расчета медианы по интервальному ряду, вначале определяем медианный интервал по способу накопления частот:
| Х |
f |
SMe
|
| 120 – 136 |
20 |
20 |
| 136 – 152 |
5 |
| 152 – 168 |
0 |
| 168 – 184 |
5 |
| 184 – 200 |
5 |
| å f=40 |
Медиану находим по формуле:
Me = XMe
+ iM
е
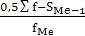 , Me =120 + 16 , Me =120 + 16 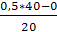 = 136 = 136
где XMe
– начальная граница медианного интервала (120),
iM
е
– ширина медианного интервала (16),
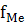 – частота медианного интервала (20), – частота медианного интервала (20),
SM
е-1 –
сумма накопленных частот интервала, предшествующего медианному (0),
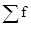 – сумма всех частот ряда (40), – сумма всех частот ряда (40),
4)
Рассчитываем показатели вариации по дискретному ряду:
Выработка
рабочего, x
|
Число
рабочих, f
|
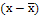 |
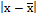 f f |
(x–x)2
|
(x–x)2
f |
х2
|
х2
f |
| 120 |
20 |
-30 |
600 |
900 |
18000 |
14400 |
288000 |
| 144 |
5 |
-6 |
30 |
36 |
180 |
20736 |
103680 |
| 168 |
5 |
18 |
90 |
324 |
1620 |
28224 |
141120 |
| 192 |
5 |
42 |
210 |
1764 |
8820 |
36864 |
184320 |
| 216 |
5 |
66 |
330 |
4356 |
21780 |
46656 |
233280 |
| åf=40 |
å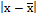 f=1260 f=1260 |
å(х-х)2
f=50400 |
х2
f=950400 |
1) Размах R = xmax
– xmin
, R = 216 – 120 = 96 (деталей)
2) Среднее линейное отклонение 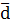 = =
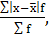 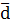 = =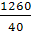 = 31,5 = 31,5
3) Дисперсия 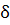 2
= 2
=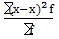 , , 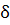 2
= 2
= 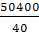 = 1260 = 1260
4) Среднее квадратическое отклонение 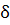 = =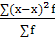 = =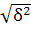 , , 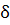 = =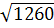 =35,496 ≈ 36 =35,496 ≈ 36
5) Коэффициент осцилляции KR
=  * 100, KR
= * 100, KR
= 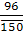 * 100 = 64 % * 100 = 64 %
6) Относительное линейное отклонение Kе
=  * 100 %, Kе
= * 100 %, Kе
= 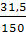 = 21 % = 21 %
7) Коэффициент вариации V =  * 100, V = * 100, V = 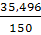 = 23,664 % = 23,664 %
Задание № 2
Используя статистическую информацию, приведенную в таблице, проанализировать динамику объема продукции по двум родственным организациям:
1) по организации № 1 исчислить цепные показатели динамики;
2) по организации № 2 исчислить базисные показатели динамики;
3) методом аналитического выравнивания установить общую тенденцию (определить тренд) изменения объема продукции:
3.1) по организации № 1 – за 6 лет;
3.2) по организации № 2 – за последние 5 лет.
4) По каждому заданию сделать развернутые выводы.
5) Сравнить динамику выпуска продукции по двум организациям.
| № организации |
Выпуск продукции по годам, тыс. шт. |
| 2002
|
2003
|
2004
|
2005
|
2006
|
2007
|
| 1 |
520 |
550 |
560 |
620 |
640 |
700 |
| 2 |
700 |
750 |
780 |
800 |
820 |
830 |
Решение задания 2
1)
Исчисляем цепные показатели динамики по организации № 1:
Наименование
показателей
|
Ед.
изм.
|
Формулы |
Уровни показателей по годам |
| 2002
|
2003
|
2004
|
2005
|
2006
|
2007
|
Выпуск
продукции
|
тыс. шт. |
520 |
550 |
560 |
620 |
640 |
700 |
| Аналитические показатели динамики: |
– абсолютный
прирост
|
тыс. шт. |
∆yц
= yi
– yi-1
|
– |
30 |
10 |
60 |
20 |
60 |
| – темп роста |
% |
Трц
= 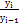 |
– |
105,8 |
101,8 |
110,7 |
103,2 |
109,4 |
– темп
прироста
|
% |
Тпрц
= 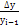 |
– |
5,8 |
1,8 |
10,7 |
3,2 |
9,4 |
– вес 1%
прироста
|
тыс. шт. |
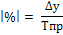 |
– |
5,2 |
5,5 |
5,6 |
6,2 |
6,4 |
| Средние показатели динамики: |
– средний
уровень
ряда динамики
|
тыс. шт. |
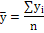 |
598,3 |
– средний
абсолютный прирост
|
тыс. шт. |
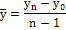 |
36 |
– средний
темп роста
|
% |
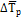 = = 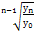 |
1,061 или 106,1% |
– средний
темп прироста
|
% |
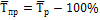 |
6,1% |
дискретный интервальный эмпирический вариация
Выводы: выпуск продукции в 2003 году по сравнению с 2002 повысился на 30 тыс.шт., т.е. как мы видим по темпам роста в 1,058 раза или на 5,8%, а 1% прироста давал увеличение продукции на 5,172 тыс.шт.
В 2004 году по сравнению с 2003 выпуск продукции повысился на 10 тыс.шт., т.е. в 1,018 раза или на 1,8%, а 1% прироста давал увеличение продукции на 5,556 тыс.шт.
В 2005 году по сравнению с 2004 выпуск продукции повысился на 60 тыс.шт., т.е. в 1,107 раза или на 10,7%, а 1% прироста давал увеличение продукции на 5,607 тыс.шт.
В 2006 году по сравнению с 2005 выпуск продукции повысился на 20 тыс.шт., т.е. в 1,032 раза или на 3,2%, а 1% прироста давал увеличение продукции на 6,25 тыс.шт.
В 2007 году по сравнению с 2006 выпуск продукции повысился на 60 тыс.шт., т.е. в 1,094 раза или на 9,4%, а 1% прироста давал увеличение продукции на 6,383 тыс.шт.
В течение периода с 2002 г. по 2007 г. в организации №1 согласно расчетам наблюдается увеличение выпуска продукции, средний темп прироста составляет +6,1%, а средний абсолютный прирост +36 тыс.шт.
2)
Исчисляем базисные показатели динамики по организации № 2:
Наименование
показателей
|
Ед.
изм.
|
Формулы |
Уровни показателей по годам |
| 2002
|
2003
|
2004
|
2005
|
2006
|
2007
|
Выпуск
продукции
|
тыс. шт. |
700 |
750 |
780 |
800 |
820 |
830 |
| Аналитические показатели динамики: |
– абсолютный
прирост
|
тыс. шт. |
∆yб
= yi
– y0
|
– |
50 |
80 |
100 |
120 |
130 |
| – темп роста |
% |
Трб
=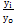 * 100% * 100% |
100,0 |
107,1 |
111,4 |
114,3 |
117,1 |
118,6 |
– темп
прироста
|
% |
Трб
= 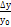 * 100% * 100% |
– |
7,1 |
11,4 |
14,3 |
17,1 |
18,6 |
Выводы: выпуск продукции в 2003 году по сравнению с 2002 повысился на 50 тыс.шт., т.е. как мы видим по темпам роста в 1,071 раза или на 7,1%. В 2004 году по сравнению с 2002 выпуск продукции увеличился на 80 тыс.шт., т.е. в 1,114 раза или на 11,4%. В 2005 году по сравнению с 2002 происходит увеличение объема выпуска продукции на 100 тыс.шт., т.е. в 1,143 раза или на 14,3%. В 2006 году по сравнению с базисным периодом (2002 г) увеличивается выпуск продукции на 120 тыс. шт., т.е. в 1,171 раза или на 17,1%. В 2007 году по сравнению с 2002 также объем выпуска продукции увеличивается 130 тыс.шт., т.е. в 1,186 раза или на 18,6%.
В течение периода с 2002 г. по 2007 г. в организации №2 согласно расчетам наблюдается повышение выпуска продукции, средний темп прироста составляет 13,6%, а средний абсолютный прирост 96 тыс.шт.
3)
Определяем общую тенденцию способом аналитического выравнивания ряда динамики следующим образом:
– выбор математической модели развития явления во времени;
– определение параметров уравнения (тренда) %;
– экономическая интерпретация найденного тренда;
– графическая обработка результатов аналитического выравнивания
Абсолютный прирост уровней ряда происходит в арифметической прогрессии, следовательно, выравнивание ряда динамики следует производить по прямой: 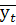 = = 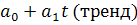
где: 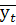 – выровненные (теоретические ) уровни ряда; – выровненные (теоретические ) уровни ряда;
 , ,
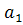 – параметры уравнения; t – условное обозначение времени. – параметры уравнения; t – условное обозначение времени.
Установим общую тенденцию (определим тренд) изменения объема продукции по организации № 1 за 6 лет.
Поскольку используется ряд с четным количеством периодов, то:
| Значение t |
2002 |
2003 |
2004 |
2005 |
2006 |
2007 |
| åt = 0 |
- 5 |
- 3 |
- 1 |
1 |
3 |
5 |
При упрощенном способе расчетов, когда ∑t = 0, параметры прямой определяются по формулам:
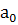 = =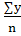 , , 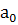 = =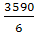 = 598,333; = 598,333; 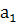 = = 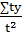 , , 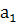 = = 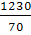 = 17,571. = 17,571.
где у –исходный уровень ряда динамики;
n – количество периодов ряда.
Уравнение прямой (тренда) будет иметь вид: 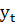 = 598,333+17,571t = 598,333+17,571t
| Расчетная таблица выравнивания ряда по прямой для организации № 1: |
| Годы |
Прибыль
тыс. руб.
(у)
|
Абсолютный прирост,
тыс. руб.
(Dу)
|
t |
t2
|
tу
|
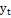 |
Скорость ряда
(разница теоретических уровней)
|
| 2002 |
520 |
–– |
-5 |
25 |
-2600 |
510,45 |
| 2003 |
550 |
30 |
-3 |
9 |
-1650 |
545,59 |
| 2004 |
560 |
10 |
-1 |
1 |
-560 |
580,73 |
| 2005 |
620 |
60 |
1 |
1 |
620 |
615,87 |
| 2006 |
640 |
20 |
3 |
9 |
1920 |
651,01 |
| 2007 |
700 |
60 |
5 |
25 |
3500 |
686,15 |
| ∑у=3590 |
∑t=0 |
∑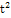 =70 =70 |
∑tу=1230 |
∑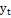 =3589,8 =3589,8 |
Рассчитаем теоретические уровни ряда динамики:
598,333 + 17,571 * (-5) = 598,333 + (- 87,855) = 510,478
598,333 + 17,571 * (-3) = 598,333 + (- 52,713) = 545,62
598,333 + 17,571 * (-1) = 598,333 + (- 17,571) = 580,762
598,333 + 17,571 * 1 = 615,904
598,333 + 17,571 * 3 = 598,333 + 52,713 = 651,046
598,333 + 17,571 * 5 = 598,333 + 87,855 = 686,188
Поскольку 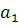 имеет знак «+», то наблюдается тенденция роста. имеет знак «+», то наблюдается тенденция роста.
Определяем скорость ряда для экономической интерпретации найденного тренда, которая при четном количестве периодов времени (6), будет равна:
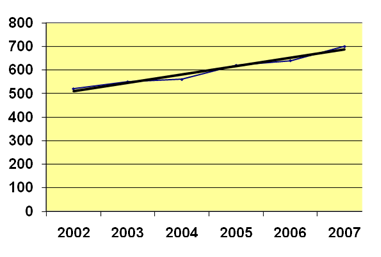
2 *  = 2 * 17,571 = 35,142 = 2 * 17,571 = 35,142
Полученный тренд свидетельствует о наличии положительной тенденции в измерении выпуска продукции (а1
> 0), так как в среднем за год выпуск составил 598,333 тыс. шт., то среднегодовой рост объема выпуска продукции за этот период составляет 35,142 тыс. шт:
Определяем тренд изменения объема продукции по организации № 2 за последние 5 лет, используя ряд с нечетным количеством периодов:
| Значение t |
2003 |
2004 |
2005 |
2006 |
2007 |
| åt = 0 |
- 2 |
- 1 |
0 |
1 |
2 |
При упрощенном способе расчетов параметры прямой определяются по формулам:
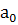 = =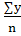 , , 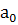 = =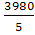 = 796; = 796;
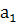 = = 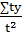 , , 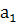 = = 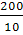 = 20. = 20.
Уравнение прямой (тренда) будет иметь вид:
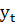 = 796 + 20t = 796 + 20t
где у –исходный уровень ряда динамики;
n – количество периодов ряда.
| Расчетная таблица выравнивания ряда по прямой для организации № 2: |
| Годы |
Прибыль
тыс. руб.
(у)
|
Абсолютный прирост,
тыс. руб.
(Dу)
|
t |
t2
|
tу
|
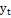 |
Скорость ряда
(разница теоретических уровней)
|
| 2003 |
750 |
50 |
-2 |
4 |
-100 |
756 |
| 2004 |
780 |
80 |
-1 |
1 |
-80 |
776 |
| 2005 |
800 |
100 |
0 |
0 |
0 |
796 |
| 2006 |
820 |
120 |
1 |
1 |
120 |
816 |
| 2007 |
830 |
130 |
2 |
4 |
260 |
836 |
| ∑у=3980 |
∑t=0 |
∑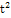 =10 =10 |
∑tу=200 |
∑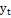 =3980 =3980 |
Рассчитаем теоретические уровни ряда динамики:
796 + 20 * (-2) = 796 + (- 40) = 756
796 + 20 * (-1) = 796 + (- 20) = 776
796 + 20 * 0 = 796
796 + 20 * 1 = 816
796 + 20 * 2 = 796 + 40 = 836
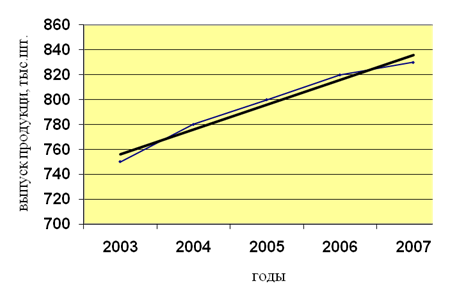
Поскольку 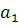 имеет знак «+», то наблюдается тенденция роста имеет знак «+», то наблюдается тенденция роста
Определяем скорость ряда для экономической интерпретации найденного тренда, которая при нечетном количестве периодов времени (5), будет равна параметру а1
, т.е. 20 тыс.шт.
Полученный тренд свидетельствует о наличии положительной тенденции в измерении выпуска продукции (а1
> 0), если в среднем за год выпуск составил 796 тыс. шт., то его прирост из года в год за исследуемые 5 лет в среднем составляет 20 тыс. шт.:
5)
Чтобы сравнить динамику выпуска продукции по двум организациям, необходимо применить способ приведения рядов динамики к единому основанию и исчислить коэффициент опережения:
| Годы |
Выпуск продукции, тыс. шт.
|
| Организация № 1 |
Организация № 2 |
| 2002
|
520 |
700 |
| 2003
|
550 |
750 |
| 2004
|
560 |
780 |
| 2005
|
620 |
800 |
| 2006
|
640 |
820 |
| 2007
|
700 |
830 |
Из таблицы видно, что выпуск продукции по двум организациям происходит неравномерно.
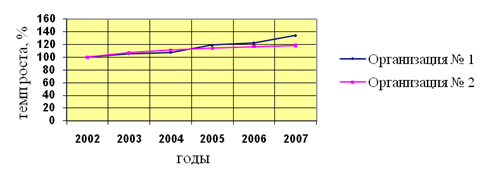
Приведем ряды динамики к единому основанию, т.е. все уровни выразим в процентах к начальному уровню.
Тогда ряд динамики преобразуется в ряд динамики, состоящий из базисных уровней темпов роста:
| Годы |
Базисные темпы роста, % |
| Организация № 1 |
Организация № 2 |
| 2002
|
100 |
100,0 |
| 2003
|
105,7 |
107,1 |
| 2004
|
107,6 |
111,4 |
| 2005
|
119,2 |
114,3 |
| 2006
|
123,0 |
117,1 |
| 2007
|
134,6 |
118,6 |
Следовательно, выпуск продукции в организации № 1 с 2003 – 2004 г. растет медленнее, чем в организации № 2, а с 2005 – 2007 г. растет быстрее, чем в организации № 2.
Для сравнения рассчитаем коэффициенты опережения (Копер
.)
Копер.2004
= 107,6/111,4 = 0,966
Копер.2007
= 134,6/118,6 = 1,135
При сравнении организации № 1 и организации № 2 можно сделать следующие выводы: выпуск продукции в организации № 1 с 2003-2004 г. растет медленнее в 0,966 раз, а с 2005-2007 растет быстрее в 1,135 раз:
Задание № 3
Используя индексный метод по данным, приведенным в таблице, проанализировать деятельность организации:
1. Определить, как изменились издержки организации в отчётном периоде по сравнению с базисным и как повлияло на эти изменение:
1.1) изменение объёма выпускаемой продукции;
1.2) изменение себестоимости единицы продукции;
Показать связь индексов и дать развернутый вывод.
2. Определить индексы средней цены изделия переменного, фиксированного (постоянного) состава и структурных сдвигов.
Сделать развёрнутый вывод об изменении средней цены единицы продукции и его причинах.
Виды
изделий
|
Выпуск продукции,
тыс. ед.
|
Цена единицы
продукции, тыс. руб.
|
Себестоимость ед. продукции, тыс. руб.
|
| базисный период |
отчетный период |
базисный период |
отчетный период |
базисный период |
отчетный период |
| 1
|
3
|
4
|
5
|
6
|
7
|
8
|
А
Б
В
|
150
160
180
|
180
180
200
|
32
28
45
|
25
30
42
|
20
18
28
|
18
19
27
|
Решение задания 3
При выполнении первого пункта задания целесообразно использование таблицы следующей формы:
Виды
продукции
|
Выпуск
продукции,
тыс. ед.
|
Себестоимость
единицы
продукции,
тыс. руб.
|
Издержки, млн. руб.
|
q1
z0
|
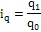 |
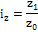 |
базис.
период
|
отчет.
период
|
базис.
период
|
отчет.
период
|
базисный
период
|
отчетный
период
|
| q 0
|
q1
|
z0
|
z1
|
q0
z0
|
q1
z1
|
| А |
150 |
180 |
20 |
18 |
3000 |
3240 |
3600 |
1,2 |
0,9 |
| Б |
160 |
180 |
18 |
19 |
2880 |
3420 |
3240 |
1,125 |
0,055 |
| В |
180 |
200 |
28 |
27 |
5040 |
5400 |
5600 |
1,111 |
0,964 |
| Итого: |
åq0
z0
=10920 |
åq1
z1
=12060 |
åq1
z0
=12440 |
Для того, чтобы определить, как изменились издержки организации в отчетном периоде по сравнению с базисным, следует рассчитать агрегатный индекс издержек (себестоимость всей продукции по организации):
Iz
= 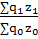 , Iz
= , Iz
= 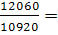 1,1044 раз или + 10,4 % 1,1044 раз или + 10,4 %
Агрегатный индекс издержек показывает относительное изменение издержек организации. Можно рассчитать абсолютное изменение издержек (в рублях):
∆z =∑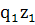 – ∑ – ∑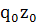 , ∆z = 12060 – 10920 = 1140 (млн.рублей) , ∆z = 12060 – 10920 = 1140 (млн.рублей)
Индекс издержек организации показывает изменение показателя издержек организации за счет объема выпускаемой продукции, и за счет себестоимости единицы продукции.
При использовании индексного метода проводится факторинговый анализ и оценивается обособленное влияние каждого из этих факторов:
Изменение издержек организации за счет изменения объема выпускаемой продукции рассчитывается по формуле:
Iq
= 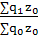 , Iq
= , Iq
= 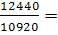 1,1392или + 13,92 % 1,1392или + 13,92 %
∆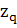 = ∑ = ∑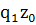 – ∑ – ∑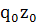 , , 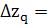 12440-10920=1520 (млн.рублей) 12440-10920=1520 (млн.рублей)
Изменение издержек за счет изменения себестоимости единицы продукции рассчитывается по формуле:
Iz
=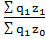 , Iz
= , Iz
=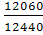 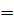 0,9695 или - 3,1 % 0,9695 или - 3,1 %
∆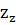 = ∑ = ∑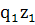 – ∑ – ∑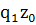 , , 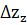 = 12060 – 12440 – -380 (млн.рублей) = 12060 – 12440 – -380 (млн.рублей)
Таким образом, издержки организации в отчетном периоде по сравнению с базисным увеличились на 10,4 % или на 1140 млн.рублей. За счет увеличения объема выпускаемой продукции издержки выросли на 13,9 % или на 1520 млн.рублей и за счет уменьшения себестоимости единицы продукции издержки уменьшились на 3,1% или на 380 млн.рублей произошло это изменение.
В отчетном периоде по сравнению с базисным, объем выпускаемой продукции А увеличился на 20%, продукции Б – на 12,5% и продукции В – на 11,1%.
Себестоимость единицы продукции А в отчетном периоде по сравнению с базисным выросла на 10 %; себестоимость единицы продукции Б выросла на 5,6 %, а единица продукции В снизилась на 3,6 %.
Для расчёта индексов средней цены используем следующую таблицу:
| Виды продукции |
Выпуск
продукции,
тыс. ед.
|
Цена
ед.продукции, тыс. руб.
|
p0
q0
|
p1
q1
|
p0
q1
|
d0
=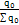 |
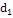 = =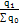 |
p0
d0
|
p1
d1
|
p0
d1
|
базисный
период,
q0
|
отчётный
период,
q1
|
базисный
период, p0
|
отчётный
период, p1
|
| А |
150 |
180 |
32 |
25 |
4800 |
4500 |
5760 |
0,306 |
0,321 |
9,796 |
8,036 |
10,286 |
| Б |
160 |
180 |
28 |
30 |
4480 |
5400 |
5040 |
0,327 |
0,321 |
9,143 |
9,643 |
9,000 |
| В |
180 |
200 |
45 |
42 |
8100 |
8400 |
9000 |
0,367 |
0,357 |
16,531 |
15,000 |
16,531 |
∑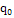 =490 =490 |
∑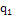 =560 =560 |
105 |
97 |
∑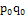
=17380
|
∑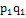
=18300
|
∑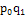
=19800
|
∑d0
=1 |
∑d1
=1 |
∑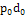
=35,47
|
∑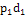
=32,68
|
∑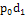 =35,82 =35,82 |
Рассчитываем индекс переменного состава средней цены изделия по формуле:
Iрп.с.
= 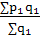 ÷ ÷ 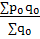 , Iрп.с.
= , Iрп.с.
= 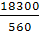 ÷ ÷ 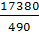 = 0,9213 (- 7,87 %) = 0,9213 (- 7,87 %)
или
Iрп.с.
= 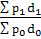 , Iрп.с.
= , Iрп.с.
= 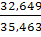 = 0,9213 (- 7,87 %) = 0,9213 (- 7,87 %)
Далее исчисляем индекс фиксированного состава:
Iрф.с.
= 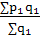 ÷ ÷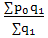 , ,
Iрф.с.
= 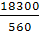 ÷ ÷ 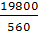 = 0,9242 (- 7,58 %) = 0,9242 (- 7,58 %)
Или
Iрф.с.
= 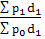 , ,
Iрф.с.
= 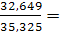 0,9242(- 7,58 %) 0,9242(- 7,58 %)
Затем индекс структурных сдвигов:
Iрс.с.
= 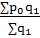 ÷ ÷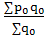 , ,
Iрс.с.
= 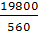 ÷ ÷ 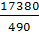 = 0,9968 (- 0,32 %) = 0,9968 (- 0,32 %)
Или
Iрс.с.
=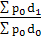 , ,
Iрс.с.
= 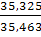 = 0,9968 (- 0,32 %) = 0,9968 (- 0,32 %)
Из этого следует, что средняя цена единицы продукции в отчетном периоде по сравнению с базисным уменьшилась на 7,87 %.
Это вызвано непосредственным падением цен на анализируемую продукцию. Индекс фиксированного состава показывает, что непосредственное изменение цен составило их уменьшение на 7,58 %.
Одновременно наблюдается отрицательное влияние на изменение средней цены фактора структурных сдвигов.
Увеличение в отчетном периоде продукции А и Б, которые имеют более низкую цену, при одновременном уменьшении количества продукции В, имеющей более высокую цену, приводит к снижению средней цены на 0,32%.
Задание № 4
Используя статистические данные производственной деятельности 15-ти организаций отрасли, необходимо установить наличие, характер и тесноту связи между признаком-фактором (х) и признаком-результатом (у).
Исследование зависимости между признаками необходимо провести следующими методами:
4.1) методом параллельных рядов;
4.2) методом аналитических группировок;
4.3) методом корреляционно-регрессионного анализа.
Исследование зависимости по каждому из указанных методов завершается выводом о наличии, характере и тесноте установленной связи между Х и У.
№
пр-я
|
Результативный признак
(у)
|
Факторный признак
(х)
|
| Рентабельность капитала |
Коэффициент финансовой независимости |
| 1. |
6,4 |
50,6 |
| 2. |
6,0 |
55,4 |
| 3. |
6,8 |
60,2 |
| 4. |
7,2 |
66,8 |
| 5. |
5,6 |
45,9 |
| 6. |
5,4 |
45,5 |
| 7. |
8,0 |
70,0 |
| 8. |
4,0 |
30,0 |
| 9. |
5,8 |
55,5 |
| 10. |
4,8 |
40,1 |
| 11. |
5,6 |
45,9 |
| 12. |
5,4 |
45,5 |
| 13. |
8,0 |
70,0 |
| 14. |
4,2 |
36,0 |
| 15. |
5,7 |
55,5 |
Решение задания 4
Чтобы установить зависимость по методу сравнения параллельных рядов для оценки тесноты связи, воспользуемся коэффициентом ранговой корреляции, который рассчитывается по формуле:
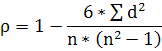
Для его определения воспользуемся таблицей:
№
предприятия
|
Признак-фактор Х |
Признак-результат У |
Ранги |
Разность
рангов, d
|
d 2
|
| Х |
У |
| 8 |
30,0 |
4,0 |
1 |
1 |
0 |
0 |
| 14 |
36,0 |
4,2 |
2 |
2 |
0 |
0 |
| 10 |
40,1 |
4,8 |
3 |
3 |
0 |
0 |
| 6 |
45,5 |
5,4 |
4,5 |
4,5 |
0 |
0 |
| 12 |
45,5 |
5,4 |
4,5 |
4,5 |
0 |
0 |
| 5 |
45,9 |
5,6 |
6,5 |
6,5 |
0 |
0 |
| 11 |
45,9 |
5,6 |
6,5 |
6,5 |
0 |
0 |
| 1 |
50,6 |
6,4 |
8 |
11 |
-3 |
9 |
| 2 |
55,4 |
6,0 |
9 |
10 |
-1 |
1 |
| 9 |
55,5 |
5,8 |
10,5 |
9 |
1,5 |
2,25 |
| 15 |
55,5 |
5,7 |
10,5 |
8 |
2,5 |
6,25 |
| 3 |
60,2 |
6,8 |
12 |
12 |
0 |
0 |
| 4 |
66,8 |
7,2 |
13 |
13 |
0 |
0 |
| 7 |
70,0 |
8,0 |
14,5 |
14,5 |
0 |
0 |
| 13 |
70,0 |
8,0 |
14,5 |
14,5 |
0 |
0 |
| å d 2
= 18,5 |
В данном случае можно сказать, что связь есть, и она прямая, поскольку с увеличением X просматривается увеличение Y.
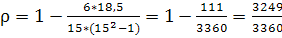 = 0,966 = 0,966
Коэффициент ранговой корреляции позволяет сделать вывод о наличии весьма тесной связи между коэффициентом финансовой независимости и рентабельностью капитала, т.к. 0,7<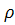 <1. <1.
Использование метода аналитических группировок предполагает предварительное определение количества групп. В данном случае количество групп равно 5.
Определим ширину интервала группировки по X:
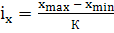 ; ; 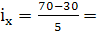 8 (при К = 5) 8 (при К = 5)
Для проведения расчетов воспользуемся таблицей:
Группы предприятий
по признаку-фактору Х
|
Количество
предприятий в группе, f
|
Сумма значений
признака-результата по всем предприятиям группы, åу
|
Среднее значение
признака-результата
по группе, `Угр
|
| 30-38 |
2 |
4,0+4,2=12,4 |
4,1 |
 38-46 38-46 |
5 |
4,8+5,4*2+5,6*2=26,8 |
 5,36 5,36 |
| 46-54 |
1 |
6,4 |
6,4 |
| 54-62 |
4 |
6,0+5,7+5,8+6,8=24,3 |
6,075 |
| 62-70 |
3 |
7,2+8,0*2=23,2 |
7,73 |
Связь между коэффициентом финансовой независимости и рентабельностью капитала прямая.
Для расчета дисперсии воспользуемся следующей таблицей:
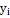 |
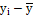 |
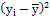 |
| 4,0 |
-1,93 |
3,73 |
| 4,2 |
-1,73 |
2,99 |
| 4,8 |
-1,13 |
1,28 |
| 5,4 |
-0,53 |
0,28 |
| 5,4 |
-0,53 |
0,28 |
| 5,6 |
-0,33 |
0,11 |
| 5,6 |
-0,33 |
0,11 |
| 6,4 |
0,47 |
0,22 |
| 6,0 |
0,07 |
0,01 |
| 5,7 |
-0,23 |
0,05 |
| 5,8 |
-0,13 |
0,02 |
| 6,8 |
0,87 |
0,76 |
| 6,8 |
0,87 |
0,76 |
| 7,2 |
1,27 |
1,61 |
| 8,0 |
2,07 |
4,29 |
| 8,0 |
2,07 |
4,29 |
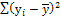 =20,79 =20,79 |
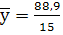 = 5,927 = 5,927
Для оценки тесноты связи рассчитаем эмпирическое корреляционное отношение:
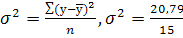 =
1,386; =
1,386;
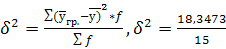 =
1,223; =
1,223;
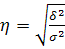 ; ;
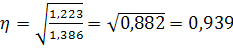
Таким образом, можно сделать вывод, что связь между исследуемыми признаками весьма тесная.
Для проведения исследования зависимости с помощью корреляционно-регрессионного анализа определим уравнение регрессии.
Если предполагается, что связь линейная (т.е. урасч.
= а0
+а1
x), то задача нахождения уравнения связи состоит в расчете таких значений коэффициентов а0
и а1
, при которых сумма квадратов отклонений расчетных значений у от фактических была бы минимальной:
 ; ; 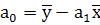
Построим таблицу следующей формы:
| x |
y |
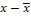 |
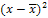 |
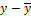 |
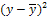 |
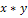 |
(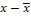 )*( )*(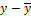 ) ) |
| 50,6 |
6,4 |
-0,9 |
0,81 |
0,5 |
0,25 |
323,84 |
-0,45 |
| 55,4 |
6,0 |
3,9 |
15,21 |
0,1 |
0,01 |
332,4 |
0,39 |
| 60,2 |
6,8 |
8,7 |
75,69 |
0,9 |
0,81 |
409,36 |
7,83 |
| 66,8 |
7,2 |
15,3 |
234,09 |
1,3 |
1,69 |
480,96 |
19,89 |
| 45,9 |
5,6 |
-5,6 |
31,36 |
-0,3 |
0,09 |
257,04 |
1,68 |
| 45,5 |
5,4 |
-6 |
36 |
-0,5 |
0,25 |
245,7 |
3 |
| 70,0 |
8,0 |
18,5 |
342,25 |
2,1 |
4,41 |
560 |
38,85 |
| 30,0 |
4,0 |
-21,5 |
462,25 |
-1,9 |
3,61 |
120 |
40,85 |
| 55,5 |
5,8 |
4 |
16 |
-0,1 |
0,01 |
321,9 |
-0,4 |
| 40,1 |
4,8 |
-11,4 |
129,96 |
-1,1 |
1,21 |
192,48 |
12,54 |
| 45,9 |
5,6 |
-5,6 |
31,36 |
-0,3 |
0,09 |
257,04 |
1,68 |
| 45,5 |
5,4 |
-6 |
36 |
-0,5 |
0,25 |
245,7 |
3 |
| 70,0 |
8,0 |
18,5 |
342,25 |
2,1 |
4,41 |
560 |
38,85 |
| 36,0 |
4,2 |
-15,5 |
240,25 |
-1,7 |
2,89 |
151,2 |
26,35 |
| 55,5 |
5,7 |
4 |
16 |
-0,2 |
0,04 |
316,35 |
-0,8 |
| ∑x=772,9 |
∑y=88,9 |
∑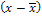 =0,4 =0,4 |
∑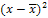 =2009,48 =2009,48 |
∑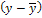 =0,4 =0,4 |
∑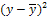 =20,02 =20,02 |
∑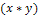 =4773,97 =4773,97 |
∑=193,26 |
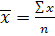 ; ; 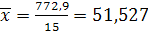 ; ;  ; ;
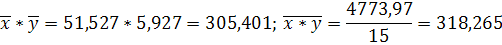
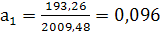 ; ; 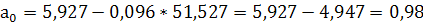
Следовательно, уравнение связи между коэффициентом финансовой независимости и рентабельность капитала имеет вид:
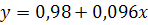
Коэффициент корреляции используется для оценки тесноты связи между исследуемыми показателями.
Для вычисления коэффициента корреляции используется формула:
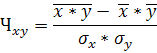
где 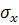 – среднеквадратичное отклонение величины x, – среднеквадратичное отклонение величины x,
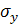 – среднеквадратичное отклонение величины y. – среднеквадратичное отклонение величины y.
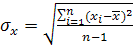 , , 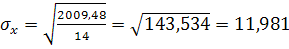 ; ; 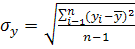 , , 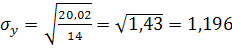
где n – число значений переменных.
Тогда
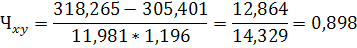
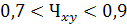
Таким образом, между коэффициентом финансовой независимости и рентабельность капитала связь весьма тесная.
Отобранная для анализа группа данных называется выборной, а вся совокупность данных, из которых выделяется выборка, генеральной совокупностью.
Поскольку значения коэффициента корреляции определяются по выборочным данным и, следовательно, будут различными при рассмотрении различных выборок из одной и той же генеральной совокупности, значение коэффициента корреляции следует рассмотреть как случайную величину.
Таким образом, может возникнуть ситуация, когда величина коэффициента корреляции, рассчитанного по данным выборки, отлична от нуля, а истинный коэффициент корреляции равен нулю.
Для проверки значимости отличия коэффициента корреляции от нуля используется критерий Стьюдента, определяемый по формуле:
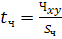 ; ;
где 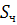 – среднеквадратичная ошибка выборочного коэффициента корреляции: – среднеквадратичная ошибка выборочного коэффициента корреляции:
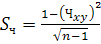 ; ; 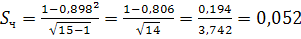 ; ;
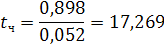
Расчетная величина t-критерия сопоставляется с табличной величиной, отыскиваемой в таблицах значений этого критерия при числе степеней свободы, равном (n-2) и заданной доверительной вероятностью, которая обычно выбирается равной Р = 0,95 или Р = 0,99.
Если расчетная величина t-критерия окажется больше табличной, то это означает, что полученный коэффициент корреляции значимо отличается от нуля; если же расчетное значение критерия меньше табличного, то коэффициент корреляции следует считать равным нулю.
Т.о. 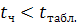 , однако, не следует утверждать, что коэффициент корреляции равен нулю, т.к. это может быть обусловлено случайной выборкой данных. , однако, не следует утверждать, что коэффициент корреляции равен нулю, т.к. это может быть обусловлено случайной выборкой данных.
Величина 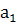 называется коэффициентом регрессии, который является случайной величиной, поэтому возникает необходимость проверки значимости его отличия от нуля. Эта проверка осуществляется с помощью t-критерия. называется коэффициентом регрессии, который является случайной величиной, поэтому возникает необходимость проверки значимости его отличия от нуля. Эта проверка осуществляется с помощью t-критерия.
Проверим значимость коэффициента 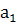 . .
Вычислим ошибку коэффициента регрессии:
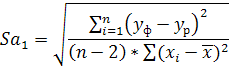
Данные для расчета сведем в таблицу:
| x |
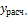 |
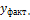 |
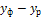 |
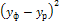 |
| 50,6 |
5,838 |
6,4 |
0,562 |
0,316 |
| 55,4 |
6,298 |
6,0 |
-0,298 |
0,089 |
| 60,2 |
6,759 |
6,8 |
0,041 |
0,002 |
| 66,8 |
7,393 |
7,2 |
-0,193 |
0,037 |
| 45,9 |
5,386 |
5,6 |
0,214 |
0,046 |
| 45,5 |
5,348 |
5,4 |
0,052 |
0,003 |
| 70 |
7,7 |
8,0 |
0,3 |
0,09 |
| 30 |
3,86 |
4,0 |
0,14 |
0,02 |
| 55,5 |
6,308 |
5,8 |
-0,508 |
0,258 |
| 40,1 |
4,83 |
4,8 |
-0,03 |
0,0009 |
| 45,9 |
5,386 |
5,6 |
0,214 |
0,046 |
| 45,5 |
5,348 |
5,4 |
0,052 |
0,003 |
| 70 |
7,7 |
8,0 |
0,3 |
0,9 |
| 36 |
4,436 |
4,2 |
-0,236 |
0,056 |
| 55,5 |
6,308 |
5,7 |
-0,608 |
0,37 |
| ∑=2,237 |
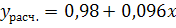
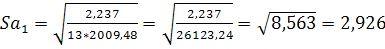 ; ; 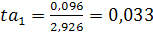
Коэффициент регрессии показывает, на сколько, в среднем, изменяется величина результативного признака у при изменении факторного признака x на единицу.
Таким образом,  , но это может быть обусловлено некоторой погрешностью при выборке данных. , но это может быть обусловлено некоторой погрешностью при выборке данных.
Рассчитаем коэффициент эластичности по формуле:
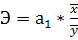 , ,
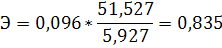
Коэффициент эластичности показывает, на сколько процентов увеличится у при увеличении x на 1%.
Таким образом, произведенный анализ показывает, что рентабельность капитала имеет весьма тесную связь с коэффициентом финансовой независимости (коэффициент корреляции = 0,9) , следовательно, связь прямая.
Из полученного уравнения регрессии следует, что увеличение коэффициента финансовой независимости на 1 % приводит к увеличению рентабельности капитала на 0,835 %.
Задание № 5
Используя данные выборочного наблюдения (таблица 5.1), исследовать уровень выполнения норм выработки рабочими предприятия:
1) С вероятностью до 0,997 определить, в каких пределах будет находиться средний процент выполнения норм выработки всеми рабочими предприятия.
2) С вероятностью до 0,954 определить, в каких пределах будет находиться доля рабочих, не выполняющих нормы выработки, в целом по предприятию.
Необходимо учитывать, что выборка производилась случайным бесповторным способом из 1000 рабочих предприятия.
№
раб.
|
% выполнения норм выработки рабочими, х |
№
раб.
|
% выполнения норм выработки рабочими, х |
№
раб.
|
% выполнения норм выработки рабочими, х |
| 1 |
104 |
11 |
97 |
21 |
94 |
| 2 |
100 |
12 |
125 |
22 |
95 |
| 3 |
103 |
13 |
118 |
23 |
97 |
| 4 |
107 |
14 |
115 |
24 |
99 |
| 5 |
125 |
15 |
96 |
25 |
108 |
| 6 |
126 |
16 |
118 |
26 |
104 |
| 7 |
112 |
17 |
99 |
27 |
104 |
| 8 |
93 |
18 |
100 |
28 |
116 |
| 9 |
95 |
19 |
100 |
29 |
116 |
| 10 |
96 |
20 |
100 |
30 |
109 |
1)
Определяем средний % выполнения норм выработки по выборке:
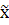 = = 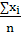 , ,
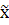 = = 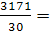 105,7 105,7
Учитывая, что данные получены путем бесповторного механического отбора, определяем среднюю и предельную ошибку выборки с вероятностью до 0,997 по формуле:
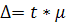
где t – определяется по специальной таблице в зависимости от заданного уровня вероятности (Р) –в данном случае t=3;
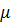 – средняя ошибка выборки. – средняя ошибка выборки.
При бесповторном способе отбора случайной или механической выборки:
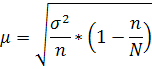
где N – число единиц в генеральной совокупности (N=1000),
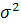 – дисперсия признака; n – число единиц совокупности (n=30) – дисперсия признака; n – число единиц совокупности (n=30)
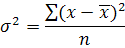
где x – индивидуальные значения признака у каждой единицы совокупности, 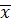 – среднее значение признака. – среднее значение признака.
Расчетная таблица для исчисления дисперсии для нахождения средней квадратичной ошибки выборки:
| № рабочего |
% выполнения норм выработки рабочими |
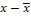 |
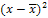 |
| 01 |
104 |
-1,7 |
2,89 |
| 02 |
100 |
- 5,7 |
32,49 |
| 03 |
103 |
- 2,7 |
7,29 |
| 04 |
107 |
1,3 |
1,69 |
| 05 |
125 |
19,3 |
372,49 |
| 06 |
126 |
20,3 |
412,09 |
| 07 |
112 |
6,3 |
39,69 |
| 08 |
93 |
- 12,7 |
161,29 |
| 09 |
95 |
- 10,7 |
114,49 |
| 10 |
96 |
- 9,7 |
94,09 |
| 11 |
97 |
- 8,7 |
75,69 |
| 12 |
125 |
19,3 |
372,49 |
| 13 |
118 |
12,3 |
151,29 |
| 14 |
115 |
9,3 |
86,49 |
| 15 |
96 |
- 9,7 |
94,09 |
| 16 |
118 |
12,3 |
151,29 |
| 17 |
99 |
- 6,7 |
44,89 |
| 18 |
100 |
- 5,7 |
32,49 |
| 19 |
100 |
- 5,7 |
32,49 |
| 20 |
100 |
-5,7 |
32,49 |
| 21 |
94 |
- 11,7 |
136,89 |
| 22 |
95 |
- 10,7 |
114,49 |
| 1 |
2 |
3 |
4 |
| 23 |
97 |
- 8,7 |
75,69 |
| 24 |
99 |
- 6,7 |
44,89 |
| 25 |
108 |
2,3 |
5,29 |
| 26 |
104 |
- 1,7 |
2,89 |
| 27 |
104 |
- 1,7 |
2,89 |
| 28 |
116 |
10,3 |
106,09 |
| 29 |
116 |
10,3 |
106,09 |
| 30 |
109 |
3,3 |
10,89 |
| ∑x=3171 |
∑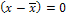 |
∑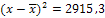 |
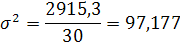
Определяем среднюю квадратическую ошибку бесповторного отбора:
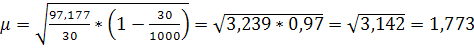
Вычислим предельную ошибку выборки, с вероятностью 0,997 и коэффициентом доверия t=3:
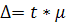 ; ;
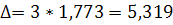 (%) (%)
Таким образом, ошибка наблюдения составляет ±5,319 % из всей совокупности выборки (N=1000).
Доверительный интервал для x будет:
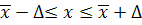 ; ; 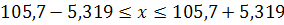 ; ;
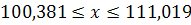
Следовательно, с вероятностью Р = 0,997 можно утверждать, что % выполнения норм выработки на предприятии в отрасли будет заключен в пределах от 100,381 % до 111,019 %.
2) Определяем долю рабочих, не выполняющих норму выработки (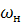 ), т.е. ), т.е. 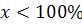 : :
 , ,
где m – количество рабочих, не выполняющих норму выработки,
n – число единиц совокупности (n=30).
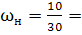 0,3 0,3
Учитывая, что данные получены путем бесповторного отбора, определим среднюю и предельную ошибки выборки с вероятностью Р = 0,954 и t = 2; N=1000
Средняя ошибка:
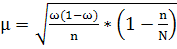 ; ; 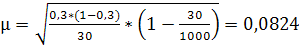 ; ;
Предельная ошибка:
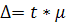 ; ; 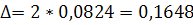 (%) (%)
Определим границы доли рабочих, не выполняющих нормы выработки, в генеральной совокупности:
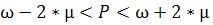 => 0,3 – 0,1648 < P < 0,3 + 0,1648 => 0,3 – 0,1648 < P < 0,3 + 0,1648
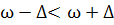 => 0,1352 < P < 0,4648 => 0,1352 < P < 0,4648
Следовательно, с вероятностью 0,954 можно утверждать, что доля рабочих, не выполняющих норму выработки на предприятии будет находиться в пределах 0,1352 ÷ 0,4648.
Задание № 6
Имеются следующие показатели результатов экономической деятельности страны за отчётный год (в действующих ценах, млрд. руб.):
| № п/п |
Показатели |
Сумма |
| 1. |
Валовой выпуск в основных ценах:
– в сфере производства товаров
– в сфере производства услуг
|
17798
12750
|
| 2. |
Промежуточное потребление:
– в сфере производства товаров
– в сфере производства услуг
|
9560
4210
|
| 3. |
Налоги на продукты и импорт |
2602 |
| 4. |
Субсидии на продукты и импорт |
1050 |
| 5. |
Оплата труда наёмных работников |
6725 |
| 6. |
Налоги на производство |
2890 |
| 7. |
Субсидии на производство |
1200 |
| 8. |
Доходы от собственности:
– полученные от «остального мира»
– переданные «остальному миру»
|
2493
1512
|
| 9. |
Текущие трансферты:
– полученные от «остального мира»
– переданные «остальному миру»
|
180
93
|
| 10. |
Расходы на конечное потребление |
10680 |
| 11. |
Капитальные трансферты:
– полученные от «остального мира»
– переданные «остальному миру»
|
5920
17
|
| 12. |
Валовое накопление:
– основного капитала
– материальных оборотных средств
|
4240
560
|
| 13. |
Экспорт товаров и услуг |
6590 |
| 14. |
Импорт товаров и услуг |
1600 |
Постройте «Счёт операций с капиталом» и определите его балансирующую статью (чистое кредитование или чистое заимствование)
Решение задания № 6.
1. Счёт производства:
| Использование |
Ресурсы |
4. Промежуточное потребление
9560 + 4210 = 13770
|
1. Валовой выпуск в основных ценах
17798 + 12750 = 30548
2. Налоги на продукты и импорт 2602
3. Субсидии на продукты и импорт - 1050
|
| 5. ВВП = 1+ 2 + 3 + 4 = 45870
|
| Итого: 32100
|
Итого: 32100
|
2. Счёт образования доходов:
| Использование |
Ресурсы |
3. Оплата труда 6725
4. Налоги на продукты и импорт 2602
|
1. ВВП 32100
2. Субсидии на продукты и импорт 1050
|
| 5. ВПЭ = 1 + 2 – 3 – 4 = 23823
|
| Итого: 33150
|
Итого: 33150
|
3. Счёт первичного распределения доходов:
| Использование |
Ресурсы |
5. Доходы от собственности переданные «остальному миру» 1512
|
1. ВПЭ 23823
2. Доходы от собственности, полученные от «остального мира» 2493
3. Оплата труда 6725
4. Чистые налоги 3242
|
| 6. ВНД = 1 + 2 + 3 + 4 – 5 = 34771
|
| Итого: 36283
|
Итого: 36283
|
4. Счёт вторичного распределения доходов:
| Использование |
Ресурсы |
| 3. Текущие трансферты, переданные «остальному миру» 93
|
1. ВНД 34771
2. Текущие трансферты, полученные от «остального мира» 180
|
| 4. ВНРД = 1 + 2 – 3 = 34858
|
| Итого: 34951
|
Итого: 34951
|
5. Счёт использования доходов:
| Использование |
Ресурсы |
| 2. РКП 10680
|
1. ВНРД 34858
|
| 3. ВНС = 1 – 2 = 24178
|
| Итого: 34858
|
Итого: 34858
|
6. Счёт операций с капиталом:
| Использование |
Ресурсы |
3. Капитальные трансферты, переданные «остальному миру» 17
4. ИЗМОС 560
5. ВНОК 4240
|
1. ВНС 24178
2. Капитальные трансферты, полученные от «остального мира» 5920
|
| 6. ЧК/ЧЗ = 1 + 2 – 3 – 4 – 5 = 25281
|
| Итого: 30098
|
Итого: 30098
|
Балансирующей статьей является чистое кредитование.
|