| Содержание
Введение
Постановка задачи
Проектирование программного модуля
Тестирование программного модуля
Заключение
Список использованных источников
Целью данной курсовой работы является разработка программного модуля для вычисления интеграла 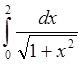 по формуле трапеции и Симпсона с заданной точностью по формуле трапеции и Симпсона с заданной точностью 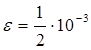 , определяя шаг интегрирования по оценке остаточного члена. Для разработки используется табличный процессор Excel и язык программирования Visual Basic for Application. , определяя шаг интегрирования по оценке остаточного члена. Для разработки используется табличный процессор Excel и язык программирования Visual Basic for Application.
Данная курсовая работа состоит из 4 разделов.
В разделе «Постановка задачи» описаны: математическая модель задачи, входные и выходные данные, обработка ошибок, которые могут быть допущены при работе с данной программой.
В разделе «Проектирование программного модуля» приведена структурная диаграмма программного модуля, схема программного модуля с ее описанием и описан пользовательский интерфейс.
В разделе «Реализация программного модуля» находится код программы с комментариями к нему и описаны используемые операторы и функции.
В разделе «Тестирование программного модуля» показана работа программы.
1.1 Математическая модель задачи
Пусть требуется вычислить интеграл 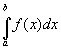 , где f(x) - непрерывная функция. Для простоты рассуждений ограничимся случаем, когда f(x)³ 0. Разобьем отрезок [a, b] на n отрезков точками a=x0
<x1
<x2
<...<xk-1
<xk
<...<xn
=b и с помощью прямых х=хk
построим n прямолинейных трапеций (эти трапеции заштрихованы на рис. 1). Сумма площадей трапеций приближенно равна площади криволинейной трапеции, т.е. , где f(x) - непрерывная функция. Для простоты рассуждений ограничимся случаем, когда f(x)³ 0. Разобьем отрезок [a, b] на n отрезков точками a=x0
<x1
<x2
<...<xk-1
<xk
<...<xn
=b и с помощью прямых х=хk
построим n прямолинейных трапеций (эти трапеции заштрихованы на рис. 1). Сумма площадей трапеций приближенно равна площади криволинейной трапеции, т.е.
Где f(xk-1
) и f(xk
) - соответственно основания трапеций; xk
- xk-1
= (b-a)/n - их высоты.
Таким образом, получена приближенная формула
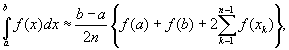
которая и называется формулой трапеций.
Эта формула тем точнее, чем больше n.
Разделим отрезок [a, b] на четное число равных частей n=2m. Площадь криволинейной трапеции соответствующей первым двум отрезкам [x0
x1
] и [x1
x2
] и ограниченной заданной кривой y=f(x) заменим площадью криволинейной трапеции которая ограничена параболой второй степени проходящей через три точки M(x0
y0
) M1
(x1
y1
) M2
(x2
y2
) и имеющей ось параллельную оси Oy. Такую криволинейную трапецию будем называть параболической трапецией.
Уравнение параболы с осью параллельной оси Oy имеет вид
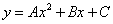
Коэффициенты A, Bи C однозначно определяются из условия что парабола проходит через три заданные точки. Аналогичные параболы строим и для других пар отрезков. Сумма площадей параболических трапеций и даст приближенное значение интеграла.
Вычислим сначала площадь одной параболической трапеции.
Лемма: Если криволинейная трапеция ограничена параболой
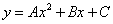
осью Ох и двумя ординатами расстояние между которыми равно 2h то ее площадь равна
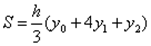 (1)
(1)
где y0
и y2
– крайние ординаты а y1
– ордината кривой в середине отрезка.
Доказательство: Расположим вспомогательную систему координат так как показано на рисунке
Коэффициенты в уравнении параболы 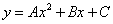 определяются из следующих уравнений:
определяются из следующих уравнений:
Если 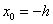 то
то 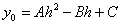
Если 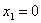 то
то 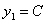 (2)
(2)
Если 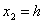 то
то 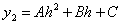
Считая коэффициенты ABC известными определим площадь параболической трапеции с помощью определенного интеграла:
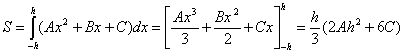
Но из равенства (2) следует что
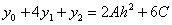 .
.
Следовательно
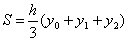
что и требовалось доказать.
Вернемся снова к основной нашей задаче (см. рис). Пользуемся формулой (1) мы можем написать следующие приближенные равенства(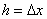 ):
):
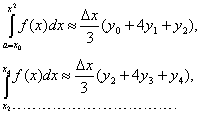
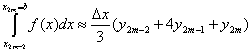
Складывая левые и правые части получим слева искомый интеграл справа его приближенное значение:
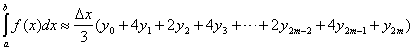
или (3)
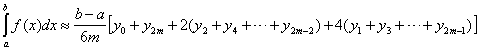
В конечном итоге мы получили формулу Симпсона. Здесь число точек деления 2m произвольно но чем больше это число тем точнее сумма в правой части равенства (3) дает значение интеграла.
1.2 Входные данные
В данном программном модуле входных данных нет. Все необходимые данные изначально заложены в программу.
Выходными данными является значение интеграла 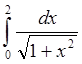 . .
Требования к выходным данным:
1. Все выходные данные выводятся на форму;
2. Ко всем выходным данным запрещен доступ со стороны пользователя.
В данной программе количество ошибок пользователя сведено к минимуму, т. к. пользователь не вводит данные. Все необходимые данные заложены в программу.
2.1 Структурная диаграмма программного модуля
Рисунок 1. Структурная диаграмма программного модуля.
UserForm1 – пользовательская форма.
UserForm_Initialize() – процедура начальной инициализации пользовательской формы.
CommandButton1_Click() – процедура, срабатывающая при нажатии кнопки «Вычислить интеграл», которая производит вычисление и записывает результат.
Simp(a As Double, b As Double) – функция вычисления интеграла по формуле Симпсона.
Trap(a As Double, b As Double) – функция вычисления интеграла по формуле трапеции.
f(x As Double) – функция вычисляющая значение функции 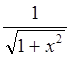 . .
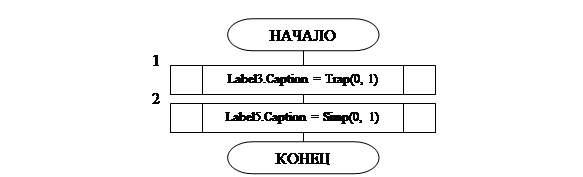
Рисунок 2. Блок схема основной программы.
1 – происходит вызов функции вычисления интеграла методом трапеции.2 – происходит вызов функции вычисления интеграла по формуле Симпсона.
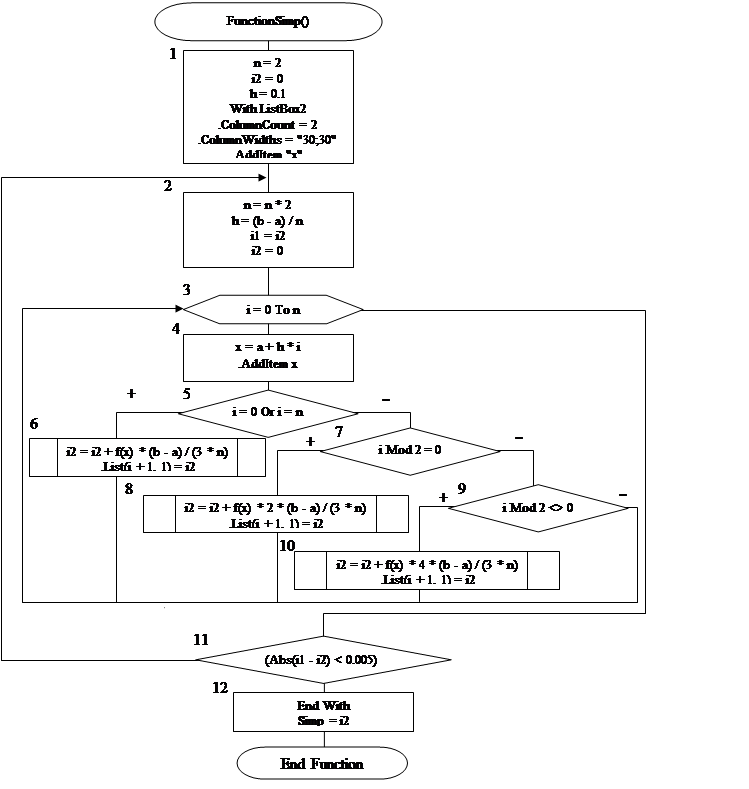
Рисунок 3. Блок схема функции вычисления интеграла по формуле Симпсона.
1 – происходит присвоение переменным начальных значений.
2 – происходит присвоение переменным очередных значений.
3 – описан цикл от 0 до n.
4 – вычисляется аргумент.
5 – проверяется условие.
6 – происходит вычисление интеграла.
7 – проверяется условие.
8 – происходит вычисление интеграла.
9 – проверяется условие.
10 – происходит вычисление интеграла.
11 – проверяется условие.
12 – функции присваивается значение интеграла.
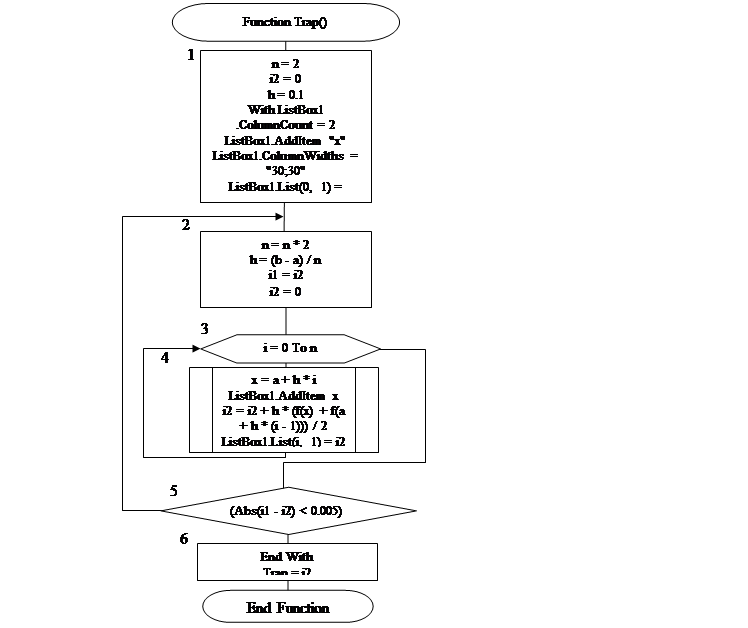
Рисунок 4. Блок схема функции вычисления интеграла по формуле трапеции.
1 – происходит присвоение переменным начальных значений.
2 – происходит присвоение переменным очередных значений.
3 – описан цикл от 0 до n.
4 – вычисляется аргумент и происходит вычисление интеграла.
5 – проверяется условие.
6 – функции присваивается значение интеграла.

Рисунок 5. Блок схема вычисления значения функции.
1 – происходит вычисление значения функции.
2.3 Разработка пользовательского интерфейса
При запуске программы появляется следующее окно:
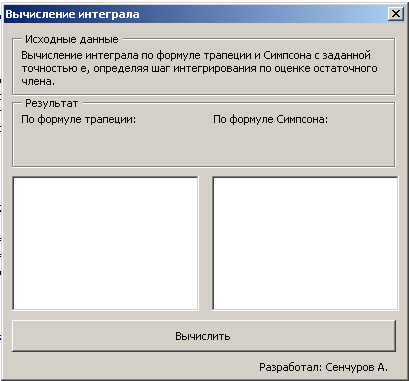
Рисунок 6. Окно программы.
В окне программы расположены исходные данные в элементе управления Label, результат (элемент управления Label), таблицы значений на элементе управления ListBox и кнопка «Вычислить».
3.1 Код программы
Dim n As Integer 'количество делений отрезка
Dim i As Integer 'счетчик итераций
Dim i1 As Double 'переменная для нахождения интеграла
Dim i2 As Double 'переменная для нахождения интеграла
Dim x As Double 'значение аргумента
Dim h As Double 'шаг
Private Sub UserForm_Initialize()
Application.Visible = False 'делаем Excel невидимым
End Sub
Private Sub CommandButton1_Click()
Label3.Caption = Trap(0, 1) 'вычисление интеграла методом трапеции
Label5.Caption = Simp(0, 1) 'вычисление интеграла методом Симпсона
End Sub
Public Function Trap(a As Double, b As Double) As Double ' нахождение интеграла методом трапеции
n = 2
i2 = 0
h = 0.1
With ListBox1
.ColumnCount = 2
ListBox1.AddItem "x"
ListBox1.ColumnWidths = "30;30"
ListBox1.List(0, 1) = "Результат"
Do
n = n * 2
h = (b - a) / n
i1 = i2
i2 = 0
For i = 1 To n
x = a + h * i
ListBox1.AddItem x
i2 = i2 + h * (f(x) + f(a + h * (i - 1))) / 2
ListBox1.List(i, 1) = i2
Next i
Loop While (Abs(i1 - i2) < 0.005)
End With
Trap = i2
End Function
Public Function Simp(a As Double, b As Double) As Double ' нахождение интеграла методом Симпсона
n = 2
i2 = 0
h = 0.1
With ListBox2
.ColumnCount = 2
.ColumnWidths = "30;30"
.AddItem "x"
.List(0, 1) = "Результат"
Do
n = n * 2
h = (b - a) / n
i1 = i2
i2 = 0
For i = 0 To n
x = a + h * i
.AddItem x
If (i = 0 Or i = n) Then
i2 = i2 + f(x) * (b - a) / (3 * n)
.List(i + 1, 1) = i2
Else
If (i Mod 2 = 0) Then
i2 = i2 + f(x) * 2 * (b - a) / (3 * n)
.List(i + 1, 1) = i2
Else
If (i Mod 2 <> 0) Then
i2 = i2 + f(x) * 4 * (b - a) / (3 * n)
.List(i + 1, 1) = i2
End If
End If
End If
Next i
Loop While (Abs(i1 - i2) < 0.005)
End With
Simp = i2
End Function
Public Function f(x As Double) As Double ' нахождение значения функции
f = 1 / Sqr(1 + x ^ 2)
End Function
Private Sub UserForm_QueryClose(Cancel As Integer, CloseMode As Integer) 'Закрытие формы
Select Case MsgBox("Закрыть окно?", vbYesNo + vbQuestion, "Завершение работы")
Case vbYes
Cancel = 0
Application.Quit
Case vbNo
Cancel = -1
End Select
End Sub
3.2 Описание используемых операторов и функций
При разработке программы были использованы следующие операторы и функции:
Оператор присваивания – задает переменной значение другой переменной, выражения или объекта.
Условный оператор (If…Then…Else…End If) – позволяет выбирать и выполнять действия в зависимости от истинности некоторого условия.
Оператор цикла For – позволяет повторять группу операторов заданное число раз.
Цикл с постусловием (Do…Loop While) – используются, когда заранее неизвестно, сколько раз будет выполняться тело цикла, но хотя бы раз тело цикла выполнится.
Функция f(x As Double) – функция, которая вычисляет значение функции в зависимости от аргумента.
Функция Abs(x) – функция, которая возвращает значение аргумента по модулю.
После нажатия на кнопку «Вычислить интеграл» появляется результат.
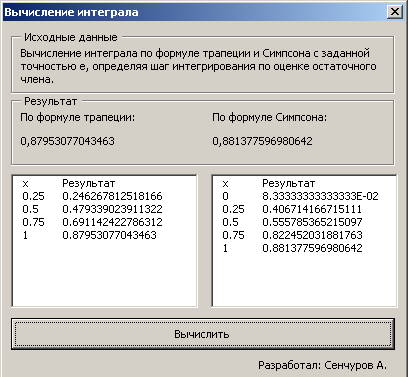
Рисунок 7. Результат выполнения программы.
Целью данной курсовой работы является разработка программного модуля для вычисления интеграла 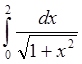 по формуле трапеции и формуле Симпсона с заданной точностью по формуле трапеции и формуле Симпсона с заданной точностью 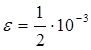 , определяя шаг интегрирования по оценке остаточного члена. Тестирование показало, что результаты, полученные разработанным программным модулем, соответствуют теоретическим расчётам, но расчет по формуле Симпсона оказался точнее. , определяя шаг интегрирования по оценке остаточного члена. Тестирование показало, что результаты, полученные разработанным программным модулем, соответствуют теоретическим расчётам, но расчет по формуле Симпсона оказался точнее.
1. Гарнаев А. Ю. Самоучитель VBA. – СПб: БХВ – Санкт-Петербург, 2002.
2. Гарнаев А. Ю. Разработка приложений. – СПб: БХВ – Санкт-Петербург, 2004.
3. Павловская Т. Учебник по программированию С/С++. – СПб, 2001.
4. Васильев А. VBA в Office 2000: учебный курс – СПб: Питер, 2002.
5. Кузьменков В.Г. VBA 2002. – М.: Издательство БИНОМ, 2002.
|