Курсовая работа
"Абелевы универсальные алгебры"
Содержание
Введение
1. Основные определения, обозначения и используемые результаты
2. Свойства централизаторов конгруэнции универсальных алгебр
3. Формационные свойства нильпотентных алгебр
4. Классы абелевых алгебр и их свойства
Заключение
Список литературы
Введение
Теория формаций алгебраических систем, как самостоятельное направление современной алгебры, начало развиваться сравнительно недавно, в конце 60-х годов прошлого столетия. Отметим, что за последующие четыре десятилетия в таких классических областях исследования, как группы, кольца, алгебры Ли, мультикольца и т.д. формационные методы получили довольно широкое развитие. В теории же универсальных алгебр формационные методы не находят такого широкого применения, что, в первую очередь, связано со сложностью самого объекта исследований. Поэтому получение новых результатов, касающихся формационных свойств универсальных алгебр, представляет несомненный интерес. Именно этой задаче посвящается настоящая курсовая работа. Здесь на основе определения централизатора конгруэнции, введенного Смитом , дается определение абелевои алгебры и доказывается основной результат, что класс всех универсальных абелевых алгебр из мальцевского многообразия образует наследственную формацию. Также рассматривается и свойства абелевых универсальных алгебр.
Перейдем к краткому изложению результатов курсовой работы, которая включает в себя введение, четыре параграфа и список цитируемой литературы из восьми наименований.
 1 является вспомогательным. Здесь приводятся основные определения, обозначения и результаты, используемые в дальнейшем. 1 является вспомогательным. Здесь приводятся основные определения, обозначения и результаты, используемые в дальнейшем.
 2, 3 носят реферативный характер. Здесь подробно с доказательствами на основании результатов работ [1] и [2] излагается теория централизаторов конгруэнции универсальных алгебр и рассматриваются формационные свойства нильпотентных алгебр работы[3]. Сразу же отметим, что все рассматриваемые универсальные алгебры принадлежат фиксированому мальцевскому многообразию. 2, 3 носят реферативный характер. Здесь подробно с доказательствами на основании результатов работ [1] и [2] излагается теория централизаторов конгруэнции универсальных алгебр и рассматриваются формационные свойства нильпотентных алгебр работы[3]. Сразу же отметим, что все рассматриваемые универсальные алгебры принадлежат фиксированому мальцевскому многообразию.
В  4, который является основным, на основании результатов 4, который является основным, на основании результатов  3 вводится понятие абелевой алгебры. Используя методы исследования работы [1] доказывается следующий основной результат: класс всех универсальных абелевых алгебр из мальцевского многообразия образует наследственную формацию. 3 вводится понятие абелевой алгебры. Используя методы исследования работы [1] доказывается следующий основной результат: класс всех универсальных абелевых алгебр из мальцевского многообразия образует наследственную формацию.
1 О
сновные определения, обозначения и используемые результаты
Приведем определения основных понятий, используемых в данной работе из источников [1] и[2]. Для введения понятия алгебы необходимо сначала определить 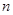 -арные операции. -арные операции.
Определение 1.1.
Если  – непустое множество и – непустое множество и 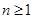 , то , то 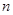 -арной операцией
на множестве -арной операцией
на множестве  назовем отображение прямого произведения назовем отображение прямого произведения 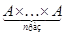 в в  . Рассматриваются и . Рассматриваются и  -арные операции, которые по определению, отмечают некоторый элемент из -арные операции, которые по определению, отмечают некоторый элемент из  . .
Определение 1.2.
Пара 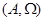 , где , где  – непустое множество, а – непустое множество, а 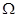 (возможно, пустое) множество операций на (возможно, пустое) множество операций на  , называется универсальной алгеброй
или, короче, алгеброй
. , называется универсальной алгеброй
или, короче, алгеброй
.
Совокупность операций (или опрерационных символов) 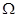 будем называть сигнатурой
. Часто, при введении алгебры, указывают только множество будем называть сигнатурой
. Часто, при введении алгебры, указывают только множество  и не указывают сигнатуру. и не указывают сигнатуру.
Элемент алгебры  отмечаемый отмечаемый  -арной операцией -арной операцией 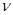 . будем обозначать через . будем обозначать через 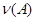 . .
Определение 1.3.
Подмножество 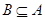 называется подалгеброй
, если называется подалгеброй
, если 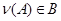 для всякой для всякой  -арной операции -арной операции 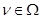 , ,
а если 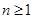 и и 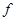 – – 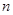 -арная операция из -арная операция из 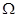 , то , то
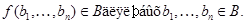
Определение 1.4.
Если 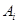 , , 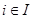 – алгебры сигнатуры – алгебры сигнатуры 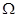 , то прямое произведение , то прямое произведение
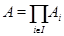
становиться алгеброй той же сигнатуры, если для каждой  -арной операции -арной операции 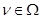 положить положить
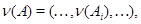
а для 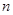 -арной операции -арной операции 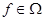 , где , где 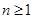 , – , –
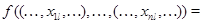
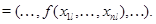
Возникающая таким образом алгебра  называется прямым произведением
алгебр называется прямым произведением
алгебр 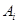 . .
Приведем некоторые определения из
Определение 1.5.
Отображение 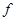 из алгебры из алгебры  в алгебру в алгебру 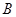 называется гомоморфизмом
, если для любых элементов называется гомоморфизмом
, если для любых элементов 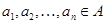 и любой и любой 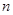 -арной операции -арной операции 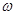 ( (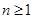 ) справедливо равенство ) справедливо равенство
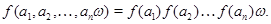
Если же 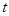 – нульарная операция, то полагаем – нульарная операция, то полагаем
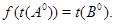
Взаимнооднозначный гомоморфизм алгебры  на на 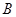 называется изоморфизмом
и обозначается называется изоморфизмом
и обозначается 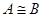 . Гомоморфизм алгебры . Гомоморфизм алгебры  в себя называется эндоморфизмом
алгебры в себя называется эндоморфизмом
алгебры  . Изоморфизм алгебры в себя называется ее автоморфизмом
. . Изоморфизм алгебры в себя называется ее автоморфизмом
.
Определение 1.6.
Конгруэнцией
на алгебре  называется всякая подалгебра называется всякая подалгебра 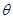 прямого квадрата прямого квадрата 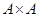 , обладающая следующими свойствами: , обладающая следующими свойствами:
1) (рефлексивность
): 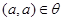 для всех для всех 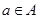 ; ;
2) (симметричность
): если 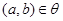 , то , то 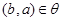 ; ;
3) (транзитивность
): если 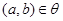 и и 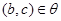 , то , то 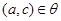 . .
Отметим, что условия 1) – 3) означают, что 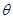 – эквивалентностъ
на множестве – эквивалентностъ
на множестве  . .
Определение 1.7.
Пусть 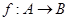 – гомоморфизм алгебры – гомоморфизм алгебры  в в 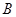 . Ядром гомоморфизма . Ядром гомоморфизма
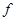 называется подмножество называется подмножество
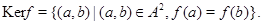
В работе [3] приводятся следующие теоремы об изоморфизмах
Теорема
1
Ядро гомоморфизма является конгруэнцией.
Определение 1.8.
Если 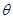 – конгруэнция на алгебре – конгруэнция на алгебре  и и 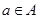 , то множество , то множество
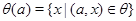
называется классом конгруэнции
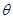 . Множество всех классов конгруэнции . Множество всех классов конгруэнции 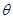 обозначают через обозначают через 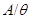 . При этом для каждой . При этом для каждой  -арной операции -арной операции 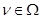 считают считают 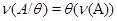 , а для , а для  -арной операции -арной операции  , где , где 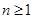 , – , – 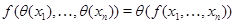 . Получившуюся алгебру называют фактор-алгеброй
алгебры . Получившуюся алгебру называют фактор-алгеброй
алгебры  по конгруэнции по конгруэнции 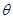 . .
Теорема Первая теорема об изоморфизмах
2
Если 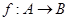 – гомоморфизм алгебры – гомоморфизм алгебры  в в 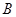 , то , то
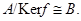
Теорема Вторая теорема об изоморфизмах
3
Пусть 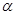 конгруэнция на алгебре конгруэнция на алгебре  , , 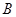 – подалгебра алгебры – подалгебра алгебры  . Тогда . Тогда
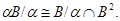
Определение 1.9.
Если 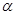 , , 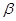 – конгруэнции на алгебре – конгруэнции на алгебре  и и 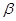 содержится в содержится в 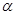 , то обозначим , то обозначим
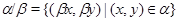
и назовем фактором алгебры  или фактором на
или фактором на  .
.
Теорема Третья теорема об изоморфизмах
4
Пусть 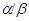 – фактор на алгебре – фактор на алгебре  . Тогда . Тогда
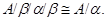
Определение 1.10.
Если 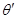 и и 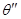 – конгруэнции алгебры – конгруэнции алгебры  , то полагают , то полагают
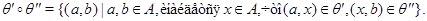
Теорема
5
Произведение двух конгруэнции является конгруэнцией тогда и только тогда, когда они перестановочны.
Определение 1.11.
Класс алгебраических систем 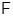 называется формацией
, если выполняются следующие условия: называется формацией
, если выполняются следующие условия:
1) каждый гомоморфный образ любой 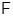 -системы принадлежит -системы принадлежит 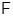 ; ;
2) всякое конечное поддекартово произведение 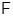 -систем принадлежит -систем принадлежит 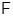 . .
Определение 1.12.
Формальное выражение 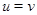 , где , где 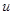 и и 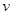 – слова сигнатуры – слова сигнатуры  в счетном алфавите в счетном алфавите 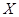 , называется тождеством
сигнатуры , называется тождеством
сигнатуры 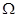 . Скажем, что в алгебре . Скажем, что в алгебре  выполнено тождество выполнено тождество
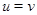 , если после замены букв любыми элементами алгебры , если после замены букв любыми элементами алгебры  и осуществления входящих в слова и осуществления входящих в слова 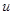 и и 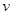 операций слева и справа получается один и тот же элемент алгебры операций слева и справа получается один и тот же элемент алгебры  , т.е. для любых , т.е. для любых 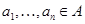 в алгебре в алгебре  имеет место равенство имеет место равенство
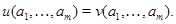
Определение 1.13.
Класс 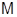 алгебр сигнатуры алгебр сигнатуры 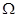 называется многообразием, если существует множество называется многообразием, если существует множество 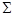 тождеств сигнатуры тождеств сигнатуры 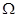 такое, что алгебра сигнатуры такое, что алгебра сигнатуры 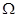 принадлежит классу принадлежит классу 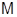 тогда и только тогда, когда в ней выполняются все тождества из множества тогда и только тогда, когда в ней выполняются все тождества из множества 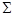 . Многообразие называется мальцевским
, если оно состоит из алгебр, в которых все конгруэнции перестановочны. . Многообразие называется мальцевским
, если оно состоит из алгебр, в которых все конгруэнции перестановочны.
2.
Свойства централизаторов конгруэнции универсальных алгебр
Напомним, что класс 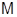 алгебр сигнатуры алгебр сигнатуры 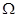 называется многообразием
, если существует множество называется многообразием
, если существует множество 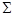 тождеств сигнатуры тождеств сигнатуры 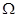 такое, что алгебра сигнатуры такое, что алгебра сигнатуры 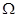 принадлежит классу принадлежит классу 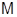 тогда и только тогда, когда в ней выполняются все тождества из множества тогда и только тогда, когда в ней выполняются все тождества из множества 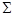 . .
Многообразие называется мальцевским
, если оно состоит из алгебр, в которых все конгруэнции перестановочны.
Все алгебры считаются принадлежащими некоторому фиксированному мальцевcкому многообразию. Используются стандартные обозначения и определения из[2].
В данной работе конгруэнции произвольной алгебры будем обозначать греческими буквами.
Если 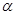 – конгруэнция на алгебре – конгруэнция на алгебре  , то , то
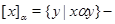
смежный класс алгебры  по конгруэнции по конгруэнции 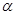 . . 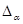 или или 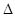 – диагональ алгебры – диагональ алгебры  . .
Для произвольных конгруэнции 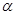 и и 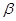 на алгебре на алгебре  будем обозначать будем обозначать 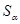 множество всех конгруэнции на алгебре множество всех конгруэнции на алгебре 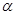 таких, что таких, что
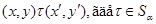
тогда и только тогда, когда
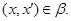
Так как 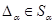 , то множество , то множество 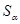 не пусто. не пусто.
Следующее определение дается в работе[2].
Определение 2.1.
Пусть 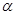 и и 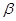 – конгруэнции на алгебре – конгруэнции на алгебре  . Тогда . Тогда 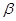 централизует централизует
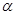 (записывается: (записывается: 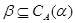 ), если на ), если на 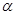 существует такая конгруэнция существует такая конгруэнция 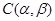 , что: , что:
1) из
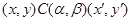
всегда следует
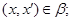
2) для любого элемента
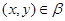
всегда выполняется
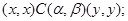
3) если
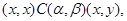
то
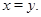
Под термином «алгебра» в дальнейшем будем понимать универсальную алгебру. Все рассматриваемые алгебры предполагаются входящими в фиксированное мальцевское многообразие 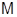 . .
Следующие свойства централизуемости, полученные Смитом[3], сформулируем в виде леммы.
Лемма 2.1.
Пусть 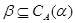 . Тогда: . Тогда:
1) существует единственная конгруэнция 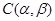 , удовлетворяющая определению 2.1; , удовлетворяющая определению 2.1;
2) 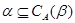 ; ;
3) если
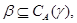
то
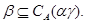
Из леммы 2.1. и леммы Цорна следует, что для произвольной конгруэнции 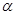 на алгебре на алгебре  всегда существует наибольшая конгруэнция, централизующая всегда существует наибольшая конгруэнция, централизующая 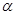 . Она называется централизатором
конгруэнции . Она называется централизатором
конгруэнции 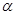 в в  и обозначается и обозначается 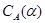 . .
В частности, если 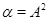 , то централизатор , то централизатор 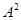 в в  будем обозначать будем обозначать 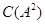 . .
Лемма 2.2.
Пусть 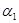 , , 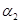 – конгруэнции на алгебре – конгруэнции на алгебре  , , 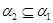 , , 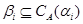 , , 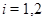 . Тогда справедливы следующие утверждения: . Тогда справедливы следующие утверждения:
1) 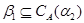 ; ;
2) 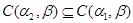 , где , где 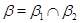 ; ;
3) если выполняется одно из следующих отношений:
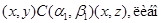
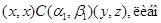
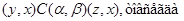
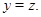
4) из 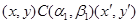 всегда следует всегда следует
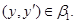
Доказательство:
1) Очевидно, что 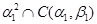 – конгруэнция на – конгруэнция на 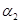 , удовлетворяющая определению 2.1. В силу пункта 1) леммы 2.1. и , удовлетворяющая определению 2.1. В силу пункта 1) леммы 2.1. и 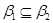 . .
2) 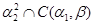 – конгруэнция на – конгруэнция на 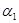 , удовлетворяющая определению 2.1. Значит , удовлетворяющая определению 2.1. Значит
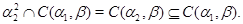
3) Пусть 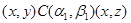 . Тогда . Тогда
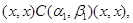
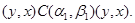
Применим к последним трем соотношениям мальцевский оператор 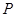 такой, что такой, что
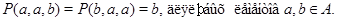
Тогда получим
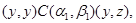
т.е.
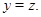
Аналогичным образом показываются остальные случаи из пункта 3).
4) Пусть
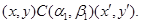
Тогда справедливы следующие соотношения:
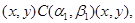
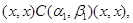
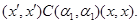
Следовательно,
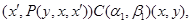
где 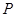 – мальцевский оператор. – мальцевский оператор.
Тогда
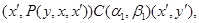
то есть 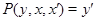 . .
Так как
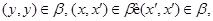
то 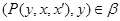 . .
Таким образом 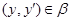 . Лемма доказана. . Лемма доказана.
Следующий результат оказывается полезным при доказательстве последующих результатов.
Лемма. 2.3.
Любая подалгебра алгебры 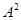 , содержащая диагональ , содержащая диагональ 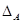 , является конгруэнцией на алгебре , является конгруэнцией на алгебре  . .
Доказательство:
Пусть
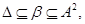
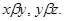
Тогда из
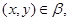
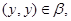
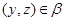
следует, что
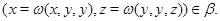
Аналогичным образом из
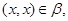
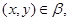
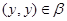
получаем, что
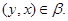
Итак, 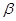 симметрично и транзитивно. Лемма доказана. симметрично и транзитивно. Лемма доказана.
Доказательство следующего результата работы [1] содержит пробел, поэтому докажем его.
Лемма 2.4.
Пусть 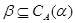 . Тогда . Тогда 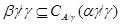 для любой конгруэнции для любой конгруэнции 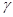 на алгебре на алгебре  . .
Доказательство:
Обозначим 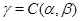 и определим на алгебре и определим на алгебре 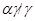 бинарное отношение бинарное отношение 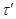 следующим образом: следующим образом:
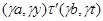
тогда и только тогда, когда
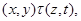
где
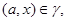
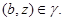
Используя лемму 2.3, нетрудно показать, что 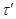 – конгруэнция на алгебре – конгруэнция на алгебре 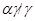 , причем , причем
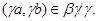
Пусть
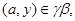
то есть
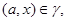
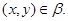
Тогда
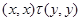
и, значит
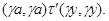
Пусть, наконец, имеет место
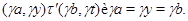
Тогда справедливы следующие соотношения:
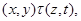
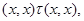
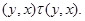
применяя мальцевчкий оператор 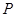 к этим трем соотношениям, получаем к этим трем соотношениям, получаем
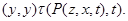
Из леммы 2.2 следует, что
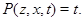
Так как
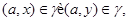
то
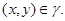
Значит,
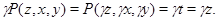
Но 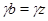 , следовательно, , следовательно, 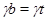 . .
Итак,
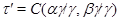
и удовлетворяет определению 2.1. Лемма доказана.
Лемма 2.5.
Пусть 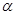 , , 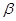 – конгруэнции на алгебре – конгруэнции на алгебре  , , 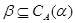 и и 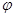 – изоморфизм, определенный на – изоморфизм, определенный на  . .
Тогда для любого элемента 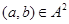 отображение отображение 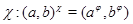 определяет изоморфизм алгебры определяет изоморфизм алгебры 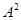 на алгебру на алгебру 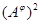 , при котором , при котором 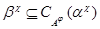 . .
В частности, 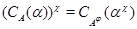 . .
Доказательство.
Очевидно, что 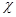 – изоморфизм алгебры – изоморфизм алгебры 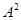 на алгебру на алгебру 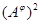 , при котором конгруэнции , при котором конгруэнции 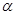 , , 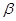 изоморфны соответственно конгруэнциям изоморфны соответственно конгруэнциям 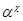 и и 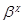 . .
Так как
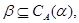
то определена конгруэнция
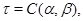
удовлетворяющая определению 2.1.
Изоморфизм 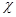 алгебры алгебры 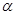 на алгебру на алгебру 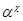 индуцирует в свою очередь изоморфизм индуцирует в свою очередь изоморфизм 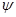 алгебры алгебры 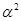 на алгебру на алгебру 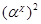 такой, что такой, что
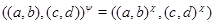
для любых элементов 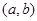 и и 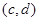 , принадлежащих , принадлежащих 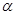 . Но тогда легко проверить, что . Но тогда легко проверить, что 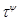 – конгруэнция на алгебре – конгруэнция на алгебре 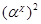 , изоморфная конгруэнции , изоморфная конгруэнции 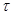 . .
Это и означает, что
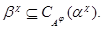
Лемма доказана.
Определение 2.2.
Если 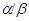 и и 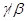 – факторы на алгебре – факторы на алгебре  такие, что такие, что
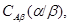
то конгруэнцию 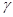 обозначим через обозначим через 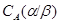 и назовем централизатором фактора и назовем централизатором фактора
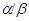 в в  . .
Напомним, что факторы 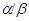 и и 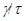 назыавются перспективными
, если либо назыавются перспективными
, если либо
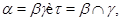
либо
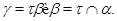
Докажем основные свойства централизаторов конгруэнции.
Теорема
6
Пусть 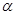 , , 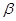 , , 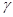 , , 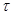 – конгруэнции на алгебре – конгруэнции на алгебре  . Тогда: . Тогда:
1) если 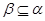 , то , то
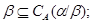
2) если 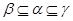 , то , то
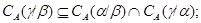
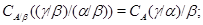
3) если 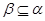 , , 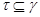 и факторы и факторы 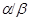 , , 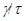 перспективны, то перспективны, то
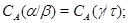
4) если 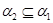 – конгруэнции на – конгруэнции на  и и 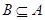 , то , то
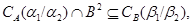
где 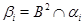 , , 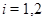 . .
Доказательство.
1) Так как конгруэнция 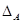 централизует любую конгруэнцию и централизует любую конгруэнцию и 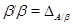 , то , то
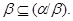
2) Из первого пункта лемы 2.2 следует, что
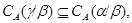
а в силу леммы 2.4 получаем, что
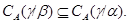
Пусть 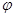 – изоморфизм – изоморфизм 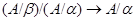 . Обозначим . Обозначим
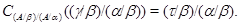
По лемме 2.5 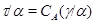 , а по определению , а по определению
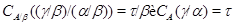
Следовательно,
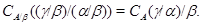
3) Очевидно, достаточно показать, что для любых двух конгруэнции 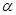 и и 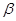 на алгебре на алгебре 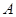 имеет место равенство имеет место равенство

Покажем вналале, что
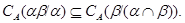
Обозначим 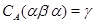 . Тогда, согласно определению 2.1. на алгебре . Тогда, согласно определению 2.1. на алгебре 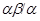 существует такая конгруэнция существует такая конгруэнция 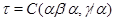 , что выполняются следующие свойства: , что выполняются следующие свойства:
а) если 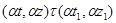 , то , то
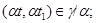
б) для любого элемента 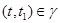 , ,
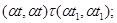
в) если
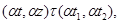
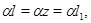
то
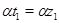
Построим бинарное отношение 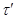 на алгебре на алгебре 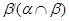 следующим образом: следующим образом:
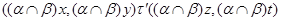
тогда и только тогда, когда
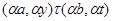
и
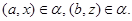
Покажем, что 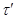 – конгруэнция на – конгруэнция на 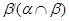 . Пусть . Пусть
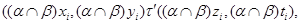
для 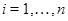 . Тогда . Тогда
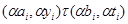
и
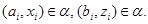
Так как 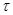 – конгруэнция, то для любой – конгруэнция, то для любой 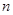 -арной операции -арной операции  имеем имеем
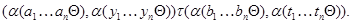
Очевидно, что
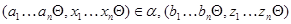
и
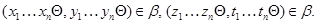
Следовательно,
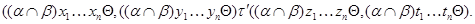
Очевидно, что для любой пары 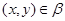
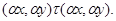
Значит,
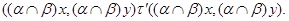
Итак, по лемме 2.3, 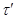 – конгруэнция на – конгруэнция на 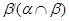 . Покажем теперь, что . Покажем теперь, что 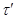 удовлетворяет определению 2.1, то есть удовлетворяет определению 2.1, то есть 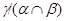 централизует централизует 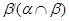 . Пусть . Пусть
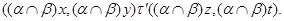
Тогда
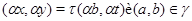
Так как 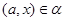 , ,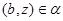 и и 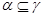 , то , то 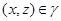 . Следовательно, . Следовательно, 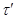 удовлетворяет определению 2.1. удовлетворяет определению 2.1.
Если 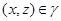 , то , то
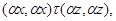
значит,
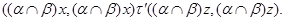
Пусть, наконец, имеет место (1) и
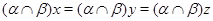
Тогда 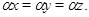
Так как 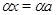 и и 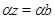 , то , то 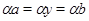 , следовательно, , следовательно, 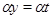 . Из (2) следует, что . Из (2) следует, что 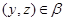 , а по условию , а по условию 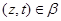 . Значит, . Значит, 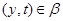 и поэтому и поэтому
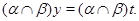
Тем самым показано, что конгруэнция 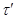 удовлетворяет определению 2.1, то есть удовлетворяет определению 2.1, то есть 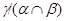 централизует централизует 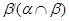 . .
Докажем обратное включение. Пусть
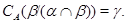
Тогда на алгебре 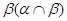 определена конгруэнция определена конгруэнция
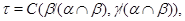
удовлетворяющая определению 2.1. Построим бинарное отношение 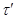 на алгебре на алгебре 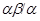 следующим образом: следующим образом:
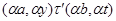
тогда и только тогда, когда
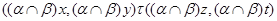
и 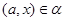 , , 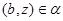 . .
Аналогично, как и выше, нетрудно показать, что 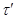 – конгруэнция на алгебре – конгруэнция на алгебре 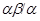 . Заметим, что из доказанного включения в одну сторону следует, что . Заметим, что из доказанного включения в одну сторону следует, что 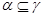 . Покажем поэтому, что . Покажем поэтому, что 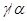 централизует централизует 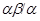 . .
Так как
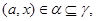
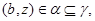
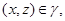
то
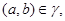
то есть 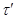 удовлетворяет условию 1) определения 2.1. удовлетворяет условию 1) определения 2.1.
Если 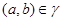 , то , то
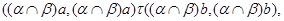
следовательно,
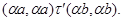
Пусть имеет место (3) и 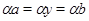 . .
Так как
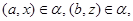
то
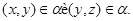
Из (4) следует, что 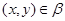 , следовательно, , следовательно,
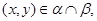
то есть
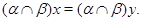
На основании леммы 2.2 заключаем, что
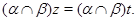
Следовательно, 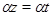 . .
А так как 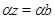 , то , то 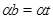 , то есть , то есть
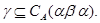
4) Обозначим 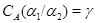 . Пусть . Пусть
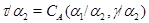
и удовлоетворяет определению 2.1.
Определим бинарное отношение 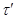 на на 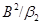 следующим образом следующим образом
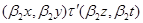
тогда и только тогда, когда
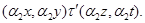
Аналогично, как и выше, нетрудно показать, что 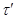 – конгруэнция, удовлетворяющая определению 2.1. – конгруэнция, удовлетворяющая определению 2.1.
Это и означает, что
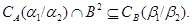
Теорема доказана.
Как следствия, из доказанной теоремы получаем аналогичные свойства централизаторов в группах и мультикольцах.
3. Формационные свойства нильпотентных алгебр
Как уже отмечалось, все алгебры считаются принадлежащими некоторому фиксированному мальцевскому многообразию и используются стандартные обозначения и определения из[1].
Напомним, что для 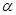 и и 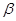 – конгруэнции на алгебре – конгруэнции на алгебре 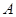 – говорят, что – говорят, что 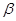 централизует централизует
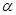 (записывается: (записывается: 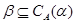 ), если на ), если на 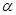 существует такая конгруэнция существует такая конгруэнция 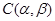 , что: , что:
1) из 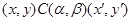 всегда следует всегда следует
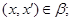
2) для любого элемента 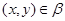 всегда выполняется всегда выполняется
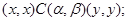
3) если 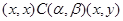 , то , то
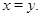
Очевидно, что для любой конгруэнции 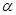 на алгебре на алгебре 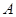 конгруэнция конгруэнция 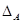 централизует централизует 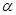 . В этом случае . В этом случае 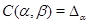 . .
Заметим, что если 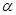 и и 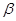 – конгруэнции на группе – конгруэнции на группе 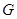 и и 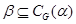 , то для нормальных подгрупп , то для нормальных подгрупп 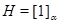 и и 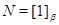 группы группы 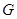 и любых элементов и любых элементов 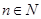 , , 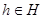 имеют место следующие соотношения: имеют место следующие соотношения:
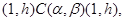
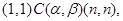
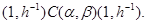
Тогда
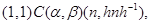
и в силу транзитивности 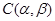 из этих соотношений следует, что из этих соотношений следует, что
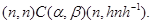
По определению 2.1 получаем, что
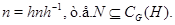
Следующее определение центральности принадлежит Смиту .
Определение 3.1.
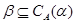 , если существует такая , если существует такая 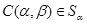 , что для любого , что для любого 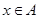 , ,
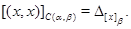
Докажем, что определение 2.1. эквивалентно определению 3.1. 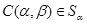 означает условие 1) из определения 2.1. И наоборот, условие 1) означает, что означает условие 1) из определения 2.1. И наоборот, условие 1) означает, что 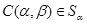 . .
Пусть 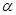 и и 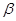 – конгруэнции, удовлетворяющие определению 2.1. Из условия 2) следует, что для любого элемента – конгруэнции, удовлетворяющие определению 2.1. Из условия 2) следует, что для любого элемента 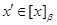 , ,
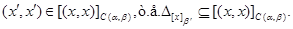
Докажем обратное включение.
Пусть 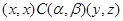 . Так как . Так как 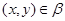 , то из условия 2) следует, что , то из условия 2) следует, что
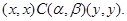
В силу транзитивности 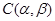 имеем имеем
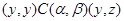
и, значит, в силу условия 3) 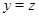 . Итак . Итак
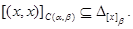
Покажем, что из определения 3.1. следуют условия 2) и 3) определения 2.1. Если 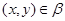 , то , то
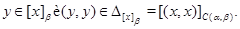
Это означает 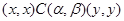 . .
Для 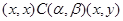 получаем, что получаем, что
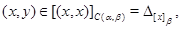
откуда 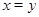 . .
Согласно работе
Определение 3.2.
Алгебра 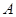 называется нильпотентной
, если существует такой ряд конгруэнции называется нильпотентной
, если существует такой ряд конгруэнции
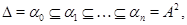
называемый центральным
, что
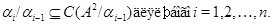
Лемма 3.1.
Любая подалгебра нильпотентной алгебры нильпотентна.
Доказательство:
Пусть 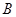 – подалгебра нильпотентной алгебры – подалгебра нильпотентной алгебры 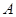 . Так как . Так как 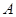 обладает центральным рядом обладает центральным рядом
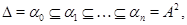
то для любого 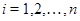 на алгебре на алгебре 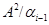 существует конгруэнция существует конгруэнция 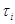 удовлетворяющая определению 2.1. А именно, из удовлетворяющая определению 2.1. А именно, из
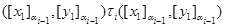
всегда следует
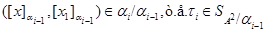
и
1) для любого элемента
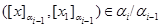
всегда выполняется
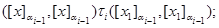
2) если
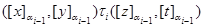
и
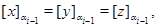
то
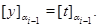
Заметим, что в дальнейшем, для сокращения записи, будем учитывать тот факт, что
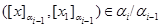
тогда и только тогда, когда
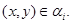
Построим следующий ряд конгруэнции на алгебре 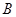 : :
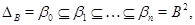
где
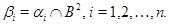
Покажем, что этот ряд является центральным. Для этого на алгебре 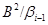 для любого для любого 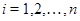 определим бинарное отношение определим бинарное отношение 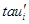 следующим образом: следующим образом:
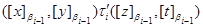
тогда и только тогда, когда
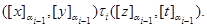
Покажем, что 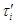 – конгруэнция на алгебре – конгруэнция на алгебре 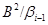 . Пусть . Пусть
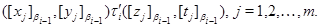
Тогда
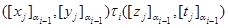
и для любой 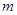 -арной операции -арной операции 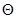 имеем имеем
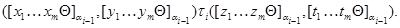
Следовательно,
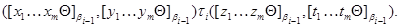
Итак, 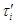 – подалгебра алгебры – подалгебра алгебры 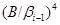 . .
Очевидно, что для любого элемента 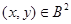 имеет место имеет место
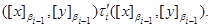
Таким образом, согласно лемме 2.3, 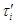 – конгруэнция на алгебре – конгруэнция на алгебре 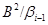 . .
Пусть
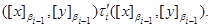
Тогда 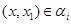 и так как и так как 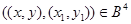 , то , то
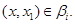
Если 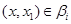 , то , то 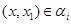 и, значит, и, значит,
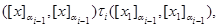
т.е.
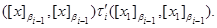
Пусть, наконец,
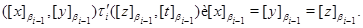
Тогда
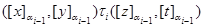
и так как
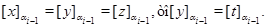
Следовательно,
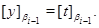
Итак, конгруэнция 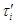 удовлетворяет определению 2.1. для любого удовлетворяет определению 2.1. для любого 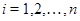 . Лемма доказана. . Лемма доказана.
Лемма 3.2.
Пусть 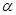 и и 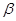 – конгруэнции на алгебре – конгруэнции на алгебре 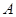 , ,
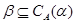
и 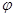 – изоморфизм, определенный на алгебре – изоморфизм, определенный на алгебре 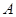 . .
Тогда для любого элемента 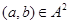 отображение отображение
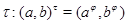
определяет изоморфизм алгебры 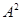 на алгебру на алгебру 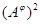 , при котором , при котором
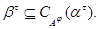
Доказательство:
Очевидно, что 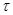 – изоморфизм алгебры – изоморфизм алгебры 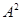 на алгебру на алгебру 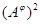 , при котором конгруэнции , при котором конгруэнции 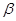 и и 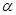 изоморфны соответственно конгруэнциям изоморфны соответственно конгруэнциям 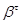 и и 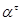 . .
Так как 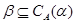 , то существует конгруэнция , то существует конгруэнция 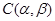 на алгебре на алгебре 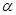 , удовлетворяющая определению 2.1. Изоморфизм , удовлетворяющая определению 2.1. Изоморфизм 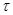 алебры алебры 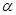 на алгебру на алгебру 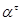 индуцирует в свою очередь изоморфизм индуцирует в свою очередь изоморфизм 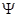 алгебры алгебры 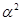 на алгебру на алгебру 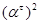 такой, что такой, что
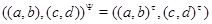
для любых элементов 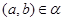 , , 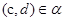 . .
Но тогда легко проверить, что 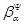 – конгруэнция на алгебре – конгруэнция на алгебре 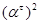 изоморфная конгруэнции изоморфная конгруэнции 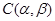 . Это и означает, что . Это и означает, что
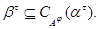
Лемма доказана.
Лемма 3.3.
Фактор-алгебра нильпотентной алгебры нильпотентна.
Доказательство:
Пусть
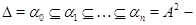
центральный ряд алгебры 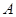 . Покажем, что для любой конгруэнции . Покажем, что для любой конгруэнции 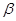 на алгебре на алгебре 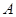 ряд ряд
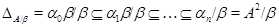
является центральным, т.е.
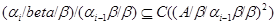
для любого 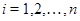 . В силу известных теорем об изоморфизмах для алгебр (см., например, теоремы II.3.7, II.3.11 ) и леммы 3.2., достаточно показать, что . В силу известных теорем об изоморфизмах для алгебр (см., например, теоремы II.3.7, II.3.11 ) и леммы 3.2., достаточно показать, что
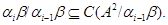
Пусть 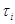 – конгруэнция на алгебре – конгруэнция на алгебре 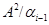 , удовлетворяющая определению 2.1. Определим бинарное отношение , удовлетворяющая определению 2.1. Определим бинарное отношение 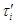 на алгебре на алгебре 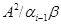 следующим образом следующим образом
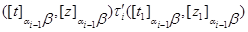
тогда и только тогда, когда найдутся такие элементы 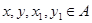 , что , что
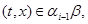
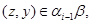
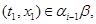
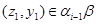
и
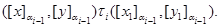
Непосредственной проверкой убеждаемся, что 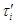 – конгруэнция на алгебре – конгруэнция на алгебре 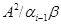 . .
Таким образом осталось показать, что 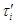 удовлетворяет определению 2.1. удовлетворяет определению 2.1.
Пусть
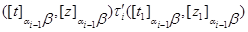
тогда из соотношения
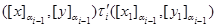
следует, что
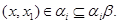
Так как
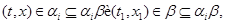
то 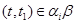 . Итак, . Итак,
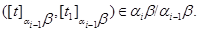
Пусть 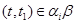 . Тогда для некоторого элемента . Тогда для некоторого элемента 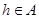 , , 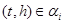 и и 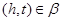 . .
Таким образом,
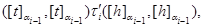
следовательно,
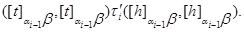
Так как 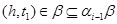 , то это означает, что , то это означает, что
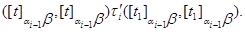
Пусть
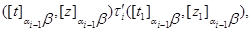
где
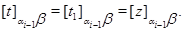
Покажем, что 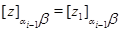 . В силу определения . В силу определения 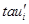 найдутся найдутся 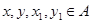 , что , что
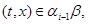
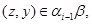
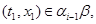
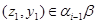
и
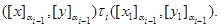
При этом имеют место следующие соотношения:
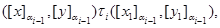
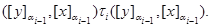
Следовательно,
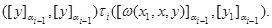
Но тогда по определению 3.2.
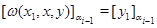
А так как 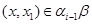 , то , то
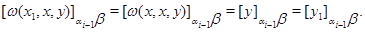
Теперь из того, что
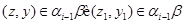
следует, что
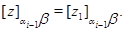
Лемма доказана.
Доказательство следующего результата осуществляется простой проверкой.
Лемма 3.4.
Пусть 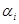 – конгруэнция на алгебре – конгруэнция на алгебре 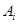 , , 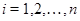 . Пологая . Пологая
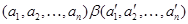
тогда и только тогда, когда 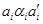 для любого для любого 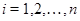 , получаем конгруэнцию , получаем конгруэнцию 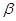 на алгебре на алгебре 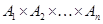 . .
Лемма 3.5.
Прямое произведение конечного числа нильпотентных алгебр нильпотентно.
Доказательство:
Очевидно, достаточно показать, что если 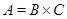 , , 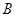 и и 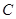 – нильпотентные алгебры, то – нильпотентные алгебры, то  – нильпотентная алгебра. – нильпотентная алгебра.
Пусть
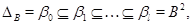
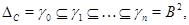
центральные ряды алгебр 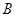 и и 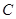 соответственно. Если соответственно. Если 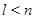 , то, уплотнив первый ряд повторяющимися членами, получим центральный ряд алгебры , то, уплотнив первый ряд повторяющимися членами, получим центральный ряд алгебры 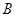 длины длины 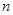 . Таким образом, можно считать, что эти ряды имеют одинаковую длину, равную . Таким образом, можно считать, что эти ряды имеют одинаковую длину, равную 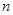 . .
Построим теперь ряд конгруэнции на алгебре  следующим образом: следующим образом:
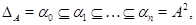
где 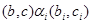 тогда и только тогда, когда тогда и только тогда, когда 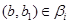 , , 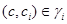 , , 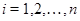 . .
Покажем, что последний ряд является центральным, т.е. 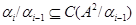 для произвольного для произвольного 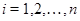 . Так как . Так как
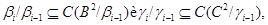
то на алгебрах 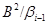 и и 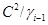 соответственно заданы конгруэнци соответственно заданы конгруэнци 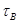 и и 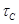 , удовлетворяющие определению 2.1. , удовлетворяющие определению 2.1.
Определим бинарное отношение 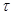 на алгебре на алгебре 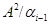 следующим образом: следующим образом:
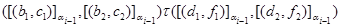
и только тогда, когда
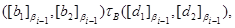
и
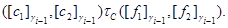
Легко непосредственной проверкой убедиться, что 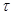 – конгруэнция на алгебре – конгруэнция на алгебре 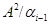 . Осталось показать, что . Осталось показать, что 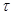 удовлетворяет определению 2.1. удовлетворяет определению 2.1.
Пусть имеет место
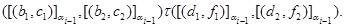
Тогда согласно введенному определению 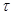
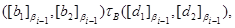
и
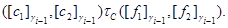
откуда следует, что
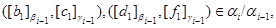
т.е.
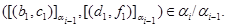
Пусть
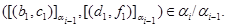
Это означает
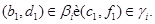
Но тогда
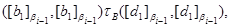
и
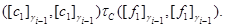
Следовательно,
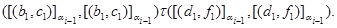
Пусть имеет место
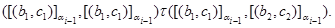
Это означает, что
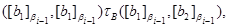
и
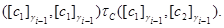
Значит, 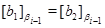 и и 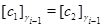 , т.е. , т.е. 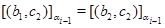 . Лемма, доказана. . Лемма, доказана.
Как известно, наследственной формацией называется класс алгебр, замкнутых относительно фактор-алгебр, подпрямых произведений и относительно подалгебр.
Результаты, полученные в леммах 3.1, 3.3, 3.5 можно сформулировать в виде следующей теоремы.
Теорема
7
Класс всех нильпотентных алгебр мальцевского многообразия является наследственной формацией.
Определение 3.3.
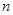 -арная группа -арная группа 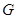 называется нильпотентной
, если она обладает таким нормальным рядом называется нильпотентной
, если она обладает таким нормальным рядом
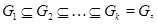
что
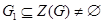
и
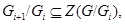
для любого 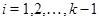 . .
Так как конгруэнции на 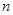 -арных группах попарно перестановочны (смотри, например, ), то это дает возможность использовать полученные результаты в исследовании таких групп. -арных группах попарно перестановочны (смотри, например, ), то это дает возможность использовать полученные результаты в исследовании таких групп.
Лемма 3.6.
Пусть 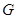 – – 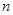 -арная группа. -арная группа.  и и 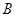 – нормальные подгруппы группы – нормальные подгруппы группы 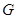 и и 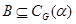 . .
Тогда 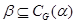 , где , где 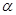 и и 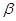 конгруэнции, индуцированные соответственно подгруппами конгруэнции, индуцированные соответственно подгруппами  и и 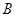 на группе на группе 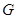 . .
Доказательство:
Подгруппы  и и 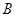 индуцируют на группе индуцируют на группе 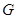 конгруэнции конгруэнции 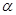 и и 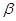 , определяемые следующим образом: , определяемые следующим образом:
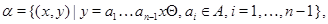
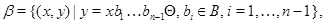
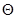 – – 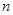 -арная операция. -арная операция.
Определим на 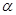 бинарное отношение бинарное отношение 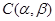 следующим образом: следующим образом:
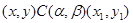
тогда и только тогда, когда существуют такие последовательности элементов 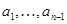 и и 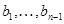 из из  и и 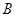 соответственно, что соответственно, что
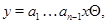
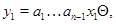
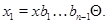
Покажем, что 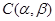 – подалгебра алгебры – подалгебра алгебры 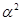 . Для сокращения записи будем в дальнейшем опускать . Для сокращения записи будем в дальнейшем опускать 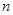 -арный оператор -арный оператор  . .
Пусть
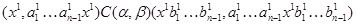
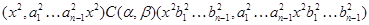
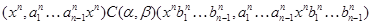
Так как  , то , то
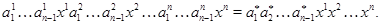
Так как 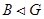 , то , то
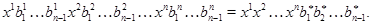
Поэтому в силу того, что 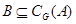 , ,
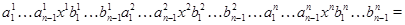
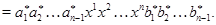
Итак, 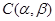 – подалгебра алгебры – подалгебра алгебры 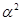 . .
Пусть 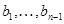 – нейтральная последовательность группы – нейтральная последовательность группы 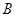 , а, следовательно, и группы , а, следовательно, и группы 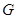 . Тогда из определения бинарного отношения . Тогда из определения бинарного отношения 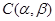 следует, что следует, что
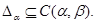
Тем самым доказало, что 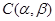 – конгруэнция на – конгруэнция на 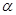 . .
Тo, что 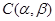 удовлетворяет определению 2.1, очевидно. Лемма доказана. удовлетворяет определению 2.1, очевидно. Лемма доказана.
Лемма 3.7.
Пусть 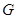 – нильпотентная – нильпотентная 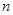 -арная группа. Тогда -арная группа. Тогда 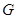 удовлетворяет определению 2.1. удовлетворяет определению 2.1.
Доказательство:
Так как 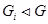 для любого для любого 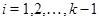 , то , то 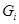 индуцирует конгруэнцию индуцирует конгруэнцию 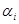 на на 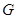 . Таким образом . Таким образом 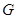 обладает рядом конгруэнции, который в силу леммы 3.6 будет являться центральным. Лемма доказана. обладает рядом конгруэнции, который в силу леммы 3.6 будет являться центральным. Лемма доказана.
В частности, для произвольной бинарной группы 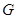 отсюда следует, что отсюда следует, что 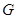 нильпотентна тогда и только тогда, когда, нильпотентна тогда и только тогда, когда, 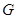 удовлетворяет определению 3.2. В этом случае теорема 3.2 просто констатируе тот факт, что класс всех нильпотентных групп образует наследственную формацию. удовлетворяет определению 3.2. В этом случае теорема 3.2 просто констатируе тот факт, что класс всех нильпотентных групп образует наследственную формацию.
4. Классы абелевых алгебр и их свойства
Как уже было отмечено в параграфе 3, алгебра  называется нильпотентной
, если существует такой ряд конгруэнций называется нильпотентной
, если существует такой ряд конгруэнций
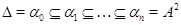
называемый центральным, что
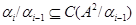
для любого 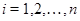 . .
Определение 4.1.
В случае, если для нильпотентной алгебры  в центральном ряде в центральном ряде 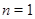 , то есть если для нее , то есть если для нее 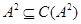 , то алгебра , то алгебра  называется, абелевой
. называется, абелевой
.
Лемма 4.1.
Любая подалгебра абелевой алгебры абелева.
Доказательство:
Пусть 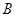 подалгебра абелевой алгебры подалгебра абелевой алгебры  . .
Так как по определению 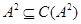 , то на , то на 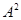 существует такая конгруэнция существует такая конгруэнция 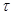 , что: , что:
1) из
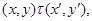
всегда следует
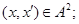
2) для любого элемента
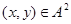
всегда выполняется
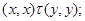
3) если
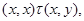
то
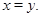
Рассмотрим конгруэнцию
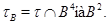
Действительно, если
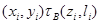
для 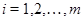 , то , то
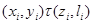
и для любой 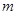 -арной опеации -арной опеации 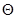 имеем имеем
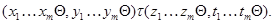
Но поскольку 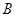 подалгебра алгебры подалгебра алгебры  , получаем , получаем
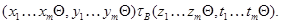
Значит, 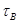 подалгебра алгебры подалгебра алгебры 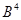 . .
Очевидно, что для любого элемента 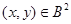 имеет место имеет место
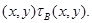
Таким образом, 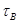 конгруэнция ня алгебре конгруэнция ня алгебре 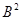 . .
Пусть
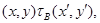
тогда
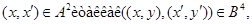
то 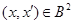 Если Если 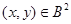 , то , то
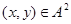
и, значит,
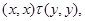
т.е.
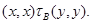
Пусть, наконец,
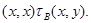
Тогда
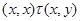
и значит 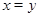 . .
Итак, конгруэнция 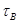 удовлетворяет определению 2.1. Лемма доказана. удовлетворяет определению 2.1. Лемма доказана.
Лемма 4.2.
Фактор-алгебра абелевой алгебры абелева.
Доказательство:
Пусть алгебра  – абелева, то есть – абелева, то есть 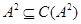 . Покажем, что для любой конгруэнции . Покажем, что для любой конгруэнции 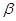 на на  выполняется выполняется
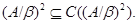
Пусть 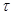 – конгруэнция на алгебре – конгруэнция на алгебре 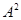 , удовлетворяющая определению 2.1. , удовлетворяющая определению 2.1.
Определим бинарное отношение 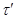 на алгебре на алгебре 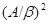 следующим образом: следующим образом:
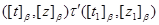
тогда и только тогда, когда найдуться такие элементы  , , 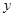 , , 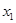 , , 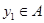 , что , что
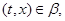
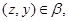
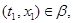
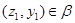
и
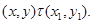
Непосредственной проверкой убеждаемся, что 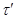 – конгруэнция на алгебре – конгруэнция на алгебре 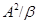 . .
Таким образом осталось показать, что 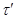 удовлетворяет определению 2.1. Пусть удовлетворяет определению 2.1. Пусть
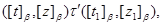
тогда
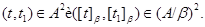
Пусть
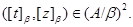
Тогда 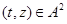 , и по определению 2.1 , и по определению 2.1
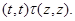
При этом 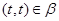 и и 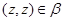 . Согласно нашим обозначениям получаем, что . Согласно нашим обозначениям получаем, что
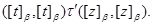
Пусть
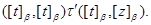
Тогда найдутся 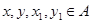 , что , что
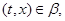
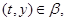
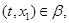
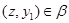
и
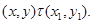
При этом
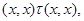
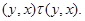
Следовательно,
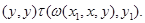
Но тогда по определению 3.1. 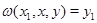 . А так как . А так как 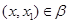 , то , то
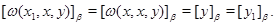
Теперь из того, что
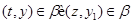
следует, что
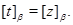
Лемма доказана.
Лемма 4.3.
Прямое произведение конечного числа абелевых алгебр абелево.
Доказательство:
Очевидно, достаточно показать, что если 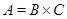 , , 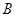 и и 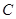 – абелевы алгебры, то – абелевы алгебры, то  – абелева алгебра. – абелева алгебра.
Пусть 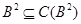 и и 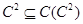 . Это означает, что на алгебрах . Это означает, что на алгебрах 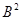 и и 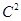 заданы cоответсвенно конгруэнции заданы cоответсвенно конгруэнции 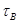 и и 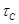 удовлетворяющие определению 2.1. удовлетворяющие определению 2.1.
Определим бинарное отношение 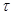 на алгебре на алгебре 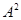 следующим образом: следующим образом:
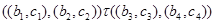
тогда и только тогда, когда
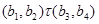
и
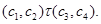
Непосредственной проверкой убеждаемся, что 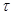 – конгруэнция на алгебре – конгруэнция на алгебре 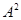 . .
Таким образом осталось показать, что 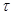 удовлетворяет определению 2.1. удовлетворяет определению 2.1.
Пусть
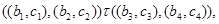
тогда
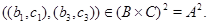
Пусть 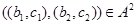 . Это означает, что . Это означает, что 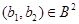 и и 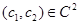 . Но тогда . Но тогда
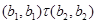
и
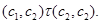
Следовательно,
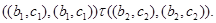
Пусть
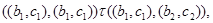
тогда
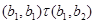
и
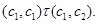
Это означает, что 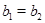 и и 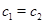 . Таким образом . Таким образом
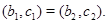
Лемма доказана.
Результаты, полученные в леммах 4.1, 4.2, 4.3 можно теперь сформулировать в виде следующей теоремы.
Теорема
8
Класс всех абелевых алгебр мальцевского многообразия является наследственной формацией.
Пусть 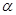 – конгруэнция на алгебре – конгруэнция на алгебре  . . 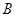 – подалгебра алгебры – подалгебра алгебры  , ,  и и 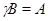 . Тогда введем новое обозначение . Тогда введем новое обозначение
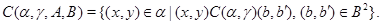
Лемма 4.4.
Пусть определено множество 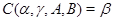 . Тогда . Тогда 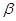 – конгруэнция на – конгруэнция на  , ,
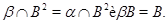
Доказательство:
Так как 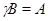 , то для любого элемента , то для любого элемента 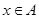 всегда найдется такой элемент всегда найдется такой элемент 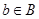 , что , что 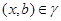 . Следовательно, . Следовательно,
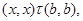
где 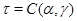 . .
Таким образом 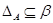 . .
Пусть теперь 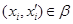 , , 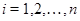 . Тогда . Тогда
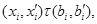
где 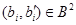 . Следовательно, для любой . Следовательно, для любой 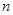 -арной операции -арной операции 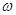 получаем получаем
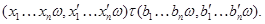
Теперь, поскольку 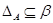 , то по лемме 3.2 , то по лемме 3.2 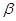 – конгруэнция на – конгруэнция на  . .
Пусть 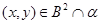 . Тогда, очевидно, . Тогда, очевидно,
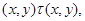
т.е. 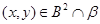 . Так как . Так как
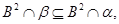
то
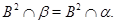
Покажем теперь, что 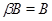 . Допустим противное. Тогда найдется такая пара . Допустим противное. Тогда найдется такая пара 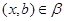 , что , что 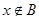 и и 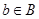 . Из определения . Из определения 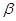 следует, что существует такая пара следует, что существует такая пара 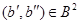 , что , что
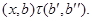
Так как
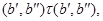
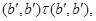
то применяя мальцевский оператор 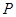 получаем получаем
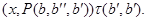
Из леммы 2.2. теперь следует, что 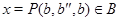 . .
Итак, 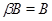 . Лемма доказана. . Лемма доказана.
Подалгебра 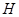 алгебры алгебры  называется нормальной в называется нормальной в  , если , если 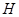 является смежным классом по некоторой конгруэнции алгебры является смежным классом по некоторой конгруэнции алгебры  . .
Лемма 4.5.
Любая подалгебра абелевой алгебры является нормальной.
Доказательство:
Пусть 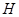 – подалгебра абелевой алгебры – подалгебра абелевой алгебры  . Так как . Так как 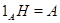 , то по лемме 4.4. на , то по лемме 4.4. на  существует такая конгруэнция существует такая конгруэнция 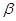 , что , что
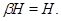
Лемма доказана.
Заключение
Таким образом, в данной работе мы подробно с доказательствами на основании результатов работ [3] и [4] изложили теорию централизаторов конгруэнции универсальных алгебр и рассматрели формационные свойства нильпотентных алгебр работы[2], на основании результатов  3 ввели понятие абелевой алгебры. Используя методы исследования работы [1] доказали следующий основной результат: класс всех универсальных абелевых алгебр из мальцевского многообразия образует наследственную формацию. 3 ввели понятие абелевой алгебры. Используя методы исследования работы [1] доказали следующий основной результат: класс всех универсальных абелевых алгебр из мальцевского многообразия образует наследственную формацию.
Список литературы
Скорняков, Л.А., Элементы общей алгебры. – М.: Наука, 1983. – 272 с.
Шеметков Л.А., Скиба А.Н., Формации алгебраических систем. – М.: Наука, 1989. – 256 с.
Smith J.D. Mal'cev Varieties // Lect. Notes Math. 1976. V.554.
Русаков С.А., Алгебраические 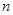 -арные системы. Минск, 1987. – 120 с. -арные системы. Минск, 1987. – 120 с.
Кон П., Универсальная алгебра. М.:Мир, 1968.–351 с.
Ходалевич А.Д., Свойства централизаторов конгруэнции универсальных алгебр // Вопросы алгебры. – 1996.–Вып.10 с. 144–152
Ходалевич А.Д. Формационные свойства нильпотентных алгебр // Вопросы алгебры. – 1992. – Вып.7.–с. 76–85
Ходалевич А.Д. Прикладная алгебра // Лекции по спецкурсу «Универсальные алгебры». Ч1.–Гомель. 2002. – с. 35.
|