Министерство образования и науки РФ
Государственное образовательное учреждение высшего профессионального образования
Вятский государственный гуманитарный университет
Физико-математический факультет
Кафедра высшей математики
Выпускная квалификационная работа
Строение идеалов полукольца натуральных чисел
Выполнила студентка V курса
физико-математического факультета
Вахрушева Ольга Валерьевна
Научный руководитель: д.ф-м.н., профессор кафедры высшей математики Чермных В. В. Рецензент: д.ф-м.н., профессор, заведующий кафедрой высшей математики Вечтомов Е.М.
Киров 2010
Содержание
Введение
Глава 1. Структура идеалов в 
1.1 Базовые понятия и факты
1.2 Описание идеалов в 
Глава 2. Константа Фробениуса
Библиографический список
Приложение 1. Примеры работы программы "FindC" для различных исходных данных
Приложение 2. Описание алгоритма работы программы с помощью блок-схем
Приложение 3. Полный текст программы "FindC"
Введение
Теория полуколец – один из интенсивно развивающихся разделов общей алгебры, являющийся обобщением теории колец. Весомый вклад в ее изучение и развитие внесли Е.М. Вечтомов и В.В. Чермных. Большой интерес для изучения представляет собой полукольцо натуральных чисел с обычными операциями сложения и умножения. Его роль в теории полуколец примерно такая же, как и кольца 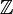 целых чисел в теории колец. Вопросу строения полукольца натуральных чисел посвящена глава в книге В.В. Чермных "Полукольца" [6]. целых чисел в теории колец. Вопросу строения полукольца натуральных чисел посвящена глава в книге В.В. Чермных "Полукольца" [6].
Целью данной квалификационной работы является исследование полукольца натуральных чисел и его строения. Более точно выясняется вопрос, как устроены идеалы этого полукольца, а также осуществляется отыскание либо определение границ расположения константы Фробениуса для некоторых идеалов.
Выпускная квалификационная работа состоит из двух глав. В главе 1 представлены основные определения и теоремы, связанные с полукольцом натуральных чисел, и дано описание его идеалов. Глава 2 посвящена исследованию проблемы нахождения константы Фробениуса.
Глава 1. Структура идеалов в 
1.1 Базовые понятия и факты
Определение 1. Непустое множество S с бинарными операциями "+" и "×" называется полукольцом, если выполняются следующие аксиомы:
1. (S, +) - коммутативная полугруппа с нейтральным элементом 0;
2. (S, ×) - полугруппа с нейтральным элементом 1;
3. умножение дистрибутивно относительно сложения:
a(b + c) = ab + ac, (a + b)c = ac + bc длялюбых a, b, c Î S;
4. 0a = 0 = a0 длялюбого aÎ S.
По этому определению полукольцо отличается от ассоциативного кольца с единицей отсутствием операции вычитания, и именно это вызывает основные трудности при работе с полукольцами.
Несложно показать, что множество натуральных чисел  с обычными операциями сложения и умножения при допущении, что с обычными операциями сложения и умножения при допущении, что 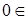  , является полукольцом. , является полукольцом.
Определение 2. Непустое подмножество I полукольца S называется левым идеалом полукольца S, если для любых элементов 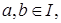 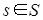 элементы a+b и sa принадлежат I. Симметричным образом определяется правый идеал. Непустое подмножество, являющееся одновременно левым и правым идеалом, называется двусторонним идеалом или просто идеалом полукольца S. элементы a+b и sa принадлежат I. Симметричным образом определяется правый идеал. Непустое подмножество, являющееся одновременно левым и правым идеалом, называется двусторонним идеалом или просто идеалом полукольца S.
В силу коммутативности операции умножения в полукольце  все идеалы являются двусторонними, в дальнейшем будем называть их просто идеалами. все идеалы являются двусторонними, в дальнейшем будем называть их просто идеалами.
Идеал, отличный от полукольца S, называется собственным.
Определение 3. В полукольце S наименьший из всех идеалов, содержащих элемент 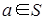 , называется главным идеалом, порожденным элементом a. , называется главным идеалом, порожденным элементом a.
Известно, что кольцо целых чисел 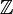 является кольцом главных идеалов. Идеалы в является кольцом главных идеалов. Идеалы в  не обязательно являются главными, но все они конечно порождены. Главные идеалы в не обязательно являются главными, но все они конечно порождены. Главные идеалы в  будем обозначать aN, где a – элемент, порождающий идеал. будем обозначать aN, где a – элемент, порождающий идеал.
Определение 4. Идеал  коммутативного полукольца коммутативного полукольца 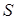 называется конечно порожденным, если найдется конечное множество элементов называется конечно порожденным, если найдется конечное множество элементов 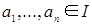 таких, что таких, что
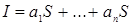
Теорема 1. Произвольный идеал полукольца натуральных чисел конечно порожден.
Доказательство. Пусть  – произвольный идеал из – произвольный идеал из  , , 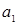 – его наименьший ненулевой элемент. Выберем, если возможно, наименьший элемент из – его наименьший ненулевой элемент. Выберем, если возможно, наименьший элемент из 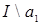 N. В общем случае на очередном шаге будем выбирать наименьший элемент из множества N. В общем случае на очередном шаге будем выбирать наименьший элемент из множества  . Заметим, что выбираемые элементы обязаны быть несравнимыми по модулю . Заметим, что выбираемые элементы обязаны быть несравнимыми по модулю 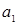 . По этой причине процесс выбора будет конечным, и на некотором шаге получим . По этой причине процесс выбора будет конечным, и на некотором шаге получим
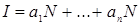
Определение 5. Пусть  – идеал полукольца натуральных чисел. Множество – идеал полукольца натуральных чисел. Множество 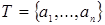 элементов из элементов из  назовем системой образующих идеала, если назовем системой образующих идеала, если 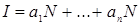 и никакой элемент системы образующих нельзя представить в виде комбинации с неотрицательными коэффициентами остальных элементов системы. и никакой элемент системы образующих нельзя представить в виде комбинации с неотрицательными коэффициентами остальных элементов системы.
Очевидно, что для любого идеала система образующих определяется однозначно. Множество элементов 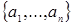 , построенное в доказательстве теоремы 1, является системой образующих. , построенное в доказательстве теоремы 1, является системой образующих.
Если имеется в виду конкретная система образующих идеала, то будем изображать ее в круглых скобках, например: (2,3)={0,2,3,4,…}= \{1}. \{1}.
Аналог теоремы Гильберта о базисе, которая утверждает, что если R – коммутативное кольцо, каждый идеал которого конечно порожден, то любой идеал кольца многочленов над R является конечно порожденным, неверна в классе полуколец, и примером тому служит полукольцо  . Как установлено, идеалы в . Как установлено, идеалы в  конечно порождены. Покажем, что этим свойством не обладает полукольцо конечно порождены. Покажем, что этим свойством не обладает полукольцо  [x]. Пусть I – множество всех многочленов ненулевой степени над [x]. Пусть I – множество всех многочленов ненулевой степени над  . Ясно, что I‒ идеал. Любой из многочленов x, x+1, x+2,…, нельзя нетривиальным образом представить в виде суммы многочленов из I, значит, все эти многочлены необходимо лежат в любой системе образующих идеала I. Таким образом, I не является конечно порожденным, и полукольцевой аналог теоремы Гильберта не верен. . Ясно, что I‒ идеал. Любой из многочленов x, x+1, x+2,…, нельзя нетривиальным образом представить в виде суммы многочленов из I, значит, все эти многочлены необходимо лежат в любой системе образующих идеала I. Таким образом, I не является конечно порожденным, и полукольцевой аналог теоремы Гильберта не верен.
Теорема 2. Пусть 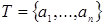 ‒ система образующих идеала ‒ система образующих идеала  полукольца полукольца  . Начиная с некоторого элемента . Начиная с некоторого элемента 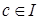 , все элементы идеала образуют арифметическую прогрессию с разностью , все элементы идеала образуют арифметическую прогрессию с разностью 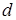 , являющейся наибольшим общим делителем чисел , являющейся наибольшим общим делителем чисел 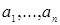 . .
Доказательство. Пусть 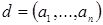 ‒ НОД всех представителей системы образующих идеала ‒ НОД всех представителей системы образующих идеала  . По теореме о линейном представлении НОД . По теореме о линейном представлении НОД 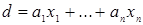 для некоторых целых для некоторых целых 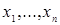 . Положим . Положим 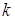 ‒ максимум из абсолютных значений чисел ‒ максимум из абсолютных значений чисел 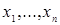 . Тогда элементы . Тогда элементы 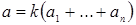 и и 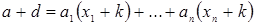 лежат в идеале лежат в идеале  . Очевидно, что . Очевидно, что 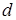 ‒ наименьшее натуральное число, на которое могут отличаться два элемента идеала ‒ наименьшее натуральное число, на которое могут отличаться два элемента идеала  , и , и 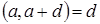 . Обозначим . Обозначим 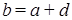 . Пусть . Пусть 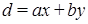 , для некоторых целых , для некоторых целых 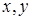 , и одно из них, допустим , и одно из них, допустим 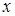 , неположительно. В таком случае рассмотрим число , неположительно. В таком случае рассмотрим число 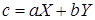 с такими достаточно большими натуральными коэффициентами с такими достаточно большими натуральными коэффициентами 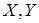 , чтобы для любого целого , чтобы для любого целого 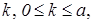 выполнялось выполнялось 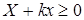 . Тогда для любого такого . Тогда для любого такого 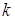 элемент элемент
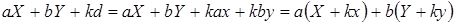
лежит в  . Таким образом, начиная с элемента . Таким образом, начиная с элемента 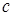 , мы имеем арифметическую прогрессию в точности из , мы имеем арифметическую прогрессию в точности из 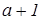 элемента, лежащих в идеале элемента, лежащих в идеале  , причем первый и последний элементы отличаются на , причем первый и последний элементы отличаются на 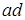 . Прибавляя к каждому из этих элементов, начиная с . Прибавляя к каждому из этих элементов, начиная с 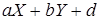 , число , число 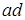 , мы получим следующие , мы получим следующие 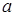 элементов этой же прогрессии. Такую процедуру можно повторять сколь угодно долго, получая элементы прогрессии, очевидно, лежащие в идеале элементов этой же прогрессии. Такую процедуру можно повторять сколь угодно долго, получая элементы прогрессии, очевидно, лежащие в идеале  . Показали, что, по крайней мере, с числа . Показали, что, по крайней мере, с числа 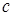 все элементы идеала все элементы идеала  образуют арифметическую прогрессию. образуют арифметическую прогрессию.
Следствие 1. Пусть  ‒ произвольный идеал полукольца ‒ произвольный идеал полукольца  . Существует такое конечное множество . Существует такое конечное множество 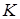 элементов из элементов из  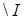 , что , что 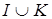 является главным идеалом. является главным идеалом.
Следствие 2. Если система образующих идеала  полукольца полукольца  состоит из взаимно простых в совокупности чисел, то, начиная с некоторого элемента, все последующие натуральные числа будут принадлежать идеалу состоит из взаимно простых в совокупности чисел, то, начиная с некоторого элемента, все последующие натуральные числа будут принадлежать идеалу  . .
Замечание. Пусть 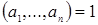 , и , и 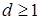 . Между идеалами . Между идеалами  и и 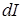 , порожденными системами образующих , порожденными системами образующих 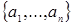 и и 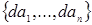 соответственно, существует простая связь, а именно: соответственно, существует простая связь, а именно: 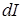 состоит из всех элементов идеала состоит из всех элементов идеала  , умноженных на число , умноженных на число 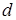 . Тем самым, изучение идеалов полукольца натуральных чисел сводится к идеалам с взаимно простой системой образующих. В дальнейшем будем считать, что образующие . Тем самым, изучение идеалов полукольца натуральных чисел сводится к идеалам с взаимно простой системой образующих. В дальнейшем будем считать, что образующие 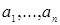 идеала идеала 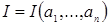 в совокупности взаимно просты и занумерованы в порядке возрастания. в совокупности взаимно просты и занумерованы в порядке возрастания.
Теорема 3. В полукольце  всякая строго возрастающая цепочка идеалов обрывается. всякая строго возрастающая цепочка идеалов обрывается.
Доказательство. Пусть 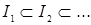 ‒ возрастающая цепочка в ‒ возрастающая цепочка в  . Тогда . Тогда 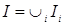 ‒ конечно порожденный идеал с образующими ‒ конечно порожденный идеал с образующими 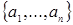 . Каждый . Каждый 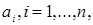 лежит в некоторых идеалах из цепочки, значит, найдется идеал лежит в некоторых идеалах из цепочки, значит, найдется идеал 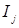 из цепочки, содержащий все элементы из цепочки, содержащий все элементы 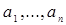 . Получаем . Получаем 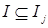 , следовательно, , следовательно, 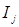 ‒ последний идеал в нашей цепочке. ‒ последний идеал в нашей цепочке.
Из доказанной теоремы делаем вывод о том, что исследуемое полукольцо натуральных чисел является нетеровым.
1.2 Описание идеалов в 
Определение 6. Собственный идеал Pкоммутативного полукольца S называется простым, если 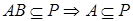 или или 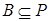 для любых идеалов A и B. для любых идеалов A и B.
Теорема A. Если S – коммутативное полукольцо, то идеал P прост тогда и только тогда, когда 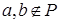 влечет влечет 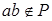 [6]. [6].
Простыми идеалами в  являются, очевидно, нулевой идеал и идеалы p являются, очевидно, нулевой идеал и идеалы p . Идеал, порожденный составным числом, не может быть простым. Более того, если составное число n=ab является элементом системы образующих идеала I, то элементы a,b не лежат в идеале I, и следовательно, I не прост. Таким образом, система образующих простого идеала может состоять только из простых чисел. . Идеал, порожденный составным числом, не может быть простым. Более того, если составное число n=ab является элементом системы образующих идеала I, то элементы a,b не лежат в идеале I, и следовательно, I не прост. Таким образом, система образующих простого идеала может состоять только из простых чисел.
Пусть P – простой идеал в  , не являющийся главным, и , не являющийся главным, и 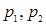 ‒ элементы из его системы образующих. Поскольку ‒ элементы из его системы образующих. Поскольку 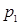 и и 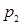 взаимно просты, то по второму следствию теоремы 2 все натуральные числа, начиная с некоторого, лежат в идеале P. Значит, P содержит некоторые степени чисел 2 и 3. В силу простоты идеала P, 2 и 3 будут лежать в P. Идеал, порожденный числами 2 и 3, является единственным простым идеалом, не являющимся главным. взаимно просты, то по второму следствию теоремы 2 все натуральные числа, начиная с некоторого, лежат в идеале P. Значит, P содержит некоторые степени чисел 2 и 3. В силу простоты идеала P, 2 и 3 будут лежать в P. Идеал, порожденный числами 2 и 3, является единственным простым идеалом, не являющимся главным.
Таким образом, простыми идеалами полукольца  являются следующие идеалы, и только они: являются следующие идеалы, и только они:
1. нулевой идеал;
2. главные идеалы, порожденные произвольным простым числом;
3. двухпорожденный идеал (2,3).
Определение 7. Собственный идеал M полукольца S называется максимальным, если 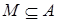 влечет влечет 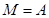 или или 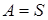 для каждого идеала A в S. для каждого идеала A в S.
Теорема Б. Максимальный идеал коммутативного полукольца прост.[6]
В  нулевой идеал и идеалы, порожденные произвольным простым числом, не являются максимальными, так как включены в идеал (2,3), который не совпадает с ними и с нулевой идеал и идеалы, порожденные произвольным простым числом, не являются максимальными, так как включены в идеал (2,3), который не совпадает с ними и с  . Таким образом, максимальным является двухпорожденный идеал (2,3) – наибольший собственный идеал в . Таким образом, максимальным является двухпорожденный идеал (2,3) – наибольший собственный идеал в  . .
Множество простых идеалов можно упорядочить следующим образом:
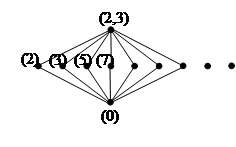
Здесь наибольшим элементом является двухпорожденный идеал (2,3), а наименьшим – нулевой идеал.
Определение 8. Идеал I полукольца S называется полустрогим, если 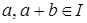 влечет влечет 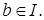
Теорема 6. Полустрогий идеал полукольца  в точности является главным идеалом. в точности является главным идеалом.
Доказательство. Главные идеалы, очевидно, являются полустрогими. Предположим, что в системе образующих полустрогого идеала может быть больше двух образующих. Пусть два элемента m и n – наименьшие в системе образующих идеала, и 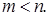 Рассмотрим равенство m+x=n, в нем x очевидно меньше, чем n. Это означает, что x принадлежит идеалу только в том случае, когда элемент x представим в виде x=ms, где Рассмотрим равенство m+x=n, в нем x очевидно меньше, чем n. Это означает, что x принадлежит идеалу только в том случае, когда элемент x представим в виде x=ms, где 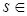  . Тогда n линейно выражается через m, а противоречит тому, что m и n – образующие. . Тогда n линейно выражается через m, а противоречит тому, что m и n – образующие.
Множество полустрогих идеалов можно упорядочить следующим образом:
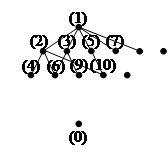
Здесь наибольшим является идеал, порожденный 1, на уровень ниже его находятся идеалы, порожденные простыми числами, еще ниже – порожденные произведением двух простых чисел, дальше трех и так далее.
Определение 9. Идеал I полукольца S называется строгим, если 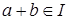 влечет влечет 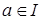 и и 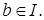
Cтрогий идеал обязательно является полустрогим, а в полукольце  и главным. Идеалы (0) и (1), очевидно, являются строгими. В любых других главных идеалах их образующие можно представить в виде суммы 1 и числа, на 1 меньше образующей, и оба этих слагаемых не будут принадлежать I. Таким образом, строгими идеалами полукольца и главным. Идеалы (0) и (1), очевидно, являются строгими. В любых других главных идеалах их образующие можно представить в виде суммы 1 и числа, на 1 меньше образующей, и оба этих слагаемых не будут принадлежать I. Таким образом, строгими идеалами полукольца  являются только (0) и (1). являются только (0) и (1).
Глава 2. Константа Фробениуса
В теории полугрупп есть понятие константы Фробениуса, им описывается для аддитивной полугруппы, порожденной линейной формой с натуральными коэффициентами, переменные которой независимо принимают целые неотрицательные значения, наибольшее целое число, не являющееся значением указанной формы [4]. Для полукольца  это понятие является неразрывно связанным с элементом это понятие является неразрывно связанным с элементом 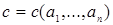 , а именно, они отличаются на 1: константа Фробениуса есть наибольший элемент полукольца, не являющийся элементом идеала, а с – наименьший, начиная с которого все элементы полукольца лежат в идеале. , а именно, они отличаются на 1: константа Фробениуса есть наибольший элемент полукольца, не являющийся элементом идеала, а с – наименьший, начиная с которого все элементы полукольца лежат в идеале.
Лемма 1. Пусть 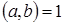 . Тогда для любого натурального . Тогда для любого натурального 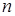 найдутся такие целые найдутся такие целые 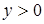 и и 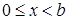 , что , что 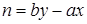 . .
Доказательство. Пусть 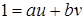 для некоторых целых для некоторых целых 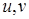 . Тогда . Тогда 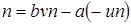 . По теореме о делении с остатком . По теореме о делении с остатком 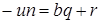 , где , где 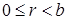 . Отсюда . Отсюда 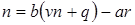 . Взяв . Взяв 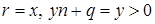 , получаем доказываемое утверждение. , получаем доказываемое утверждение.
Теорема 7. Если 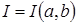 ‒ двухпорожденный идеал и ‒ двухпорожденный идеал и 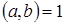 , то , то
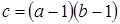
Доказательство. Покажем, что для любого целого 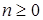 элементы элементы 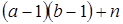 лежат в идеале лежат в идеале  . Действительно, из предыдущей леммы . Действительно, из предыдущей леммы 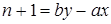 для подходящих для подходящих 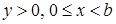 . Тогда . Тогда

Заметим, что 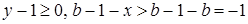 , откуда , откуда 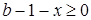 . Таким образом, начиная с . Таким образом, начиная с 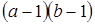 , все числа лежат в идеале , все числа лежат в идеале  . Осталось показать, что . Осталось показать, что 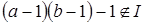 . Предположим, что . Предположим, что 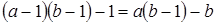 лежит в лежит в  , т.е. , т.е. 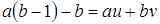 для некоторых для некоторых 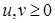 . Очевидно, что мы может выбрать . Очевидно, что мы может выбрать 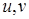 таким образом, чтобы выполнялось таким образом, чтобы выполнялось 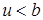 . Тогда . Тогда 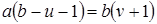 . В силу взаимной простоты образующих получаем . В силу взаимной простоты образующих получаем 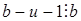 , откуда , откуда 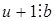 . Это возможно только в том случае, когда . Это возможно только в том случае, когда 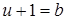 . Но это влечет . Но это влечет 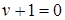 , противоречие. , противоречие.
На XIV Международной олимпиаде по математике, прошедшей в 1984 году, для решения предлагалась задача следующего содержания:
Пусть a,b,c – целые положительные числа, каждые два из которых взаимно просты. Докажите, что наибольшее из целых чисел, которые не представимы в виде xbc+yca+zab (где x,y,z – неотрицательные целые числа), равно 2abc-ab-bc-ca[1].
В незначительной переформулировке эта задача предлагает показать, чему равна константа Фробениуса для идеала, порожденного системой образующих (ab,ac,bc) в полукольце  . .
Удалось найти другое решение этой задачи, а также сделать обобщение.
Теорема 8. Если a, b и с попарно взаимно просты, то
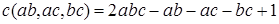 . .
Доказательство. Рассмотрим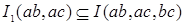 . По теоремам 2 и 5 . По теоремам 2 и 5 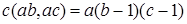 . Значит, начиная с элемента . Значит, начиная с элемента  все элементы вида все элементы вида 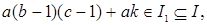 где где 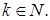 Заметим, что Заметим, что 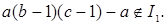 Из условия следует, что Из условия следует, что 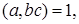 тогда тогда 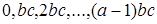 ‒ полная система вычетов по модулю a, обозначим ее (*). ‒ полная система вычетов по модулю a, обозначим ее (*).
Рассмотрим число
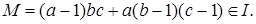
Числа 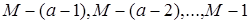 можем получить из системы вычетов (*), прибавляя к ним можем получить из системы вычетов (*), прибавляя к ним 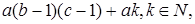 значит, все они лежат в идеале I. Число значит, все они лежат в идеале I. Число 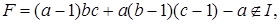 так как так как 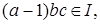 а а 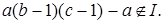 Таким образом, нашли a подряд идущих чисел, принадлежащих идеалу I, и число перед ними, не принадлежащее I. Производя подстановку и преобразовывая выражение Таким образом, нашли a подряд идущих чисел, принадлежащих идеалу I, и число перед ними, не принадлежащее I. Производя подстановку и преобразовывая выражение 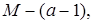 получаем искомый элемент с. получаем искомый элемент с.
Обобщим результат, полученный в теореме 8:
Теорема 9. Пусть 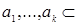  , ,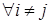 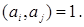 Обозначим Обозначим
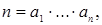 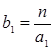 , , 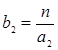 ,…, ,…,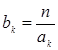
Тогда
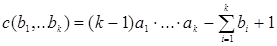 . .
Доказательство. База метода математической индукции для значений k=2,3 доказана в теоремах 7 и 8. Предположив, что выполняется 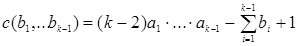 , доказательство проводится аналогично доказательству теоремы 8. , доказательство проводится аналогично доказательству теоремы 8.
Предложение. В 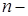 порожденном идеале выполняется порожденном идеале выполняется 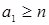 . .
Доказательство. Если 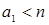 , то найдется, по крайней мере, пара образующих , то найдется, по крайней мере, пара образующих 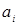 и и 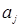 , , 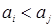 , сравнимых по модулю , сравнимых по модулю 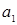 . Тогда . Тогда 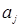 выражается через выражается через 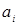 и и 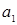 , противоречие. , противоречие.
Крайний случай доказанного выше отношения позволяет найти элемент 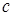 . .
Теорема 10. 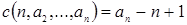 . .
Доказательство. Заметим, что образующие образуют полную систему вычетов по модулю 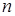 . Рассмотрим еще одну полную систему вычетов по тому же вычету . Рассмотрим еще одну полную систему вычетов по тому же вычету 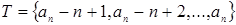 . Для произвольного . Для произвольного 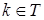 найдется в точности один образующий найдется в точности один образующий 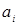 , сравнимый с , сравнимый с 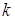 по модулю по модулю 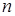 . Тогда . Тогда 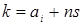 для некоторого для некоторого 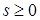 , откуда следует , откуда следует 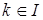 . Получили, что . Получили, что 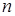 подряд идущих элементов из подряд идущих элементов из 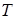 лежат в лежат в  . Поскольку, очевидно, . Поскольку, очевидно,
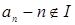 , то , то 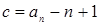
Теорема 11. Если 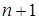 ‒ наименьший образующий ‒ наименьший образующий 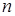 -порожденного идеала -порожденного идеала 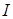 , то , то 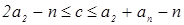 , причем обе оценки точные. , причем обе оценки точные.
Доказательство. Пусть 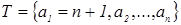 ‒ семейство образующих идеала ‒ семейство образующих идеала 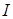 . До полной системы вычетов по модулю . До полной системы вычетов по модулю 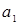 не хватает одного числа. Обозначим через не хватает одного числа. Обозначим через 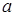 наименьшее число из идеала наименьшее число из идеала 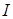 , дополняющее , дополняющее 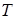 до полной системы. Заметим, что до полной системы. Заметим, что 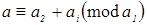 для некоторого для некоторого 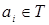 . Отсюда легко получаем, что наименьшее возможное значение, которое может принять . Отсюда легко получаем, что наименьшее возможное значение, которое может принять 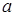 , равно , равно 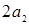 . Число . Число 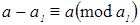 не лежит в идеале не лежит в идеале 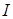 , получаем оценку , получаем оценку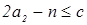 . .
С другой стороны, 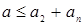 , а в случае равенства числа , а в случае равенства числа 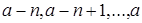 лежат в лежат в 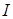 . Действительно, каждое из них сравнимо по модулю . Действительно, каждое из них сравнимо по модулю 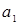 с некоторым образующим и с некоторым образующим и 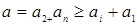 , откуда , откуда 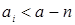 . Это дает оценку . Это дает оценку 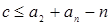 . Не сложно проверить, что точность обеих полученных оценок дают соответственно идеалы . Не сложно проверить, что точность обеих полученных оценок дают соответственно идеалы
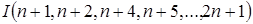
и 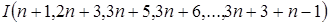 . .
В общем случае проблема нахождения элемента с представляется на данный момент неразрешимой. Однако для дальнейшего ее изучения может быть использована специально разработанная программа "FindC", которая позволяет находить элемент с для введенной системы образующих, причем она может быть не упорядоченной по возрастанию и содержать элементы, линейно выражающиеся через другие.
Действия программы:
1. Сортирует введенные образующие в порядке возрастания (процедура Sort).
2. Проверяет систему на наличие элементов, линейно выражающихся через другие, в случае наличия таковых выводит их и линейную комбинацию (осуществляется с помощью процедуры Lin).
3. Выводит линейно независимую систему образующих, находит их НОД (процедура NOD). Если НОД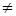 1, то осуществляется деление каждой образующей на НОД, дальнейшая работа происходит с новой системой. 1, то осуществляется деление каждой образующей на НОД, дальнейшая работа происходит с новой системой.
4. Проверяет элементы полукольца  , начиная с 2, на возможность выражения их в виде линейной комбинации системы образующих. При нахождении , начиная с 2, на возможность выражения их в виде линейной комбинации системы образующих. При нахождении 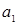 подряд идущих элементов подряд идущих элементов  , принадлежащих идеалу, можно сделать вывод о том, что и последующие элементы также принадлежат идеалу, и программа умножает элемент, на , принадлежащих идеалу, можно сделать вывод о том, что и последующие элементы также принадлежат идеалу, и программа умножает элемент, на 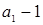 меньше текущего, на НОД, и это произведение будет искомым элементом c. меньше текущего, на НОД, и это произведение будет искомым элементом c.
Библиографический список
1. Абрамов А.М. Квант, №3, 1984. с. 40-41.
2. Атья М., Макдональд И. Введение в коммутативную алгебру [Текст] / М. Атья, И. Макдональд. – М.:Мир,1972.
3. Вечтомов Е.М. Введение в полукольца [Текст] / Е.М. Вечтомов. – Киров: Изд-во ВГПУ, 2000.
4. Коганов Л.М. О функциях Мебиуса и константах Фробениуса полугрупп, порожденных линейными формами специального вида / Межвузовский сборник научных трудов Полугруппы и частичные группоиды, Ленинград, 1987. с. 15-25.
5. Скорняков, Л.А. Элементы теории структур [Текст]/Л.А. Скорняков.– М.: Наука, 1982.
6. Чермных, В.В. Полукольца [Текст]/В.В. Чермных. – Киров: Изд-во ВГПУ, 1997.
Приложение 1.
Примеры работы программы при различных исходных данных.



Приложение 2.
Описание алгоритма работы программы "FindC" с помощью блок-схем.
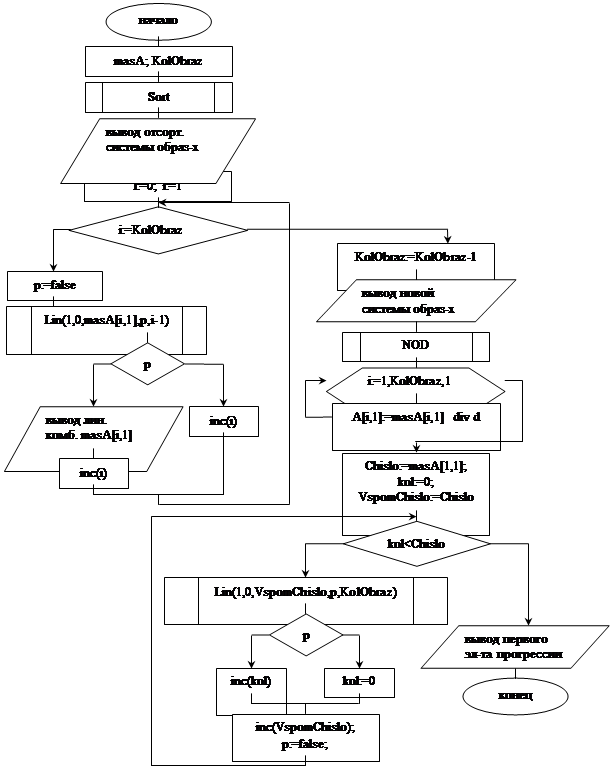
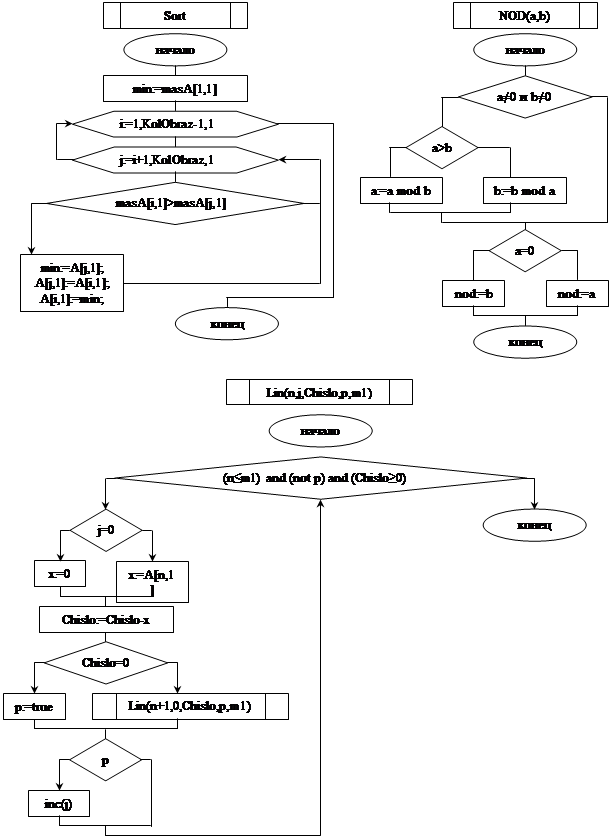
Приложение 3
Полный текст программы "FindC".
unit SearchFirstElementSequence;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls;
type
TForm1 = class(TForm)
Edit: TEdit;
Button1: TButton;
Memo: TListBox;
Button2: TButton;
procedure EditKeyUp(Sender: TObject; var Key: Word; Shift: TShiftState);
procedure Button2Click(Sender: TObject);
procedure Button1Click(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure EditKeyPress(Sender: TObject; var Key: Char);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
masA: variant;
KolObraz: integer;
i, j, l, koef, d, kol, VspomChislo, Chislo: integer;
S: Set of Char = ['0'..'9', ',', #8];
p: boolean;
implementation
{$R *.dfm}
{Сортировка массива}
Procedure SORT;
var min: integer;
begin
min := masA[1,1];;
for i := 1 to KolObraz-1 do
for j := i+1 to KolObraz do
if masA[i,1] > masA[j,1] then begin
min := masA[j,1];
masA[j,1] := masA[i,1];
masA[i,1] := min;
end;
end;
//ищем НОД (алгоритм Евклида)
Function NOD(a,b: integer): integer;
begin
while (a <> 0) and (b <> 0) do
if a > b then a := a mod b
else b := b mod a;
if a = 0 then nod := b
else nod := a;
end;
//проверка на линейность
Procedure Lin (n, j, Chislo: integer; var p: boolean; m1: integer);
var x :integer;
begin
while (n<=m1) and not (p) and (Chislo > 0) do
begin
if j = 0 then x := 0
else x := masA[n,1];
Chislo := Chislo - x;
if Chislo = 0 then p := true
else Lin(n+1, 0, Chislo, p, m1);
if p then masA[n,2] := j;
inc(j);
end;
end;
procedure TForm1.Button1Click(Sender: TObject);
var
list: TStringList;
ss: string;
begin
Memo.Clear;
//разбиениестроки
ss := Edit.Text;
list := TStringList.Create; //создаем список list
//в нем будут хранится коэффициенты, полученные в результате разбиения строки
//с помощью процедуры extractStrings (разделителем будет ',')
extractStrings([','], [], PChar(ss), list);
KolObraz := list.Count; //количество переменных
masA := VarArrayCreate([1,KolObraz,1,2], varInteger); //создание двумерного массива
for i := 1 to KolObraz do
masA[i,1] := StrToInt(list.Strings[i-1]);
list.Free;
SORT;
ss := '';
for i := 1 to KolObraz do ss := ss + ' ' + IntToStr(masA[i,1]);
memo.Items.Add('ИСХОДНАЯ СИСТЕМА ОБРАЗУЮЩИХ В ПОРЯДКЕ ВОЗРАСТАНИЯ:');
memo.Items.Add(ss);
memo.Items.Add('');
memo.Items.Add('ЛИНЕЙНО ЗАВИСИМЫЕ ЭЛЕМЕНТЫ СИСТЕМЫ ОБРАЗУЮЩИХ:');
l := 0; i := 1;
while i <= KolObraz-l do begin
p := false;
Lin(1, 0, masA[i,1], p, i-1);
//если p = true то выводим линейную комбинацию и удаяем этот элемент из массива
ifpthenbegin
//вывод разложения элемента на линейную комбинацию
ss := IntToStr(masA[i,1]) + ' = ';
if i = 2 then ss := ss + IntToStr(masA[i-1,2]) + '*' + IntToStr(masA[i-1,1])
else begin
for j := 1 to i-2 do ss := ss + IntToStr(masA[j,2]) + '*' + IntToStr(masA[j,1]) + ' + ';
ss := ss + IntToStr(masA[i-1,2]) + '*' + IntToStr(masA[i-1,1]);
end;
memo.Items.Add(ss);
//смещаем элементы массива
for j := i to KolObraz-l-1 do begin masA[j,1] := masA[j+1,1]; masA[j,2] := masA[j+1,2]; end;
inc(l);
end
else inc(i);
end;
if l = 0 then memo.Items.Add('нет');
memo.Items.Add('');
KolObraz := KolObraz-l;
memo.Items.Add('ЛИНЕЙНО НЕЗАВИСИМАЯ СИСТЕМА ОБРАЗУЮЩИХ:');
ss := '';
for i := 1 to KolObraz do ss := ss + ' ' + IntToStr(masA[i,1]);
memo.Items.Add(ss);
memo.Items.Add('');
d := NOD(masA[1,1], masA[2,1]);
if KolObraz > 2 then for i := 3 to KolObraz do в := NOD(d, masA[i,1]);
for i := 1 to KolObraz do begin masA[i,1] := masA[i,1] div d; masA[i,2] := 0; end;
Chislo := masA[1,1];
p := false;
kol := 0;
VspomChislo := Chislo;
while kol<Chislo do begin
Lin(1, 0, VspomChislo, p, KolObraz);
if p then inc(kol)
else kol := 0;
inc(VspomChislo);
p := false;
end;
ss := 'ПЕРВЫЙ ЭЛЕМЕНТ В АРИФМЕТИЧЕСКОЙ ПРОГРЕССИИ ' + IntToStr((VspomChislo - kol) * d);
p := false; j := 0;
for i := 1 to KolObraz do masA[i,2] := 0;
Lin(1, j, (VspomChislo - kol) * d, p, KolObraz);
ss := ss + ' = ';
for j := 1 to KolObraz-1 do ss := ss + IntToStr(masA[j,2]) + '*' + IntToStr(masA[j,1]) + ' + ';
ss := ss + IntToStr(masA[KolObraz,2]) + '*' + IntToStr(masA[KolObraz,1]);
ss := ss + ' с разностью ' + IntToStr(d);
memo.Items.Add(ss);
masA := Unassigned;
end;
procedure TForm1.Button2Click(Sender: TObject);
begin
Close;
end;
procedure TForm1.EditKeyPress(Sender: TObject; var Key: Char);
begin
if not (Key in S) then Key := #0
end;
procedure TForm1.EditKeyUp(Sender: TObject; var Key: Word; Shift: TShiftState);
begin
if Edit.Text = '' then Button1.Enabled := false
else Button1.Enabled := true;
end;
procedure TForm1.FormCreate(Sender: TObject);
begin
Button1.Enabled := false;
Memo.Clear;
Edit.Clear;
end;
end.
|