| РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА
ПО ДИСЦИПЛИНЕ
Метрология, стандартизация и технические измерения
Специфика проведения измерений и обработки результатов
Задание 1. Однократное измерение
Условие задания
При однократном измерении физической величины получено показание средства измерения X = 10. Определить, чему равно значение измеряемой величины, если экспериментатор обладает априорной информацией о средстве измерений и условиях выполнения измерений согласно данным таблицы 1.
Экспериментальные данные:
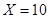
Информация о средстве измерения:
Вид закона распределения нормальный
Значение оценки среднего квадратичного отклонения 
Доверительная вероятность 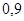
Мультипликативная поправка 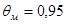
Расчет
Предел, в котором находится значение измеряемой величины без учета поправки определяется как:
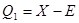 ; ; 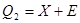 , ,
где Е - доверительный интервал. Значение Е определяется в зависимости от закона распределения вероятности результата измерения. Для нормального закона
 , ,
где t - квантиль распределения для заданной доверительной вероятности. Его выбирают из таблицы интегральной функции нормированного нормального распределения  , при этом следует учитывать, что , при этом следует учитывать, что  . t = 1,64 при P=0,9 . t = 1,64 при P=0,9
 . .
Используя правила округления, получим:
 . .
С учетом поправки значение измеряемой величины определяется как:
 ; ;  . .
Вносим мультипликативную поправку:
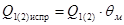 , ,  , , . .
Записываем результат:
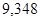 <Q< <Q< ; P=0,9 ; P=0,9
Задание 2. Многократное измерение
Условие задания
При многократном измерении одной и той же физической величины получена серия из 24 результатов измерений 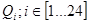 . Эти результаты после внесения поправок представлены в таблице. Определить результат измерения. . Эти результаты после внесения поправок представлены в таблице. Определить результат измерения.
| 
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
| 
|
485
|
484
|
486
|
482
|
483
|
484
|
484
|
481
|
| 
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
| 
|
485
|
485
|
485
|
492
|
484
|
481
|
480
|
481
|
| 
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
24
|
| 
|
484
|
485
|
485
|
484
|
483
|
483
|
485
|
492
|
Для обработки результатов измерений необходимо исключить ошибки. Число измерений лежит в диапазоне 10…15<n<40…50. Поэтому исключение ошибок проводится на основе 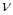 критерия. критерия.
Определяем среднее арифметическое и среднеквадратическое отклонение результатов измерений.
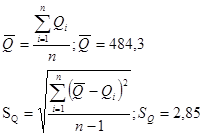
Далее определяем значения 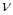 критерия для каждого значения результата измерений критерия для каждого значения результата измерений  по формуле: по формуле:
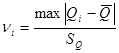
В соответствии с доверительной вероятностью  с учетом с учетом 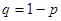 находим из соответствующей таблицы значение находим из соответствующей таблицы значение  , которое зависит от числа измерений , которое зависит от числа измерений 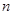 и и  . .
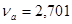
При 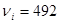 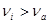 , следовательно значение 492 исключаем как ошибку. , следовательно значение 492 исключаем как ошибку.
Исключение ошибок продолжается до тех пор, пока не будет выполнятся условие 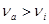 . .
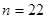
| 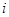
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
| 
|
485
|
484
|
486
|
482
|
483
|
484
|
484
|
481
|
| 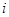
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
| 
|
485
|
485
|
485
|
484
|
481
|
480
|
481
|
484
|
| 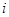
|
17
|
18
|
19
|
20
|
21
|
22
|
|
|
| 
|
485
|
485
|
484
|
483
|
483
|
485
|
|
|
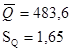
Заново определяем значения 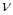 критерия для каждого значения результата измерений критерия для каждого значения результата измерений 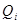 по формуле: по формуле:
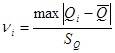
В соответствии с доверительной вероятностью 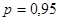 с учетом с учетом 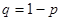 находим из соответствующей таблицы значение находим из соответствующей таблицы значение 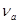 , которое зависит от числа измерений , которое зависит от числа измерений 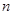 и и 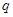 . .
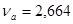
Условие 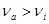 выполняется для всех результатов измерений. выполняется для всех результатов измерений.
Следующим шагом анализа является проверка гипотезы о нормальности распределения оставшихся результатов измерений. Проверка выполняется по составному критерию, так как количество результатов измерений лежит в диапазоне 10…15<n<40…50.
Применяя первый критерий, следует вычислить отношение:
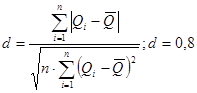
и сравнить с 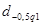 и и 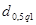 . .
Задаемся рекомендуемой доверительной вероятностью 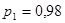 и для уровня значимости и для уровня значимости 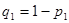 определяем из соответствующей таблицы квантили распределения определяем из соответствующей таблицы квантили распределения 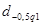 и и 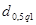 . .
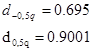
Значение 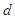 соответствует условию соответствует условию 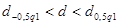 . Первый критерий выполняется. . Первый критерий выполняется.
Применяя второй критерий, задаемся рекомендуемой доверительной вероятностью 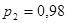 и для уровня значимости и для уровня значимости 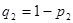 с учетом с учетом 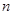 по соответствующим таблицам определяем значения по соответствующим таблицам определяем значения 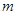 и и  . .
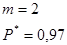
Для  из таблицы для интегральной функции нормированного нормального распределения из таблицы для интегральной функции нормированного нормального распределения  определяем значение определяем значение 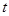 и рассчитываем E: и рассчитываем E:
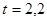  , , 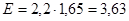
Используя правила округления, получим:
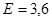
Далее сравниваем значения 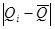 и и 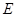 . .
| |
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
| 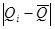
|
1,41
|
0,41
|
2,41
|
1,59
|
1,59
|
0,41
|
0,41
|
1,59
|
| |
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
| 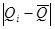
|
1,41
|
1,41
|
1,41
|
0,41
|
2,59
|
3,59
|
2,59
|
0,41
|
| |
17
|
18
|
19
|
20
|
21
|
22
|
|
|
| 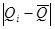
|
1,41
|
1,41
|
0,41
|
0,59
|
0,59
|
1,41
|
|
|
Мы видим, что не более m разностей 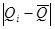 превосходят превосходят 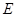 , следовательно второй критерий, а вместе с тем и составной критерий выполняется полностью. Закон распределения можно признать нормальным с вероятностью , следовательно второй критерий, а вместе с тем и составной критерий выполняется полностью. Закон распределения можно признать нормальным с вероятностью 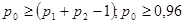 . .
Определяем стандартное отклонение среднего арифметического.
Так как закон распределения нормальный, то стандартное отклонение среднего арифметического определяется следующим образом:
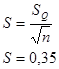
Определяем доверительный интервал
Закон распределения нормальный, следовательно доверительный интервал для заданной доверительной вероятности 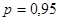 определяется из распределения Стьюдента определяется из распределения Стьюдента 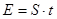 , где , где 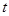 определяется из соответствующей таблицы. определяется из соответствующей таблицы.
  , , 
Используя правила округления, получим:

Результат измерений запишется в виде:

Задание 3. Обработка результатов нескольких серий измерений
Условие задания
При многократных измерениях одной и той же величины получены две серии по 12 (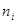 ) результатов измерений в каждой. Эти результаты после внесения поправок представлены в таблице. Вычислить результат многократных измерений. ) результатов измерений в каждой. Эти результаты после внесения поправок представлены в таблице. Вычислить результат многократных измерений.
Серия измерений 1.
| 
|
1
|
2
|
3
|
4
|
5
|
6
|
| 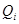
|
485
|
484
|
486
|
482
|
483
|
484
|
| 
|
7
|
8
|
9
|
10
|
11
|
12
|
| 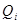
|
484
|
481
|
485
|
485
|
485
|
492
|
Серия измерений 2.
| 
|
1
|
2
|
3
|
4
|
5
|
6
|
| 
|
484
|
481
|
480
|
481
|
484
|
485
|
| 
|
7
|
8
|
9
|
10
|
11
|
12
|
| 
|
485
|
484
|
483
|
483
|
485
|
492
|
Обработка результатов производится для каждой серии отдельно.
Для обработки результатов серий измерений необходимо исключить ошибки. Число измерений лежит в диапазоне 10…15<n<40…50. Поэтому исключение ошибок проводится на основе 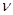 критерия. критерия.
Серия измерений 1.
Определяем среднее арифметическое и среднеквадратическое отклонение результатов серии измерений 1.
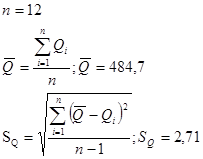
Далее определяем значения 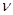 критерия для каждого значения результата серии измерений критерия для каждого значения результата серии измерений 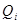 по формуле: по формуле:
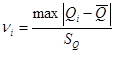
В соответствии с доверительной вероятностью 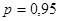 с учетом с учетом 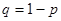 находим из соответствующей таблицы значение находим из соответствующей таблицы значение 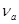 , которое зависит от числа измерений , которое зависит от числа измерений 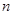 и и 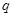 . .
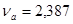
При 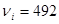 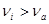 , следовательно, значение 492 исключаем как ошибку. , следовательно, значение 492 исключаем как ошибку.
Исключение ошибок продолжается до тех пор, пока не будет выполнятся условие 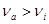 . .
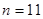
| 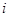
|
1
|
2
|
3
|
4
|
5
|
6
|
| 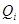
|
485
|
484
|
486
|
482
|
483
|
484
|
| 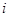
|
7
|
8
|
9
|
10
|
11
|
|
| 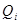
|
484
|
481
|
485
|
485
|
485
|
|
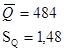
Заново определяем значения 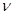 критерия для каждого значения результата серии измерений критерия для каждого значения результата серии измерений 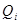 по формуле: по формуле:
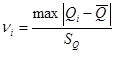
В соответствии с доверительной вероятностью 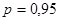 с учетом с учетом 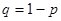 находим из соответствующей таблицы значение находим из соответствующей таблицы значение 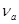 , которое зависит от числа измерений , которое зависит от числа измерений 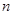 и и 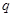 . .
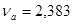
Условие 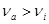 выполняется для всех результатов серии измерений. выполняется для всех результатов серии измерений.
Следующим шагом анализа является проверка гипотезы о нормальности распределения оставшихся результатов серии измерений. Проверка выполняется по составному критерию, так как количество результатов серии измерений лежит в диапазоне 10…15<n<40…50.
Применяя первый критерий, следует вычислить отношение:
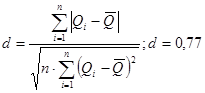
и сравнить с 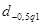 и и 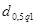 . .
Задаемся рекомендуемой доверительной вероятностью 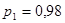 и для уровня значимости и для уровня значимости 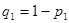 определяем из соответствующей таблицы квантили распределения определяем из соответствующей таблицы квантили распределения 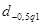 и и 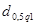 . .
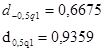
Значение 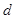 соответствует условию соответствует условию 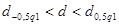 . Первый критерий выполняется. . Первый критерий выполняется.
Применяя второй критерий, задаемся рекомендуемой доверительной вероятностью 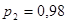 и для уровня значимости и для уровня значимости 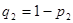 с учетом с учетом 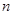 по соответствующим таблицам определяем значения по соответствующим таблицам определяем значения 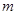 и и 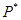 . .
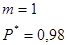
Для 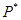 из таблицы для интегральной функции нормированного нормального распределения из таблицы для интегральной функции нормированного нормального распределения 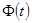 определяем значение определяем значение 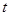 и рассчитываем E: и рассчитываем E:
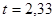 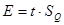 , , 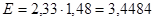 . .
Используя правила округления, получим:
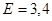
Далее сравниваем значения 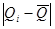 и и 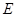 . .
| 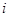
|
1
|
2
|
3
|
4
|
5
|
6
|
| 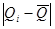
|
1
|
0
|
2
|
2
|
1
|
0
|
| 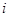
|
7
|
8
|
9
|
10
|
11
|
|
| 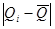
|
0
|
3
|
1
|
1
|
1
|
|
Мы видим, что не более 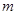 разностей разностей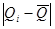 превосходят значение превосходят значение 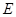 . Следовательно, второй критерий, а вместе с тем и составной критерий выполняются полностью. Закон распределения можно признать нормальным с вероятностью . Следовательно, второй критерий, а вместе с тем и составной критерий выполняются полностью. Закон распределения можно признать нормальным с вероятностью
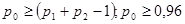 . .
Серия измерений 2.
Определяем среднее арифметическое и среднеквадратическое отклонение результатов серии измерений 2.
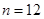
| 
|
1
|
2
|
3
|
4
|
5
|
6
|
| 
|
484
|
481
|
480
|
481
|
484
|
485
|
| 
|
7
|
8
|
9
|
10
|
11
|
12
|
| 
|
485
|
484
|
483
|
483
|
485
|
492
|
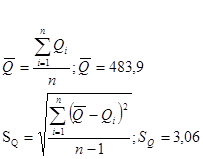
Далее определяем значения 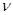 критерия для каждого значения результата серии измерений критерия для каждого значения результата серии измерений 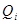 по формуле: по формуле:
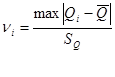
В соответствии с доверительной вероятностью 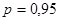 с учетом с учетом 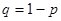 находим из соответствующей таблицы значение находим из соответствующей таблицы значение 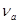 , которое зависит от числа измерений , которое зависит от числа измерений 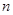 и и 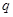 . .
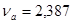
При 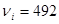 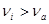 , следовательно значение 492 исключаем как ошибку. , следовательно значение 492 исключаем как ошибку.
Исключение ошибок продолжается до тех пор, когда не будет выполнятся условие 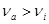 . .
| 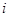
|
1
|
2
|
3
|
4
|
5
|
6
|
| 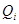
|
484
|
481
|
480
|
481
|
484
|
485
|
| 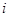
|
7
|
8
|
9
|
10
|
11
|
|
| 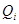
|
485
|
484
|
483
|
483
|
485
|
|
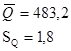
Заново определяем значения 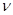 критерия для каждого значения результата серии измерений критерия для каждого значения результата серии измерений 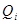 по формуле: по формуле:
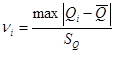
В соответствии с доверительной вероятностью 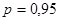 с учетом с учетом 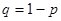 находим из соответствующей таблицы значение находим из соответствующей таблицы значение 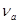 , которое зависит от числа измерений , которое зависит от числа измерений 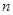 и и 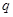 . .
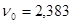
Условие 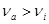 выполняется для всех результатов серии измерений. выполняется для всех результатов серии измерений.
Следующим шагом анализа является проверка гипотезы о нормальности распределения оставшихся результатов серии измерений. Проверка выполняется по составному критерию, так как количество результатов серии измерений лежит в диапазоне 10…15<n<40…50.
Применяя первый критерий, следует вычислить отношение:
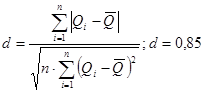
и сравнить с 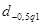 и и 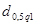 . .
Задаемся рекомендуемой доверительной вероятностью 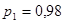 и для уровня значимости и для уровня значимости 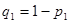 определяем из соответствующей таблицы квантили распределения определяем из соответствующей таблицы квантили распределения 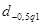 и и 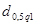 . .
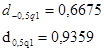
Значение 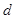 соответствует условию соответствует условию 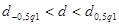 . Первый критерий выполняется. . Первый критерий выполняется.
Применяя второй критерий, задаемся рекомендуемой доверительной вероятностью 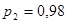 и для уровня значимости и для уровня значимости 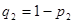 с учетом с учетом 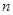 по соответствующим таблицам определяем значения по соответствующим таблицам определяем значения 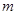 и и 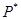 . .
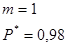
Для 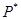 из таблицы для интегральной функции нормированного нормального распределения из таблицы для интегральной функции нормированного нормального распределения 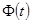 определяем значение определяем значение 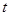 и рассчитываем E: и рассчитываем E:
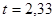 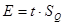 , , 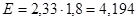 . .
Используя правила округления, получим:
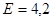
Далее сравниваем значения 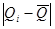 и и 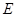 . .
| 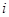
|
1
|
2
|
3
|
4
|
5
|
6
|
| 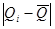
|
0,82
|
2,18
|
3,18
|
2,18
|
0,82
|
1,82
|
| 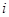
|
7
|
8
|
9
|
10
|
11
|
|
| 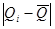
|
1,82
|
0,82
|
0,18
|
0,18
|
1,82
|
|
Мы видим, что не более 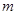 разностей разностей 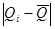 превосходят значение превосходят значение 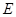 . Следовательно второй критерий, а вместе с тем и составной критерий выполняется полностью. Закон распределения можно признать нормальным с вероятностью . Следовательно второй критерий, а вместе с тем и составной критерий выполняется полностью. Закон распределения можно признать нормальным с вероятностью 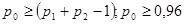 . .
Далее необходимо проверить значимость различия средних арифметических серий.
Для этого необходимо вычислить моменты закона распределения разности:
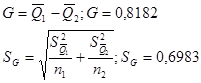
Задавшись доверительной вероятностью 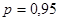 , определяем из соответствующих таблиц интегральной функции нормированного нормального распределения , определяем из соответствующих таблиц интегральной функции нормированного нормального распределения 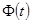 значение значение 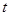 и сравниваем и сравниваем  с с 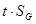 . .
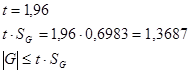
Условие 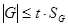 выполняется. Различие между средними арифметическими в сериях с доверительной вероятностью выполняется. Различие между средними арифметическими в сериях с доверительной вероятностью 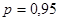 можно признать незначимым. можно признать незначимым.
Далее необходимо проверить равнорассеянность результатов измерений в сериях.
Для этого определяем значение:
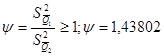
И, задавшись доверительной вероятностью 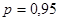 , определяем из соответствующих таблиц значение аргумента интегральной функции распределения вероятности Фишера , определяем из соответствующих таблиц значение аргумента интегральной функции распределения вероятности Фишера 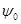 . .
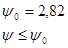
Условие 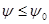 выполняется. Серии с доверительной вероятностью выполняется. Серии с доверительной вероятностью 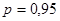 считаем рассеянными. считаем рассеянными.
Выше было показано, что серии равнорассеяны и с незначимым различием средних арифметических. Исходя из этого все результаты измерений объединяются в единый массив и затем для него выполняется обработка по алгоритму, согласно которому необходимо определить оценку результата измерения  и среднеквадратического отклонения и среднеквадратического отклонения 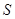 . .
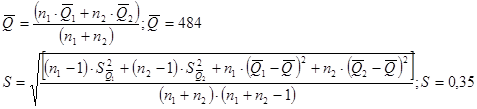
Задавшись доверительной вероятностью 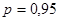 , определяем из таблиц распределения Стьюдента значение , определяем из таблиц распределения Стьюдента значение 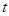 для числа степеней свободы для числа степеней свободы
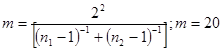
Затем определяем доверительный интервал 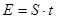 : :
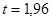
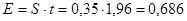
Используя правила округления, получим:
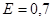
Результат измерений запишется в виде:
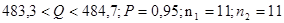 . .
Задание 4. Функциональные преобразования результатов измерений (косвенные измерения)
Условие задания
При многократных измерениях независимых величин 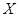 и и 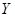 получено по 12 (n) результатов измерений. Эти результаты после внесения поправок представлены в таблице 2. Определить результат вычисления получено по 12 (n) результатов измерений. Эти результаты после внесения поправок представлены в таблице 2. Определить результат вычисления 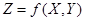 , (вид функции , (вид функции 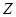 и характер величин и характер величин 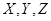 представлены в таблице 3). представлены в таблице 3).
Вид функциональной зависимости 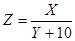 . .
Характер и единицы величин:
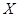 - ЭДС, мВ; - ЭДС, мВ;
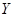 - сопротивление, Ом; - сопротивление, Ом;
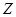 - сила тока, А. - сила тока, А.
Обработка результатов измерений величин 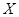 и и 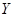 проведена в задании 3 первой расчетно-графической работы. проведена в задании 3 первой расчетно-графической работы.
Средние значения и среднеквадратические отклонения для величин 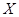 и и 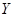 имеют вид имеют вид
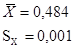
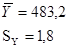
Гипотеза о нормальности распределения величин 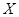 и и 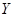 подтверждается. подтверждается.
Определим оценку среднего значения функции:
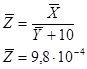
Определим поправку
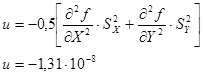
Определим оценку стандартного отклонения функции
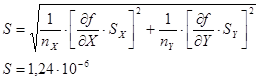
Определяем доверительный интервал для функции
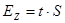
Законы распределения вероятности результатов измерения 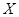 и и 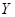 признаны нормальными, признаны нормальными, 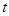 можно определить для принятой доверительной вероятности можно определить для принятой доверительной вероятности 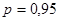 из таблиц для распределения Стьюдента. При этом число степеней свободы из таблиц для распределения Стьюдента. При этом число степеней свободы 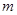 определяется из выражения определяется из выражения
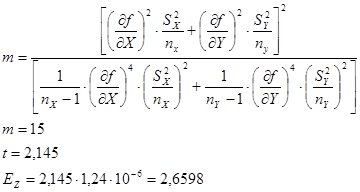
Используя правила округления, получим:
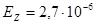
Результат запишется в виде:
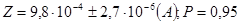
Задание 5. Обработка экспериментальных данных при изучении зависимостей
Условие задания
При многократных совместных измерениях величин 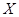 и и 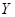 получено по 20 (n) пар результатов измерений. Эти результаты после внесения поправок представлены в таблице 4. Определить уравнение регрессии получено по 20 (n) пар результатов измерений. Эти результаты после внесения поправок представлены в таблице 4. Определить уравнение регрессии 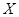 по по 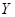 : : 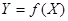 . .
| 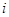
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
| 
|
61;602
|
62;613
|
63;620
|
64;631
|
65;639
|
66;648
|
67;656
|
| 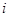
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
| 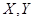
|
68;662
|
69;667
|
70;682
|
9;87
|
19;188
|
29;286
|
39;386
|
| 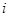
|
15
|
16
|
17
|
18
|
19
|
20
|
|
| 
|
49;485
|
59;575
|
69;667
|
79;770
|
89;868
|
99;966
|
|
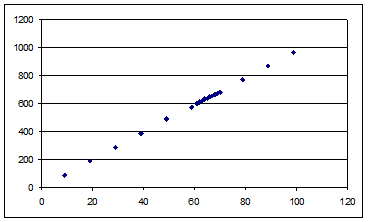
В качестве прямой регрессии будем использовать прямую вида
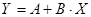 . .
Параметры прямой определим по методу наименьших квадратов.
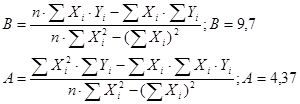
Далее проверяем правильность выбора вида уравнения регрессии. Для этого следует применить критерии серий и инверсий.
Рассчитываем отклонения экспериментальных значений от соответствующих расчетных значений, рассчитанных для того же аргумента:
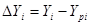
| 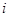
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
| 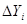
|
-4,67
|
-0,67
|
0,33
|
3,33
|
5,33
|
-1,67
|
5,93
|
| 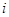
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
| 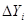
|
7,23
|
4,53
|
5,83
|
4,13
|
3,43
|
1,73
|
-1,97
|
| 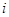
|
15
|
16
|
17
|
18
|
19
|
20
|
|
| 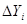
|
-6,67
|
-6,67
|
-1,37
|
-0,67
|
0,33
|
1,33
|
|
последовательность ∆Yi записана по мере возрастания Х
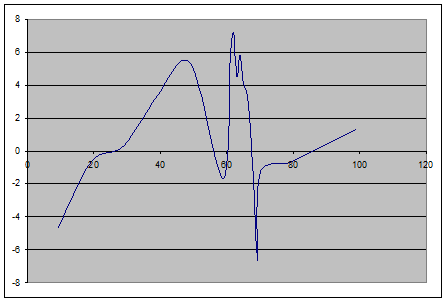
Критерий серий:
Рассчитываем число серий в полученной последовательности: N=6
Задавшись доверительной вероятностью 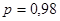  , для n=20 определяем по таблице допустимые границы , для n=20 определяем по таблице допустимые границы 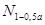 и и 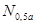 : :
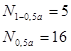
Критерий инверсий:
Рассчитываем число инверсий А в полученной последовательности 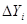 : А=106. : А=106.
Задавшись доверительной вероятностью 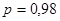 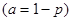 для n=20 определяем по таблице допустимые границы для n=20 определяем по таблице допустимые границы 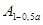 и и  : :
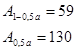
Оба неравенства выполняются 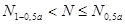 и и 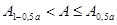 . Поэтому можно считать, что рассчитанное уравнение регрессии достоверно описывает экспериментально исследуемую зависимость. . Поэтому можно считать, что рассчитанное уравнение регрессии достоверно описывает экспериментально исследуемую зависимость.
|