| Дипломная работа
на тему
Система распознавания объектов в миллиметровом диапазоне радиоволн
Введение
Актуальность работы.
Определённые достижения в области распознавания классов автомобильной и гусеничной техники были получены в ряде НИИ бывшего СССР при разработке образцов станций разведки наземных движущихся целей. Однако, некоторые проблемы в области создания банка данных о признаках распознавания реальных целей, а также существенные ограничения на возможности реализации программного и алгоритмического обеспечения не позволили в 80-90-х годах решить эту задачу. Указанное приводит к необходимости продолжения исследований по синтезу и анализу алгоритмов обнаружения и предварительной классификации неподвижных целей (объекты искусственного или естественного происхождения, объекты автобронетанковой техники среди искусственных сооружений) и распознавания движущихся малоразмерных наземных целей (МНЦ).
Анализ исследований, проводящихся в настоящий момент в странах с развитой экономикой, что проблема распознавания движущихся и обнаружения неподвижных целей по–прежнему актуальна и далека от своего завершения.
В отдельных работах отмечено, что перспективным направлением при решении проблемы селекции неподвижных целей является применение методов поляризационной селекции. Использование поляризационной обработки обеспечивает ряд преимуществ по сравнению с традиционными методами обработки сигналов, таких как:
– возможность использования полной эффективной площади рассеяния (ЭПР) объекта, что особенно важно при селекции малоконтрастных целей;
– применение тонкой поляризационной структуры отраженного сигнала при решении задач обнаружения МНЦ, укрытых растительностью;
– возможность использования видов поляризации, отличных от линейной, для повышения РЛ контраста.
Уместно отметить, что применение процедур классификации МНЦ поляриметрическими РЛС к настоящему времени практически не рассмотрены вследствие отсутствия возможности сравнительной оценки признаков распознавания для реальных целей.
Широкий круг исследований, посвященных решению задачи распознавания классов целей по спектральным отличиям отражённых от них сигналов, не привёл к появлению алгоритмов, устойчивых к изменению условий РЛ наблюдения: ракурса, скорости, вида трассы.
Таким образом, проведенные к настоящему моменту исследования эффективности использования поляризационных и спектральных характеристик для решения задач распознавания движущихся и селекции неподвижных МНЦ обладают рядом существенных недостатков:
1. Систематизированные сведения об отражающих свойствах и поляризационных и спектральных характеристиках широкого круга образцов военной техники и местных предметов к настоящему моменту отсутствуют.
2. Отсутствуют эффективные алгоритмы повышения радиолокационного контраста МНЦ на фоне подстилающей поверхности.
3. Не разработаны достаточно эффективные и реализуемые на практике алгоритмы селекции неподвижных МНЦ на фоне мешающих отражений.
4. Отсутствуют реализуемые на практике алгоритмы классификации движущихся МНЦ по совокупности поляризационных и спектральных признаков.
В связи с этим актуальной научно–технической задачей
является разработка системы интелектуального распознавания классов движущихся и селекции неподвижных МНЦ на фоне подстилающей поверхности в интересах построения РЛС разведки и целеуказания повышенной информативности.
Актуальность задачи обусловлена:
необходимостью повышения информативности радиолокационных средств разведки и целеуказания; неизученностью отражающих свойств реальных объектов военной техники и подстилающей поверхности; целесообразностью разработки алгоритмов распознавания движущихся и селекции неподвижных целей на фоне помеховых отражений от подстилающей поверхности.
Объект исследования
представляет собой РЛС разведки и целеуказания повышенной информативности, позволяющую решить задачи селекции неподвижных и классификации движущихся МНЦ.
Предметом исследования
являются алгоритмы и устройства для селекции неподвижных и распознавания движущихся МНЦ на основе спектральных и поляризационных параметров отражённого от них сигнала.
Целью работы
является повышение эффективности распознавания движущихся и поляризационной селекции неподвижных малоразмерных наземных целей в интересах радиолокационных станций разведки и целеуказания.
Поставленная цель достигается решением следующих задач,
составляющих основные этапы исследования:
1. Анализ физических предпосылок селекции движущихся МНЦ по спектральным параметрам. Разработка алгоритмов и устройств обнаружения МНЦ и оценка их эффективности.
2. Разработка алгоритмов обнаружения МНЦ и оценка их эффективности.
3. Синтез алгоритмов классификации движущихся МНЦ и оценка их эффективности.
4. Разработка системы интеллектуального распознавания классов движущихся и селекции неподвижных МНЦ на фоне подстилающей поверхности в интересах построения РЛС разведки и целеуказания повышенной информативности.
Методы исследований.
Методологической основой развиваемых методов, алгоритмов и разрабатываемых устройств служат:
–
элементы теории вероятностей, математической статистики и случайных процессов;
–
методы статистической теории обнаружения и классификации случайных сигналов;
–
методы статистической теории радиолокации;
–
методы радиофизики, электродинамики и теории распространения радиоволн.
В рамках научно–технической задачи, решаемой в работе, должны быть получены следующие результаты:
1. Разработана математическая модель.
2. Разработано информационное обеспечение.
3. Оценена эффективность полученных алгоритмов.
4. Разработано программное обеспечение.
На защиту выносятся следующие вопросы,
соответствующие основе рассматриваемой задачи.
1. Совокупность аналитических соотношений для вероятностных характеристик поляризационных параметров сигналов, отраженных от МНЦ, наблюдаемых на фоне мешающих отражений.
2. Алгоритмы обнаружения сигналов, отраженных от неподвижных МНЦ, по поляризационным и корреляционным свойствам.
3. Алгоритмы распознавания классов движущихся МНЦ, методика оценки их эффективности.
Практическая значимость работы
состоит в следующем:
1. В разработке программного комплекса для определения спектральных и поляризационных характеристик реальных целей.
2. В получении данных о спектральных свойствах и ПХ МНЦ, позволяющих осуществлять анализ эффективности радиолокационных систем разведки и целеуказания.
3. В разработке методов поляризационной селекции неподвижных МНЦ, наблюдаемых на фоне подстилающей поверхности и местных предметов.
Достоверность результатов диссертационной работы
определяется следующими факторами:
В основе исследований, проведенных в работе, лежат хорошо апробированные ранее положения статистической теории радиолокации. Обработка данных и сопоставление их с теоретическими базируется на методах математической статистики.
1. АНАЛИЗ МЕТОДОВ И ПАРАМЕТРОВ ВОЗМОЖНЫХ ПРИЗНАКОВ КЛАССИФИКАЦИИ И ОБНАРУЖЕНИЯ НАЗЕМНЫХ ОБЪЕКТОВ
1.1 Формирование алфавитов классов (типов) целей для системы распознавания объектов
Различаемые классы (типы) целей составляют определенный алфавит, подобный алфавиту букв русского (английского и т.п.) языка. Выбор алфавита классов предопределяет как эффективность использования систем селекции–распознавания, так и трудности, возникающие при их реализации, а значит и стоимость их преодоления.
Информация, используемая для селекции–распознавания, содержится в совокупности принимаемых радиолокационных сигналов. Однако чаще всего, чтобы селектировать–распознать цель, используют определенные измеренные признаки цели, которые сопоставляют в соответствии с алгоритмами распознавания с известными (эталонными) признаками.
Совокупности признаков, необходимые для распознавания в тех или иных алфавитах классов, образуют признаковые пространства или, иначе, рабочие словари [16,17] признаков. Целесообразность совокупного выбора алфавитов классов, признаковых пространств и алгоритмов распознавания оценивают на основе известного системотехнического критерия «эффективность-стоимость». Эффективность распознавания характеризуют его влиянием на показатели качества потребителей информации распознавания или непосредственно показателями качества распознавания.
В общем случае формирование алфавитов классов (кластеров) характерно не только для задач радиолокационного распознавания, но и для других кибернетических задач теории и техники распознавания образов [14]. Эти задачи выделяют иногда как задачи кластерного анализа [16]. В качестве кластеров могут выступать не только классы, но и их подклассы. Состав алфавита определяется задачами потребителей локационной информации, с одной стороны, и возможностями средств локации при тех или иных признаковых пространствах – с другой.
Применительно к РЛС, учитывая возможности реализации методов селекции в спектральной области и поляриметрической обработки, существенно различать движущиеся цели (класс ω1
) и неподвижные (класс ω2
).
Также важна зачастую дополнительная выходная информация относительно класса движущихся целей ω1
: гусеничная это техника (подкласс ω11
) или колесная (подкласс ω12
).
В свою очередь, класс неподвижных объектов ω2
включает подкласс местных предметов (подкласс ω21
) и подкласс техники (подкласс ω22
), который, собственно, и включает объекты разведки РЛС разведки и целеуказания.
Для подкласса местных предметов можно продолжить дальнейшую градацию – на субклассы предметов антропогенного характера (ω211
) и естественного (ω212
) характера.
Графически предложенная схема классификации объектов может быть представлена рис.1.1.
Чем шире и достовернее информация селекции–распознавания, тем эффективнее, в принципе, она может быть использована. Однако чрезмерное расширение алфавита классов снижает достоверность информации (особенно при не очень высоких отношениях сигнал–шум), требует привлечения новых признаков.
В общем случае оптимизация алфавита классов представляет собой непростую комплексную (локационную, тактическую и экономическую) задачу, решаемую путем сравнения вариантов с использованием методов физико–математического моделирования после определения окончательного технического облика проектируемой РЛС.

Рис. 1.1. Схема классификации объектов
Таким образом, была предложена схема классификации классов объектов, объединяющая задачи селекции-распознавания МНЦ и местных предметов.
Предварительный анализ путей внедрения в РЛС разведки и целеуказания режима обнаружения и распознавания малоподвижных и неподвижных объектов, предложений по их технической реализации и экспериментальных данных позволил сформулировать следующий алгоритм обнаружения и распознавания неподвижных целей, приведенный на рис.1.2.
Поясним отдельные этапы этого алгоритма.
1. Ввод значений вектора входного сигнала X,
который может быть представлен в форме
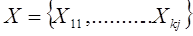 , ,
где 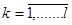 , l – размер выборки от k–го элемента разрешения; , l – размер выборки от k–го элемента разрешения;
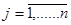 , j – количество элементов разрешения по дальности. , j – количество элементов разрешения по дальности.
2. Предварительное обнаружение по энергетическому параметру 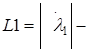 мере заметности цели ((L1)2
– максимум ЭПР цели для оптимальной поляризации) или комплексному параметру. Ранее в [26] были показана возможность и синтезирован алгоритм обнаружения по перспективным параметрам. мере заметности цели ((L1)2
– максимум ЭПР цели для оптимальной поляризации) или комплексному параметру. Ранее в [26] были показана возможность и синтезирован алгоритм обнаружения по перспективным параметрам.
3. Селекция по протяженности цели. При разработке этого подалгоритма необходимо учесть следующие предпосылки:
а) предполагаемая величина элемента разрешения узкополосных РЛС по дальности 10 – 15 м;
б) цели являются пространственно–сосредоточенными, т.е. занимают одну ячейку разрешения по дальности, а мешающие отражения – пространственно-распределенными, т.е. занимают более одной ячейки разрешения по дальности;
в) наибольшая радиальная протяженность лоцируемого наземного объекта разведки РЛС порядка 7–8 м. Следовательно, если по результатам предварительного обнаружения по энергетическому параметру цель занимает несколько смежных элементов разрешения по дальности, то принимается решение, что зондируемый объект относится к подклассу местных предметов (подкласс ω21
).
Если же зондируемый объект располагается в одном элементе разрешения, то принимается решение, что зондируемый объект относится к подклассу техники (подкласс ω22
).
4. Адаптивная фильтрация сигнала на фоне мешающих отражений. Основная задача этого этапа – повышение соотношения сигнал/шум на основе алгоритмов поляризационно–временной селекции, результаты синтеза которых будут приведены далее.


Рисунок 1.2. Алгоритм обнаружения и распознавания неподвижных целей
5. Расчет поляризационных и временных параметров. На этом этапе осуществляется расчет поляризационных и временных параметров в соответствии с соотношениями, рассмотренными в [28–31].
6. Процедуры распознавания (обнаружения) целей по вектору признаков. На основании вычисленных на этапе 5 поляризационных и временных параметров, составляющих вектор признаков, осуществляется распознавание (обнаружение) целей. Алгоритмы распознавания (обнаружения) целей по вектору признаков будут рассмотрены в дальнейшем.
1.2 Характеристики сигналов, отражённых от движущихся объектов
1.2.1 Анализ физических факторов, определяющих спектр сигнала от движущейся цели
Физическими предпосылками для решения задачи распознавания классов движущихся наземных целей являются как различия в частоте колебаний подрессоренной массы цели при ее движении по трассе, так и особенности вибрации ее конструктивных элементов [21, 12]. Механизмами возникновения спектральных отличий для классов колесной и гусеничной техники являются:
1. Вибрации объекта, обусловленные работой двигателя
, которые являются следствием как вращения неуравновешенных частей механизмов двигателя, так и процессов ударного сгорания топливной смеси в цилиндрах. Для дизельных и карбюраторных двигателей спектр отраженного сигнала содержит гармоники основной частоты коленчатого вала, значение которой лежит в диапазоне частот 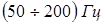 . Положение спектральных линий меняется в зависимости от числа оборотов двигателя, а следовательно и от скорости движения объекта. . Положение спектральных линий меняется в зависимости от числа оборотов двигателя, а следовательно и от скорости движения объекта.
2. Вибрации объекта при движении по неровностям трассы без отрыва от ее поверхности.
Такие вибрации зависят от формы пространственного спектра неровностей дороги, собственных колебательных характеристик объекта как механической системы, скорости движения и типа грунта. Составляющая спектра, связанная с этими вибрациями, имеет сплошной вид с максимумами, обусловленными АЧХ подвески ходовой части и характеристиками грунта. Резонансные частоты подвески у тяжелых и легких гусеничных объектов составляют соответственно 1,1 и 1,4 Гц. Для гусеничной техники характерны также колебания, возбуждаемые при движении катков по неровностям трассы, сосредоточенные в диапазоне частот 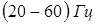 . При движении колесной техники по неровностям дороги колебания возбуждаются: за счет колебания кузова в диапазоне частот . При движении колесной техники по неровностям дороги колебания возбуждаются: за счет колебания кузова в диапазоне частот 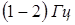 ; за счет колебания мостов в диапазоне частот ; за счет колебания мостов в диапазоне частот 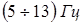 ; за счет колебания двигателя на подвеске в диапазоне частот ; за счет колебания двигателя на подвеске в диапазоне частот 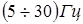 . Основная энергия сигнала при движении колесной техники по неровностям дороги приходится на диапазон частот . Основная энергия сигнала при движении колесной техники по неровностям дороги приходится на диапазон частот 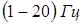 , а максимум спектральной плотности – на диапазон , а максимум спектральной плотности – на диапазон 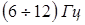 . .
3. вибрации, связанные с наличием гусеничного движителя
возникают из–за движения опорных катков по профилированной гусенице и возбуждают колебания на «траковой» частоте и ее гармониках. Спектр этого колебания зависит от скорости движения объекта, а значение «траковой» частоты можно определить из соотношения
F
=
V
/
L
(1.1)
где L – длина гусеницы, м; V – скорость объекта, м/с.
При скоростях движения 3–15 м/с значение частоты «траковой» составляющей в спектре находится в диапазоне 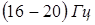 за счет многополярности подвески гусениц. Значение частот колебаний, возбуждаемых вследствие нецентрированности колес и катков, можно определить из соотношения за счет многополярности подвески гусениц. Значение частот колебаний, возбуждаемых вследствие нецентрированности колес и катков, можно определить из соотношения
F
=
V
/
d
(1.2)
где V – скорость движения, м/с; в – диметр катка, м.
Как видно из (1.2), спектр колебаний зависит от скорости движения. При движении со скоростями 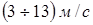 он сосредоточен в диапазоне частот от 0,5 до единиц герц. Удары траков гусениц о дорогу с твердым покрытием приводят к возбуждению колебаний, значение частоты которых зависит от скорости движения и лежит в диапазоне от 10 до 60 Гц. он сосредоточен в диапазоне частот от 0,5 до единиц герц. Удары траков гусениц о дорогу с твердым покрытием приводят к возбуждению колебаний, значение частоты которых зависит от скорости движения и лежит в диапазоне от 10 до 60 Гц.
Физическими предпосылками для решения задачи распознавания классов наземных целей являются как различия в частоте колебаний подрессоренной массы цели при ее движении по трассе, так и особенности вибраций ее конструктивных элементов. Так, например, амплитуда колебаний конструктивных элементов для танка составляет (0,01…0,25) мм, а для автомобиля (0,01…3) мм. Частота вибраций соответственно лежит в пределах (200…2000) …..Гц и (0,5…30) Гц. Представив модель цели в виде совокупности блестящих точек (БТ), результирующий сигнал на входе антенны РЛС можно записать в виде:
 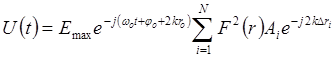 (1.3) (1.3)
где 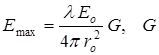 – коэффициент усиления антенны, – коэффициент усиления антенны, 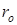 – расстояние до центра масс (ЦМ) цели, – расстояние до центра масс (ЦМ) цели, 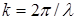 – волновое число, – волновое число, 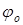 – начальная фаза, – начальная фаза, 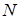 – количество БТ цели, – количество БТ цели, 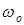 – несущая частота, – несущая частота, 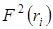 – диаграмма обратного рассеяния по мощности – диаграмма обратного рассеяния по мощности 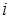 –ой БТ, –ой БТ, 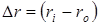 – разность хода волн от ЦМ до – разность хода волн от ЦМ до 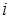 –й БТ. –й БТ.
Величина 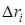 определяет изменение фазы определяет изменение фазы 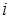 –й БТ –й БТ 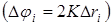 . Можно показать, что разность хода волн . Можно показать, что разность хода волн 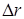 равна равна
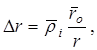 (1.4) (1.4)
где 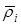 – математическое ожидание расстояния от центра масс до – математическое ожидание расстояния от центра масс до 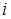 –й колеблющейся БТ; –й колеблющейся БТ; 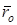 – математическое ожидание расстояния от РЛС до колеблющегося ЦМ. – математическое ожидание расстояния от РЛС до колеблющегося ЦМ.
Радиальные составляющие колебаний БТ с угловой скоростью будут определять изменения мгновенной доплеровской частоты. Доплеровская частота для 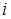 –й БТ при –й БТ при 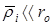 будет равна будет равна 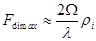 . .
Например, при движении цели на РЛС расстояние от 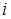 – й БТ до центра раскрыва антенны РЛС будет описываться выражением – й БТ до центра раскрыва антенны РЛС будет описываться выражением
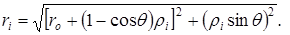 (1.5) (1.5)
При малых угловых высотах цели 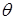 величиной величиной  можно пренебречь. Тогда можно пренебречь. Тогда 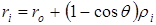 , а , а
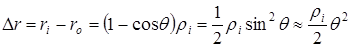 . (1.6) . (1.6)
Так как флуктуации фазы БТ определяют доплеровскую добавку
 
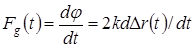
с учетом  окончательно запишем окончательно запишем
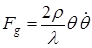 (1.7) (1.7)
Так, например, при 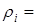 5 мм, 5 мм, 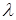 = 8 мм и = 8 мм и 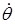 = 0,25 рад/с величина = 0,25 рад/с величина 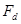 составляет 78 Гц. Видно, что с уменьшением составляет 78 Гц. Видно, что с уменьшением 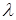 или увеличением или увеличением 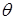 увеличивается доплеровская добавка. Кроме того, различия в скорости угловых колебаний (вибраций) увеличивается доплеровская добавка. Кроме того, различия в скорости угловых колебаний (вибраций) 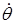 для различных целей являются основой для их распознавания. для различных целей являются основой для их распознавания.
Учитывая соотношения (1.5–1.7) рассмотрим фазовый множитель 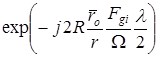 . Видно, что статистическая структура результирующего сигнала на входе антенны ИРТС будет определяться доплеровскими добавками . Видно, что статистическая структура результирующего сигнала на входе антенны ИРТС будет определяться доплеровскими добавками 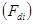 , вносимыми каждой блестящей точкой представляющей объект. Применяя сложные сигналы, позволяющие разделить блестящие точки цели (сверхразрешение по дальности или угловым координатам) и измеряя доплеровский сдвиг частоты для каждой из них, можно построить портрет цели в системе координат (линейный размер цели, доплеровская частота). Основой для решения задачи распознавания являются не только различия в числе БТ и расстояниях между ними для различных объектов, но и в особенностях их колебаний для движущейся цели или вибраций при нулевой скорости и работающем двигателе. Во всех указанных случаях проявляется эффект внешней когерентности (блуждания , вносимыми каждой блестящей точкой представляющей объект. Применяя сложные сигналы, позволяющие разделить блестящие точки цели (сверхразрешение по дальности или угловым координатам) и измеряя доплеровский сдвиг частоты для каждой из них, можно построить портрет цели в системе координат (линейный размер цели, доплеровская частота). Основой для решения задачи распознавания являются не только различия в числе БТ и расстояниях между ними для различных объектов, но и в особенностях их колебаний для движущейся цели или вибраций при нулевой скорости и работающем двигателе. Во всех указанных случаях проявляется эффект внешней когерентности (блуждания 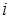 –й БТ относительно неподвижного или медленно колеблющегося ЦМ). Для когерентных РЛС, использующих узкополосные сигналы, этот эффект может быть зафиксирован в законе изменения максимумов допплеровского спектра коротких реализаций результирующего сигнала, а для некогерентных в определенной закономерности участков «сгущения» и «разрежения» диаграммы обратного рассеяния цели. –й БТ относительно неподвижного или медленно колеблющегося ЦМ). Для когерентных РЛС, использующих узкополосные сигналы, этот эффект может быть зафиксирован в законе изменения максимумов допплеровского спектра коротких реализаций результирующего сигнала, а для некогерентных в определенной закономерности участков «сгущения» и «разрежения» диаграммы обратного рассеяния цели.
В работе [79], автор которой для анализа статистической структуры сигналов, отраженных от цели, представляет ее совокупностью локальных отражателей показано, что двухмерная корреляционная функция для совокупности движущихся независимых отражателей равна
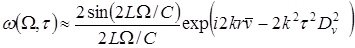 , (1.8) , (1.8)
где 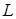 – линейный размер объема, занимаемого отражателями; – линейный размер объема, занимаемого отражателями; 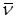 – средняя скорость их движения; – средняя скорость их движения; 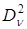 – дисперсия скорости. – дисперсия скорости.
Для совокупности жестко связанных отражателей эта зависимость имеет вид:
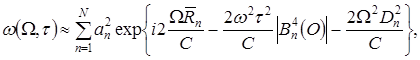 (1.9) (1.9)
где 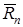 , , 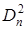 и и 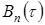 – среднее значение, дисперсия и корреляционная функция изменения расстояний до n– го отражателя во времени – среднее значение, дисперсия и корреляционная функция изменения расстояний до n– го отражателя во времени 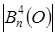 – дисперсия радиальной скорости n– го локального источника. Видно, что синхронность колебаний отражателей во втором случае приводит к зависимости функции – дисперсия радиальной скорости n– го локального источника. Видно, что синхронность колебаний отражателей во втором случае приводит к зависимости функции 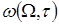 от числа отражателей и расстояний между ними. Степень жесткости связей отражающих элементов для автомобилей и танков различна, и это должно проявляться в статистической структуре фазы или доплеровского спектра отраженного сигнала, обусловленного особенностями колебаний конструктивных элементов целей. от числа отражателей и расстояний между ними. Степень жесткости связей отражающих элементов для автомобилей и танков различна, и это должно проявляться в статистической структуре фазы или доплеровского спектра отраженного сигнала, обусловленного особенностями колебаний конструктивных элементов целей.
1.2.2 Анализ современных методов спектрального оценивания мгновенного спектра
Из теории спектрального анализа известно, что существует два эквивалентных определения энергетического спектра (спектра мощности) сигнала [1]:
1. Квадрат модуля функции S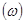
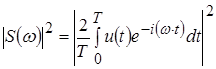 (1.10) (1.10)
2. Обратное преобразование Фурье автокорреляционной последовательности [1]:
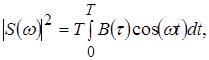 (1.11) (1.11)
Отметим, что вычисления, проведенные согласно (1.10) и (1.11) для сигналов, частота которых изменяется в широком интервале частот за время регистрации Т, позволяют констатировать наличие в спектре определенной гармоники, соответствующей данной частоте, но не позволяют зафиксировать, в какой момент времени появилась данная гармоника, поскольку вычисление спектра S(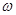 ) осуществляется интегрированием по всевозможным значениям переменной ) осуществляется интегрированием по всевозможным значениям переменной 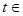 [0,T]. Осознание того факта, что спектр, определенный таким образом, не позволяет определить закон изменения частоты сигнала f=f(t), привело к созданию нового понятия цифрового спектрального анализа – понятию мгновенного спектра. На один из возможных способов введения этого понятия указывает (1.10). Проведем разбиение интервала регистрации [0,Т] на N подинтервалов, длиной T/N, что позволяет провести вычисление N значений функции Si
( [0,T]. Осознание того факта, что спектр, определенный таким образом, не позволяет определить закон изменения частоты сигнала f=f(t), привело к созданию нового понятия цифрового спектрального анализа – понятию мгновенного спектра. На один из возможных способов введения этого понятия указывает (1.10). Проведем разбиение интервала регистрации [0,Т] на N подинтервалов, длиной T/N, что позволяет провести вычисление N значений функции Si
(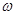 ) )
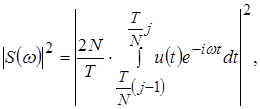 (1.12) (1.12)
где j = 1,..,N. Вычисленный набор S ((у) позволяет судить об эволюции спектра сигнала во времени. Данный подход к определению МС используется нами в дальнейшем. Отметим, что увеличение числа интервалов разбиения N приводит к необходимости вычисления спектров на реализациях сигнала малой длительности. Получение устойчивых (робастных) спектральных оценок, не обеспечиваемых классическими методами, требует применения неклассических методов спектрального оценивания, обсуждение которых проводится ниже.
Следует отметить, что исторически понятие МС было введено по аналогии с (1.11) как функция распределения мощности (энергии) p(t, f)
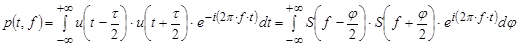 (1.13) (1.13)
С физической точки зрения функция 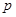 (t,f) определяет разность энергий двух бесконечно близких точек на плоскости (t,f). Полезно привести свойства функции (t,f) определяет разность энергий двух бесконечно близких точек на плоскости (t,f). Полезно привести свойства функции 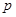 (t,f), которые поясняют ее физический смысл: (t,f), которые поясняют ее физический смысл:
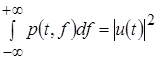 (1.14) (1.14)
то есть интеграл от функции p(t, f), взятый по частоте, определяет мощность (энергию) сигнала в данный момент времени.
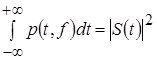 (1.15) (1.15)
то есть интеграл от функции p(t,f), взятый по времени, определяет спектральную плотность энергии на частоте f. Другие определения МС по Рихачеку, по Пейнджу, тесно связанные с функцией неопределенности, широко применяемой в импульсной радиолокации, можно найти в [11].
Проведем сравнение объема необходимых вычислений согласно (1.11) и (1.15). Предположим, что сигнал, значения амплитуды которого заданы в N точках, разбивается на k интервалов по N1
точек в каждом. Для вычисления спектра по (1.11), как правило, используется алгоритм БПФ [11]. Количество арифметических операций, при выполнении БПФ на N1
точках составляет N1
log2
N1
. Для нахождения МС по (1.14) необходимо провести вычисление автокорреляционной функции в N1
точках согласно (1.12). Вычисление одного значения автокорреляционной функции требует выполнения N1
операции умножения и N1
операции сложения. Следовательно, с учетом симметрии автокорреляционной функции, вычисление N1
, ее значений требует 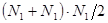 операций, последующее вычисление БПФ составляет операций, последующее вычисление БПФ составляет 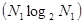 операций [12]. Таким образом, проведенная оценка свидетельствует, что первый способ требует меньшего количества арифметических операций, поэтому в дальнейшем для оценки мгновенных спектров используется (1.11). операций [12]. Таким образом, проведенная оценка свидетельствует, что первый способ требует меньшего количества арифметических операций, поэтому в дальнейшем для оценки мгновенных спектров используется (1.11).
Как очевидно, определение закона изменения частоты PC во времени будет тем более точным, чем меньше длительность интервала, на котором производится анализ PC. Уменьшение длины интервала, в свою очередь, проявляет основную проблему, стоящую перед цифровым спектральным анализом получение робастных оценок спектра и высокого частотного разрешения для последовательностей данных конечной (особенно малой) длительности. Два эквивалентных подхода к нахождению спектральной плотности мощности, основанных как на прямом ее вычислении по исходной последовательности данных (1.10), так и на Фурье–преобразовании автокорреляционной последовательности (1.11), позволяют оценить выборочные спектры, которые оказываются статистически несостоятельными, так как среднеквадратичная ошибка этих оценок сравнима по величине со средним значением оценки [11]. Поиски способов устранения отмеченного недостатка, активно проводившиеся в последнее десятилетие, привели к развитию нескольких методов спектрального оценивания, основанных на различных математических подходах: классических, параметрических, непараметрических.
К классическим методам относятся методы, основанные на прямом преобразовании Фурье данных с последующим усреднением по нескольким спектрам (периодограммные) и методы, основанные на оценке усредненной автокорреляционной последовательности исходных данных, получаемой Фурье–преобразованием (коррелограммные). При использовании классических методов оценивания спектра приходится принимать множество компромиссных решений с целью получения робастных спектральных оценок с максимально возможным разрешением. К таким решениям относятся выбор соответствующих функций окна для взвешивания данных и корреляционных функций и параметров усреднения во временной и частотной областях [19]. Устойчивые результаты и хорошая точность, под которыми понимаются малые спектральные флюктуации и незначительное смещение вычисленных значений спектра относительно его истинных значений на всех частотах, достигаются для сигналов, удовлетворяющих условию
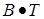 >>1, >>1,
где Т – время регистрации, В – разрешение по частоте [12]. Эти компромиссы теоретически обоснованы лишь для гауссовых случайных процессов. Рекомендации по выбору того или иного метода спектрального оценивания и функции окна в случае негауссовых случайных процессов, а также сигналов со сложным законом изменения частоты, к которым относится PC, получаемые при внутри–ствольных измерениях, отсутствуют. Подробную обширную информацию по классическим методам спектрального оценивания можно найти в [17–19,13–16]. Использование периодограммных и коррелограммных методов (понимаемых в смысле [17] для вычисления мгновенных спектров частотно–модулированных сигналов, к которым относятся PC, и возможности восстановления с их помощью закона изменения частоты сигнала, нам неизвестны. Отметим, что понятия периодиограммных и коррелограммных методов, применяемых нами для оценивания мгновенных спектров сигнала, созвучны с названиями корреляционных и ковариационных методов, используемых в работе [18], для спектрального оценивания на основе решетчатой структуры. Однако, суть их принципиально различна, так как в [18] они применяются только для оценивания корреляционной матрицы, использующейся в дальнейшем в параметрических методах спектрального оценивания (см. ниже), но не спектра сигнала.
Получение более точных оценок спектральных характеристик сигнала (по сравнению с достигаемыми с помощью классических методов) потенциально возможно при использовании параметрических методов. В данных методах исходная временная последовательность рассматривается как выходная последовательность каузального фильтра, на вход которого подается возбуждающая последовательность [16]. Модель временного ряда, пригодная для аппроксимации большинства детерминированных и стохастических сигналов с дискретным временем, описывается как
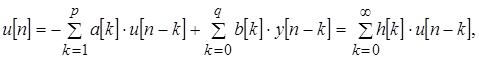 (1.16) (1.16)
где u[n] – последовательность на выходе каузального фильтра, y[n] – входная возбуждающая последовательность, h[k] – передаточная функция фильтра.
В зависимости от условий, накладываемых на коэффициенты, входящие в модель цифрового ряда, получают различные параметрические модели. Модель (1.16) в предположении, что последовательность у[п] является белым шумом имеет название модель авторегрессии – скользящего среднего (АРСС), здесь коэффициенты a[k] характеризуют авторегрессионую часть этой модели, а параметры b[k] – ее часть, соответствующую скользящему среднему. Если все коэффициенты a[k], называемые авторегрессиоными параметрами (АР–параметрами), за исключением а[0] равного единице, положить равными нулю, то тогда модель временного ряда принимает вид:
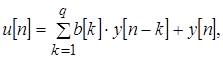 (1.17) (1.17)
модель становится строго процессом скользящего среднего порядка q (CC(q) –процессом).
Если все коэффициенты b[k], называемые параметрами скользящего среднего (СС – параметры), положить равными нулю, тогда модель временного ряда принимает вид:
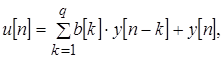 (1.18) (1.18)
модель становится чисто авторегрессионой моделью (АР–модель). Величины р и q – называются параметрами модели APCC(p,q) (р – параметр авторегрессионной модели, q – параметр скользящего среднего).
Из теории линейных систем [134] известна связь между линейной импульсной характеристикой h[k] и коэффициентами a[k], b[k], выражаемая через Z–преобразование. Последовательностям h[k], a[k], b[k] ставятся в соответствие функции H(z) (дискретная системная функция фильтра [32]), A(z), B(z) (Z– преобразование последовательностей a[k], b[k]), между которыми существует следующая связь
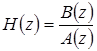 , (1.19) , (1.19)
где A(z), B(z), H(z) определяются как
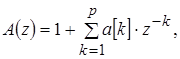 (1.20) (1.20)
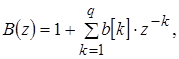 (1.21) (1.21)
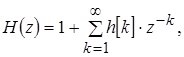 (1.22) (1.22)
здесь z – произвольное комплексное число.
Условием устойчивости данного каузального минимально–фазового фильтра является нахождение нулей полиномов A(z), B(z) внутри единичной окружности в Z–плоскости. Z–преобразование выходной автокорреляционной последовательности u[n] – Puu
(z) и Z–преобразование входной автокорреляционной последовательности случайного процесса y[n] – Pyy
(z) связаны следующим соотношением [5]
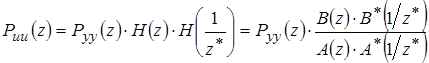 , (1.23) , (1.23)
где знак * означает комплексное сопряжение.
Предполагая, что входная последовательность является белым шумом с нулевым средним и дисперсией pw, так что pui^Pw, выражение (1.17) принимает вид:
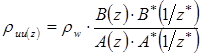 й(1.24) й(1.24)
Спектральную плотность мощности для АРСС(р,о)–модели получают из (1.24) заменой z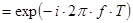 , которую масштабируют на длительность интервала Т , которую масштабируют на длительность интервала Т
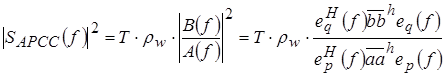 (1.25) (1.25)
где полиномы A(f), B(f) определяются выражениями:
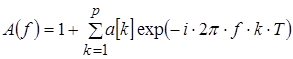 (1.26) (1.26)
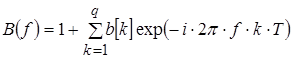 (1.27) (1.27)
векторы комплексных синусоид е (f),e (f) и векторы параметров a, b имеют вид:
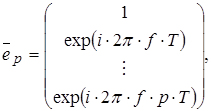 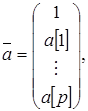
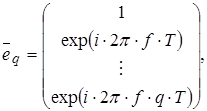 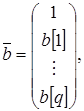 (1.28) (1.28)
знак Н означает операцию эрмитова сопряжения.
Полагая в (1.28) р равным нулю, получаем выражение для спектральной плотности мощности CC(q) – npoцecca
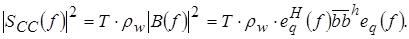 (1.29) (1.29)
Полагая в (1.25) q равным нулю, получаем выражение для спектральной плотности мощности АР(р)–процесса
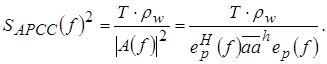 (1.30) (1.30)
Таким образом, как видно из (1.25), (1.29), (1.30) для оценки спектров необходимо вычисление параметров модели a[k], b[k] по известной автокорреляционной последовательности, что приводит к системе уравнений Юла–Уолкера для APCC(p,q), AP(p), СС(о)–процессов, для решения которой используют рекурсивные алгоритмы, связывающие АР–параметры более высокого порядка с параметрами более низкого порядка [31]. В связи с тем, что авторегрессионные спектры имеют более острые пики (это часто связано со спектральным разрешением) и уравнения Уюла–Уолкера для АР–процесса линейны, в отличие от APCC(p,q) и СС(о)–моделей, данное направление наиболее исследовано. Следует отметить, что свойства АР(р)–процесса и его спектра породили другие его названия – метод максимальной энтропии [25,26] и метод линейного предсказания [21,22]. Подход к трактовке коэффициентов a[k], b[k], как коэффициентов отражения при интерпретации измерений физических параметров акустической трубы [25,26] и сейсмических данных, получаемых при исследовании слоистой структуры Земли, привел к созданию популярного в настоящее время метода оценки АР–параметров по последовательности оценок коэффициентов отражения – алгоритм Берга [14,15]. Помимо алгоритма Берга в [13] рассмотрены другие алгоритмы оценки коэффициентов отражения – геометрический алгоритм, рекурсивное оценивание по методу максимального правдоподобия, предложенные в [14,15]. В основе их лежит предположение о том, что из всех коэффициентов отражения a[k] только коэффициент а[р], равный коэффициенту отражения, зависит от автокорреляционной функции.
Другой подход состоит в минимизации ошибки линейного предсказания методом наименьших квадратов по всем коэффициентам линейного предсказания. В зависимости от способа линейного предсказания различают алгоритмы с раздельным и комбинированным линейным предсказанием вперед и назад [13] – ковариационный и модифицированный ковариационный методы.
Основной трудностью реализации данных алгоритмов спектрального оценивания является неопределенность в выборе оптимального порядка фильтра. Поэтому решение о выборе того или иного порядка фильтра принимается заданием того или иного критерия ошибки, сравнением с которым определяется требуемый порядок модели. Малый порядок модели приводит к сильно сглаженным спектральным оценкам, излишне большой – к появлению ложных пиков. Следовательно, выбор порядка модели, определяющий разрешение спектра
и его дисперсию, эквивалентен выбору между разрешением и дисперсией для классических методов спектрального оценивания. Для выбора порядка модели предложено несколько критериев, подробно обсуждаемых в [14], поэтому ограничимся их кратким упоминанием:
1. Окончательная ошибка предсказания (ООП) (выбор порядка АР–процесса выбирается из требования минимизации средней дисперсии ошибки).
2. Информационный критерий Акаике (ИКА) (порядок модели определяется посредством минимизации некоторой теоретической информационной функции).
3. Авторегрессионный передаточной функции критерий (АПФК) (порядок модели выбирается равным порядку, при котором оценка разности среднего квадрата ошибки между истинным фильтром предсказания ошибки и оцениваемым фильтром минимальна).
Результаты оценивания спектра при использовании критериев ООП, ИКА, АПФК близки друг к другу в случае реальных данных. Однако в случае коротких записей данных ни один из критериев не обеспечивает удовлетворительных результатов [13]. Точного аналитического решения задачи о выборе порядка модели в настоящее время нет, поэтому необходимо проведение численных экспериментов с имитационным PC для выбора оптимального порядка модели.
Модель APCC(p,q) имеет больше степеней свободы, чем АР(р)–модель, что позволяет ожидать более адекватную передачу формы спектров. Однако основной сложностью данного метода является необходимость решения системы нелинейных уравнений, связывающих коэффициенты a[k], b[k] и автокорреляционную последовательность исходных данных. Методы решения нелинейных уравнений, основанные на интерационных алгоритмах, требуют большого количества вычислений, но самое главное, они зачастую могут не обеспечить сходимость к верному решению, поэтому были разработаны методы, основанные на методе наименьших квадратов, позволяющие провести линеаризацию системы уравнений и раздельно оценить АР-параметры, а затем СС-параметры.
Для оценки АР-параметров используется один из вариантов модифицированного уравнения Юла-Уолкера [16]. Так же неопределенным остается вопрос о выборе параметра модели, так как модификация ИКА, проведенная для АР-модели, проверена только для самых простых случаев.
Известен также метод моделирования выборочной последовательности данных в виде линейной комбинации экспоненциальных функций – метод Про–ни. то есть используется аппроксимация последовательных данных детерминированной экспоненциальной моделью [14]. Математически данный метод формулируется следующим образом. Пусть имеется N точечная последовательность данных и[1], u[N]. В методе Прони эта последовательность оценивается р–членной моделью комплексных экспонент:
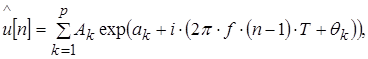 (1.31)
(1.31)
где 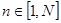 , , 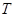 – время регистрации, – время регистрации, 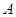 k
, k
,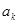 — амплитуда и коэффициент затухания k–ой комплексной экспоненты, — амплитуда и коэффициент затухания k–ой комплексной экспоненты,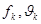 — частота и начальная фаза k–ой экспоненты. Функцию — частота и начальная фаза k–ой экспоненты. Функцию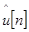 удобно представить в виде удобно представить в виде
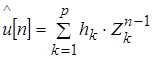 (1.32) (1.32)
где
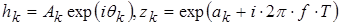 (1.33) (1.33)
Здесь hк
– комплексная амплитуда, независящая от времени, Zк
– комплексная экспонента, зависящая от времени.
Найдем квадрат ошибки интерполяции
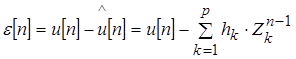 (1.34) (1.34)
Ошибку 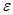 [n] минимизируют по параметрам hк
,zк
и числу компонент р. Если значение р неизвестно, то задача становится нелинейной. Решение нелинейной задачи требует применение метода Ньютона или метода градиентного спуска, которые наряду с большим объемом вычислений могут не обеспечивать сходимость к истинному решению. Эти трудности привели к разработке субоп–тимальных процедур минимизации, которые получили название – метод наименьших квадратов Прони [15]. Обычный метод наименьших квадратов Прони может быть модифицирован при использовании незатухающих комплексных синусоид ( [n] минимизируют по параметрам hк
,zк
и числу компонент р. Если значение р неизвестно, то задача становится нелинейной. Решение нелинейной задачи требует применение метода Ньютона или метода градиентного спуска, которые наряду с большим объемом вычислений могут не обеспечивать сходимость к истинному решению. Эти трудности привели к разработке субоп–тимальных процедур минимизации, которые получили название – метод наименьших квадратов Прони [15]. Обычный метод наименьших квадратов Прони может быть модифицирован при использовании незатухающих комплексных синусоид (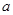 =0) [25]. Процедура Прони завершается вычислением оценок параметров, которые определяют амплитуду, коэффициент затухания, частоту и фазу. В [13] предложено определять спектр Прони в терминах экспоненциальной аппроксимации =0) [25]. Процедура Прони завершается вычислением оценок параметров, которые определяют амплитуду, коэффициент затухания, частоту и фазу. В [13] предложено определять спектр Прони в терминах экспоненциальной аппроксимации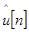 , а не в терминах временной последовательности u[n]. Спектральная плотность энергии Прони определяется как , а не в терминах временной последовательности u[n]. Спектральная плотность энергии Прони определяется как
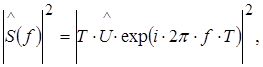 (1.35) (1.35)
где 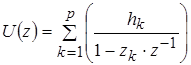 (1.36) (1.36)
для односторонней функции 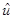 [n] (то есть, [n] (то есть, 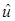 [n]=0 при n<0), [n]=0 при n<0),
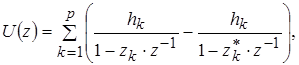 (1.37) (1.37)
для двусторонней функции 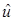 [n]. Известны приложения метода Прони к анализу динамики солнечных пятен и определения резонансных пиков в диаграммах эффективной площади рассеяния радиолокационных целей [12]. Исследования вопроса применимости данного метода к анализу ЧМ сигналов нам неизвестны. [n]. Известны приложения метода Прони к анализу динамики солнечных пятен и определения резонансных пиков в диаграммах эффективной площади рассеяния радиолокационных целей [12]. Исследования вопроса применимости данного метода к анализу ЧМ сигналов нам неизвестны.
К другому классу методов спектрального оценивания одномерных временных рядов относятся непараметрические методы – метод минимальной дисперсии (МД), и методы, основанные на гармоническом разложении Писаренко, – метод классификации множественных сигналов MUSIC (multipay signal classification) и метод оценки собственных векторов автокорреляционной матрицы или матрицы данных EV (eigenvector) [26].
Спектральная оценка, полученная методом МД, определяется выражением
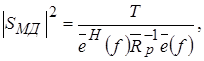 (1.38) (1.38)
где 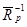 – матрица, обратная известной или оцененной автокорреляционной матрице – матрица, обратная известной или оцененной автокорреляционной матрице 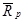 размером (р+1)х(р+1), размером (р+1)х(р+1),
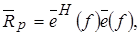 (1.39) (1.39)
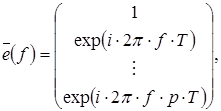 (1.40) (1.40)
Алгоритм метода МД и его программная реализация приведены в [14]. Следует отметить, что оценка спектральной мощности, получаемая согласно (1.30), не характеризует полную мощность измеряемого процесса, так как обратное преобразование Фурье спектральной оценки метода МД не соответствует истинной автокорреляционной функции. То есть спектральную оценку по методу МД можно считать спектральной в том смысле, что она описывает относительные интенсивности компонент частотного спектра, высота которых прямо пропорциональна мощности синусоид, присутствующих в исходном сигнале.
Этот класс методов спектрального оценивания основан на разделении информации, содержащейся в автокорреляционной матрице или матрице данных, на два векторных подпространства – подпространство сигнала и подпространство шума. Анализ собственных векторов матриц, относящихся к указанным
подпространствам, дает возможность определять различные функции от данных векторов, имеющие острые пики на частотах синусоид, присутствующих в исходном сигнале. Считается, что данные методы обеспечивают лучшее спектральное разрешение, чем АР-методы и метод Прони, особенно при низком отношении сигнал/шум [13].
Спектральная оценка при использовании собственных векторов подпространства сигнала получается из решения матричного уравнения
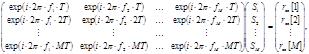 (1.41) (1.41)
относительно вектора неизвестных мощностей [14], любым известным методом решения линейных уравнений с комплексными коэффициентами.
Спектральная оценка методом MUSIC, основанным на использовании собственных векторов подпространства шума с равномерной весовой обработкой, определяется как
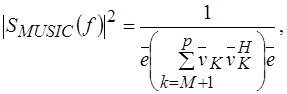 (1.42) (1.42)
где 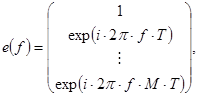 (1.43) (1.43)
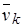 – собственный вектор подпространства шума. – собственный вектор подпространства шума.
Используя весовые множители 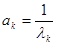 (где (где 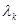 – собственное значение, соответствующее собственному вектору – собственное значение, соответствующее собственному вектору 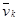 ), получаем алгоритм EV спектрального оценивания ), получаем алгоритм EV спектрального оценивания
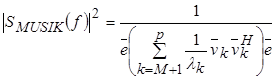 (1.44) (1.44)
Основным способом для принятия решения о значении числа М, соответствующего количеству собственных векторов подпространства сигнала, является анализ относительных величин собственных значений (сингулярных чисел) разложения автокорреляционной матрицы или матрицы данных по сингулярным значениям или использование модифицированного ИКА [14]. Следует отметить, что получаемая оценка, как и в методе МД, не является истиной спектральной плотностью мощности, так как обратное преобразование Фурье от (1.35), (1.36) не равно автокорреляционной последовательности. Исследования возможности применения непараметрических методов к анализу ЧМ сигналов, а также применимости данных методов и модифицированного ИКА при наличии небелого шума нам неизвестны.
В заключении обзора современных методов спектрального оценивания следует отметить, что проверка их частотного разрешения и статистической устойчивости выполнена либо на тестовых сигналах с известным составом (как правило, синусоиды плюс белый шум), либо для сигналов с медленно меняющимися параметрами (гидролокация, сейсмические сигналы, задачи пеленгации). Применительно к анализу сигналов с частотно–временными параметрами, аналогичными параметрам PC в задачах определения параметров поступательного движения снаряда в стволе, исследования ранее не проводились.
1.3 Поляризационные характеристики сигналов, отраженных от малоразмерных наземных целей при наличии помех от земной поверхности
В произвольном поляризационном базисе (ПБ) с эллиптически ортогональными ортами 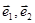 ЭМВ ЭМВ 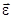 может быть единственным образом представлена как может быть единственным образом представлена как 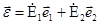 . .
Комплексные амплитуды 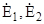 поляризационно–ортогональных компонент (ОПК) образуют вектор поляризации (ВП) [3]. поляризационно–ортогональных компонент (ОПК) образуют вектор поляризации (ВП) [3].
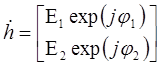 . (1.45) . (1.45)
Чисто поляризационные свойства ЭМВ могут быть описаны поляризационным отношением (фазовым) 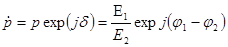 , причем , причем 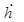 и и  изменяются при переходе к другому ПБ. изменяются при переходе к другому ПБ.
Инвариантными по отношению к пб являются поляризационные параметры (ПП):
- угол эллиптичности  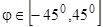 , знак которого соответствует направлению вращения вектора , знак которого соответствует направлению вращения вектора 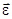 ; ;
- угол ориентации эллипса поляризации 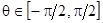 . .
В фиксированном ПБ между указанными ПП существуют известные однозначные взаимосвязи :
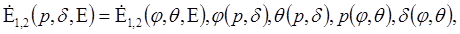 (1.46) (1.46)
где 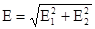 – полная амплитуда ЭМВ. – полная амплитуда ЭМВ.
Нормированный вектор поляризации ЭМВ и антенных систем
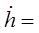 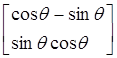  (1.47) (1.47)
определяет комплексную амплитуду принятого сигнала  , ,
где т–операция транспонирования; 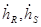 – ВП приемной антенны и ЭМВ. – ВП приемной антенны и ЭМВ.
Поляризационное состояние ЭМВ можно также описать вектором Стокса [12]
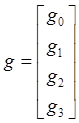 = = 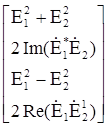 = = 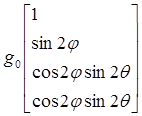 , (1.48) , (1.48)
где – 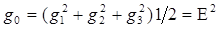 – полная мощность ЭМВ. – полная мощность ЭМВ.
Рассмотренные понятия являются математической основой для построения поляризационных моделей МНЦ.
1.3.1 Модели флуктуирующих наземных целей
Поляризационные характеристики (ПХ) МНЦ для заданного ПБ полностью описываются поляризационной матрицей рассеяния (ПМР)
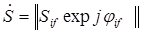 , i,j=1,2, (1.49) , i,j=1,2, (1.49)
причем для случая однопозиционной радиолокации 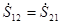 . ПМР однозначно определяет вектор поляризации . ПМР однозначно определяет вектор поляризации 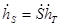 . .
Так как абсолютная фаза ПМР не влияет на поляризацию рассеянной ЭМВ и на мощность принимаемого сигнала, то без потери информации можно перейти к ПМР с относительной фазой или нормированной (по любому элементу) ПМР. В любом случае при заданной частоте зондирования и постоянном ракурсе наблюдения ПМР характеризуется пятью параметрами, четыре из которых носят сугубо поляризационный характер. В собственном ПБ объекта ПМР представляется через собственные числа
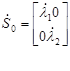 (1.50) (1.50)
К 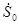 ,ПМР заданная в произвольном ПБ, может быть приведена при помощи унитарного преобразования ,ПМР заданная в произвольном ПБ, может быть приведена при помощи унитарного преобразования
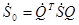 , ,
где
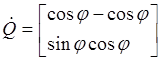 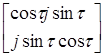 . .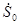 (1.51) (1.51)
Хьюненом  предложена форма представления собственных чисел предложена форма представления собственных чисел 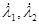 : :
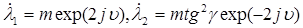 . (1.52) . (1.52)
В этом случае опять же МНО характеризуется пятью вещественными характеристиками, которым Хьюненом дана следующая физическая трактовка [12]:
m – «заметность или величина объекта», служит общей мерой размера МНЦ;
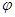 – «угол ориентации объекта», – «угол ориентации объекта», 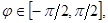 служит мерой ориентации объекта относительно линии визирования; служит мерой ориентации объекта относительно линии визирования;
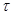 – «угол эллиптичности объекта», – «угол эллиптичности объекта»,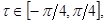 служит мерой симметрии объекта относительно правой и левой круговых поляризаций ( служит мерой симметрии объекта относительно правой и левой круговых поляризаций (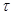 =450
– для симметричных объектов и =450
– для симметричных объектов и 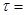 ±450
для полностью асимметричных); ±450
для полностью асимметричных);
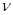 – «угол скольжения объекта», – «угол скольжения объекта»,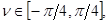 характеризует множественность переотражений сигнала от объекта (для однократного переотражения характеризует множественность переотражений сигнала от объекта (для однократного переотражения 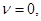 для двукратного – для двукратного –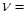 ±450
); ±450
);
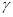 – «угол поляризации объекта», – «угол поляризации объекта»,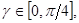 характеризующий способность объекта поляризовывать падающее на него неполяризованное излучение ( характеризующий способность объекта поляризовывать падающее на него неполяризованное излучение (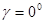 –для полностью поляризованного и –для полностью поляризованного и 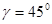 –для неполяризованного отраженных сигналов). –для неполяризованного отраженных сигналов).
Необходимо отметить, что в литературе [8] известны и другие формы представления матрицы Q:
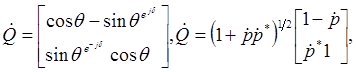 (1.53) (1.53)
где 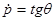 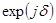 и и 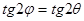 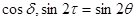 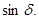
Инвариантами ПМР относительно ПБ являются:
- след ПМР (полная ЭПР МНЦ) А= 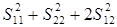 = =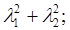
- детерминат ПМР В=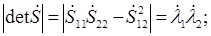
- степень поляризационной анизотропии
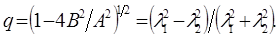
Таким образом, рассмотрены основные свойства ПМР и выявлены ее характеристики, которые могут использовать для описания ПХ МНЦ.
При наблюдении флуктуирующих МНЦ определенные выше параметры являются случайными, поэтому объект может быть охарактеризован многомерным законом распределения этих ПП. Применительно к задаче поляризационной селекции более конструктивные результаты получаются при рассмотрении введенной ранее матрицы М или ковариационной матрицы рассеяния R определяемой как
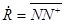 , ,
где
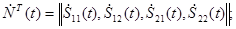
« + »– знак транспортирования и комплексного сопряжения. Матрица– столбец 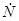 , ковариационная матрица R при переходе из линейного в новый ПБ подвергаются линейным преобразованиям , ковариационная матрица R при переходе из линейного в новый ПБ подвергаются линейным преобразованиям 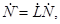 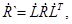 где L–унитарная матрица перехода. Матрица R имеет шесть независимых элементов: вещественные R11
, R22
, R33
и комплексные где L–унитарная матрица перехода. Матрица R имеет шесть независимых элементов: вещественные R11
, R22
, R33
и комплексные 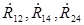 . Следовательно, матрица R имеет 9 независимых параметров. . Следовательно, матрица R имеет 9 независимых параметров.
Для описания ПХ МНЦ используются также матрицы когерентности отраженного сигнала, в заданном ПБ определяемая через усреднение по времени как
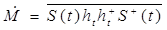 , (1.54) , (1.54)
где  –поляризационный вектор зондирующей ЭМВ. Матрица –поляризационный вектор зондирующей ЭМВ. Матрица 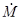 позволяет определить степень поляризации отраженного сигнала: позволяет определить степень поляризации отраженного сигнала:
m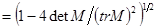 . .
Поток мощности отраженного сигнала определяется энергетической характеристикой рассеяния цели – матрицей Грейвса [4]:
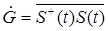 (1.55) (1.55)
Введенные в рассмотрение выше характеристики стабильных и флуктуирующих по поляризации объектов позволяют рассмотреть задачу разложения (декомпозиции) ПМР на несколько составляющих объектов. Такой подход обеспечивает проведение анализа эффективности различных методов поляризационной селекции и сравнительный анализ ПХ различных МНЦ.
Известно несколько декомпозиционных моделей, основанных на разложении матрицы вторых моментов или матрицы Мюллера произвольно флуктуирующего МНЦ на сумму не более трех матриц вторых моментов, соответствующих статистически независимым стабильным по поляризационным свойствам цели, или на сумму двух матриц, соответствующих стабильной и флуктуирующей (шумовой) целям.
1.3.2 Декомпозиционная поляризационная модель Хьюнена
Хьюненом доказана теорема о единственности разложения цели, на одиночный эффективный (стабильный по поляризации объект) с матрицей вторых моментов 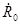 задаваемой пятью параметрами задаваемой пятью параметрами 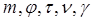 и шумовую компоненту и шумовую компоненту 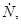 характеризуемую четырьмя параметрами, причем характеризуемую четырьмя параметрами, причем
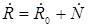 . (1.56) . (1.56)
Декомпозиция возможна не только средним мощностям сигналов но и к значениям
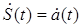 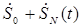 (1.57) (1.57)
где – 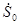 – матрица стабильной цели, соответствующая – матрица стабильной цели, соответствующая 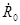 ; ;
- 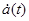 – комплексный скаляр с нормированным квадратом модуля – комплексный скаляр с нормированным квадратом модуля 
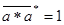 ; ;
- 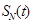 – ПМР «шумовой цели» со структурой – ПМР «шумовой цели» со структурой
-
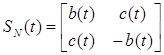 (1.58) (1.58)
Составляющие в (1.57) являются взаимно некоррелированными.
Достоинством данной модели является то, что шумовая матрица инвариантна к повороту системы в круговом ПБ от шумовой цели.
Недостаток же состоит в том, что параметры шумовой матрицы в общем случае не выражаются через инварианты эквивалентной стабильной ПМР.
1.3.3 Декомпозиционная поляризационная модель Джули
На основе (1.57) в работе [6] разработана модель объекта для поимпульсного представления отраженного сигнала. Рассматривая дискретно–временное представление матрицы S(t), где t=i*T (i–целое) и Т–период повторения импульсов. «Шумовая» матрица определяется как
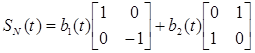 . (1.59) . (1.59)
Данная модель определяет характеристики процессов 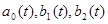 в моменты установившегося состояния адаптации антенны при посылках сигнала на один и тот же объект, но при различных импульсах. Полагается, что все рассматриваемые случайные последовательности являются локально – стационарными, гауссовыми с нулевым средним и некоррелированными действительной и мнимой частями. Последовательность в моменты установившегося состояния адаптации антенны при посылках сигнала на один и тот же объект, но при различных импульсах. Полагается, что все рассматриваемые случайные последовательности являются локально – стационарными, гауссовыми с нулевым средним и некоррелированными действительной и мнимой частями. Последовательность 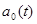 раскладывается как раскладывается как 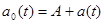 , где А – гауссова случайная величина с нулевым средним и дисперсией , где А – гауссова случайная величина с нулевым средним и дисперсией  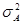 , которая постоянно в течении установившегося состояния антенны, , которая постоянно в течении установившегося состояния антенны,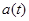 – последовательность белого шума, независящая от А; – последовательность белого шума, независящая от А; 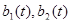 – последовательности белого шума с одинаковыми дисперсиями – последовательности белого шума с одинаковыми дисперсиями 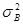 . .
Данная модель характеризуется 8 параметрами: пять описывают матрицу S0
и три дисперсии 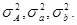 Вместо этих трех дисперсий можно использовать следующие параметры: Вместо этих трех дисперсий можно использовать следующие параметры:
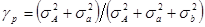 – степень поляризации; – степень поляризации;
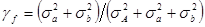 – величина флуктуации; – величина флуктуации;
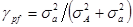 – величина флуктуации поляризации; – величина флуктуации поляризации;
Для описания ПХ некоторых типов мешающих отражений при численных оценках можно пользоваться упрощенной моделью «эффективной» матрицы S0
:
 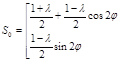 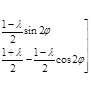 , (1.60) , (1.60)
где 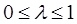 – отношение между минимальными и максимальными коэффициентами. – отношение между минимальными и максимальными коэффициентами.
1.4 Анализ методов поляризационной селекции наземных целей
1.4.1 Классификация методов поляризационной селекции
По принципу действия радиотехнические системы с поляризационной селекцией объектов можно разделить на следующие группы [21,22]:
- по количеству каналов приема: одноканальные и двухканальные (с приемом отраженных сигналов на двух ортогональных поляризациях);
- основанные на оптимизации ПП антенн: при излучении и приеме, только при излучении, только при приеме, при совпадении поляризациях излучения и приема;
- основанные на выборе постоянных ПП антенн и с управляемой поляризацией (адаптивные);
- когерентные и некогерентные;
- по типам зондирующих сигналов:
- монополяризованные при постоянных ПП антенн
- с использованием поляризационно – модулированных сигналов, для РЛС с непрерывным и импульсным излучением;
- по количеству антенн: с общей антенной на излучение и прием, и с различными передающей и приемной антеннами;
- ориентированные на типы помех: от подстилающей поверхности, гидрометров, дипольных отражателей, внутренних неполяризованных шумов, активных помех;
- с совмещением ПС с другими видами селекции;
- по критериям оптимизации: максимизация отношения сигнал / помеха, минимизация мощности помехи, оптимизация критерии теории статистических решений.
Изложенные факторы позволяют классифицировать известные методы поляризационной селекции. Результаты анализа представлены на рис. 1.5. Предложенная классификация может служить для рассмотрения известных методов по классификационным группам.

Рис. 1.5. Классификация методов поляризационной селекции
1.4.2 Методы с выбором постоянных ПП антенн при излучении и приёме
Для данной группы методов характерно использование нескольких подходов:
1) цель и помеха характеризуются стабильным ПМР;
2) цель и помеха являются флуктуирующими и описываются ковариационной матрицей рассеяния (КМР) или матрицей Мюллера.
При этом оптимизироваться могут ПП приёмной антенны при фиксированной поляризации на излучение, ПП передающей антенны, ПП передающей и приёмной антенны, ПП антенны, одинаковые на излучение и приём. Критерием оптимизации может являться максимизация ОСП и минимизация мощности помехи. Методы ПС, основанные на выборе постоянных ПП антенн при излучении и приёме детально рассмотрены в работах [7,11,13-15,30], анализ которых показал:
- использование в качестве моделей МНЦ стабильных ПМР цели и помехи малоприемлемо для радиолокационной практики;
- выражений, определяющих оптимальные поляризации излучения
и приёма для минимизации мощности флуктуирующей помехи,
в явном виде не получено;
- раздельная оптимизация поляризационных параметров антенн при излучении и приёме может приводить к потере эффективности селекции.
Таким образом, методы, основанные на выборе постоянных ПП антенн, малопригодны для практического использования, так как они основаны на предположении об известности и неизменности ПХ целей и помех, в то время, как ПХ реальных объектов и помех, как правило, неизвестны и изменчивы. Данные методы позволяют лишь частично использовать ПХ для селекции надводных объектов, как, например, применение круговой поляризации на излучение и приём для подавления помех от осадков. Однако эти методы характеризуют потенциальные возможности ПС при оптимизации ПП антенн, поэтому эффективность разрабатываемых методов ПС, пригодных для практической реализации, может оцениваться по сравнению с рассмотренными методами, а методика расчёта оптимальных поляризаций может облегчить синтез устройств ПС, эквивалентных методам с управляемыми ПП антенн.
1.4.3 Методы с двуканальным приёмным устройством
Известны методы ПС, основанные на излучении зондирующих сигналов с одной фиксированной поляризацией и обработке двух ортогонально поляризованных компонент (ОПК) отражённого сигнала [3,4]. Неадаптивные двухканальные методы основываются на некогерентном объединении сигналов двух каналов, для селекции используются различия в статистике двух целей, устанавливаемые по выборкам отражённых сигналов путём усреднения их параметров.
Так, например, система, имеющая фиксированную круговую поляризацию при передаче и двухканальное приёмное устройство в качестве средства уменьшения потерь мощности сигнала, отражённого от цели, в секторах, свободных от осадков, [18] позволяет получить выигрыш при обнаружении до 4 дБ по сравнению со случаем излучения и приёма линейной поляризации (традиционный случай) за счёт суммирования мощности выборочных статистик, определяемых последетекторным интегрированием. Объединение огибающих основной и кроссовых компонент ОПК отражённого сигнала [19] с оптимальным весовым коэффициентом позволяет повысить качество обнаружения малоконтрастной точечной цели на фоне подстилающей поверхности. Улучшение в ОСП по сравнению с одноканальным методом может достигать при этом 5…15 дБ в зависимости от различий степени деполяризации цели и помехи и коэффициентов корреляции между ОПК, которые на практике могут быть неизвестны, так как различны для различных целей и типов подстилающей поверхности. Таким образом, в качестве одного из направлений дальнейших исследований целесообразно принять принцип двухканального приёма ОПК отражённых сигналов с их последующей весовой обработкой.
В работе Лонга [20] описано устройство подавления помех от земной и морской поверхности, также использующее различия огибающих отражённых сигналов, принятых по двум ортогональным каналам. Принцип действия устройства основывается на том, что для поляризационно–изотропных целей отношение основных элементов ПМР в линейном ПБ близко к единице, а для выборок помехи от земной поверхности или близко к нулю, или много больше единицы. Устройство содержит два видеоканала раздельного приёма горизонтальной и вертикальной ОПК. Их сигналы подаются на входы сумматора и компаратора, выходные сигналы которых управляют вентилем. Сигнал с выхода устройства выдаётся только в случае, если амплитудное соотношение ОПК близко к единице. Зондирующий сигнал ориентирован под 450
по отношению к ПБ приёмной антенны. Фазовые различия ПМР цели и помехи не используются, поскольку предполагаются неизвестными. Данный подход также относится к некогерентным методам. Целесообразно в дальнейшем рассмотреть возможности некогерентных методов поляризационной селекции.
В [7] предложен метод обработки, использующий различия в когерентности цели и помехи, которая проявляется во временной когерентности разности фаз одновременно принимаемых ОПК (рис. 1.6). Цели выделяются на фоне МО, если за период наблюдения фазовый сдвиг более или менее постоянен для МО и изменяется для сигналов от цели. Эффективность данного метода экспериментально не оценивалась. Структура такой системы (рис. 1.6) аналогична системам с череспериодной компенсацией в системах СДЦ. А в работе [23] показано, что одновременная обработка двух ортогонально – поляризованных сигналов позволяет улучшить разрешение целей по частоте Доплера. Таким образом, предполагается целесообразным рассмотреть в дальнейшем возможность совмещения поляризационной и доплеровской селекций.

Рис. 1.6. Структура поляризационного выделителя сигналов
1.4.4 Методы ПС с использованием поляризационной модуляции зондирующего сигнала
Известны [4] методы с использованием так называемого поляризационного сканирования, при котором поляризация антенн (на передачу и приём) периодически изменяется по определенному закону. При облучении цели на фиксированной поляризации в отраженном сигнале содержится информация только об одном элементе главной диагонали ПМР, использование поляризационного сканирования позволяет повысить качество информации. Например [4], если поляризация антенны (общая на передачу и прием) периодически изменяется так, что точка на сфере Пуанкаре, соответствующая поляризации антенны движется по окружности большого круга (плоскость поляризации вращается с частотой 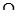 ), то на выходе приемной антенны интенсивность отраженного сигнала имеет вид: ), то на выходе приемной антенны интенсивность отраженного сигнала имеет вид:
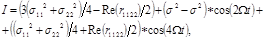 (1.89) (1.89)
откуда следует, что амплитуды спектральных компонент содержат информацию об элементах главной диагонали ПМР (дисперсии 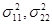 , вещественной части взаимного коэффициента корреляции , вещественной части взаимного коэффициента корреляции 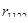 ). Если помеха изотропна ). Если помеха изотропна 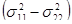 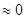 , а цель неизотропна, то использование гармонической компоненты , а цель неизотропна, то использование гармонической компоненты 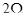 позволяет селектировать неизотропные цели на фоне изотропной помехи. Рассмотренный выше метод впервые был предложен в [22] для селекции целей на фоне взволнованной морской поверхности. Следует отметить противоречие метода Лонга, рассмотренного в [12], и метода поляризационного сканирования [22] для селекции целей на фоне подстилающей поверхности. Лонг исходит из того, что цели изотропны, а поверхность – нет, а использование метода поляризационного сканирования основано на противоположном предположении. позволяет селектировать неизотропные цели на фоне изотропной помехи. Рассмотренный выше метод впервые был предложен в [22] для селекции целей на фоне взволнованной морской поверхности. Следует отметить противоречие метода Лонга, рассмотренного в [12], и метода поляризационного сканирования [22] для селекции целей на фоне подстилающей поверхности. Лонг исходит из того, что цели изотропны, а поверхность – нет, а использование метода поляризационного сканирования основано на противоположном предположении.
Известен ряд методов, основанных на двухпозиционной поляризационной манипуляции с приемом на антенну, ПП которой совпадает с ПП на излучение. Эти методы позволяют ограничиться одноканальным приёмным устройством. В [24] показано, что для выделения сигналов, отраженных от целей на фоне помех, можно использовать как череспериодную поляризационную манипуляцию, так и внутриимпульсную поляризационную манипуляцию при соответствующей одноканальной обработке импульсных сигналов. Эффективность селекции зависит от того, насколько удачно выбраны поляризации излучения и приема РЛС, которые могут уточняться с увеличением экспериментальных данных. Достоинством данных методов является то, что возможность селекции появляется при ограниченных априорных данных о ПХ целей и помех, так как для обработки могут использоваться огибающие двух принятых сигналов при неизвестных фазах.
В работе [25] показано, что переключение поляризации при излучении (линейная – круговая) дает возможность селектировать МНЦ по их коэффициенту поляризационной анизотропии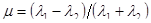 , который является инвариантным к преобразованию ПБ. Данный метод пригоден для случаев описания ПХ МНЦ упрощенной ПМР (1.54) без учета угла переотражения , который является инвариантным к преобразованию ПБ. Данный метод пригоден для случаев описания ПХ МНЦ упрощенной ПМР (1.54) без учета угла переотражения 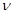 и угла спиралевидности и угла спиралевидности 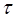 . .
Использование принципа поочередного излучения линейных ОПК в сочетании с синхронным двухканальным приемом позволяет использовать при обработке все элементы ПМР. Для получения алгоритма обработки при этом используют ПХ целей и помех, полученные путем усреднения на больших интервалах времени.
Управление поляризацией сигнала дает возможность использовать поляризацию в качестве зависимой от времени переменной для синтеза излучаемого сигнала. В этом случае и синтез сигнала и согласованная фильтрация для сжатия импульса должны рассматриваться как задача оптимизации алгоритма обработки векторного процесса. Такой подход может быть использован для улучшения разрешения целей на фоне МО. Возможности этого подхода исследовались с помощью РЛС с внутриимпульсной перестройкой поляризации [27]. Поляризационное кодирование сигнала осуществлялось посредством перехода от одной круговой поляризации (правой и левой) к другой на каждом элементарном импульсе в соответствии с кодовой последовательностью Баркера. Экспериментальная проверка [27] методов поляризационного кодирования показала, что расчетное сжатие импульсного сигнала достижимо на практике, возможна селекция одиночных простых целей.
Все перечисленные выше методы основываются на том, что априорно известны ПХ цели и помехи. Двухканальные методы хотя и могут требовать ограниченной априорной информации, не могут быть достаточно эффективны вследствие изменчивости ПХ от ракурса МНЦ, частоты сигнала, угла наблюдения, среды распространения и т. д., поэтому эффективность ПС на основе долговременных ПХ целей и помех не может быть значительной. В то же время, как показано в [27], за короткие промежутки времени, в течение которых освещается цель, отраженная волна, как правило, сохраняет постоянство поляризации. Кроме того, кратковременные ПХ целей и помех, особенно в сантиметровом и миллиметровом диапазоне электромагнитных волн, резко различны: у последних они менее изменчивы, а у пространственных помех (осадки, дипольные отражатели) и вообще однородны. Все это указывает на целесообразность применения адаптивной поляризационной селекции.
1.4.5 Адаптивные методы ПС
Методы, основанные на применении адаптации при приеме, проще всего реализовать при адаптивной обработке двух сигналов, принятых по двум ортогонально – поляризованным каналам. Линейно и когерентно объединяя два принятых сигнала, можно получить любое число поляризации без потерь мощности принимаемого сигнала. Адаптация поляризации при приеме чаще всего рассматривается как задача адаптивно-поляризационного подавления возмущений с определенной поляризацией.
Процедура подавления помех в РЛС с двойной поляризацией (двухканальный прием ортогонально–поляризованных сигналов) состоит в линейном объединении двух принятых сигналов 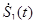 и и  и выборе весовых коэффициентов таким образом, чтобы подавлялись составляющие с определенной поляризацией. и выборе весовых коэффициентов таким образом, чтобы подавлялись составляющие с определенной поляризацией.
В работе [28] показано, что целесообразно использовать не оптимальную, но тем не менее достаточно эффективную процедуру
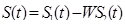 , , 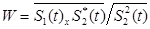 . (1.90) . (1.90)
Схема, реализующая данный алгоритм, показана на рис. 1.7. Результаты экспериментальных исследований адаптивного поляризационного подавления помех от осадков и преднамеренных помех при излучении круговой поляризации подтверждают эффективность такой обработки [29].
Дополнительное улучшение в ОСП по сравнению со случаем применения круговой поляризации для подавления МО от осадков при одноканальном приеме составляет 9дБ. ПХ помех могут быть адаптивно оценены по наблюдаемому сигналу, если они локально стационарны и равномерно распределены во времени и в пространстве.

Рис. 1.7. Структурная схема двухканального автокомпенсатора
В случае однородных по пространству МО, т.е. помех от гидрометеоров, отражений от морской поверхности, при некоторых типах МО от земли, и помех, создаваемых облаком диполей, можно за период наблюдения извлечь полезную информацию из степени поляризационной корреляции между различными пространственными ячейками, содержащими МО. В случае неоднородных МО необходимо отдельно определить поляризационный минимум для каждой ячейки путем измерения и запоминания данных. Так как каждая ячейка может содержать цель, метод подавления эффективен в том единственном случае, когда ПХ МО медленно изменяются от обзора к обзору. В работе [30] анализируются характеристики МО от земной поверхности. Отмечается, что в одном и том же окне от одного сканирования до другого наблюдается высокая стационарность ПХ. Отмечались существенные различия ПХ МНЦ и МО от земной поверхности.
Поскольку принятый сигнал активных помех не зависит от поляризации сигнала, излучаемого РЛС, их подавление требует применения поляризационной адаптации только при приеме.
Для МО степень поляризации отраженного сигнала, в общем случае, зависит от поляризации на излучение. Эффективность подавления помех при приеме зависит не только от ПП передающей антенны, но и от того, насколько различны ПХ МНЦ и МО. При излучении фиксированной поляризации и двухканальном адаптивном подавлении МО, сигнал от цели может быть в значительной степени ослаблен, даже если ПХ цели и помех различны. Следовательно, необходима адаптация ПП как передающей так и приемной антенн. Поляризационная адаптация при передаче может быть осуществлена за счет перестройки поляризации от одного излучаемого импульса к другому. Однако в большинстве случаев такое решение неприемлемо, поскольку требует значительного времени адаптации. Одно из эффективных решений данной проблемы дает метод последовательного излучения импульсов с двумя ортогональными поляризациями при полном поляризационном приеме каждого отраженного импульса (рис. 1.8). Если принять допущение о стационарности свойств МО, то такой режим работы позволяет синтезировать любую поляризацию излучения и приема посредством весовой обработки двух последовательных отраженных сигналов, благодаря этому методу подавление помех может быть построено на двухшаговой процедуре [7]:

Рис. 1.8. Устройство для синтеза произвольных поляризаций излучения и приема
1) при передаче выбрать поляризацию антенны, которая минимизирует среднюю мощность, содержащуюся в полностью неполяризованной компоненте сигнала МО;
2) при приеме установить поляризацию антенны, которая минимизирует среднюю мощность сигнала помехи.
Недостатком данного метода является то, что подавление помех не обязательно приводит к максимальному значению ОСП. Кроме того, не найдены процедуры обработки, пригодные для работы в реальном масштабе времени.
Методы, основанные на последовательном излучении двух ортогональных поляризаций при двухканальном приеме подвержены влиянию доплеровского сдвига, что может ухудшить эффективность ПС, и пригодны для РЛС с импульсным режимом излучения, поэтому целесообразен поиск методов, позволяющих одновременно выделять ПМР как для РЛС с импульсным, так и непрерывным режимом излучения.
Подавление МО с помощью одного поляризационного заграждающего фильтра является процессом с острой настройкой, характерной для любого нулевого метода, при этом эффективность подавления МО падает от ячейки к ячейке в объеме разрешения при обзоре, несовершенства разделения ОПК и т.д.
Для решения этой проблемы предложено устройство нового составного многополосного поляризационного фильтра [31]. Этот фильтр позволяет конструктивно управлять местоположением, глубиной и размером области подавления МО. При современной технологии реализация многополосного поляризационного фильтра, работающего в реальном масштабе времени и охватывающего умеренную область в поляризационном пространстве, возможна только в виде довольно громоздкого устройства, что привело к разработке концепции нелинейного поляризационно–векторного преобразования, которое позволяет значительно уменьшить количество полос фильтра без значительного снижения эффективности обработки в целом [32].
Таким образом, адаптивные методы ПС являются наиболее перспективными и могут быть осуществлены за счет быстрого управления поляризацией при приеме или при управлении поляризацией излучения и приема. Адаптацию поляризации на передачу целесообразно свести к адаптации при приеме за счет излучения нескольких фиксированных поляризаций одновременно или разнесенных во времени. Это целесообразно по двум причинам:
- перестройка поляризации излучения от одного импульса к другому неприемлема из–за большого времени адаптации;
- излучение одной фиксированной поляризации при приеме полном поляризационном приеме не позволяет полностью оценить ПХ МО.
2. Математическая модель реализуемой системы
2.1 Функции программного обеспечения
Программное обеспечение обрабатывающей ЭВМ представляло собой командно–мониторинговую интерактивную систему, выполняющую следующие функции:
– визуализация состояния программных и технических средств;
– прием, интерпретация и обработка команд оператора;
– прием данных от измерительно–управляющей ЭВМ, их размещение в памяти;
– запись данных на магнитные носители;
– обработка данных для извлечения поляриметрической и спектральной информации;
– графическая визуализация результатов измерений;
– предварительная статистическая обработка результатов измерений (расчет статистических характеристик параметров, построение гистограмм, корреляционный и спектральный анализ);
– графическая визуализация результатов обработки;
– поддержка электронного протокола измерений с автоматической регистрацией номера измерений, дальности до объекта, даты и времени измерения, полной характеристики режима измерений;
– поддержка электронной записной книжки оператора для регистрации особенностей измерений, метеоусловий и др. комментариев.
Рассчитанные ПМР являлись основой для определения поляризационных характеристик объектов.
При обработке результатов измерений определялись:
– коэффициент деполяризации 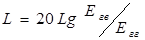 ; ;
– коэффициент асимметрии  ; ;
– параметр 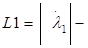 мера заметности цели ((L1)2
– максимум ЭПР цели для оптимальной поляризации). При Sгв
=Sвг
(используется одна приемопередающая антенна) λ1
определяется из соотношения мера заметности цели ((L1)2
– максимум ЭПР цели для оптимальной поляризации). При Sгв
=Sвг
(используется одна приемопередающая антенна) λ1
определяется из соотношения
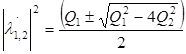 , (2.1) , (2.1)
где 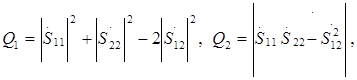 при ê при ê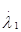 ÷> ê ÷> ê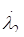 ÷; ÷;
– коэффициент анизотропии 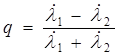 ; (2.2) ; (2.2)
– дескриптор Gam=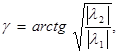 0 £ g £ 45о
γ – "угол поляризации, характеристический угол"; 0 £ g £ 45о
γ – "угол поляризации, характеристический угол";
– τm
– мера несимметричности цели или угол спиралевидности, определяемый из выражения: 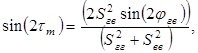 при этом –45о
£ tm
£ 45о
. Угол tm
также является углом эллиптичности максимальной поляризации m. при этом –45о
£ tm
£ 45о
. Угол tm
также является углом эллиптичности максимальной поляризации m.
– угол ориентации цели y или Psi
– угол наклона оси эллипса первой собственной поляризации; может быть рассчитан из выражения:
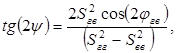 –90о
£ y £ 90о
, (2.3) –90о
£ y £ 90о
, (2.3)
– комплексный параметр 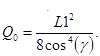 (2.4) (2.4)
Рассчитанные поляризационные параметры подвергались статистической обработке в соответствии с методикой обработки экспериментальных данных, включающей следующие этапы:
1. Расчет статистических характеристик параметров по ансамблю реализаций;
2. Построение экспериментальных гистограмм WN
(K) и FN
(K) и аппроксимация их выбранным теоретическим распределением, где K – анализируемый параметр;
3. Вычисление оценок параметров аппроксимирующего закона и определение закона их распределения.
Применительно к данной методике был разработан алгоритм статистической обработки экспериментальных данных.
К статистическим характеристикам параметров следует отнести численные характеристики случайного процесса E(t) за время наблюдения T, который при обработке преобразуется в дискретную последовательность E1
, E2
, …, EN
с шагом дискретизации Δt. Эти характеристики вычислялись по формулам:
  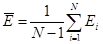 , (2.5) , (2.5)
где N=T/Δt – объем выборки, 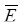 – среднее значение процесса (параметра) E(t); – среднее значение процесса (параметра) E(t);
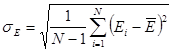 , (2.6) , (2.6)
где 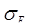 – среднеквадратическое отклонение процесса (параметра) E(t) от среднего значения – среднеквадратическое отклонение процесса (параметра) E(t) от среднего значения 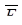 ; ;
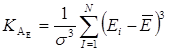 , (2.7) , (2.7)
где 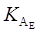 – коэффициент асимметрии; – коэффициент асимметрии;
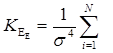 , (2.8) , (2.8)
где 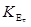 – коэффициент эксцесса. – коэффициент эксцесса.
Коэффициенты 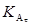 и и 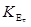 характеризуют отличие случайного процесса (параметра) E(t) от гауссовского, для которого характеризуют отличие случайного процесса (параметра) E(t) от гауссовского, для которого 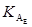 =0, =0, 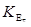 =3. =3.
Для оценки глубины флуктуаций процесса вычислялся коэффициент вариаций
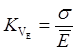 , (2.9) , (2.9)
Стандартные ошибки определения числовых характеристик могут быть оценены по формулам
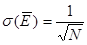 , (2.10) , (2.10)
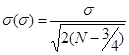 ; (2.11) ; (2.11)
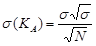 . (2.12) . (2.12)
Следовательно, при достаточно большом объеме выборки N этими ошибками можно пренебречь.
Рассмотренные числовые характеристики характеризуют форму кривой плотности распределения вероятностей ПРВ огибающей E(t) или огибающей рассчитанных параметров во временной области E(K) – WN
(E) или WN
(K). Экспериментальные гистограммы WN
(E) строились на основе обработки экспериментальных выборок E1
, E2
, EN
.
Затем эти гистограммы аппроксимировались теоретическим распределением W(E) (W(K)), которое наиболее полно описывает особенности флуктуаций огибающих сигналов, отраженных от наземных целей и подстилающих поверхностей, и поляризационных параметров объектов локации.
Методика аппроксимации гистограмм заключалась в следующем:
1. По вычисленным коэффициентам асимметрии и эксцесса проверялась возможность попадания точки с координатами 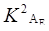 , ,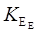 в область аппроксимирующего распределения [29]; в область аппроксимирующего распределения [29];
2. Проверяется согласование выбранного теоретического распределения с экспериментальным рядом по критериям согласия Колмогорова–Смирнова, χ2
и критерию ω2
[28].
Таким образом, для решения задач селекции наземных целей на фоне подстилающей поверхности и распознавания классов МНЦ необходимо получение достаточного статистического материала по структуре параметров отраженного сигнала и поляризационных параметров, на основе которых могут быть определены информативные признаки. Для решения указанной задачи определена номенклатура определяемых и рассчитываемых поляризационных параметров, разработана методика обработки экспериментальных данных и программное обеспечение, реализующее алгоритмы обработки.
При обработке экспериментальных данных алгоритм вычислений предусматривал определение статистических характеристик и законов распределения огибающих отраженных сигналов и поляризационных параметров.
2.2 Анализ спектральных характеристик движущихся МНЦ
и подстилающей поверхности
Подвергались анализу временные реализации сигналов, отраженных от движущихся наземных целей. В качестве колесной техники использовался автомобиль ЗИЛ-131, в качестве гусеничной – танки Т–Т2, Т–80, МТЛБУ «Пантера», 2С23 «Нона», САУ 2С3М «Акация». Спектральный анализ производился методом ДПФ, при этом время наблюдения процесса составляло Тн
= 0,9 с, интервал дискретизации Δt = 10–4
c. интервал дискретизации позволяет осуществлять анализ спектральных компонент до FB
= 5 кГц
. Для уменьшения влияния нестационарности процесса на вид и точность спектральных оценок применялось деление временных реализаций на равные части с последующим усреднением по частоте. Входным процессом для спектрального анализа являлись амплитудная и квадратурная составляющие основной компоненты горизонтального канала РЛС. Тн
= 0,9 с, интервал дискретизации Δt = 10–4
c. интервал дискретизации позволяет осуществлять анализ спектральных компонент до FB
= 5 кГц
. Для уменьшения влияния нестационарности процесса на вид и точность спектральных оценок применялось деление временных реализаций на равные части с последующим усреднением по частоте. Входным процессом для спектрального анализа являлись амплитудная и квадратурная составляющие основной компоненты горизонтального канала РЛС.
В качестве иллюстрации вид полученных спектральных оценок представлен на рис. 2.6–2.12. Полностью полученные спектральные оценки приведены в приложении 1. Анализ оценок позволяет сделать следующие выводы:
1. Амплитудный спектр сигнала, отражённого от разрешаемого РЛС участка поверхности, имеет fB
до частоты (50 ч 60) Гц и, следовательно, пересекается с основными составляющими амплитудного спектра целей.
2. Амплитудные спектры классов гусеничной и колёсной техники достаточно сильно пересекаются. По виду наблюдаемого спектра невозможно сделать однозначный вывод о принадлежности объекта определённому классу Ω
i
,
i
=
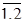 .
.
3. На точность оценки спектральной плотности мощности отражённого сигнала существенно влияет наличие отражений от участка подстилающей поверхности (вместе с растительностью), свободного от цели, в пределах стробируемого элемента дальности.
Действительно, при τu
= 0,1 μс, размер участка дальности составляет ΔД = 15 м, тогда как максимальный размер цели lц
= 6–7 м. Указанное обстоятельство приводит к увеличению ошибок определения величины спектральных составляющих и, в конечном счёте, к росту ошибок классификации целей.
По полученным оценкам спектра были рассчитаны некоторые спектральные параметры целей, предложенные на ранних этапах работы [18,19], часть из них приведена в таблицах 2.1–2.8. В качестве спектральных признаков рассматривались: положение первого FGmax
1
и второго FGmax
2
максимумов спектральной плотности на частотной оси, ширина спектра по уровню 0,5 – ΔF0,5
для этих максимумов, значение первого спектрального момента
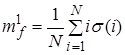 , (2.13) , (2.13)
коэффициенты формы спектра
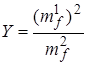 , где (2.14) , где (2.14)
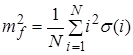 , (2.15) , (2.15)
значение энергии сигнала
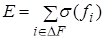 , (2.16) , (2.16)
коэффициент вариации спектра
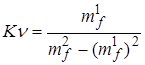 . (2.17) . (2.17)
Амплитудный спектр сигнала отраженного от объекта
Рис. 2.6. Амплитудный спектр сигала отражённого от Т 80
 Рис. 2.7. Амплитудный спектр сигала отражённого от Т 72
Рис. 2.8. Амплитудный спектр сигала отражённого от РЛС «Пантера»
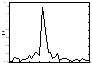
Рис. 2.8. Амплитудный спектр сигала отражённого от САУ
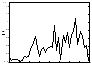 Рис. 2.8. Амплитудный спектр сигала отражённого от ЗИЛ 131
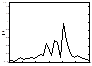
Рис. 2.8. Амплитудный спектр сигала отражённого от ЗИЛ 131
Спектр квадратурной компоненты сигнала отраженного от объекта

Рис. 2.9. ЗИЛ 131, бортовой, лобовая проекция, ПП – сухая трава, мелкий кустарник, файл 00.sig.

Рис. 2.10. ЗИЛ 131, бортовой, лобовая проекция, ПП – сухая трава, мелкий кустарник, файл 02.sig.
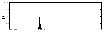
Рис. 2.11. Танк T 80, лобовая проекция, ПП – сухая трава, мелкий кустарник, файл 00.sig.
Рис. 2.12. Танк T 80, лобовая проекция,ПП – сухая трава, мелкий кустарник, файл 01.sig.

Рис. 2.13. Нона, лобовая проекция, ПП – сухая трава, мелкий кустарник, файл 01.sig.

Рис. 2.14. Пантера, лобовая проекция, ПП – мокрая трава, мелкий кустарник, файл 00.sig.

Рис. 2.15. T 72, лобовая проекция, ПП – сухая трава, мелкий кустарник, файл 00.sig.

Рис. 2.16. T 72, лобовая проекция,ПП – сухая трава, мелкий кустарник, файл 02.sig.

Рис. 2.17., подстилающая поверхность (ПП) – сухая трава, мелкий кустарник, файл 01.sig.
Результаты анализа амплитудного спектра
Таблица 2.1. Численные значения спектральных параметров для ЗИЛ 131.
| Объeкты и файлы
|
FGmax1 Гц
|
FGmax2 Гц
|
FI0,5 Гц
|
FII0,5 Гц
|
m1f
|
m2f
|
Y
|
Kvf
|
Ef
|
| ЗиЛ– 131
|
00.sig
|
0
|
7,49
|
2,54
|
8,56
|
1,66524
|
568,44
|
0,00488
|
0,002944
|
20,427
|
| 01.sig
|
0
|
5,35
|
2,1
|
4,28
|
1,63897
|
551,65
|
0,00487
|
0,002986
|
12,667
|
| 02.sig
|
0
|
3,21
|
2,16
|
8,56
|
2,24966
|
785,91
|
0,00644
|
0,002881
|
25,433
|
| 03.sig
|
0
|
3,21
|
2,4
|
6,42
|
2,64904
|
894,1
|
0,00785
|
0,002986
|
10,7
|
| 04.sig
|
0
|
8,56
|
2,42
|
4,28
|
1,81109
|
641,04
|
0,00512
|
0,00284
|
15,66
|
| 05.sig
|
0
|
4,28
|
2,18
|
6,42
|
1,98954
|
669,74
|
0,00591
|
0,002988
|
26,062
|
| 06.sig
|
0
|
3,21
|
2,9
|
6,42
|
2,00248
|
689,33
|
0,00582
|
0,002922
|
18,79
|
| 07.sig
|
0
|
3,21
|
2,5
|
6,42
|
1,54147
|
524,83
|
0,00453
|
0,00295
|
18,357
|
| 08.sig
|
0
|
4,28
|
2,6
|
4,28
|
2,24468
|
747,61
|
0,00674
|
0,003023
|
12,729
|
Таблица 2.2. Численные значения спектральных параметров для Т80.
| Объeкты и файлы
|
FGmax1 Гц
|
FGmax2 Гц
|
FI0,5 Гц
|
FII0,5 Гц
|
m1f
|
m2f
|
Y
|
Kvf
|
Ef
|
| T80
|
00.sig
|
0
|
26,8
|
2,4
|
8,56
|
7,69704
|
2705,7
|
0,0219
|
0,002908
|
21,282
|
| 01.sig
|
0
|
3,65
|
2,7
|
2,17
|
8,12505
|
3029,1
|
0,02179
|
0,002742
|
31,832
|
| 02.sig
|
0
|
32,1
|
2,9
|
2,11
|
3,43561
|
946,36
|
0,01247
|
0,003676
|
10,364
|
| 03.sig
|
0
|
4,61
|
2,14
|
2,8
|
3,10695
|
1019,6
|
0,00947
|
0,003076
|
14,97
|
| 04.sig
|
0
|
53,5
|
2,14
|
8,56
|
8,77833
|
2627,5
|
0,02933
|
0,003442
|
14,236
|
| 05.sig
|
0
|
22,9
|
2,1
|
4,28
|
4,36341
|
1642,4
|
0,01159
|
0,002688
|
16,853
|
| 06.sig
|
0
|
3,21
|
2,55
|
8,56
|
4,01203
|
1240,2
|
0,01298
|
0,003278
|
7,0383
|
| 07.sig
|
0
|
2,19
|
2,6
|
4,28
|
3,73718
|
1187,4
|
0,01176
|
0,003185
|
6,4982
|
| 08.sig
|
0
|
2,67
|
2,11
|
4,3
|
4,88861
|
1851,8
|
0,01291
|
0,002674
|
14,526
|
Таблица 2.3. Численные значения спектральных параметров для СВК «Нона».
| Объeкты и файлы
|
FGmax1 Гц
|
Fgmax2 Гц
|
FI
0,5 Гц
|
FII
0,5 Гц
|
m1
f
|
m2
f
|
Y
|
Kvf
|
Ef
|
| Н О Н А
|
00.sig
|
0
|
3,21
|
2,45
|
6,42
|
0,15868
|
37,569
|
0,00067
|
0,004227
|
2,2374
|
| 01.sig
|
0
|
8,56
|
2,4
|
2,14
|
1,88624
|
675,27
|
0,00527
|
0,002808
|
22,301
|
| 02.sig
|
0
|
17,12
|
2,11
|
6,45
|
2,59006
|
707,99
|
0,00948
|
0,003693
|
3,3336
|
| 03.sig
|
0
|
153,01
|
2,8
|
4,28
|
1,92834
|
612,5
|
0,00607
|
0,003168
|
8,2517
|
Таблица 2.4. Численные значения спектральных параметров для РЛС "Пантера"
| Объeкты и файлы
|
FGmax1 Гц
|
FGmax2 Гц
|
FI
0,5 Гц
|
FII
0,5 Гц
|
m1
f
|
m2
f
|
Y
|
Kvf
|
Ef
|
| Пантера
|
00.sig
|
0
|
3,21
|
2,4
|
2,5
|
1,42944
|
459,86
|
0,00444
|
0,003122
|
4,5871
|
| 01.sig
|
0
|
110
|
2,7
|
6,42
|
2,11868
|
751,46
|
0,00597
|
0,002836
|
7,9046
|
| 02.sig
|
0
|
3,21
|
2,65
|
6,7
|
1,99105
|
738,57
|
0,00537
|
0,00271
|
7,5118
|
| 03.sig
|
0
|
4,28
|
2,8
|
8,56
|
2,27897
|
811,28
|
0,0064
|
0,002827
|
8,2188
|
Результаты анализа спектра квадратурной компоненты
Таблица 2.5. Спектр квадратурной компоненты для Т–80
| FGmax1 Гц
|
m1f
|
m2f
|
Y
|
Kvf
|
Энергия
|
Файл
|
Матожид
|
Медиана
|
СКО
|
СКО/МО
|
Шир 0,1 в Гц
|
| 331,7
|
5,307985
|
110,6747
|
0,254572
|
0,064339
|
2,64272
|
00.sig
|
0,276951
|
0,171306
|
0,256895
|
1,499628
|
38,52
|
| 349,89
|
2,832427
|
56,98559
|
0,140784
|
0,057848
|
13,50523
|
01.sig
|
0,163087
|
0,091314
|
0,186653
|
2,044088
|
38,52
|
| 39,59
|
3,246084
|
71,86384
|
0,146625
|
0,052931
|
11,38086
|
02.sig
|
0,185923
|
0,160384
|
0,13449
|
0,838546
|
33,17
|
| 172,27
|
0,954858
|
8,782213
|
0,103818
|
0,121322
|
0,775486
|
03.sig
|
0,140063
|
0,041501
|
0,198949
|
4,793802
|
25,68
|
| 28,89
|
6,192352
|
164,901
|
0,232535
|
0,04893
|
1,623435
|
04.sig
|
0,259159
|
0,21171
|
0,223028
|
1,05346
|
42,8
|
| 297,46
|
2,095472
|
26,63269
|
0,164873
|
0,094214
|
1,138936
|
05.sig
|
0,203181
|
0,079344
|
0,299011
|
3,768545
|
28,89
|
| 171,2
|
5,403319
|
81,75655
|
0,357107
|
0,102802
|
2,369707
|
06.sig
|
0,447377
|
0,418874
|
0,230918
|
0,551283
|
22,47
|
| 167,99
|
4,37673
|
92,0279
|
0,208152
|
0,06006
|
2,290224
|
07.sig
|
0,231934
|
0,120696
|
0,255052
|
2,113175
|
40,66
|
| 297,46
|
1,315523
|
13,54695
|
0,127748
|
0,111331
|
4,458267
|
08.sig
|
0,185779
|
0,052621
|
0,265928
|
5,053633
|
25,68
|
| 189,39
|
1,439827
|
138,9613
|
0,014919
|
0,010518
|
1,269775
|
09.sig
|
0,048613
|
0,015031
|
0,130835
|
8,704123
|
196,88
|
Таблица 2.6. Спектр квадратурной компоненты для ЗИЛ–131
| FGmax1 Гц
|
m1f
|
m2f
|
Y
|
Kvf
|
Энергия
|
Файл
|
Матожид
|
Медиана
|
СКО
|
СКО/МО
|
Шир 0,1 в Гц
|
| 633,44
|
9,590914
|
270,7091
|
0,339795
|
0,053663
|
1,034378
|
00.sig
|
0,371449
|
0,309108
|
0,285509
|
0,923654
|
42,8
|
| 374,5
|
5,590852
|
73,39129
|
0,425904
|
0,132693
|
4,30962
|
01.sig
|
0,512172
|
0,432797
|
0,261845
|
0,605006
|
21,4
|
| 492,2
|
9,188762
|
237,3151
|
0,355786
|
0,060104
|
9,706813
|
02.sig
|
0,410053
|
0,439397
|
0,202154
|
0,460071
|
42,8
|
| 401,25
|
3,813184
|
639,9777
|
0,02272
|
0,006097
|
4,655072
|
03.sig
|
0,071089
|
0,016061
|
0,155955
|
9,710459
|
423,72
|
| 471,87
|
1,428387
|
15,49555
|
0,131669
|
0,106158
|
1,621322
|
04.sig
|
0,190424
|
0,100218
|
0,224934
|
2,244448
|
27,82
|
| 488,99
|
5,295417
|
99,27395
|
0,282465
|
0,07434
|
3,023025
|
05.sig
|
0,348302
|
0,314815
|
0,178402
|
0,566687
|
28,89
|
| 383,06
|
8,450339
|
231,2949
|
0,308732
|
0,052852
|
2,763133
|
06.sig
|
0,343219
|
0,342934
|
0,201993
|
0,589016
|
42,8
|
| 439,77
|
5,463615
|
102,1836
|
0,292132
|
0,075535
|
6,183213
|
07.sig
|
0,340607
|
0,295082
|
0,247055
|
0,837243
|
28,89
|
| 343,47
|
6,166675
|
580,6637
|
0,06549
|
0,011364
|
2,951703
|
08.sig
|
0,114548
|
0,012574
|
0,193144
|
15,36013
|
365,94
|
Таблица 2.7. Спектр квадратурной компоненты для Т72
| FGmax
1 Гц
|
m
1
f
|
m
2
f
|
Y
|
Kvf
|
Энергия
|
Файл
|
Матожид
|
Медиана
|
СКО
|
СКО/МО
|
Шир 0,2 в Гц
|
| 331,7
|
4,699953
|
81,83516
|
0,269927
|
0,078666
|
2,64272
|
00.sig
|
0,306603
|
0,226265
|
0,256597
|
1,134058
|
34,24
|
| 349,89
|
1,524904
|
17,39855
|
0,133651
|
0,101166
|
13,50523
|
01.sig
|
0,198317
|
0,122216
|
0,216966
|
1,775266
|
25,68
|
| 39,59
|
3,33875
|
82,43641
|
0,135222
|
0,046834
|
11,38086
|
02.sig
|
0,172157
|
0,15254
|
0,128672
|
0,843528
|
40,66
|
| 172,27
|
0,954858
|
8,782213
|
0,103818
|
0,121322
|
0,775486
|
03.sig
|
0,140063
|
0,041501
|
0,198949
|
4,793802
|
25,68
|
| 28,89
|
6,192352
|
164,901
|
0,232535
|
0,04893
|
1,623435
|
04.sig
|
0,259159
|
0,21171
|
0,223028
|
1,05346
|
42,8
|
| 297,46
|
1,345564
|
13,20741
|
0,137085
|
0,118064
|
1,138936
|
05.sig
|
0,223581
|
0,079271
|
0,325783
|
4,10973
|
23,54
|
| 171,2
|
6,349417
|
110,0203
|
0,366433
|
0,09109
|
2,369707
|
06.sig
|
0,462445
|
0,439705
|
0,238512
|
0,542436
|
27,82
|
| 167,99
|
2,445437
|
29,3003
|
0,204099
|
0,104864
|
2,290224
|
07.sig
|
0,300887
|
0,149454
|
0,279338
|
1,869058
|
27,82
|
| 297,46
|
1,023153
|
9,868423
|
0,10608
|
0,115983
|
4,458267
|
08.sig
|
0,193933
|
0,052621
|
0,275348
|
5,232643
|
23,54
|
| 189,39
|
1,826612
|
16,6036
|
0,200951
|
0,13768
|
1,269775
|
09.sig
|
0,269271
|
0,154467
|
0,273096
|
1,767985
|
23,54
|
Таблица 2.8. Спектр квадратурной компоненты для РЛС "Пантера"
| FGmax
1 Гц
|
m
1
f
|
m
2
f
|
Y
|
Kvf
|
Энергия
|
Файл
|
Матожид
|
Медиана
|
СКО
|
СКО/МО
|
Шир 0,2 в Гц
|
| 333,44
|
9,657718
|
283,5316
|
0,328963
|
0,050761
|
1,662853
|
00.sig
|
0,356047
|
0,282348
|
0,29966
|
1,061313
|
42,8
|
| 374,5
|
1,816357
|
181,2959
|
0,018198
|
0,010204
|
4,30962
|
01.sig
|
0,061235
|
0,013494
|
0,160183
|
11,87045
|
25,38
|
| 492,2
|
9,188762
|
237,3151
|
0,355786
|
0,060104
|
9,706813
|
02.sig
|
0,410053
|
0,439397
|
0,202154
|
0,460071
|
42,8
|
| 401,25
|
3,752688
|
634,0224
|
0,022212
|
0,006053
|
4,655072
|
03.sig
|
0,069973
|
0,016049
|
0,154559
|
9,630375
|
422,65
|
| 471,87
|
0,88155
|
8,17328
|
0,095082
|
0,11919
|
1,621322
|
04.sig
|
0,176206
|
0,079189
|
0,235055
|
2,968273
|
23,54
|
| 488,99
|
5,357566
|
102,764
|
0,279315
|
0,07234
|
3,023025
|
05.sig
|
0,344956
|
0,313587
|
0,176191
|
0,561855
|
29,96
|
| 383,06
|
8,450339
|
231,2949
|
0,308732
|
0,052852
|
2,763133
|
06.sig
|
0,343219
|
0,342934
|
0,201993
|
0,589016
|
42,8
|
| 439,77
|
5,404812
|
99,25311
|
0,294318
|
0,077166
|
6,183213
|
07.sig
|
0,340202
|
0,289399
|
0,247139
|
0,853975
|
28,89
|
| 343,47
|
6,09408
|
115,0653
|
0,322754
|
0,078202
|
2,951703
|
08.sig
|
0,400016
|
0,319701
|
0,190735
|
0,596604
|
26,75
|
Анализ таблиц доплеровских спектров анализируемых целей показывает, что имеются существенные отличия в некоторых спектральных признаках для классов гусеничных и колёсных целей. Указанные отличия могут быть использованы при синтезе классификатора МНЦ по спектральным моментам.
Анализ поляризационных признаков классификации
Таблица 2.9. Поляризационные характеристики Зил 131
| Автомобиль Зил–131 бортовой, неподвижный, не работающий двигатель
|
| Ракурс цели
|
Лоб
|
Лоб 45є
|
Борт
|
Корма 45є
|
Корма
|
| Стат. оценки
|
МО
|
| Поляризационные признаки
|
L1
|
0,094232
|
0,433034
|
0,275402
|
0,342681
|
0,31486
|
| L
|
–13,3708
|
–14,8733
|
–17,0783
|
–14,45
|
–19,5688
|
| Z
|
3,160245
|
–4,84648
|
5,599695
|
4,604861
|
5,475064
|
| q
|
0,36075
|
0,488521
|
0,567157
|
0,476581
|
0,539105
|
|
|
0,336754
|
–0,4871
|
0,565439
|
0,465756
|
0,537527
|
|
|
34,25688
|
30,069
|
27,67729
|
30,4512
|
28,33317
|
|
|
4,405942
|
0,328807
|
0,175407
|
2,738056
|
0,312402
|
| m
|
0,78139
|
0,099526
|
0,142886
|
0,627589
|
0,147331
|
|
|
1,206262
|
0,76164
|
1,381557
|
1,312969
|
1,380128
|
|
|
1,206262
|
0,76164
|
1,381557
|
1,312969
|
1,380128
|
| R
|
0,000909
|
0,026238
|
0,010182
|
0,015803
|
0,012305
|
| Q0
|
0,002566
|
0,046311
|
0,015623
|
0,027958
|
0,022926
|
| СКО
|
| L1
|
0,019933
|
0,08968
|
0,022291
|
0,060829
|
0,030241
|
| L
|
2,193937
|
3,827161
|
0,96052
|
1,945445
|
1,707972
|
| Z
|
1,085685
|
1,261026
|
0,37084
|
1,373203
|
0,590785
|
| q
|
0,095926
|
0,100579
|
0,02877
|
0,11518
|
0,0452
|
|
|
0,109852
|
0,100525
|
0,028779
|
0,118769
|
0,045089
|
|
|
2,966826
|
3,430928
|
1,004118
|
3,817299
|
1,578053
|
|
|
3,977784
|
0,464922
|
0,094412
|
2,957522
|
0,192331
|
| m
|
0,470903
|
0,094526
|
0,060233
|
0,337639
|
0,076588
|
|
|
0,07314
|
0,053537
|
0,029561
|
0,104024
|
0,047677
|
|
|
0,07314
|
0,053537
|
0,029561
|
0,104024
|
0,047677
|
| R
|
0,000513
|
0,013363
|
0,001841
|
0,007755
|
0,002895
|
| Q0
|
0,000895
|
0,018993
|
0,002487
|
0,008326
|
0,004259
|
Таблица 2.10. Поляризационные характеристики МТЛБУ «Пантера»
| МТЛБУ Пантера, неподвижный, не работающий двигатель
|
| Ракурс цели
|
Лоб
|
Лоб 45є
|
Борт
|
Корма 45є
|
Корма
|
| Стат. оценки
|
МО
|
| Поляризационные признаки
|
L1
|
0,166416
|
0,492208
|
0,712044
|
0,337278
|
1,793774
|
| L
|
–22,3677
|
–26,8106
|
–11,8818
|
–2,83019
|
–12,0602
|
| Z
|
1,888799
|
18,72558
|
4,142757
|
0,581457
|
0,355925
|
| q
|
0,226764
|
0,968583
|
0,451085
|
0,377313
|
0,210481
|
|
|
0,210401
|
0,966866
|
0,433502
|
0,061063
|
0,03969
|
|
|
38,4029
|
6,817603
|
31,41444
|
33,3854
|
38,89569
|
|
|
1,34555
|
0,171819
|
3,31677
|
27,28023
|
2,847303
|
| m
|
0,074316
|
0,154774
|
1,68131
|
9,651769
|
0,336332
|
|
|
1,117889
|
2,989174
|
1,274022
|
1,042305
|
1,027606
|
|
|
1,117889
|
2,989174
|
1,274022
|
1,060414
|
1,027606
|
| R
|
0,001254
|
0,061778
|
0,057818
|
0,017404
|
0,119522
|
| Q0
|
0,009232
|
0,032998
|
0,127231
|
0,03979
|
1,111855
|
| СКО
|
| L1
|
0,010734
|
0,047099
|
0,111916
|
0,168314
|
0,147582
|
| L
|
2,65691
|
4,745816
|
0,931295
|
1,312864
|
1,751585
|
| Z
|
0,512133
|
2,556228
|
1,129651
|
1,703014
|
1,050355
|
| q
|
0,04596
|
0,016895
|
0,103685
|
0,19733
|
0,082049
|
|
|
0,056041
|
0,01731
|
0,101186
|
0,178063
|
0,117007
|
|
|
1,357457
|
1,91249
|
3,391287
|
6,512995
|
2,401711
|
|
|
2,027432
|
0,136221
|
1,629226
|
9,727616
|
4,922703
|
| m
|
0,047189
|
0,121146
|
0,625049
|
6,704142
|
0,279627
|
|
|
0,032187
|
0,461026
|
0,084058
|
0,119843
|
0,06096
|
|
|
0,032187
|
0,461026
|
0,084058
|
0,108099
|
0,06096
|
| R
|
0,000364
|
0,011736
|
0,031293
|
0,02049
|
0,070178
|
| Q0
|
0,001141
|
0,006303
|
0,031058
|
0,03479
|
0,165263
|
Таблица 2.11. Поляризационные характеристики танка Т–72
| Танк Т–72, неподвижный, не работающий двигатель
|
| Стат. оценки
|
МО
|
| Поляризационные признаки
|
L1
|
0,224896
|
0,30789
|
0,185067
|
0,208336
|
0,462812
|
| L
|
–11,2572
|
–4,35086
|
–6,41593
|
–13,2299
|
–3,34028
|
| Z
|
8,407537
|
4,373034
|
8,001983
|
13,87233
|
–4,77292
|
| q
|
0,746225
|
0,581362
|
0,721452
|
0,892992
|
0,495071
|
|
|
0,735278
|
0,460568
|
0,70498
|
0,886434
|
–0,45849
|
|
|
20,59323
|
27,1034
|
21,40566
|
12,2694
|
29,51101
|
|
|
0,662972
|
13,85547
|
1,914046
|
0,502713
|
5,038862
|
| m
|
0,880306
|
7,506303
|
0,732187
|
0,497886
|
1,852777
|
|
|
1,630668
|
1,288219
|
1,598075
|
2,299289
|
0,772037
|
|
|
1,630668
|
1,288219
|
1,598075
|
2,299289
|
0,772037
|
| R
|
0,009958
|
0,013743
|
0,00629
|
0,010556
|
0,037113
|
| Q0
|
0,008497
|
0,020077
|
0,006163
|
0,006282
|
0,050184
|
| СКО
|
| L1
|
0,030064
|
0,045618
|
0,02792
|
0,03756
|
0,143958
|
| L
|
1,351466
|
1,903667
|
0,812072
|
2,01048
|
1,528524
|
| Z
|
1,454214
|
0,650255
|
1,490407
|
2,376265
|
2,150214
|
| q
|
0,073828
|
0,076108
|
0,082861
|
0,053821
|
0,1673
|
|
|
0,074036
|
0,061461
|
0,081411
|
0,05529
|
0,18282
|
|
|
3,191392
|
2,584006
|
3,484787
|
3,170432
|
5,654013
|
|
|
0,400243
|
6,603283
|
0,807243
|
0,347423
|
5,475376
|
| m
|
0,288309
|
3,663191
|
0,35539
|
0,26036
|
0,763436
|
|
|
0,138599
|
0,046776
|
0,139293
|
0,327507
|
0,096274
|
|
|
0,138599
|
0,046776
|
0,139293
|
0,327507
|
0,096274
|
| R
|
0,003393
|
0,004652
|
0,001926
|
0,003914
|
0,030276
|
| Q0
|
0,001822
|
0,006513
|
0,001908
|
0,002044
|
0,024186
|
Таблица 2.12. Поляризационные характеристики танка Т–80
| Танк Т–80, неподвижный, не работающий двигатель
|
| Ракурс цели
|
Лоб
|
Лоб 45є
|
Борт
|
Корма 45є
|
Корма
|
| Стат. оценки
|
МО
|
| Поляризационные признаки
|
L1
|
0,209698
|
0,488495
|
0,171005
|
0,065102
|
0,17339
|
| L
|
–5,45199
|
–10,5038
|
–3,29514
|
–5,46188
|
–15,3732
|
| Z
|
1,03339
|
7,533988
|
6,036348
|
2,027092
|
5,858997
|
| q
|
0,357116
|
0,673347
|
0,649309
|
0,27296
|
0,587636
|
|
|
0,102929
|
0,622793
|
0,591315
|
0,218506
|
0,585106
|
|
|
34,14424
|
22,61325
|
24,55047
|
36,9069
|
26,95605
|
|
|
15,13244
|
3,544402
|
5,988099
|
10,61168
|
0,335245
|
| m
|
2,709222
|
1,152643
|
3,504685
|
1,741393
|
0,176835
|
|
|
1,084693
|
1,59243
|
1,420184
|
1,13129
|
1,402433
|
|
|
1,084693
|
1,59243
|
1,420184
|
1,13129
|
1,402433
|
| R
|
0,005342
|
0,058432
|
0,005168
|
0,000313
|
0,004272
|
| Q0
|
0,015485
|
0,051026
|
0,005753
|
0,001365
|
0,006153
|
| СКО
|
| L1
|
0,074156
|
0,155853
|
0,036947
|
0,013433
|
0,017009
|
| L
|
1,842625
|
3,183862
|
0,727899
|
3,840953
|
1,652025
|
| Z
|
1,829048
|
3,080193
|
0,902082
|
1,55681
|
0,543002
|
| q
|
0,159435
|
0,159702
|
0,064887
|
0,138377
|
0,040344
|
|
|
0,18149
|
0,181096
|
0,067142
|
0,163082
|
0,040728
|
|
|
5,088879
|
6,421146
|
2,43493
|
4,247888
|
1,432779
|
|
|
9,210268
|
3,453614
|
3,897232
|
7,735721
|
0,231504
|
| m
|
1,790785
|
1,112722
|
2,199243
|
1,100824
|
0,110846
|
|
|
0,115574
|
0,293637
|
0,073579
|
0,101694
|
0,043955
|
|
|
0,115574
|
0,293637
|
0,073579
|
0,101694
|
0,043955
|
| R
|
0,004812
|
0,036243
|
0,002394
|
0,000297
|
0,000943
|
| Q0
|
0,010442
|
0,030202
|
0,00229
|
0,000438
|
0,001211
|
2.3 Анализ поляризационных признаков классификация использованных целей
Рассчитанные поляризационные параметры подвергались статистической обработке в соответствии с методикой обработки экспериментальных данных, рассмотренной в [1-3].
Некоторые численные значения поляризационных признаков приведены в таблицах 2.9.-2.12, полностью поляризационные признаки приведены в приложении 2, а гистограммы поляризационных параметров в качестве иллюстрации показаны на рис. 2.18 – 2.27.
Анализ полученных результатов позволяет сформулировать следующие предположения:
1. Энергетический параметр moL
1
( полная ЭПР объекта) может быть использован как самостоятельно, так и в составе группы признаков для решения задачи обнаружения МНЦ на фоне подстилающей поверхности.
2. Значения ЭПР отраженных сигналов от МНЦ при согласованных поляризациях в–в и г–г представляют собой величины приблизительно равного порядка. Это обуславливает близость значений рассчитанных параметров Z для исследуемых объектов. При этом ЭПР подстилающей поверхности отличается от ЭПР МНЦ, что вызывает отличие параметров Z для фона от соответствующих параметров МНЦ. Однако привлечение этих параметров для селекции МНЦ затруднено широкими пределами их изменения для подстилающей поверхности.
3. СКО коэффициентов деполяризации L и Z имеют достаточно низкую дивергенцию при вариации объектов локации (от 2 до 8 дб), в то же время численные значения этих параметров для подстилающей поверхности отличаются в 5–6 раз, что указывает на принципиальную возможность использования коэффициентов деполяризации для обнаружения объектов.
Гистограммы распределения поляризационных признаков некоторых радиолокационных объектов и подстилающей поверхности
  Рис.2.18. Гистограмма распределения признака L1 автомобиля Зил–131, ракурс – борт
  Рис.2.19. Гистограмма распределения признака L1 танка Т–72, ракурс – борт
  Рис.2.20. Гистограмма распределения признака L1 танка Т–80, ракурс – борт
  Рис.2.21. Гистограмма распределения признака L1 подстилающей поверхности
  Рис.2.22. Гистограмма распределения признака L1 кустарника
  Рис.2.23. Гистограмма распределения признака L1 опоры ЛЭП
  Рис.2.24. Гистограмма распределения признака m автомобиля Зил–131, ракурс – борт

Рис.2.25. Гистограмма распределения признака m танка Т–72, ракурс – борт
 
Рис.2.26. Гистограмма распределения признака m танка Т–80, ракурс – борт  
Рис.2.27. Гистограмма распределения признака m подстилающей поверхности полностью перекрываются подстилающей поверхностью.
Однако признаки skoτm
и skoψm
имеют отличия от 5 до 10 раз между объектами класса «подстилающая поверхность» и МНЦ, что целесообразно использовать для их обнаружения на фоне изотропной по поляризации подстилающей поверхности.
4. Вопреки ожиданиям инвариант цели μ и статистически связанный с ним параметр q(их mo) не обладают большой разделимостью и не могут быть использованы для решения задач обнаружения и классификации. Однако и skoμ и skoq для МНЦ и подстилающей поверхности отличаются в некоторых случаях более, чем на порядок.
5. Мерой способности цели поляризовать подающее неполяризованное излучение является дескриптор G1 (gam). Анализ приложения 1 показывает, что использовать G1 в качестве одиночного самостоятельного признака для обнаружения (распознавания) МНЦ нецелесообразно. Применение G1 в составе комплексного параметра Qo
может быть использовано при обнаружении МНЦ на фоне подстилающей поверхности, если вместо G1 в соотношение для Qo
подставить σG
1
, который для МНЦ и подстилающей поверхности отличается в 5 и более раз. Таким образом, проведение записей реализаций сигналов, отраженных от объектов техники, объектов антропогенного и неантропогенного происхождения с применением 14–разрядного АЦП позволило исследовать статистические характеристики целей и подстилающей поверхности, что является исходным материалом для составления априорного словаря признаков селекции МНЦ на фоне
2.4 Анализ корреляционных связей поляризационных характеристик и оценка их эффективности
Известно [24,25], что взаимная коррелированность компонент отраженного сигнала снижает информативность выделяемых на их основе признаков селекции-распознавания, поэтому целесообразно оценить степень коррелированности исследуемых ПХ. Для решения этой задачи по методике, достаточно подробно рассмотренной в работах автора, производилась оценка полной корреляционной матрицы поляризационных параметров сигналов, отраженных от целей и подстилающей поверхности.
Уместно отметить, что численные значения 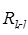 коэффициентов корреляции между параметрами Хк
и Хс
, составляющих корреляционную матрицу, близки к значениям, полученным в [1–5], при сохранении тех же общих тенденций. Анализ полученной базы данных показал, что значения коэффициентов корреляции ПХ колеблются от 0 до 0,9. Для подстилающей поверхности в целом характерен пониженный уровень коррелированности ПХ. коэффициентов корреляции между параметрами Хк
и Хс
, составляющих корреляционную матрицу, близки к значениям, полученным в [1–5], при сохранении тех же общих тенденций. Анализ полученной базы данных показал, что значения коэффициентов корреляции ПХ колеблются от 0 до 0,9. Для подстилающей поверхности в целом характерен пониженный уровень коррелированности ПХ.
В качестве примера в таблицах 2.13 – 2.15 приведены корреляционные матрицы поляризационных параметров подстилающей поверхности и целей.
Полностью корреляционные матрицы поляризационных параметров приведены в приложении 3
Таблица 2.13. Коэффициенты взаимной корреляции поляризационных признаков
| автомобиля Зил–131, ракурс – борт
|
| L1
|
L
|
Z
|
q
|
|
|
|
m
|
1
|
R
|
Q0
|
| L1
|
1
|
0,1452
|
–0,03
|
–0,03
|
–0,032
|
0,0288
|
0,1006
|
0,2272
|
–0,146
|
0,7962
|
0,923974
|
| L
|
0,1452
|
1
|
–0,438
|
–0,422
|
–0,435
|
0,4232
|
–0,439
|
0,7796
|
–0,939
|
–0,132
|
0,290707
|
| Z
|
–0,03
|
–0,438
|
1
|
0,9992
|
0,9994
|
–1
|
0,4611
|
–0,158
|
0,1128
|
0,5769
|
–0,40571
|
| q
|
–0,03
|
–0,422
|
0,9992
|
1
|
0,9999
|
–1
|
0,4586
|
–0,144
|
0,0945
|
0,5775
|
–0,4067
|
|
|
–0,032
|
–0,435
|
0,9994
|
0,9999
|
1
|
–1
|
0,4628
|
–0,156
|
0,1095
|
0,5756
|
–0,40854
|
|
|
0,0288
|
0,4232
|
–1
|
–1
|
–1
|
1
|
–0,458
|
0,1448
|
–0,096
|
–0,578
|
0,405352
|
|
|
0,1006
|
–0,439
|
0,4611
|
0,4586
|
0,4628
|
–0,458
|
1
|
0,1323
|
0,3194
|
0,3544
|
–0,08364
|
| m
|
0,2272
|
0,7796
|
–0,158
|
–0,144
|
–0,156
|
0,1448
|
0,1323
|
1
|
–0,812
|
0,0979
|
0,26265
|
| 1
|
–0,146
|
–0,939
|
0,1128
|
0,0945
|
0,1095
|
–0,096
|
0,3194
|
–0,812
|
1
|
–0,066
|
–0,16784
|
| R
|
0,7962
|
–0,132
|
0,5769
|
0,5775
|
0,5756
|
–0,578
|
0,3544
|
0,0979
|
–0,066
|
1
|
0,506167
|
| Q0
|
0,924
|
0,2907
|
–0,406
|
–0,407
|
–0,409
|
0,4054
|
–0,084
|
0,2627
|
–0,168
|
0,5062
|
1
|
Таблица 2.14. Коэффициенты взаимной корреляции поляризационных признаков
| Пантеры МТЛБУ, ракурс – борт
|
| L1
|
L
|
Z
|
q
|
|
|
|
m
|
1
|
R
|
Q0
|
| L1
|
1
|
–0,808
|
0,5879
|
0,5449
|
0,5754
|
–0,552
|
0,0024
|
0,7617
|
0,1397
|
0,8651
|
0,876333
|
| L
|
–0,808
|
1
|
–0,491
|
–0,415
|
–0,459
|
0,4328
|
0,038
|
–0,921
|
–0,411
|
–0,718
|
–0,71674
|
| Z
|
0,5879
|
–0,491
|
1
|
0,9923
|
0,996
|
–0,997
|
–0,271
|
0,383
|
–0,59
|
0,8726
|
0,133339
|
| q
|
0,5449
|
–0,415
|
0,9923
|
1
|
0,9987
|
–0,999
|
–0,258
|
0,3042
|
–0,651
|
0,8331
|
0,080503
|
|
|
0,5754
|
–0,459
|
0,996
|
0,9987
|
1
|
–0,999
|
–0,259
|
0,3482
|
–0,613
|
0,8533
|
0,116524
|
|
|
–0,552
|
0,4328
|
–0,997
|
–0,999
|
–0,999
|
1
|
0,2644
|
–0,324
|
0,6397
|
–0,845
|
–0,08941
|
|
|
0,0024
|
0,038
|
–0,271
|
–0,258
|
–0,259
|
0,2644
|
1
|
–0,029
|
0,2223
|
–0,2
|
0,166778
|
| m
|
0,7617
|
–0,921
|
0,383
|
0,3042
|
0,3482
|
–0,324
|
–0,029
|
1
|
0,4556
|
0,6444
|
0,720748
|
| 1
|
0,1397
|
–0,411
|
–0,59
|
–0,651
|
–0,613
|
0,6397
|
0,2223
|
0,4556
|
1
|
–0,24
|
0,526638
|
| R
|
0,8651
|
–0,718
|
0,8726
|
0,8331
|
0,8533
|
–0,845
|
–0,2
|
0,6444
|
–0,24
|
1
|
0,545609
|
| Q0
|
0,8763
|
–0,717
|
0,1333
|
0,0805
|
0,1165
|
–0,089
|
0,1668
|
0,7207
|
0,5266
|
0,5456
|
1
|
Таблица 2.15. Коэффициенты взаимной корреляции поляризационных признаков
| танка Т–72, ракурс – борт
|
| L1
|
L
|
Z
|
q
|
|
|
|
m
|
1
|
R
|
Q0
|
| L1
|
1
|
–0,814
|
0,4444
|
0,4667
|
0,483
|
–0,447
|
–0,188
|
–0,567
|
0,0261
|
0,9298
|
0,929347
|
| L
|
–0,814
|
1
|
–0,395
|
–0,401
|
–0,424
|
0,3859
|
0,2343
|
0,5585
|
–0,17
|
–0,746
|
–0,76508
|
| Z
|
0,4444
|
–0,395
|
1
|
0,9813
|
0,9819
|
–0,995
|
–0,179
|
–0,301
|
–0,828
|
0,643
|
0,102402
|
| q
|
0,4667
|
–0,401
|
0,9813
|
1
|
0,9995
|
–0,995
|
–0,201
|
–0,315
|
–0,786
|
0,6366
|
0,126916
|
|
|
0,483
|
–0,424
|
0,9819
|
0,9995
|
1
|
–0,995
|
–0,193
|
–0,326
|
–0,774
|
0,6497
|
0,145336
|
|
|
–0,447
|
0,3859
|
–0,995
|
–0,995
|
–0,995
|
1
|
0,1914
|
0,3013
|
0,8197
|
–0,635
|
–0,10303
|
|
|
–0,188
|
0,2343
|
–0,179
|
–0,201
|
–0,193
|
0,1914
|
1
|
0,0169
|
0,0506
|
–0,179
|
–0,14026
|
| m
|
–0,567
|
0,5585
|
–0,301
|
–0,315
|
–0,326
|
0,3013
|
0,0169
|
1
|
–0,018
|
–0,499
|
–0,49201
|
| 1
|
0,0261
|
–0,17
|
–0,828
|
–0,786
|
–0,774
|
0,8197
|
0,0506
|
–0,018
|
1
|
–0,223
|
0,353196
|
| R
|
0,9298
|
–0,746
|
0,643
|
0,6366
|
0,6497
|
–0,635
|
–0,179
|
–0,499
|
–0,223
|
1
|
0,779709
|
| Q0
|
0,9293
|
–0,765
|
0,1024
|
0,1269
|
0,1453
|
–0,103
|
–0,14
|
–0,492
|
0,3532
|
0,7797
|
1
|
Их анализ позволяет сделать следующие выводы [1–5]:
1. Практически некоррелированным с остальными является параметр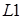 , (за исключением Q0
), который является мерой размеров объекта. , (за исключением Q0
), который является мерой размеров объекта.
2. Высокую степень корреляции имеют комплексные параметры и параметры, от которых они зависят: Q0
от L1, K1
от τ
, K2
от τ
, K2
от  ψ
и т.д. Очевидно, что совместное их использование для обнаружения/классификации нецелесообразно.
ψ
и т.д. Очевидно, что совместное их использование для обнаружения/классификации нецелесообразно.
3. Физически обусловлено наличие сильной корреляции между дескриптором G1 коэффициентами деполяризации L, Z и коэффициентами анизотропии g и μ, поскольку в формировании этих признаков во всех случаях основную роль играет соотношение основных и кроссовых компонентов.
4. Низкой степенью корреляции между собой и с другими ПХ обладают параметры 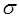 τ
, τ
,  ψ
, Q0
, L1, что является предпосылкой для их применения в группе для решения задачи классификации неподвижных МНЦ.
ψ
, Q0
, L1, что является предпосылкой для их применения в группе для решения задачи классификации неподвижных МНЦ.
5. Как показано в 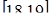 и последующих исследованиях применение коэффициентов взаимной корреляции между основными компонентами (основной и кроссовой) малоэффективно. Использование корреляции между отдельными ПХ также не может быть положено в основу синтеза алгоритмов обнаружения/классификации, поскольку такие параметры обладают высокой степенью изменчивости при вариации объектов внутри класса. и последующих исследованиях применение коэффициентов взаимной корреляции между основными компонентами (основной и кроссовой) малоэффективно. Использование корреляции между отдельными ПХ также не может быть положено в основу синтеза алгоритмов обнаружения/классификации, поскольку такие параметры обладают высокой степенью изменчивости при вариации объектов внутри класса.
В работах 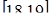 была достаточно подробно описана методика оценки эффективности признаков априорного словаря и выбор рабочего словаря. Не останавливаясь на отдельных ее положениях, отметим основные этапы. После составления априорного словаря необходимо решить ряд задач: была достаточно подробно описана методика оценки эффективности признаков априорного словаря и выбор рабочего словаря. Не останавливаясь на отдельных ее положениях, отметим основные этапы. После составления априорного словаря необходимо решить ряд задач:
1. На основе априорного словаря составить рабочий словарь, в который целесообразно включить только те признаки, которые незначительно коррелированны между собой и наиболее эффективны.
2. Описать классы объектов на языке признаков, то есть определить функции ПРВ признаков W(X1
, …, Xn
), где N – число признаков, при условии, что объекты принадлежат определенному классу.
3. Разработать алгоритмы селекции, обеспечивающие отнесение объектов к одному из двух классов: классу W1
– МНЦ и классу W2
– подстилающие поверхности. При этом алгоритмы селекции основываются на сравнении меры сходства селектируемых объектов с каждым классом.
4. Оценить эффективность разработанных алгоритмов селекции. При этом выбранный критерий качества должен быть максимальным. В качестве такого критерия могут быть использованы вероятность правильного решения задачи обнаружения МНЦ на фоне подстилающей поверхности, средний объем выборки из словаря признаков, необходимый для обнаружения МНЦ с заданной ошибкой и т.д. [13]. Оценка значений выбранной совокупности показателей эффективности системы проводится с помощью ее математической модели. При этом используются элементы обучения системы селекции, т.е. окончательный вариант рабочего словаря определяется максимумом эффективности системы.
Получить аналитические модели оценки вероятностей ошибок классификации удается далеко не всегда. Для оценки эффективности признаков классификации целесообразно использовать метод Монте-Карло. Для реализации этого метода на практике задаются вероятностью ошибки, полученной экспериментально, то есть, выбрав набор признаков, строят байесовский классификатор и экспериментально подсчитывают число ошибок классификации. Как показано в [18] эта процедура является гибкой, не зависит от вида распределений и позволяет найти оптимальное решение.
Известно [18], что байесовский классификатор обеспечивает отнесение объекта, заданного своим вектором признаков X к классу Wi
, если выполняется условие
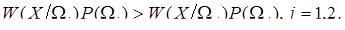 (2.18) (2.18)
На вход байесовского классификатора подаются значения признаков, рассчитанных на основе экспериментальных записей отраженных сигналов. На выходе синтезированного классификатора производится оценка вероятности получения правильных и обычных решений, в качестве которой служит отношение количества правильных ответов Ni*
к общему числу испытаний Ni
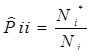 (2.19) (2.19)
Безусловная вероятность правильного обнаружения объекта системой селекции при предъявлении ей K–го признака из совокупности 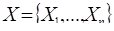 определятся как определятся как 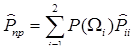 , а безусловная вероятность ошибочных решений , а безусловная вероятность ошибочных решений 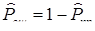 . .
Решение задач обнаружения неподвижной МНЦ (колесной или бронированной) на фоне отражений от подстилающей поверхности и классификации МНЦ (колесная/гусеничная) производилось раздельно. Подразумеваются, что классификация при необходимости производится после решения задач обнаружения. Усредненные значения безусловных вероятностей ошибочных решений при использовании признаков априорного словаря приведены в таблице 2.16.
Таблица 2.16. Усреднённые значения безусловных вероятностей при использовании признаков априорного словаря Усреднённые значения безусловных вероятностей при использовании признаков априорного словаря
| 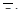
|
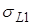
|
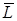
|
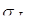
|
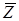
|
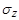
|
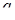
|
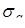
|
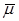
|
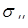
|

|
|
|
| Подстилающая.
поверхность
|
0,19
|
0,21
|
0,35
|
0,31
|
0,34
|
0,38
|
0,41
|
0,21
|
0,34
|
0,20
|
0,51
|
0,54
|
0,48
|
| МНЦ
|
0,21
|
0,19
|
0,34
|
0,33
|
0,33
|
0,41
|
0,37
|
0,19
|
0,35
|
0,18
|
0,49
|
0,51
|
0,44
|
| Искусств.объекты
|
0,31
|
0,32
|
0,49
|
0,54
|
0,43
|
0,51
|
0,41
|
0,24
|
0,37
|
0,21
|
0,47
|
0,49
|
0,47
|
Продолжение таблицы 2.16
|  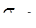
|
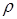
|
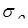
|
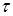
|
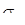
|
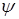
|
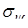
|
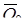
|
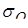
|
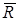
|
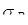
|
| 0,39
|
0,29
|
0,31
|
0,25
|
0,29
|
0,34
|
0,38
|
0,19
|
0,22
|
0,19
|
0,24
|
| 0,39
|
0,27
|
0,32
|
0,31
|
0,29
|
0,35
|
0,36
|
0,20
|
0,23
|
0,19
|
0,21
|
| 0,41
|
0,33
|
0,37
|
0,34
|
0,31
|
0,41
|
0,43
|
0,25
|
0,27
|
0,19
|
0,23
|
Анализ таблицы 2.16 позволяет сделать следующие выводы:
1. Наилучшими разделяющими свойствами классов МНЦ/подстилающая поверхность обладает группа комплексных параметров 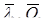 параметры, связанные с коэффициентами анизотропии параметры, связанные с коэффициентами анизотропии 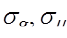 , параметры , параметры 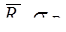 , параметры , параметры 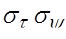
2. Указанные четыре группы параметров коррелированы внутри группы (например 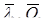 ), поэтому целесообразно использовать только один из них. ), поэтому целесообразно использовать только один из них.
3. В рабочий словарь признаков обнаружения целесообразно включить четыре параметра, например: 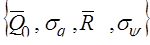 или любую возможную комбинацию из приведенных параметров, которые будут обладать приблизительно равной эффективностью. Аналогичные исследования были проведены для выявления признаков рабочего словаря при использовании классов гусеничная/колесная техника. Наименьшие ошибки классификации получены при использовании признаков или любую возможную комбинацию из приведенных параметров, которые будут обладать приблизительно равной эффективностью. Аналогичные исследования были проведены для выявления признаков рабочего словаря при использовании классов гусеничная/колесная техника. Наименьшие ошибки классификации получены при использовании признаков 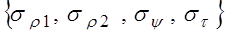 . Очевидно, что включение в рабочий словарь коррелированных признаков . Очевидно, что включение в рабочий словарь коррелированных признаков 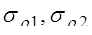 нецелесообразно, поскольку они обладают приблизительно равной эффективностью. Вариант рабочего словаря признаков классификации может иметь вид нецелесообразно, поскольку они обладают приблизительно равной эффективностью. Вариант рабочего словаря признаков классификации может иметь вид
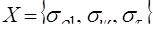 . .
3. Программное обеспечение
3.1 Комплекса программных средств (КПС) и его условное обозначение
Полное наименование КПС – программное обеспечение системы распознавания радиолокационных сигналов в мм диапазоне волн. Условное обозначение – СР РЛС.
Заказчиком КПС «Программное обеспечение системы распознавания радиолокационных сигналов в мм диапазоне волн» является ТулГУ, кафедра АИУС.
Назначение КПС –
распознавания радиолокационных сигналов в мм диапазоне волн.
Цели создания КПС –
Разработать программный комплекс (ПК) для селекции объектов, с помощью радиолокационных сигналов в мм диапазоне волн.
3.2 Характеристика объектов автоматизации
Объект автоматизации – процесс сортировки отраженных сигналов, для классификации объектов. Объектом является техника гусеничного или колесного типа.
Схема и алгоритм обработки данных, формат выходных данных представляет собой многоузловую иерархическую систему с элементами самообучения и графически представлена на рисунках 3.1, 3.2, 3.3

Рис. 3.1. Приемное устройство входных сигналов
Входные данные (детерминированный РЛС–сигнал) поступают с приемного устройства
на устройство обработки данных, всякая задача, для которой неизвестен алгоритм решения, априорно относится к искусственному интеллекту. В таких задачах программе предоставляется свобода выбора действия в условиях неопределенности. Именно эта свобода действия является существенной составляющей интеллекта, как естественного, так и искусственного, но такие алгоритмы сильно «утяжеляют» системы обработки информации, у нас же структура программных средств неизменна и представлена следующим алгоритмом:
| База данных составляется из эталонных сигналов, (совокупность характеристик объекта)
|
|
  Рис. 3.2. Алгоритм распознавания и обнаружения целей.
После обработки данных, на выходе получаем систему классификации цели с заданной вероятностью (порог вероятности распознавания определенного класса цели возможно варьировать и тем улучшать характеристики алгоритма в любом направлении – этим достигается требование интеллектуальности системы), для удобство восприятия пользователя (оператора) выходную информацию приводим к следующему виду – документов прилагаемой формы:

Рис. 3.3. Классификация объектов (выходные данные)
Сведения об условиях эксплуатации КПС: данный КПС будет эксплуатироваться в идеальных условиях. Для работы не требуется специализированных навыков. Необходимо наличие программного обеспечения и ЭВМ.
Состав к КПС в целом:
КПС состоит из программных модулей для ввода исходной информации, моделирования процесса распознавания (селекции), вывода полученной информации в виде графиков и таблиц.
Структура функционирования КПС: КПС стабильно функционирует, обеспечивает легкий доступ к информации, гибок и компактен, открыт для внесения изменений и дополнений.
Для удобства внесение изменений и улучшений приведен листинг программы:
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs,
StdCtrls, ExtCtrls, TeeProcs, TeEngine, Chart, Series, ComCtrls, TeeFunci;
type
TForm1 = class(TForm) {ОБЪЕКТЫ ОКНА}
Chart1: TChart;
Label1: TLabel;
Button1: TButton;
Button2: TButton;
ProgressBar1: TProgressBar;
Label2: TLabel;
CheckBox1: TCheckBox;
CheckBox2: TCheckBox;
CheckBox3: TCheckBox;
CheckBox4: TCheckBox;
Label3: TLabel;
Label4: TLabel;
Label5: TLabel;
Label6: TLabel;
Label7: TLabel;
Label9: TLabel;
Label10: TLabel;
CheckBox5: TCheckBox;
Label11: TLabel;
Series1: TPointSeries;
Series2: TPointSeries;
Series3: TPointSeries;
Series4: TPointSeries;
Series5: TPointSeries;
Series6: TPointSeries;
Series7: TPointSeries;
Series8: TPointSeries;
Series9: TPointSeries;
Series10: TPointSeries;
Series11: TPointSeries;
Series12: TPointSeries;
Series13: TPointSeries;
Series14: TPointSeries;
Series15: TPointSeries;
Series16: TPointSeries;
Series17: TPointSeries;
Series18: TPointSeries;
Series19: TPointSeries;
Series20: TPointSeries;
Series21: TPointSeries;
Series22: TPointSeries;
Series23: TPointSeries;
Series24: TPointSeries;
Series25: TPointSeries;
Button3: TButton;
Series26: TPointSeries;
Series27: TPointSeries;
Series28: TPointSeries;
Series29: TPointSeries;
Series30: TPointSeries;
Label8: TLabel;
procedure Button2Click(Sender: TObject);
procedure Button1Click(Sender: TObject);
procedure Button3Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
{Работа с Файлом Sign01.txt}
function DoFileDialog(Window: HWnd;
FilePath, DialogName, Caption: PChar): Boolean;
function DoFileOpen(Window: HWnd; FilePath: PChar): Boolean;
function DoFileSave(Window: HWnd; FilePath: PChar): Boolean;
var
Form1: TForm1;
ind:byte = 0;
implementation
type
TRec = Integer;
PSYV = ^TSYV;
TSYV = Longint;
THRec = THandle;
TCL = Integer;
TALC = Longint;
THKP = Word;
type
TDF = function(dirq: Integer; InP, OutP: Pointer; Max: Integer;
Context, Data : Longint): Integer;
const
BitPenup = $8000;
function FPenUp(X: LongInt): Boolean;
inline(
$58/ { POP AX }
$5A/ { POP DX }
$2D/$00/$80/ { SUB AX,8000H }
$1B/$C0/ { SBB AX,AX }
$40); { INC AX }
const
IDC_Pen = MakeIntResource(32631);
const
IDC_AltSelect = MakeIntResource(32501);
const
rc_WDefault = $FFFF;
rc_Ldefault = $FFFFFFFF;
rc_WDefaultFlags = $8000;
rc_LDefaultFlags = $80000000;
{ Макрос идентификации(входные потоки)}
const
syvhi_Special = 0;
syvhi_ANSI = 1;
syvhi_Gesture = 2;
syvhi_Kanji = 3;
syvhi_Shape = 4;
syvhi_UniCode = 5;
syvhi_VKey = 6;
function FIsSpecial(syv: TSYV): Boolean;
function FIsAnsi(syv: TSYV): Boolean;
function FIsGesture(syv: TSYV): Boolean;
function FIsKanji(syv: TSYV): Boolean;
function FIsShape(syv: TSYV): Boolean;
function FIsUniCode(syv: TSYV): Boolean;
function FIsVKey(syv: TSYV): Boolean;
{ Конвертеры кодировки файла }
function ChSyvToAnsi(syv: TSYV): Byte;
function SyvCharacterToSymbol(c: Char): TSYV;
function SyvKanjiToSymbol(c: Char): TSYV;
{ SYV значения }
const
syv_Null = $00000000;
syv_Unknown = $00000001;
syv_Empty = $00000003;
syv_BeginOr = $00000010;
syv_EndOr = $00000011;
syv_Or = $00000012;
syv_SoftNewLine = $00000020;
syv_SpaceNull = $00010000;
const
syv_KKConvert = $0002FFD4;
syv_Clear = $0002FFD5;
syv_ExtendSelect = $0002FFD8;
syv_Undo = $0002FFD9;
syv_Copy = $0002FFDA;
syv_Cut = $0002FFDB;
syv_Paste = $0002FFDC;
syv_ClearWord = $0002FFDD;
syv_User = $0002FFDE; { Восстановление исходника }
syv_Correct = $0002FFDF;
syv_Backspace = $00020008;
syv_Tab = $00020009;
syv_Return = $0002000D;
syv_Space = $00020020;
function FIsStdGesture(syv: TSYV): Boolean;
function FIsAnsiGesture(syv: TSYV): Boolean;
{ Приложения по подгрузки масок }
const
syv_AppGestureMask = $00020000;
syv_CircleUpA = $000224B6;
syv_CircleUpZ = $000224CF;
syv_CircleLoA = $000224D0;
syv_CircleLoZ = $000224E9;
function FIsLoAppGesture(syv: TSYV): Boolean;
function FIsUpAppGesture(syv: TSYV): Boolean;
function FIsAppGesture(syv: TSYV): Boolean;
function SyvAppGestureFromLoAnsi(Ansi: Char): TSYV;
function SyvAppGestureFromUpAnsi(Ansi: Char): TSYV;
function AnsiFromSyvAppGesture(syv: TSYV): Byte;
{Константы обработки входных значений декодирования}
const
rec_OEM = –1024;
rec_Language = –48;
rec_Guide = –47;
rec_ParamError = –46;
rec_InvalidRef = –45;
rec_RectExclude = –44;
rec_RectBound = –43;
rec_PCM = –42;
rec_ResultMode = –41;
rec_HWnd = –40;
rec_ALC = –39;
rec_ErrorLevel = –38;
rec_CLVerify = –37;
rec_Dict = –36;
rec_HRec = –35;
rec_BadEventRef = –33;
rec_NoCollection = –32;
rec_Debug = –32;
rec_PointerEvent = –31;
rec_BadHPenData = –9;
rec_OOM = –8;
rec_NoInput = –7;
rec_NoTablet = –6;
rec_Busy = –5;
rec_BufferTooSmall = –4;
rec_Abort = –3;
rec_Overflow = –1;
rec_OK = 0;
rec_TermBound = 1;
rec_TermEx = 2;
rec_TermPenUp = 3;
rec_TermRange = 4;
rec_TermTimeOut = 5;
rec_Done = 6;
rec_TermOEM = 512;
type
POEMPenInfo = ^TOEMPenInfo;
TOEMPenInfo = record
wPdt: Word;
wValueMax: Word;
wDistinct: Word;
end;
const
pdt_Null = 0;
pdt_Pressure = 1;
pdt_Height = 2;
pdt_AngleXY = 3;
pdt_AngleZ = 4;
pdt_BarrelRotation = 5;
pdt_OEMSpecific = 16;
MaxOEMDataWords = 6;
type
PPenPacket = ^TPenPacket;
TPenPacket = record
wTabletX: Word;
wTabletY: Word;
wPDK: Word;
rgwOemData: array[0..MaxOEMDataWords – 1] of Word;
end;
type
TRawHook = function(PenPacket: PPenPacket): Bool;
type
PPenInfo = ^TPenInfo;
TPenInfo = record
cxRawWidth: Word;
cyRawHeight: Word;
wDistinctWidth: Word;
wDistinctHeight: Word;
nSamplingRate: Integer;
nSamplingDist: Integer;
lPdc: Longint;
cPens: Integer;
cbOemData: Integer;
rgoempeninfo: array[0..MaxOEMDataWords – 1] of TOEMPenInfo;
rgwReserved: array[0..7] of Word;
end;
const
pdc_Integrated = $00000001;
pdc_Proximity = $00000002;
pdc_Range = $00000004;
pdc_Invert = $00000008;
pdc_Relative = $00000010;
pdc_Barrel1 = $00000020;
pdc_Barrel2 = $00000040;
pdc_Barrel3 = $00000080;
type
PStrokeInfo = ^TStrokeInfo;
TStrokeInfo = record
cPnt: Word;
cbPnts: Word;
wPDK: Word;
dwTick: Longint;
end;
type
PCalbStruct = ^TCalbStruct;
TCalbStruct = record
wOffsetX: Integer;
wOffsetY: Integer;
wDistinctWidth: Integer;
wDistinctHeight: Integer;
end;
const
drv_SetPenDriverEntryPoints = drv_Reserved+1;
drv_RemovePenDriverEntryPoints = drv_Reserved+2;
drv_SetPenSamplingRate = drv_Reserved+3;
drv_SetPenSamplingDist = drv_Reserved+4;
drv_GetCalibration = drv_Reserved+11;
drv_SetCalibration = drv_Reserved+12;
const
pdk_Up = $0000;
pdk_Down = $0001;
pdk_Barrel1 = $0002;
pdk_Barrel2 = $0004;
pdk_Barrel3 = $0008;
pdk_Transition = $0010;
pdk_Inverted = $0080;
pdk_OutOfRange = $4000;
pdk_Driver = $8000;
pdk_TipMask = $0001;
pdk_Switches = pdk_Down or pdk_Barrel1 or pdk_Barrel2 or
pdk_Barrel3;
const
pcm_Penup = $00000001;
pcm_Range = $00000002;
pcm_Invert = $00000020;
pcm_RectExclude = $00002000;
pcm_RectBound = $00004000;
pcm_Timeout = $00008000;
pcm_AddDefaults = rc_LDefaultFlags; { $80000000 }
procedure PostVirtualKeyEvent(vk: Word; fUp: Bool);
procedure PostVirtualMouseEvent(wMouseFlag: Word; xPos, yPos: Integer);
procedure AtomicVirtualEvent(fBegin: Bool);
const
vwm_MouseMove = $0001;
vwm_MouseLeftDown = $0002;
vwm_MouseLeftUp = $0004;
vwm_MouseRightDown = $0008;
vwm_MouseRightUp = $0010;
const
cl_Null = 0;
cl_Minimum = 1;
cl_Maximum = 100;
InkWidth_Minimum = 0;
InkWidth_Maximum = 15;
enum_Minimum = 1;
enum_Maximum = 4096;
MaxDictionaries = 16;
type
PGuide = ^TGuide;
TGuide = record
xOrigin: Integer;
yOrigin: Integer;
cxBox: Integer;
cyBox: Integer;
cxBase: Integer;
cyBase: Integer;
cHorzBox: Integer;
cVertBox: Integer;
cyMid: Integer;
end;
type
TRCYieldProc = function : Bool;
const
cbRcLanguageMax = 44;
cbRcUserMax = 32;
cbRcrgbfAlcMax = 32;
cwRcReservedMax = 8;
type
PRC = ^TRC;
TRC = record
HRec: THRec;
hw: HWnd;
wEventRef: Word;
wRcPreferences: Word;
lRcOptions: Longint;
lpfnYield: TRCYieldProc;
lpUser: array[0..cbRcUserMax–1] of Byte;
wCountry: Word;
wIntlPreferences: Word;
lpLanguage: array[0..cbRcLanguageMax–1] of Char;
rglpdf: array[0..MaxDictionaries–1] of TDF;
wTryDictionary: Word;
clErrorLevel: TCL;
alc: TALC;
alcPriority: TALC;
rgbfAlc: array[0..cbRcrgbfAlcMax–1] of Byte;
wResultMode: Word;
wTimeOut: Word;
lPcm: Longint;
rectBound: TRect;
rectExclude: TRect;
guide: TGuide;
wRcOrient: Word;
wRcDirect: Word;
nInkWidth: Integer;
rgbInk: TColorRef;
dwAppParam: Longint;
dwDictParam: Longint;
dwRecognizer: Longint;
rgwReserved: array[0..cwRcReservedMax–1] of Word;
end;
type
THPenData = THandle;
type
PSYC = ^TSYC;
TSYC = record
wStrokeFirst: Word;
wPntFirst: Word;
wStrokeLast: Word;
wPntLast: Word;
fLastSyc: Bool;
end;
const
wPntAll = $FFFF;
iSycNull = –1;
type
PSYE = ^TSYE;
TSYE = record
syv: TSYV;
lRecogVal: Longint;
cl: TCL;
iSyc: Integer;
end;
const
MaxHotSpot = 8;
type
PSYG = ^TSYG;
TSYG = record
rgpntHotSpots: array[0..MaxHotSpot–1] of TPoint;
cHotSpot: Integer;
nFirstBox: Integer;
lRecogVal: Longint;
lpsye: PSYE;
cSye: Integer;
lpsyc: PSYC;
cSyc: Integer;
end;
type
TEnumProc = function(syv: PSYV; i: Integer; P: Pointer): Integer;
type
PRCResult = ^TRCResult;
TRCResult = record
syg: TSYG;
wResultsType: Word;
cSyv: Integer;
lpsyv: PSYV;
HSyv: THandle;
nBaseLine: Integer;
nMidLine: Integer;
hPenData: THPenData;
rectBoundInk: TRect;
pntEnd: TPoint;
lprc: PRC;
end;
const
rcrt_Default = $0000;
rcrt_Unidentified = $0001;
rcrt_Gesture = $0002;
rcrt_NoSymbolMatch = $0004;
rcrt_Private = $4000;
rcrt_NoRecog = $8000;
rcrt_AlreadyProcessed = $0008;
rcrt_GestureTranslated = $0010;
rcrt_GestureToKeys = $0020;
hkp_SetHook = 0;
hkp_Unhook = $FFFF;
hwr_Results = 0;
hwr_AppWide = 1;
pen_NoInkWidth = 0;
const
rpa_Default = 1;
{ GetGlobalRC возвращает кода}
const
ggrc_OK = 0;
ggrc_DictBufTooSmall = 1;
ggrc_ParamError = 2;
{ SetGlobalRC устанавливает код}
const
sgrc_OK = $0000;
sgrc_User = $0001;
sgrc_ParamError = $0002;
sgrc_RC = $0004;
sgrc_Recognizer = $0008;
sgrc_Dictionary = $0010;
sgrc_INIFile = $0020;
{ Макро }
function GetWEventRef: Word;
function InstallRecognizer(lpszRecogName: PChar): THRec;
procedure UninstallRecognizer(HRec: THRec);
function GetGlobalRC(lprc: PRC; lpDefRecog: PChar; lpDefDict: PChar;
cbDefDictMax: Integer): Word;
function SetGlobalRC(lprc: PRC; lpDefRecog: PChar; lpDefDict: PChar): Word;
procedure RegisterPenApp(wFlags: Word; fRegister: Bool);
function IsPenAware: Word;
function SetRecogHook(whrHook: Word; hkpPosition: Word; HWndHook: HWnd): Bool;
procedure InitRC(hw: HWnd; lprc: PRC);
function Recognize(lprc: PRC): TRec;
function RecognizeData(lprc: PRC; hPenData: THPenData): TRec;
function TrainInk(lprc: PRC; hPenData: THPenData; lpsyv: PSYV): Bool;
function TrainContext(lprcresult: PRCResult; lpsye: PSYE; cSye: Integer;
lpsyc: PSYC; cSyc: Integer): Bool;
function ProcessWriting(hw: HWnd; lprc: PRC): TRec;
function CorrectWriting(hw:HWnd; lpBuf:PChar; cbBuf: Word; lprc: PRC;
dwCwrFlags: Longint; dwReserved: Longint): Bool;
procedure EmulatePen(fPen: Bool);
function GetSymbolMaxLength(lpsyg: PSYG): Integer;
function GetSymbolCount(lpsyg: PSYG): Integer;
procedure FirstSymbolFromGraph(lpsyg: PSYG; lpsyv: PSYV; cSyvMax: Integer;
lpcSyv: PInteger);
function EnumSymbols(lpsyg: PSYG; wMaxStr: Word; lpEnumFunc: TEnumProc;
lvData: Pointer): Word;
function TPtoDP(lpPnt: PPoint; cPnt: Integer): Bool;
function DPtoTP(lpPnt: PPoint; cPnt: Integer): Bool;
procedure BoundingRectFromPoints(lpPnt: PPoint; cPnt: Integer;
lpRectBound: PRect);
function SymbolToCharacter(lpsyv: PSYV; cSyv: Integer; lpstr: PStr;
lpnConv: PInteger): Bool;
function CharacterToSymbol(lpstr: PStr; cSyv: Integer; lpsyv: PSYV): Integer;
function GetVersionPenWin: Word;
function ExecuteGesture(hw: HWnd; syv: TSYV; lprcresult: PRCResult): Bool;
const
alc_All = $000043FF;
alc_Default = $00000000;
alc_LCAlpha = $00000001;
alc_UCAlpha = $00000002;
alc_Alpha = $00000003;
alc_Numeric = $00000004;
alc_Alphanumeric = $00000007;
alc_Punc = $00000008;
alc_Math = $00000010;
alc_Monetary = $00000020;
alc_Other = $00000040;
alc_White = $00000100;
alc_NonPrint = $00000200;
alc_Gesture = $00004000;
alc_UseBitmap = $00008000;
alc_DBCS = $00000400;
alc_Hiragana = $00010000;
alc_Katakana = $00020000;
alc_Kanji = $00040000;
alc_OEM = $0FF80000;
alc_Reserved = $F0003800;
alc_NoPriority = $00000000;
alc_SysMinimum = alc_Alphanumeric or
alc_Punc or alc_White or
alc_Gesture;
{ macros }
function MpAlcB(lprc: PRC; i: Word): PByte;
function MpIbf(i: Word): Byte;
procedure SetAlcBitAnsi(lprc: PRC; i: Word);
procedure ResetAlcBitAnsi(lprc: PRC; i: Word);
function IsAlcBitAnsi(lprc: PRC; i: Word): Boolean;
const
rcd_Default = 0;
rcd_LR = 1;
rcd_RL = 2;
rcd_TB = 3;
rcd_BT = 4;
const
rco_NoPointerEvent = $00000001;
rco_SaveAllData = $00000002;
rco_SaveHPenData = $00000004;
rco_NoFlashUnknown = $00000008;
rco_TabletCoord = $00000010;
rco_NoSpaceBreak = $00000020;
rco_NoHideCursor = $00000040;
rco_NoHook = $00000080;
rco_Boxed = $00000100;
rco_Suggest = $00000200;
rco_DisableGesMap = $00000400;
rco_NoFlashCursor = $00000800;
rco_ColdRecog = $00008000;
const
rcp_LeftHand = $0001;
rcp_MapChar = $0004;
const
rcor_Normal = 1;
rcor_Right = 2;
rcor_Upsidedown = 3;
rcor_Left = 4;
rrm_Stroke = 0;
rrm_Symbol = 1;
rrm_Word = 2;
rrm_NewLine = 3;
rrm_Complete = 16;
rcip_AllAnsiChar = $0001;
rcip_Mask = $0001;
cwr_StripCR = $00000001;
cwr_StripLF = $00000002;
cwr_StripTAB = $00000004;
cwr_SingleLineEdit = $00000007;
cwr_Title = $00000010;
cwr_KKConvert = $00000020;
const
map_GestOGES = rcrt_Gesture or rcrt_GestureTranslated;
map_GestOVKeys = rcrt_GestureToKeys or rcrt_AlreadyProcessed;
{ макросы }
function IsGestureToGesture(lprcresult: PRCResult): Boolean;
function IsGestureToVkeys(lprcresult: PRCResult): Boolean;
procedure SetAlreadyProcessed(lprcresult: PRCResult);
type
PPenDataHeader = ^TPenDataHeader;
TPenDataHeader = record
wVersion: Word;
cbSizeUsed: Word;
cStrokes: Word;
cPnt: Word;
cPntStrokeMax: Word;
rectBound: TRect;
wPndts: Word;
nInkWidth: Integer;
rgbInk: Longint;
end;
const
pdts_LOMetric = $0000;
pdts_HIMetric = $0001;
pdts_HIEnglish = $0002;
pdts_ScaleMax = $0003;
pdts_Display = $0003;
pdts_Arbitrary = $0004;
pdts_ScaleMask = $000F;
pdts_StandardScale = pdts_HIEnglish;
pdts_NoPenInfo = $0100;
pdts_NoUpPoints = $0200;
pdts_NoOEMData = $0400;
pdts_NoColinear = $0800;
pdts_Compressed = $8000;
pdts_CompressMethod = $00F0;
pdts_Compress2ndDeriv = $0010;
pdtt_Default = $0000;
pdtt_PenInfo = pdts_NoPenInfo;
pdtt_UpPoints = pdts_NoUpPoints;
pdtt_OEMdata = pdts_NoOEMData;
pdtt_Colinear = pdts_NoColinear;
pdtt_Compress = pdts_Compressed;
pdtt_Decompress = $4000;
pdtt_All = pdtt_PenInfo or pdtt_UpPoints or pdtt_OEMdata or pdtt_Colinear;
function DestroyPenData(hPenData: THPenData): Boolean;
procedure EndEnumStrokes(hPenData: THPenData);
function IsPenEvent(Message: Word; lExtraInfo: Longint): Bool;
function GetPenAsyncState(wPDK: Word): Bool;
function GetPenDataInfo(hPenData: THPenData; lppendataheader: PPenDataHeader;
lpPenInfo: PPenInfo; dwReserved: Longint): Bool;
function GetPenDataStroke(lppendata: PPenDataHeader; wStroke: Word;
lplpPoint: PPoint; lplpvOem: Pointer; lpsi: PStrokeInfo ): Bool;
function GetPointsFromPenData(hPenData: PPenDataHeader; wStroke, wPnt, cPnt: Word;
lppoint: PPoint): Bool;
procedure DrawPenData(DC: HDC; lprect: PRect; hPenData: THPenData);
function MetricScalePenData(hPenData: THPenData; wPdts: Word): Bool;
function ResizePenData(hPenData: THPenData; lprect: PRect): Bool;
function OffsetPenData(hPenData: THPenData; dx, dy: Integer): Bool;
function RedisplayPenData(DC:HDC; hPenData: THPenData; lpDelta: PPoint;
lpExt: PPoint; nInkWidth: Integer; rgbColor: Longint): Bool;
function CompactPenData(hPenData: THPenData; wTrimOptions: Word): THPenData;
function DuplicatePenData(hPenData:THPenData; gmemFlags: Word): THPenData;
function CreatePenData(lpPenInfo: PPenInfo; cbOemData: Integer;
wPdtScale: Word; gmemFlags: Word): THPenData;
function AddPointsPenData(hPenData: THPenData; lpPnt: PPoint;
lpvOemData: Pointer; lpsiNew: PStrokeInfo): THPenData;
function BeginEnumStrokes(hPenData: THPenData): PPenDataHeader;
function DictionarySearch(lprc: PRC; lpsye: PSYE; cSye: Integer;
lpsyv: PSYV; cSyvMax: Integer): Bool;
const
he_GetRC = 3;
he_SetRC = 4;
he_GetInflate = 5;
he_SetInflate = 6;
he_GetUnderline = 7;
he_SetUnderline = 8;
he_GetInkHandle = 9;
he_SetInkMode = 10;
he_StopInkMode = 11;
he_GetRCResultCode = 12;
he_DefaultFont = 13;
he_CharPosition = 14;
he_CharOffset = 15;
he_GetRCResult = 22;
he_KKConvert = 30;
he_GetKKConvert = 31;
he_CancelKKConvert = 32;
he_FixKKConvert = 33;
hekk_Default = 0;
hekk_Convert = 1;
hekk_Candidate = 2;
hep_NoRecog = 0;
hep_Recog = 1;
hep_WaitForTap = 2;
hn_EndRec = 4;
hn_DelayedRecogFail = 5;
hn_RCResult = 20;
hn_EndKKConvert = 30;
type
PRectOfs = ^TRectOfs;
TRectOfs = record
dLeft: Integer;
dTop: Integer;
dRight: Integer;
dBottom: Integer;
end;
{Конроль за идентификацией данных}
type
PBoxLayout = ^TBoxLayout;
TBoxLayout = record
cyCusp: Integer;
cyEndCusp: Integer;
Style: Word;
rgbText: Longint;
rgbBox: Longint;
rgbSelect: Longint;
end;
const
bxs_None = 0;
bxs_Rect = 1;
bxs_EndTextmark = 2;
bxs_Mask = 3;
he_GetBoxLayout = 20;
he_SetBoxLayout = 21;
bxd_CellWidth = 12;
bxd_CellHeight = 16;
bxd_BaseHeight = 13;
bxd_BaseHorz = 0;
bxd_CuspHeight = 2;
bxd_EndCuspHeight = 4;
function ShowKeyboard(Handle: HWnd; wCommand: Word; lpPnt: PPoint;
lpSKBInfo: PSKBInfo): Bool;
const
cbn_EndRec = 16;
cbn_DelayedRecogFail = 17;
cbn_RcResult = 18;
implementation
type
LongRec = record
Lo, Hi: Word;
end;
WordRec = record
Lo, Hi: Byte;
end;
{ translations of macros }
function ChSyvToAnsi(syv: Longint): Byte;
begin
ChSyvToAnsi := WordRec(LongRec(syv).Lo).Lo;
end;
function SyvCharacterToSymbol(c: Char): Longint;
begin
SyvCharacterToSymbol := Byte(c) or $10000;
end;
function SyvKanjiToSymbol(c: Char): TSYV;
begin
SyvKanjiToSymbol := Byte(c) or $30000;
end;
function FIsStdGesture(syv: Longint): Boolean;
begin
FIsStdGesture := (syv = syv_Clear) or (syv = syv_ExtendSelect) or
(syv = syv_Undo) or (syv = syv_Copy) or (syv = syv_Cut) or
(syv = syv_Paste) or (syv = syv_ClearWord) or (syv = syv_KKConvert) or
(syv = syv_User) or (syv = syv_Correct);
end;
function FIsAnsiGesture(syv: TSYV): Boolean;
begin
FIsAnsiGesture := (syv = syv_Backspace) or (syv = syv_Tab) or
(syv = syv_Return) or (syv = syv_Space);
end;
{ Gesture macros }
function FIsLoAppGesture(syv: Longint): Boolean;
begin
FIsLoAppGesture := (syv >= syv_CircleLoA) and (syv <= syv_CircleLoZ);
end;
function FIsUpAppGesture(syv: Longint): Boolean;
begin
FIsUpAppGesture := (syv >= syv_CircleUpA) and (syv <= syv_CircleUpZ);
end;
function FIsAppGesture(syv: Longint): Boolean;
begin
FIsAppGesture := (syv >= syv_CircleUpA) and (syv <= syv_CircleLoZ);
end;
function SyvAppGestureFromLoAnsi(Ansi: Char): TSYV;
begin
SyvAppGestureFromLoAnsi := Byte( (Ord(Ansi) – Ord('a')) + syv_CircleLoA );
end;
function SyvAppGestureFromUpAnsi(Ansi: Char): TSYV;
begin
SyvAppGestureFromUpAnsi := Byte( (Ord(Ansi) – Ord('A')) + syv_CircleUpA );
end;
function AnsiFromSyvAppGesture(syv: TSYV): Byte;
begin
if FIsUpAppGesture(syv) then syv := syv_CircleUpA – TSYV('A')
else syv := syv_CircleLoA – TSYV('a');
AnsiFromSyvAppGesture := ChSyvToAnsi(syv);
end;
function FIsSpecial(syv: TSYV): Boolean;
begin
FIsSpecial := LongRec(syv).Hi = syvhi_Special;
end;
function FIsAnsi(syv: TSYV): Boolean;
begin
FIsAnsi := LongRec(syv).Hi = syvhi_ANSI;
end;
function FIsGesture(syv: TSYV): Boolean;
begin
FIsGesture := LongRec(syv).Hi = syvhi_Gesture;
end;
function FIsKanji(syv: TSYV): Boolean;
begin
FIsKanji := LongRec(syv).Hi = syvhi_Kanji;
end;
function FIsShape(syv: TSYV): Boolean;
begin
FIsShape := LongRec(syv).Hi = syvhi_Shape;
end;
function FIsUniCode(syv: TSYV): Boolean;
begin
FIsUniCode := LongRec(syv).Hi = syvhi_UniCode;
end;
function FIsVKey(syv: TSYV): Boolean;
begin
FIsVKey := LongRec(syv).Hi = syvhi_VKey;
end;
function GetWEventRef: Word;
var
Result: Longint;
begin
Result := GetMessageExtraInfo;
GetWEventRef := LongRec(Result).Lo;
end;
function MpAlcB(lprc: PRC; i: Word): PByte;
begin
MpAlcB := @lprc^.rgbfAlc[ (i and $FF) shr 3 ];
end;
function MpIbf(i: Word): Byte;
begin
MpIbf := 1 shl (i and 7);
end;
procedure SetAlcBitAnsi(lprc: PRC; i: Word);
var
P: PByte;
begin
P := MpAlcB(lprc, i);
P^ := P^ or MpIbf(i);
end;
procedure ResetAlcBitAnsi(lprc: PRC; i: Word);
var
P: PByte;
begin
P := MpAlcB(lprc, i);
P^ := P^ and not MpIbf(i);
end;
function IsAlcBitAnsi(lprc: PRC; i: Word): Boolean;
begin
IsAlcBitAnsi := MpAlcB(lprc,i)^ and MpIbf(i) <> 0;
end;
function IsGestureToGesture(lprcresult: PRCResult): Boolean;
begin
IsGestureToGesture :=
(lprcresult^.wResultsType and map_GestOGES) = map_GestOGES;
end;
function IsGestureToVkeys(lprcresult: PRCResult): Boolean;
begin
IsGestureToVkeys :=
(lprcresult^.wResultsType and map_GestOVKeys) = map_GestOVKeys;
end;
procedure SetAlreadyProcessed(lprcresult: PRCResult);
begin
lprcresult^.wResultsType :=
(lprcresult^.wResultsType and (not rcrt_GestureToKeys)) or rcrt_AlreadyProcessed;
end;
function DestroyPenData(hPenData: THPenData): Boolean;
begin
DestroyPenData := GlobalFree(hPenData) = 0;
end;
procedure EndEnumStrokes(hPenData: THPenData);
begin
GlobalUnlock(hPenData);
end;
procedure UpdatePenInfo; external 'PENWIN' index 207;
function EndPenCollection; external 'PENWIN' index 137;
function GetPenHwData; external 'PENWIN' index 138;
function GetPenHwEventData; external 'PENWIN' index 139;
function SetPenHook; external 'PENWIN' index 115;
procedure PostVirtualKeyEvent; external 'PENWIN' index 102;
procedure PostVirtualMouseEvent; external 'PENWIN' index 101;
procedure AtomicVirtualEvent; external 'PENWIN' index 104;
function InstallRecognizer; external 'PENWIN' index 14;
procedure UninstallRecognizer; external 'PENWIN' index 15;
function GetGlobalRC; external 'PENWIN' index 151;
function SetGlobalRC; external 'PENWIN' index 150;
procedure RegisterPenApp; external 'PENWIN' index 111;
function IsPenAware; external 'PENWIN' index 110;
function SetRecogHook; external 'PENWIN' index 114;
procedure InitRC; external 'PENWIN' index 10;
function Recognize; external 'PENWIN' index 11;
function RecognizeData; external 'PENWIN' index 12;
function TrainInk; external 'PENWIN' index 16;
function TrainContext; external 'PENWIN' index 17;
function ProcessWriting; external 'PENWIN' index 170;
function CorrectWriting; external 'PENWIN' index 172;
procedure EmulatePen; external 'PENWIN' index 173;
function GetSymbolMaxLength; external 'PENWIN' index 121;
function GetSymbolCount; external 'PENWIN' index 122;
procedure FirstSymbolFromGraph; external 'PENWIN' index 123;
function EnumSymbols; external 'PENWIN' index 124;
function TPtoDP; external 'PENWIN' index 132;
function DPtoTP; external 'PENWIN' index 131;
procedure BoundingRectFromPoints; external 'PENWIN' index 13;
function SymbolToCharacter; external 'PENWIN' index 125;
function CharacterToSymbol; external 'PENWIN' index 126;
function GetVersionPenWin; external 'PENWIN' index 402;
function ExecuteGesture; external 'PENWIN' index 418;
function IsPenEvent; external 'PENWIN' index 135;
function GetPenAsyncState; external 'PENWIN' index 144;
function GetPenDataInfo; external 'PENWIN' index 211;
function GetPenDataStroke; external 'PENWIN' index 219;
function GetPointsFromPenData; external 'PENWIN' index 221;
procedure DrawPenData; external 'PENWIN' index 214;
function MetricScalePenData; external 'PENWIN' index 215;
function ResizePenData; external 'PENWIN' index 222;
function OffsetPenData; external 'PENWIN' index 216;
function RedisplayPenData; external 'PENWIN' index 242;
function CompactPenData; external 'PENWIN' index 223;
function DuplicatePenData; external 'PENWIN' index 218;
function CreatePenData; external 'PENWIN' index 210;
function AddPointsPenData; external 'PENWIN' index 212;
function BeginEnumStrokes; external 'PENWIN' index 213;
function DictionarySearch; external 'PENWIN' index 420;
function ShowKeyboard; external 'PENWIN' index 250;
{$R *.DFM}
const
id_FName = 100;
id_FPath = 101;
id_FList = 102;
id_DList = 103;
const
fsFileSpec = fsFileName + fsExtension;
type
TDWord = record
Lo, Hi: Word;
end;
var
GCaption: PChar;
GFilePath: PChar;
GPathName: array[0..fsPathName] of Char;
GExtension: array[0..fsExtension] of Char;
GFileSpec: array[0..fsFileSpec] of Char;
function GetFileName(FilePath: PChar): PChar;
var
P: PChar;
begin
P := StrRScan(FilePath, '\');
if P = nil then P := StrRScan(FilePath, ':');
if P = nil then GetFileName := FilePath else GetFileName := P + 1;
end;
function GetExtension(FilePath: PChar): PChar;
var
P: PChar;
begin
P := StrScan(GetFileName(FilePath), '.');
if P = nil then GetExtension := StrEnd(FilePath) else GetExtension := P;
end;
function FileDialog(Dialog: HWnd; Message, WParam: Word;
LParam: TDWord): Bool; export;
var
PathLen: Word;
P: PChar;
procedure UpdateFileName;
begin
SetDlgItemText(Dialog, id_FName, StrLower(GPathName));
SendDlgItemMessage(Dialog, id_FName, em_SetSel, 0, $7FFF0000);
end;
procedure SelectFileName;
begin
SendDlgItemMessage(Dialog, id_FName, em_SetSel, 0, $7FFF0000);
SetFocus(GetDlgItem(Dialog, id_FName));
end;
function UpdateListBoxes: Boolean;
var
Result: Integer;
Path: array[0..fsPathName] of Char;
begin
UpdateListBoxes := False;
if GetDlgItem(Dialog, id_FList) <> 0 then
begin
StrCopy(Path, GPathName);
Result := DlgDirList(Dialog, Path, id_FList, id_FPath, 0);
if Result <> 0 then DlgDirList(Dialog, '*.*', id_DList, 0, $C010);
end else
begin
StrLCopy(Path, GPathName, GetFileName(GPathName) – GPathName);
StrLCat(Path, '*.*', fsPathName);
Result := DlgDirList(Dialog, Path, id_DList, id_FPath, $C010);
end;
if Result <> 0 then
begin
StrLCopy(GFileSpec, GetFileName(GPathName), fsFileSpec);
StrCopy(GPathName, GFileSpec);
UpdateFileName;
UpdateListBoxes := True;
end;
end;
begin
FileDialog := True;
case Message of
wm_InitDialog:
begin
SendDlgItemMessage(Dialog, id_FName, em_LimitText, fsPathName, 0);
if GCaption <> nil then SetWindowText(Dialog, GCaption);
StrLCopy(GPathName, GFilePath, fsPathName);
StrLCopy(GExtension, GetExtension(GPathName), fsExtension);
if not UpdateListBoxes then
begin
StrCopy(GPathName, '*.*');
UpdateListBoxes;
end;
SelectFileName;
Exit;
end;
wm_Command:
case WParam of
id_FName:
begin
if LParam.Hi = en_Change then
EnableWindow(GetDlgItem(Dialog, id_Ok),
SendMessage(LParam.lo, wm_GetTextLength, 0, 0) <> 0);
Exit;
end;
id_FList:
if (LParam.Hi = lbn_SelChange) or (LParam.Hi = lbn_DblClk) then
begin
DlgDirSelect(Dialog, GPathName, id_FList);
UpdateFileName;
if LParam.Hi = lbn_DblClk then
SendMessage(Dialog, wm_Command, id_Ok, 0);
Exit;
end;
id_DList:
if (LParam.Hi = lbn_SelChange) or (LParam.Hi = lbn_DblClk) then
begin
DlgDirSelect(Dialog, GPathName, id_DList);
StrCat(GPathName, GFileSpec);
if LParam.Hi = lbn_DblClk then
UpdateListBoxes else
UpdateFileName;
Exit;
end;
id_Ok:
begin
GetDlgItemText(Dialog, id_FName, GPathName, fsPathName + 1);
FileExpand(GPathName, GPathName);
PathLen := StrLen(GPathName);
if (GPathName[PathLen – 1] = '\') or
(StrScan(GPathName, '*') <> nil) or
(StrScan(GPathName, '?') <> nil) or
(GetFocus = GetDlgItem(Dialog, id_DList)) then
begin
if GPathName[PathLen – 1] = '\' then
StrLCat(GPathName, GFileSpec, fsPathName);
if not UpdateListBoxes then
begin
MessageBeep(0);
SelectFileName;
end;
Exit;
end;
StrLCat(StrLCat(GPathName, '\', fsPathName),
GFileSpec, fsPathName);
if UpdateListBoxes then Exit;
GPathName[PathLen] := #0;
if GetExtension(GPathName)[0] = #0 then
StrLCat(GPathName, GExtension, fsPathName);
StrLower(StrCopy(GFilePath, GPathName));
EndDialog(Dialog, 1);
Exit;
end;
id_Cancel:
begin
EndDialog(Dialog, 0);
Exit;
end;
end;
end;
FileDialog := False;
end;
function DoFileDialog(Window: HWnd;
FilePath, DialogName, Caption: PChar): Boolean;
var
DialogProc: TFarProc;
begin
GFilePath := FilePath;
GCaption := Caption;
DialogProc := MakeProcInstance(@FileDialog, HInstance);
DoFileDialog := DialogBox(HInstance, DialogName, Window, DialogProc) = 1;
FreeProcInstance(DialogProc);
end;
function DoFileOpen(Window: HWnd; FilePath: PChar): Boolean;
begin
DoFileOpen := DoFileDialog(Window, FilePath, 'FileOpen', nil);
end;
function DoFileSave(Window: HWnd; FilePath: PChar): Boolean;
begin
DoFileSave := DoFileDialog(Window, FilePath, 'FileSave', nil);
end;
procedure TForm1.Button2Click(Sender: TObject); {ВЫХОД}
begin
close;
end;
procedure TForm1.Button1Click(Sender: TObject); {СПЕКТР. АНАЛ.}
var
i,j,k,n: integer;
sred,otkl:real;
sign:textfile;
mass:array[0..5] of real;
massx,massy:array[1..5,0..5]of real;
s,m:byte;
p,min:real;
mass1: array [1..20,1..20] of word;
mass2: array [1..20,1..20,1..20] of word;
begin
n:= 27;
ind:=0;
assignfile(sign,'sign01.txt');
reset(sign);
progressbar1.StepIt;progressbar1.StepIt;progressbar1.StepIt;progressbar1.StepIt;progressbar1.StepIt;
progressbar1.StepIt;progressbar1.StepIt;progressbar1.StepIt;progressbar1.StepIt;progressbar1.StepIt;
{Весь файл}
for k:=1 to 5 do
begin
{Объект}
for j:=0 to 5 do
begin
{Выборка}
sred:=0;otkl:=0;
for i:=0 to 5 do
begin
read(sign,mass[i]);
sred:=sred+mass[i];
end;
sred:=sred/6;
for i:=0 to 5 do otkl:=otkl+abs(mass[i]–sred);
otkl:=otkl/100+i*0.01;
massx[k,j]:=sred;
massy[k,j]:=otkl;
end;end;close(sign);reset(sign);
for i:=1 to 5 do
for j:=0 to 5 do
begin
read(sign,p)
mass[i,j]:=p*ln(sqrt(otkl)/(1.325113*p/16)–exp(p));
otkl:=1.3*arctg(mass[i,j])+sqr(i–p);
sred:=ln(sqr(p+sred)*456/otkl–mass[i,j]);
mass[i,j]:=mass[i,j]/otkl+ sred;
end;
{cоздание образа}
inc(ind,1);
if ind = 1 then
begin
for i:=0 to 5 do chart1.SeriesList[0].AddXY(massx[1,i],massy[1,i],'',clred);
for i:=0 to 5 do chart1.SeriesList[1].AddXY(massx[2,i],massy[2,i],'',clred);
for i:=0 to 5 do chart1.SeriesList[2].AddXY(massx[3,i],massy[3,i],'',clred);
for i:=0 to 5 do chart1.SeriesList[3].AddXY(massx[4,i],massy[4,i],'',clred);
for i:=0 to 5 do chart1.SeriesList[4].AddXY(massx[5,i],massy[5,i],'',clred);
for i:=0 to 5 do begin
chart1.SeriesList[5].AddXY(massx[1,i],massy[1,i],'',clred);
chart1.SeriesList[5].AddXY(massx[2,i],massy[2,i],'',clred);
end;
for i:=0 to 5 do begin
chart1.SeriesList[6].AddXY(massx[1,i],massy[1,i],'',clred);
chart1.SeriesList[6].AddXY(massx[3,i],massy[3,i],'',clred);
end;
for i:=0 to 5 do begin
chart1.SeriesList[7].AddXY(massx[1,i],massy[1,i],'',clred);
chart1.SeriesList[7].AddXY(massx[4,i],massy[4,i],'',clred);
end;
for i:=0 to 5 do begin
chart1.SeriesList[8].AddXY(massx[1,i],massy[1,i],'',clred);
chart1.SeriesList[8].AddXY(massx[5,i],massy[5,i],'',clred);
end;
for i:=0 to 5 do begin
chart1.SeriesList[9].AddXY(massx[2,i],massy[2,i],'',clred);
chart1.SeriesList[9].AddXY(massx[3,i],massy[3,i],'',clred);
end;
for i:=0 to 5 do begin
chart1.SeriesList[10].AddXY(massx[2,i],massy[2,i],'',clred);
chart1.SeriesList[10].AddXY(massx[4,i],massy[4,i],'',clred);
end;
for i:=0 to 5 do begin
chart1.SeriesList[11].AddXY(massx[2,i],massy[2,i],'',clred);
chart1.SeriesList[11].AddXY(massx[5,i],massy[5,i],'',clred);
end;
for i:=0 to 5 do begin
chart1.SeriesList[12].AddXY(massx[3,i],massy[3,i],'',clred);
chart1.SeriesList[12].AddXY(massx[4,i],massy[4,i],'',clred);
end;
for i:=0 to 5 do begin
chart1.SeriesList[13].AddXY(massx[3,i],massy[3,i],'',clred);
chart1.SeriesList[13].AddXY(massx[5,i],massy[5,i],'',clred);
end;
for i:=0 to 5 do begin
chart1.SeriesList[14].AddXY(massx[4,i],massy[4,i],'',clred);
chart1.SeriesList[14].AddXY(massx[5,i],massy[5,i],'',clred);
end;
for i:=0 to 5 do begin
chart1.SeriesList[15].AddXY(massx[1,i],massy[1,i],'',clred);
chart1.SeriesList[15].AddXY(massx[2,i],massy[2,i],'',clred);
chart1.SeriesList[15].AddXY(massx[3,i],massy[3,i],'',clred);
end;
for i:=0 to 5 do begin
chart1.SeriesList[16].AddXY(massx[1,i],massy[1,i],'',clred);
chart1.SeriesList[16].AddXY(massx[2,i],massy[2,i],'',clred);
chart1.SeriesList[16].AddXY(massx[4,i],massy[4,i],'',clred);
end;
for i:=0 to 5 do begin
chart1.SeriesList[17].AddXY(massx[1,i],massy[1,i],'',clred);
chart1.SeriesList[17].AddXY(massx[2,i],massy[2,i],'',clred);
chart1.SeriesList[17].AddXY(massx[5,i],massy[5,i],'',clred);
end;
for i:=0 to 5 do begin
chart1.SeriesList[18].AddXY(massx[1,i],massy[1,i],'',clred);
chart1.SeriesList[18].AddXY(massx[3,i],massy[3,i],'',clred);
chart1.SeriesList[18].AddXY(massx[4,i],massy[4,i],'',clred);
end;
for i:=0 to 5 do begin
chart1.SeriesList[19].AddXY(massx[1,i],massy[1,i],'',clred);
chart1.SeriesList[19].AddXY(massx[3,i],massy[3,i],'',clred);
chart1.SeriesList[19].AddXY(massx[5,i],massy[5,i],'',clred);
end;
for i:=0 to 5 do begin
chart1.SeriesList[20].AddXY(massx[1,i],massy[1,i],'',clred);
chart1.SeriesList[20].AddXY(massx[4,i],massy[4,i],'',clred);
chart1.SeriesList[20].AddXY(massx[5,i],massy[5,i],'',clred);
end;
for i:=0 to 5 do begin
chart1.SeriesList[21].AddXY(massx[2,i],massy[2,i],'',clred);
chart1.SeriesList[21].AddXY(massx[3,i],massy[3,i],'',clred);
chart1.SeriesList[21].AddXY(massx[4,i],massy[4,i],'',clred);
end;
for i:=0 to 5 do begin
chart1.SeriesList[22].AddXY(massx[2,i],massy[2,i],'',clred);
chart1.SeriesList[22].AddXY(massx[3,i],massy[3,i],'',clred);
chart1.SeriesList[22].AddXY(massx[5,i],massy[5,i],'',clred);
end;
for i:=0 to 5 do begin
chart1.SeriesList[23].AddXY(massx[2,i],massy[2,i],'',clred);
chart1.SeriesList[23].AddXY(massx[4,i],massy[4,i],'',clred);
chart1.SeriesList[23].AddXY(massx[5,i],massy[5,i],'',clred);
end;
for i:=0 to 5 do begin
chart1.SeriesList[24].AddXY(massx[3,i],massy[3,i],'',clred);
chart1.SeriesList[24].AddXY(massx[4,i],massy[4,i],'',clred);
chart1.SeriesList[24].AddXY(massx[5,i],massy[5,i],'',clred);
end;
for i:=0 to 5 do begin
chart1.SeriesList[25].AddXY(massx[1,i],massy[1,i],'',clred);
chart1.SeriesList[25].AddXY(massx[2,i],massy[2,i],'',clred);
chart1.SeriesList[25].AddXY(massx[3,i],massy[3,i],'',clred);
chart1.SeriesList[25].AddXY(massx[4,i],massy[4,i],'',clred);
end;
for i:=0 to 5 do begin
chart1.SeriesList[26].AddXY(massx[1,i],massy[1,i],'',clred);
chart1.SeriesList[26].AddXY(massx[2,i],massy[2,i],'',clred);
chart1.SeriesList[26].AddXY(massx[3,i],massy[3,i],'',clred);
chart1.SeriesList[26].AddXY(massx[5,i],massy[5,i],'',clred);
end;
for i:=0 to 5 do begin
chart1.SeriesList[27].AddXY(massx[1,i],massy[1,i],'',clred);
chart1.SeriesList[27].AddXY(massx[2,i],massy[2,i],'',clred);
chart1.SeriesList[27].AddXY(massx[3,i],massy[3,i],'',clred);
chart1.SeriesList[27].AddXY(massx[4,i],massy[4,i],'',clred);
chart1.SeriesList[27].AddXY(massx[5,i],massy[5,i],'',clred);
end;
end;
{система перегруппировки}
for i:=0 to n do chart1.SeriesList[i].Active:=false;
if checkbox1.Checked=true then
begin
for i:=0 to n do chart1.SeriesList[i].Active:=false;
chart1.SeriesList[0].Active:=true;
end;
if checkbox2.Checked=true then
begin
for i:=0 to n do chart1.SeriesList[i].Active:=false;
chart1.SeriesList[1].Active:=true;
end;
if checkbox3.Checked=true then
begin
for i:=0 to n do chart1.SeriesList[i].Active:=false;
chart1.SeriesList[2].Active:=true;
end;
if checkbox4.Checked=true then
begin
for i:=0 to n do chart1.SeriesList[i].Active:=false;
chart1.SeriesList[3].Active:=true;
end;
if checkbox5.Checked=true then
begin
for i:=0 to n do chart1.SeriesList[i].Active:=false;
chart1.SeriesList[4].Active:=true;
end;
if ((checkbox1.Checked=true)and(checkbox2.Checked=true)) then
begin
for i:=0 to n do chart1.SeriesList[i].Active:=false;
chart1.SeriesList[5].Active:=true;
end;
if ((checkbox1.Checked=true) and (checkbox3.Checked=true)) then
begin
for i:=0 to n do chart1.SeriesList[i].Active:=false;
chart1.SeriesList[6].Active:=true;
end;
if ((checkbox1.Checked=true) and (checkbox4.Checked=true)) then
begin
for i:=0 to n do chart1.SeriesList[i].Active:=false;
chart1.SeriesList[7].Active:=true;
end;
if ((checkbox1.Checked=true) and (checkbox5.Checked=true)) then
begin
for i:=0 to n do chart1.SeriesList[i].Active:=false;
chart1.SeriesList[8].Active:=true;
end;
if ((checkbox2.Checked=true) and (checkbox3.Checked=true)) then
begin
for i:=0 to n do chart1.SeriesList[i].Active:=false;
chart1.SeriesList[9].Active:=true;
end;
if ((checkbox2.Checked=true) and (checkbox4.Checked=true)) then
begin
for i:=0 to n do chart1.SeriesList[i].Active:=false;
chart1.SeriesList[10].Active:=true;
end;
if ((checkbox2.Checked=true) and (checkbox5.Checked=true)) then
begin
for i:=0 to n do chart1.SeriesList[i].Active:=false;
chart1.SeriesList[11].Active:=true;
end;
if ((checkbox3.Checked=true) and (checkbox4.Checked=true)) then
begin
for i:=0 to n do chart1.SeriesList[i].Active:=false;
chart1.SeriesList[12].Active:=true;
end;
if ((checkbox3.Checked=true) and (checkbox5.Checked=true)) then
begin
for i:=0 to n do chart1.SeriesList[i].Active:=false;
chart1.SeriesList[13].Active:=true;
end;
if ((checkbox4.Checked=true) and (checkbox5.Checked=true)) then
begin
for i:=0 to n do chart1.SeriesList[i].Active:=false;
chart1.SeriesList[14].Active:=true;
end;
if ((checkbox1.Checked=true) and (checkbox2.Checked=true) and (checkbox3.Checked=true)) then
begin
for i:=0 to n do chart1.SeriesList[i].Active:=false;
chart1.SeriesList[15].Active:=true;
end;
if ((checkbox1.Checked=true) and (checkbox2.Checked=true) and (checkbox4.Checked=true)) then
begin
for i:=0 to n do chart1.SeriesList[i].Active:=false;
chart1.SeriesList[16].Active:=true;
end;
if ((checkbox1.Checked=true) and (checkbox2.Checked=true) and (checkbox5.Checked=true)) then
begin
for i:=0 to n do chart1.SeriesList[i].Active:=false;
chart1.SeriesList[17].Active:=true;
end;
if ((checkbox1.Checked=true) and (checkbox3.Checked=true) and (checkbox4.Checked=true)) then
begin
for i:=0 to n do chart1.SeriesList[i].Active:=false;
chart1.SeriesList[18].Active:=true;
end;
if ((checkbox1.Checked=true) and (checkbox3.Checked=true) and (checkbox5.Checked=true)) then
begin
for i:=0 to n do chart1.SeriesList[i].Active:=false;
chart1.SeriesList[19].Active:=true;
end;
if ((checkbox1.Checked=true) and (checkbox4.Checked=true) and (checkbox5.Checked=true)) then
begin
for i:=0 to n do chart1.SeriesList[i].Active:=false;
chart1.SeriesList[20].Active:=true;
end;
if ((checkbox2.Checked=true) and (checkbox3.Checked=true) and (checkbox4.Checked=true)) then
begin
for i:=0 to n do chart1.SeriesList[i].Active:=false;
chart1.SeriesList[21].Active:=true;
end;
if ((checkbox2.Checked=true) and (checkbox3.Checked=true) and (checkbox5.Checked=true)) then
begin
for i:=0 to n do chart1.SeriesList[i].Active:=false;
chart1.SeriesList[22].Active:=true;
end;
if ((checkbox2.Checked=true) and (checkbox4.Checked=true) and (checkbox5.Checked=true)) then
begin
for i:=0 to n do chart1.SeriesList[i].Active:=false;
chart1.SeriesList[23].Active:=true;
end;
if ((checkbox3.Checked=true) and (checkbox4.Checked=true) and (checkbox5.Checked=true)) then
begin
for i:=0 to n do chart1.SeriesList[i].Active:=false;
chart1.SeriesList[24].Active:=true;
end;
if ((checkbox1.Checked=true) and (checkbox2.Checked=true) and (checkbox3.Checked=true)and (checkbox4.Checked=true)) then
begin
for i:=0 to n do chart1.SeriesList[i].Active:=false;
chart1.SeriesList[25].Active:=true;
end;
if ((checkbox1.Checked=true) and (checkbox2.Checked=true) and (checkbox3.Checked=true)and (checkbox5.Checked=true)) then
begin
for i:=0 to n do chart1.SeriesList[i].Active:=false;
chart1.SeriesList[26].Active:=true;
end;
if ((checkbox1.Checked=true) and (checkbox2.Checked=true) and
(checkbox3.Checked=true)and (checkbox4.Checked=true)and (checkbox5.Checked=true)) then
begin
for i:=0 to n do chart1.SeriesList[i].Active:=false;
chart1.SeriesList[27].Active:=true;
end;
end;
procedure TForm1.Button3Click(Sender: TObject);
var q:byte;
x1,x2,x3,x_1,x_2,x_3:real;
a1,b1,c1,a2,b2,c2,a3,b3,c3:real;
y1,y2,y3:real;
y,x:array[0..10]of real;
k:array[0..3]of real;
h:real;
i,j:integer;
begin
for i:=0 to 16 do
begin
x1:=1.9;x2:=9.7;x3:=–1.4;a1:=7.6;a2:=2.2;
a3:=–1.3;b1:=0.5;b2:=9.1;b3:=0.2;c1:=2.4;
c2:=4.4;c3:=5.8;y1:=1.9;y2:=9.7;y3:=–1.4;
x_1:=1/a1*(y1–b1*x2–c1*x3);
x_2:=1/b2*(y2–a2*x_1–c2*x3);
x_3:=1/c3*(y3–a3*x_1–b3*x_2);
x1:=x_1;x2:=x_2;x3:=x_3;
k[0]:=h*(x[i]+y[i]);
k[1]:=h*x[i]+h/2*y[i]+k[0]/2;
k[2]:=h*x[i]+h/2–y[i]+k[1]/2;
k[3]:=h*x[i]+h*y[i]+k[2];
y[i+1]:=y[i]+1/6*(k[0]+2*k[1]+2*k[2]+k[3]);
end;
for q:=0 to 24 do
chart1.SeriesList[q].Active:=true;
end;
end.
Все функции программы реализованы следующими подпрограммами:
1) Ввод данных (принятого сигнала);
2) Обработка сигнала;
3) Алгоритм селекции;
4) Вывод результатов (классификация).
Каждая подпрограмма осуществлять некоторый набор функций.
Подпрограмма ввода данных выполняет следующие функции:
– ввод исходных данных;
Подпрограмма обработка данных;
– создание базы типовых характеристик;
Подпрограмма алгоритм селекции:
– сравнение характеристик сигнала с эталонными;
Подпрограмма вывода:
– присвоение класса сигналу и визуализация результатов.
Все функции выполняются в диалоговом режиме.
Для работы с программой требуется один человек. Необходимо знание ПК.
Требования к безопасности КПС включает в себя: основные правила, нормы и условия по технике безопасности, пожарной безопасности и промышленной санитарии, обеспечивающие безопасные условия работы. Безопасность КПС соответствует требованиям, предъявляемым следующими нормативными документами: ГОСТ 12.1.019–79 «ССБТ. Электробезопасность. Общие требования и номенклатура видов защиты», ГОСТ 12.1.045, ГОСТ 12.1.030–81 «ССБТ. Электробезопасность. Заземление. Зануление.»
Комплекс программных средств соответствовует требованиям по эргономике и технической эстетике, то есть:
– отсутствие на рабочем месте посторонних предметов;
– необходимому уровню обеспечения освещенности помещения;
– удобству рабочего места с соблюдением анатомических пропорций человека;
– соблюдением санитарно–технических условий труда.
Требования нормируются системой ГОСТ ССБТ.
В качестве исходных данных используется:
– детерминированный информационный сигнал;
Промежуточные выходные данные:
– дисперсия;
– среднеквадратичное отклонение;
– математическое ожидание;
Выходные данные:
Наибольшая вероятность отнесение классифицируемого объекта к эталонному.
Заключение
В данной работе был проведен анализ и получены следующие результаты:
Проведен анализ физических предпосылок селекции движущихся МНЦ по спектральным параметрам. Разработка алгоритмов и устройств обнаружения МНЦ и оценка их эффективности.
Разработан алгоритм обнаружения МНЦ и оценена их эффективности.
Синтезирован алгоритм классификации движущихся МНЦ и оценена их эффективности.
Разработана система интеллектуального распознавания классов движущихся и селекции неподвижных МНЦ на фоне подстилающей поверхности в интересах построения РЛС разведки и целеуказания повышенной информативности.
Применяемые методы исследования –
методологической основой развиваемых методов, алгоритмов и разрабатываемых устройств служат:
1.
Элементы теории вероятностей, математической статистики и случайных процессов;
2.
Методы статистической теории обнаружения и классификации случайных сигналов;
3.
Методы статистической теории радиолокации;
4.
Методы радиофизики, электродинамики и теории распространения радиоволн.
В рамках научно–технической задачи, решаемой в работе получены следующие результаты:
– разработана математическая модель.
– разработано информационное обеспечение.
– оценена эффективность полученных алгоритмов.
– разработано программное обеспечение.
На защиту выносятся следующие вопросы,
соответствующие основе рассматриваемой задачи.
4. Совокупность аналитических соотношений для вероятностных характеристик поляризационных параметров сигналов, отраженных от МНЦ, наблюдаемых на фоне мешающих отражений.
5. Алгоритмы обнаружения сигналов, отраженных от неподвижных МНЦ, по поляризационным и корреляционным свойствам.
6. Алгоритмы распознавания классов движущихся МНЦ, методика оценки их эффективности.
Практическая значимость работы
состоит в следующем:
4. В разработке программного комплекса для определения спектральных и поляризационных характеристик реальных целей.
5. В получении данных о спектральных свойствах и ПХ МНЦ, позволяющих осуществлять анализ эффективности радиолокационных систем разведки и целеуказания.
6. В разработке методов поляризационной селекции неподвижных МНЦ, наблюдаемых на фоне подстилающей поверхности и местных предметов.
Достоверность результатов диссертационной работы
определяется следующими факторами:
1. В основе исследований, проведенных в работе, лежат хорошо апробированные ранее положения статистической теории радиолокации. Обработка данных и сопоставление их с теоретическими базируется на методах математической статистики.
Литература
1. Белецкий Н.Г. Разделяющие возможности комитетов с различными логиками. – Свердловск: УНЦ АН СССР, 1984. – 23с.
2. Белецкий Н.Г. Модели комитетных алгоритмов распознавания образов // Мат. Методы планирования пром. Производства. – Свердловск: УНЦ АН СССР, 1984. – С. 91–95.
3. Вапник В.Н., Червоненкис А.Я. Теория распознавания образов. – М.: Наука, 1974.
4. Еремин И.И. О несовместных системах линейных неравенств. // ДАН СССР. – 1961. – Т. 138, №6. – С. 1280–1283.
5. Еремин И.И. Итеративный метод для чебышевских приближений несовместных систем линейных неравенств // ДАН СССР. – 1962. – Т.143,№6. – С.1253–1256.
6. Еремин И.И. О задачах выпуклого программирования с противоречивыми ограничениями // Кибернетика.–1971.–№4.–С. 124–129.
7. Еремин И.И., Мазуров Вл.Д. Нестационарные процессы математического программирования.–М.: Наука, 1979.
8. Журавлев Ю.И. Корректные алгебры над множествами некоторых (эвристических) алгоритмов. I–III// Кибернетика.–1977.–№4.–С. 14–21; 1977.–№6.–С. 21–27; 1978.–№2.–С. 35–43.
9. Казанцев В.С. Алгоритм таксономии, основанный на использовании линейных неравенств // Методы для нестационарных задач математического программирования. – Свердловск: УНЦ АН СССР, 1979.–С. 120–125.
10. Кривоногов А.И. Некоторые вопросы обоснования комитетных алгоритмов //Классификация и оптимизация в задачах управления. – Свердловск: УНЦ АН СССР, 1981.–С. 39–51.
11. Кривоногов А.И., Мазуров Вл.Д. Метод комитетов для задач оптимизации и диагностики технико–экономических систем. – Свердловск: УНЦ АН СССР 1985.
12. Мазуров Вл.Д. О комитете системы выпуклых неравенств. – Труды ICM. – 1966, М.:МГУ, 1966. – №14. – С. 41.
13. Мазуров Вл.Д. О построении комитета системы выпуклых неравенств // Кибернетика. – 1967. – №2. – С. 56–59.
14. Мазуров Вл.Д. Об одном методе обучения машины интерпритации геофизических данных // Применение математических методов в горнорудной и металлургической промышленности. – Свердловск: СОМИ АН СССР, 1968. – С. 3–8.
15. Мазуров Вл.Д. Об одном методе обучения узнаванию // Кибернетика. – 1970. – №2. – С. 92–94.
16. Мазуров Вл.Д. Распознавание образов как средство автоматического выбора процедуры в вычислительных методах // ЖВМиМФ. – 1970. – Т. 10, №6. – С. 1520–1525.
17. Мазуров Вл.Д. Комитеты систем неравенств и задача распознавания // Кибернетика. – 1971. – №3. – С. 140–146.
18. Мазуров Вл.Д. О системах неравенств сопряженного вида // Методы выпуклого программирования и приложения. – Свердловск: УНЦ АН СССР, 1973. – С. 42–46.
19. Мазуров Вл.Д. Теория линейных неравенств и распознавание образов // Методы фейеровского типа в выпуклом программировании. – Свердловск: УНЦ АН СССР, 1975. – С. 9–39.
20. Мазуров Вл.Д. Теория и приложения комитетных конструкций // Методы для нестационарных задач математического программирования. – Свердловск: УНЦ АН СССР, 1979. – С. 31–63.
21. Мазуров Вл.Д., Казанцев В.С., Белецкий Н.Г. и др. Пакет КВАЗАР прикладных программ распознавания образов: информ. материалы по мат. обеспечению. – Свердловск: УНЦ АН СССР, 1979.
22. Мазуров Вл.Д., Кривоногов А.И., Казанцев В.С., Сачков Н.О., Белецкий Н.Г. Комитеты в принятии решений // Кибернетика. – 1984. – №1. – С. 90–95.
23. Нильсон Н. Обучающиеся машины. М.: Мир, 1968.
24. Сачков Н.О. Решение смешанных систем неравенств // Методы оптимизации и распознавания образов в задачах управления. – Свердловск: УНЦ АН СССР, 1980. – С. 99–105.
25. Черников С.Н. Линейные неравенства. – М.: Наука, 1968.
26. Черников С.Н. Свертывание конечных систем линейных неравенств // ДАН УССР. – 1969. – №1. – С. 32–35.
27. Ablow C.M., Kaylor D.J. Inconsistent homogenous linear inequalities // Bull. Amer. Math. Soc. – 1965. – V. 71, №5.
28. Monjardet B. An axiomatic theory of tornament aggregation // Mathematics Oper. Res. – 1978. – V.3, №4.
29. Андреев В.В. К вопросу об определении информативности признаков в задачах принятия решений // Метод комитетов в распознавании образов. – Свердловск: УНЦ АН СССР, 1974. – С. 81–94.
30. Горелик А.Л., Гуревич И.Б., Скрипкин В.А. Современное состояние проблемы распознавания. – М.: Радио и связь, 1985.
31. Журавлев Ю.И. и др. Задачи распознавания и классификации со стандартной обучющей информацией // ЖВМиМФ. – 1980. – Т. 20, №5. – С. 1294–1309.
|