|
КУРСОВАЯ работа
Расчет напряжений деформаций в изотропном теле по заданному тензору напряжений
1. Исходные данные
1. Задан следующий тензор напряжений:
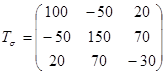 МПа.
МПа.
2. Направляющие косинусы площадки, по которой нужно вычислить напряжения, равны:
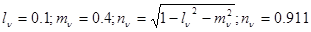 .
.
Инвариантом называется величина, независящая от системы координат. В частности, напряженное состояние в любой точке является инвариантом, несмотря на то, что составляющие тензора в разных системах координат, т.е. напряжения, действующие по координатным площадкам, различны. Однако, имеются выражения, составленные из напряжений по координатным площадкам, которые остаются постоянными в любой системе координат. Эти выражения и называются инвариантами напряженного состояния в точке или инвариантами тензора напряжений.
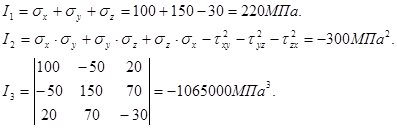 (
1) (
1)
1.2 Определение главных напряжений
Главными напряжениями называются нормальные напряжения, действующие по площадкам, где отсутствуют касательные напряжения. Координатные оси, являющиеся нормалями к таким площадкам, называются главными осями тензора напряжений, а сами площадки – главными площадками.
Главные напряжения определяются из кубичного уравнения:
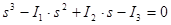 (2) (2)
Подставляя численные значения инвариантов тензора напряжений из(1), получаем:

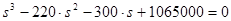
Кубические уравнения общего вида могут иметь комплексные корни, уравнения для определения главных напряжений и главных деформаций всегда имеют три действительных корня. Решать их можно по-разному.
1. Можно сначала определить подбором один из корней уравнения, а затем разложить левую часть уравнения (2) на два сомножителя: линейный двучлен и квадратный трехчлен. После этого из решения квадратного уравнения определяются два оставшиеся корня.
2. Существует и аналитический способ решения, для этого используются формулы Кардано.
Воспользуемся вторым способом.
Пусть задано кубическое уравнения:
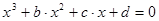 (3)
(3)
После подстановки
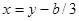 (4) (4)
получим кубичное уравнение (приведенное):
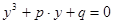 (5) (5)
Здесь 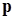 и и 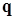 вычисляются по формулам: вычисляются по формулам:
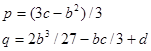 (6) (6)
Формулы Кардано для случая уравнения с тремя действительными корнями имеют вид:
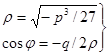 (7) (7)
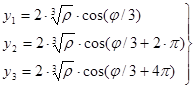 (8) (8)
Далее с помощью подстановки(4) в (3) находим корни исходного уравнения.
Решим наше уравнение (2):
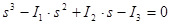 (9)
(9)
Подстановка (4) с новыми обозначениями получает вид:
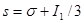 . (10) . (10)
Здесь изменен знак второго слагаемого подстановки потому, что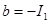 .
.
Подставляя (10) в (9) получим уравнение аналогичное (5):
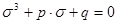 (11) (11)
Здесь коэффициенты 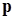 и и 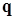 вычисляются по формулам (6): вычисляются по формулам (6):
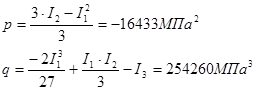
Далее по формулам (7) находим:
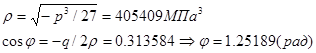
По формулам (8) находим корни уравнения (5):
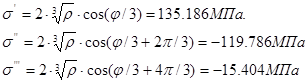
Учитывая (10), находим корни исходного уравнения (9), являющимися главными напряжениями:
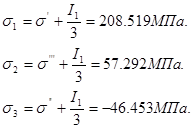 (12) (12)
В соответствии с правилом индексации главных напряжений введены обозначения: 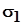 - алгебраически максимальное напряжение; - алгебраически максимальное напряжение; 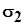 - алгебраически среднее (минимаксное) напряжение; - алгебраически среднее (минимаксное) напряжение; 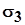 - алгебраически минимальное напряжение. - алгебраически минимальное напряжение.
Величины 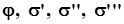 и и 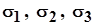 вычислялись с точностью до третьего знака после запятой для того, чтобы в дальнейшем при решении систем уравнений, в которых от вычислялись с точностью до третьего знака после запятой для того, чтобы в дальнейшем при решении систем уравнений, в которых от 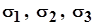 зависят величины коэффициентов, избежать возможных больших погрешностей, если встретятся малые разности больших величин. зависят величины коэффициентов, избежать возможных больших погрешностей, если встретятся малые разности больших величин.
Тензор напряжений в главных осях имеет вид:
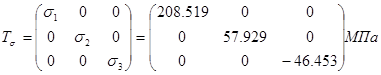 . .
Положение главных осей тензора напряжений определяется матрицей направляющих косинусов:
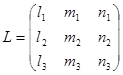 (13) (13)
Здесь первая строка матрицы представляет направляющие косинусы главной оси, по которой действует напряжение 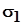 ; вторая строка - направляющие косинусы главной оси, по которой действует напряжение ; вторая строка - направляющие косинусы главной оси, по которой действует напряжение 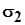 ; третья строка - направляющие косинусы главной оси, по которой действует напряжение ; третья строка - направляющие косинусы главной оси, по которой действует напряжение 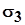 . Все направляющие косинусы задаются в исходной (старой) системе координат, показанной на рис. 1 . Все направляющие косинусы задаются в исходной (старой) системе координат, показанной на рис. 1
Направляющие косинусы главных осей находятся из системы уравнений:
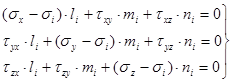 (14) (14)
при условии
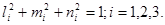 (15) (15)
Здесь 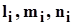 - направляющие косинусы главной оси тензора напряжений, вдоль которой действует напряжение - направляющие косинусы главной оси тензора напряжений, вдоль которой действует напряжение 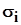 . .
В теории упругости (1) доказывается, что определитель, составленный из коэффициентов при неизвестных (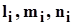 ) системы уравнений (13), равен нулю. Следовательно, три уравнения в (13) являются линейно зависимые: одно уравнение (любое) является следствием двух других. Поэтому для определения направляющих косинусов ) системы уравнений (13), равен нулю. Следовательно, три уравнения в (13) являются линейно зависимые: одно уравнение (любое) является следствием двух других. Поэтому для определения направляющих косинусов 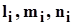 любой главной оси нужно одно из уравнений удалить (любое) и к двум оставшимся добавить уравнение (14). Решив полученную систему трех уравнений с тремя неизвестными, найдем направляющие косинусы любой главной оси нужно одно из уравнений удалить (любое) и к двум оставшимся добавить уравнение (14). Решив полученную систему трех уравнений с тремя неизвестными, найдем направляющие косинусы 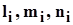 , соответствующие главному напряжению , соответствующие главному напряжению 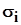 . Положение оставшихся двух осей находят аналогично. . Положение оставшихся двух осей находят аналогично.
Нужно иметь в виду, что каждый из направляющих косинусов получается с двумя знаками. Знаки соответствуют повороту осей по часовой стрелке или против часовой стрелки. При этом главные оси занимают одно и то же положение, но направлены в противоположные стороны.
При определении положения главных осей нужно оставить одну систему знаков, конкретизировав при этом направления осей.
Для определения направляющих косинусов 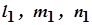 , соответствующих оси, вдоль которой действует напряжение , соответствующих оси, вдоль которой действует напряжение 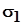 , подставим в (14) и (15) , подставим в (14) и (15) 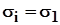 ; при этом из (14) возьмем первые два уравнения (можно взять любые два): ; при этом из (14) возьмем первые два уравнения (можно взять любые два):
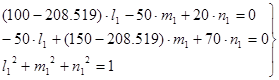 (16) (16)
Сначала найдем отношения между направляющими косинусами; для этого систему уравнений приведем к виду:
 (17) (17)
Решая подсистему, состоящую из первых двух уравнений, получим:
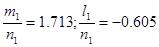 . (18) . (18)
Подставляя эти выражения в третье уравнение (17), найдем:
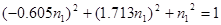 , (19) , (19)
откуда
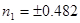 . .
На этом этапе решения задачи можно у 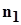 выбрать любой знак. Примем выбрать любой знак. Примем 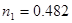 . Подставляя это значение в (18), получим: . Подставляя это значение в (18), получим:
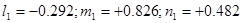 . (20) . (20)
Углы, которые составляет первая главная ось тензора напряжений с исходными осями координат, находятся вычислением функции 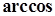 от от 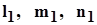 : :
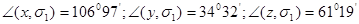 . .
Вычисление 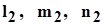
Подставляя в (14) и (15) 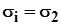 и используя те же два уравнения из (14) (можно и другие), получим: и используя те же два уравнения из (14) (можно и другие), получим:
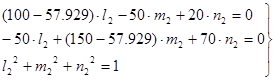 (21) (21)
Решая эту систему уравнений в той же последовательности, как и в п. 3.2.1, получим:
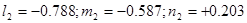 . .
Здесь по-прежнему знак у 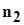 принят положительным, а знаки остальных направляющих косинусов определились решением подсистемы из первых двух уравнений (21). принят положительным, а знаки остальных направляющих косинусов определились решением подсистемы из первых двух уравнений (21).
Углы, которые составляет вторая главная ось с исходными осями координат, пока вычислять не будем. Может оказаться, что определитель матрицы направляющих косинусов будет равен -1
, что соответствует левой системе координат. Для тог, чтобы получить правую систему координат, нужно будет у одной из осей поменять знаки направляющих косинусов.
Подставляя в (14) и (15) 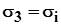 и используя те же уравнения, получим: и используя те же уравнения, получим:
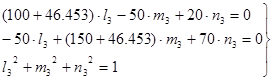 (22) (22)
Решая эту систему, получим:
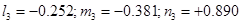 . .
Соответствующие углы равны:
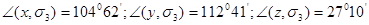 . .
1.4 Проверка правильности вычисления главных напряжений и положения главных осей тензора напряжений
Проверка правильности вычисления главных напряжений
Для проверки правильности вычисленных главных напряжений определим инварианты тензора напряжений:
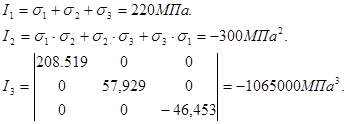
Как видим, инварианты получились такими же, как и в выражениях (1). Этот результат также подтверждает вывод о том, что напряженное состояние в точке нагруженного тела является инвариантным объектом.
Проверка правильности вычисления положения главных осей тензора напряжений
Проверка правильности вычисления положения главных осей тензора напряжений основана на свойствах матрицы направляющих косинусов (13). Она относится к ортогональным
матрицам и обладает следующими свойствами:
1. Определитель ортогональной матрицы равен единице.
2. Сумма квадратов элементов, входящих в каждую строку (столбец) равна единице.
3. Если рассматривать каждую строку матрицы как вектор-строку, а каждый столбец – как вектор-столбец, то скалярные произведения двух разных векторов-строк (векторов-столбцов) равны нулю.
Воспользуемся первым свойством ортогональных матриц.
Подставив в (13) вычисленные направляющие косинусы, получим;
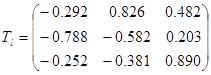 . (23) . (23)
Определитель этой матрицы равен единице:
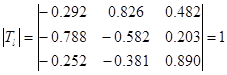 . .
Так как определитель получился равным 1
, то система координат – правая. Поэтому знаки направляющих косинусов остаются без изменения.
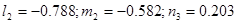 . .
Соответствующие углы будут равны:
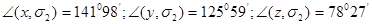 . .
Вычисление максимальных касательных напряжений
В теории упругости доказывается, что максимальные касательные напряжения действуют по двум взаимно перпендикулярным площадкам, расположенным под 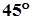 к главным площадкам, по которым действуют главные нормальные напряжения к главным площадкам, по которым действуют главные нормальные напряжения 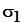 и и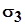 . .
Рис. 1. Максимальные касательные напряжения
Вычисление полного, нормального и касательного напряжений по площадке с заданными направляющими косинусами
Направляющие косинусы нормали 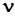 к заданной площадке равны: к заданной площадке равны:
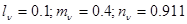
Проекции полного напряжения, действующего на заданной площадке, на координатные оси найдем по формулам:
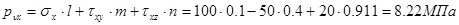 (24) (24)
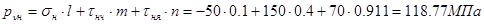

Полное напряжение на этой площадке найдем по формуле:
 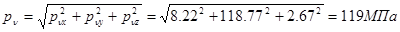 . .
Нормальное напряжение по этой площадке определим, спроектировав координатные составляющие на нормаль к площадке:
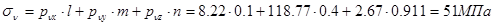 . .
Касательное напряжение на этой площадке найдем по теореме Пифагора (см. рис. 2):
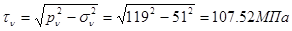 . .
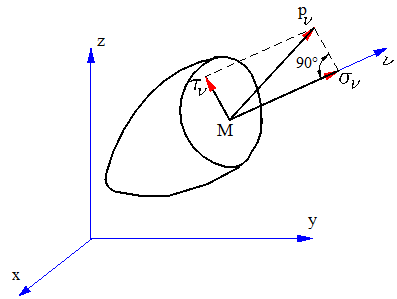
Рис. 2. Полное нормальное и касательное напряжения, действующие по заданной площадке
|