| Міністерство освіти і науки України
Полтавський національний технічний університет
імені Юрія Кондратюка
Факультет будівельний
Кафедра будівельної механіки
РОЗРАХУНКОВО-ГРАФІЧНА
РОБОТА №5
Розрахунок стрижневої системи зі скінченним числом ступенів свободи на вільні та вимушені коливання
402-БП02155
Виконав студент Дрижирук Ю.В.
КерівникШкурупій О.А.
Полтава 2005
Зміст
1. Розрахунок на вільні коливання
1.1 Розрахункова схема та кінематичний аналіз
1.2 Диференційні однорідні рівняння вільних коливань
1.3 Вихідні дані для розрахунку вільних коливань на ЕОМ
1.4 Обчислення частот і головних форм коливань
1.5 Перевірка ортогональності форм коливань
2. Розрахунок на вимушені коливання
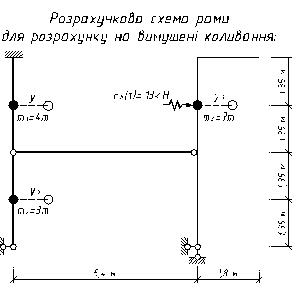
2.1 Розрахункова схема
2.2 Запис рівняння вимушених коливань при частоті 
2.3 Вихідні дані для розрахунку вимушених коливань на ЕОМ
2.4 Обчислення амплітуд сил інерції та амплітуди коливань
2.5 Побудова епюри згинальних моментів від дії динамічних навантажень та її кінематична перевірка
2.6 Динамічні коефіцієнти по зусиллях і по переміщеннях для характерних перерізів системи
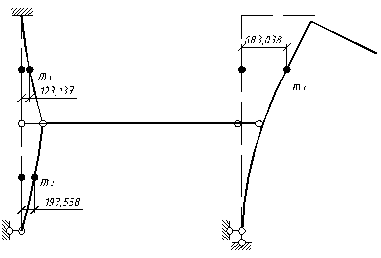
2.7 Деформована схема рами при вимушених коливаннях
Література
Вибір шифру та розрахункової схеми за номером залікової книжки 02155
Перша цифра шифру - це цифра 3 - остання із суми усіх цифр залікової книжки: 0+2+1+5+5=13.
Друга цифра шифру - це цифра 3 - остання із суми усіх цифр залікової книжки без урахування першої: 2+1+5+5=13.
Третя цифра шифру - це цифра 5 - визначається як остання з усіх цифр номера залікової книжки.
Остаточно шифр варіанта - 335.
Номер розрахункової схеми визначається двома останніми цифрами номера залікової книжки, від яких треба відняти 48: 55-30=25. Отже, номер розрахункової схеми - 25.
Вихідні дані:
L=7,2м; h=5,4м; m1
=4т; m2
=3т; m3
=7т; m4
=10т; m5
=8т; n=0,82; Fа
=7кН; Fб
=13кН; Fв
=6кН; Fг
=9кН.
Розрахункова схема.


Виконаємо кінематичний аналіз:
Визначимо кількість ступенів свободи системи:
 , ,
де Д - кількість дисків;
Ш - кількість простих шарнірів;
В0
- кількість опорних в’язей.
Визначимо кількість динамічних ступенів свободи
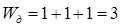
Очевидно, що точкові маси m1,
m2,
m3,
можуть коливатися лише у вертикальному напрямку.
1). Складемо систему диференційних рівнянь вільних коливань, записавши переміщення точкових мас на основі принципу незалежності дії сил:
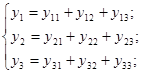 (1) (1)
з урахуванням сил інерції мас:
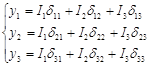 (2) (2)
де І1
- сила інерції маси m1
по вертикалі; І2
- сила інерції маси m2
по вертикалі; І3
- сила інерції маси m3
по вертикалі; δij
- одиничне переміщення по і-тому напрямку викликане дією одиничної сили по j-тому напрямку.
З врахуванням принципу Даламбера:
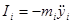
де  - прискорення і-тої маси. - прискорення і-тої маси.
В цьому разі систему (2) можна записати у вигляді:
 (3) (3)
Таким чином ми отримали систему диференційних рівнянь вільних коливань рами.
При складанні цієї системи сили опору середовища не враховані.
2). Вважаємо, що всі точкові маси здійснюють вільні коливання за гармонічним законом із частотою  , тоді розвязок (3) матиме вигляд: , тоді розвязок (3) матиме вигляд:
y1
=A1
.
sin (ωt+φ0
);
y2
=A2
.
sin (ωt+φ0
);
y3
=A3
.
sin (ωt+φ0
).
Продиференціюємо дані вирази двічі, будемо мати:
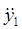 =-A1
.
ω2
sin (ωt+φ0
); =-A1
.
ω2
sin (ωt+φ0
);
 =-A2
.
ω2
sin (ωt+φ0
);
(
4) =-A2
.
ω2
sin (ωt+φ0
);
(
4)
 =-A3
.
ω2
sin (ωt+φ0
). =-A3
.
ω2
sin (ωt+φ0
).
Підставимо (4) в (3) і отримаємо систему диференційних рівнянь вільних коливань системи:
 (5) (5)
Отримана система рівнянь (5) - це система лінійних алгебраїчних рівнянь відносно невідомих амплітуд переміщень точкових мас - А1
, А2
і А3
.
Як відомо, для такої системи можливі два рішення:
а) А1
=А2
=А3
=0, але в цьому випадку коливань немає, тому дане рішення не задовольняє умови задачі;
б) А1
≠0, А2
≠0, А3
≠0. Визначник при невідомих дорівнює 0:
  (6) (6)
частотне рівняння вільних коливань або вікове рівняння,
де  - матриця податливості. - матриця податливості.
3). Для визначення  побудуємо необхідні епюри від одиничних навантажень: побудуємо необхідні епюри від одиничних навантажень:
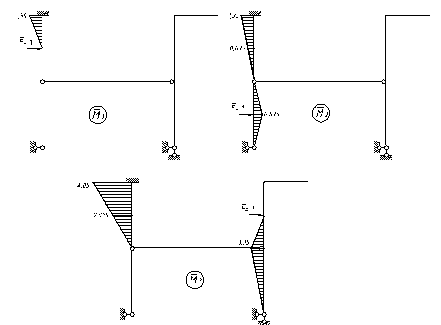
Визначаємо одиничні переміщення:
 . .
 ; ;
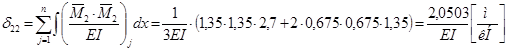 ; ;
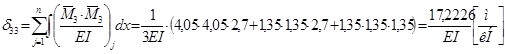 ; ;

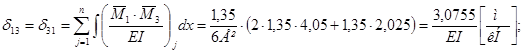
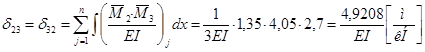 . .
4) Для перевірки правильності обчислення коефіцієнтів матриці податливості, побудуємо сумарну епюру від одиничних навантажень:
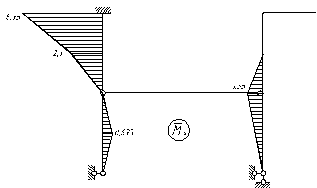
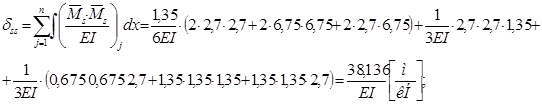

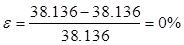
Отже, одиничні переміщення обчислено правильно.
 - матриця податливості; - матриця податливості;
 ; в нашому випадку ; в нашому випадку  . .
1) Використовуючи програму Dinamo16, обчислюємо на ЕОМ спектр частот вільних коливань та форми коливань з точністю 10-5
. В результаті отримаємо:
Спектр частот вільних коливань:
ω1 = 0.08870705
ω2 = 0.69629471
ω3 = 1.08787716
Форми коливань: (приймаємо, що  =1, тоді =1, тоді  ) )
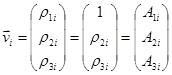 ; ;  ; ;  ; ; 
 ,…, ,…, - амплітуда переміщень 1-ї (n
-ної) маси з і
-тою частотою - амплітуда переміщень 1-ї (n
-ної) маси з і
-тою частотою
2) За отриманими значеннями частот вільних коливань будуємо спектр частот:


3) Зобразимо головні форми коливань, тобто деформовані схеми конструкції, що відповідають певній частоті:
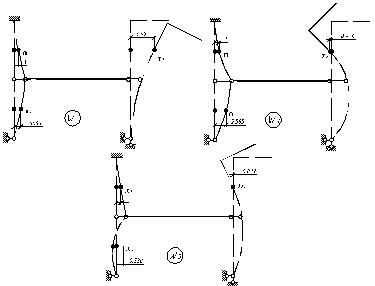
 , ,
де k - номер маси;
i, j - номер форми коливань.
Умова ортогональності І та ІІ форм:
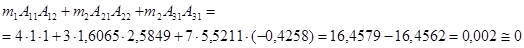
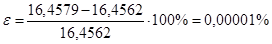 ; ;
Відповідно, умова ортогональності І та ІІІ форм:

Умова ортогональності ІІ та ІІІ форм:

Отже, перевірки для всіх форм коливань виконані й умова ортогональності задовільняється.
n=q/ω1
=0,82;
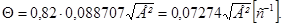
1). Запишемо диференційне рівняння вимушених коливань. Так як сили опору коливанням не враховуються, то переміщення при вимушених коливаннях будуть залежати від сил інерції і збурюючої сили:
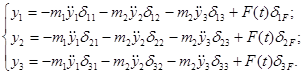
Рішення системи шукаємо для випадку стаціонарних коливань. Вважаємо, що всі маси коливаються за законом збурюючої сили:
уі
=cі
sinθt;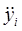 = -cі
θ2
sinθt, = -cі
θ2
sinθt,
сі
- амплітуда переміщень в і-му напрямку.
В цьому разі:
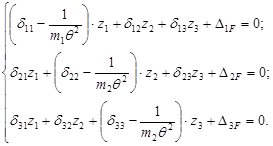
2). Обчислимо вільні члени шляхом побудови епюри згинальних моментів від амплітудного значення збурюючої сили:

Визначимо одиничні переміщення мас під дією зовнішнього навантаження:
 ; ;
 ; ;
 . .
Для перевірки правильності обчислення вільних членів, знайдемо добуток сумарної епюри від одиничного навантаження та епюри моментів від амплітудного значення збурюючої сили:
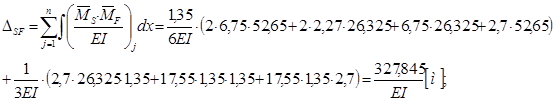

Оскільки  = = , то вільні члени визначено вірно. , то вільні члени визначено вірно.
Співвідношення частот вимушених і вільних коливань:
q/ω1
=0,82; Вектор вільних членів:  . .
Розв’язавши систему рівнянь за допомогою програми Dinamo16, одержимо: амплітуди сил інерції: Z1
= 2,606116 [кН], Z2
= 3.135882 [кН], Z3
= 25.298055 [кН]. Амплітуди коливань: С1
= 123.137351/ЕІ [м],
С2
= 197.557959/ЕІ [м],
С3
= 683.038443/ЕІ [м].
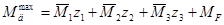 . .
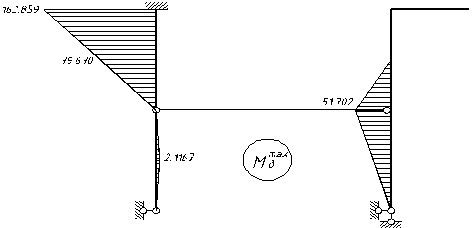
Виконаємо кінематичну перевірку даної епюри. Для цього знайдемо суму амплітуд коливань :
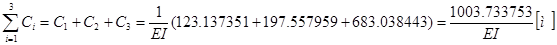 . .
Також знайдемо добуток епюр 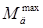 та сумарної епюри від одиничного навантаження: та сумарної епюри від одиничного навантаження:

Оскільки 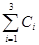 = =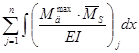 , то епюру моментів від динамічних навантажень побудовано вірно. Відносна похибка обчислень: , то епюру моментів від динамічних навантажень побудовано вірно. Відносна похибка обчислень:
 . .
Динамічний коефіцієнт по зусиллях визначається для характерних перерізів за формулою:
 : :
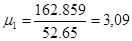 ; ;
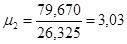 ; ;
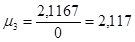 ; ;
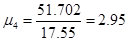 . .
Динамічні коефіцієнти по переміщенням обчислюються за формулою:
 : :
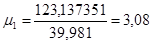 ; ;
 ; ;
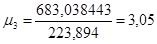 . .
1. Смирнов А.Ф., Александров А.В., Лащеников Б.Я., Шапошников Н.Н. Строительная механика стержневых систем. - М.: Стройиздат, 1981.
2. Дарков А.В., Шапошников Н.Н. Строительная механика. - 8-е изд., перераб. и доп. - М.: Высшая школа, 1986.
3. Киселев В.А. Строительная механика, общий курс - 4-е изд., исправленное и доп. - М.: Стройиздат, 1986.
4. Бутенко Ю.И., Канн С.Н., Пустовойтов В.П. и др. Строительная механика стержневых систем и оболочек. - К.: Вища школа, 1980.
5. Строительная механика. Руководство к практическим занятиям / Под ред. Ю.И. Бутенко. - К.: Вища школа, 1989.
6. Руководство к практическим занятиям по курсу строительной механики (статически определимые и неопределимые системы) / Под ред. Г.К. Клейна. - 3-е изд., перераб. и доп. - М.: Высшая школа, 1973.
7. Методичні вказівки та контрольні завдання з дисципліни „Будівельна механіка (спецкурс)” для студентів денної форми навчання. Частина 3 (стійкість і динаміка будівель і споруд) / Полтава: ПНТУ, 2003. Укладачі: О.А. Шкурупій, Б.П. Митрофанов, А.М. Пащенко.
|