Контрольная работа
Дисциплина:
«Высшая математика»
Тема:
«Универсальная тригонометрическая подстановка»
1. Универсальная тригонометрическая подстановка
Рассмотрим интегрирование выражений полностью зависящих от тригонометрических функций, над которыми выполняются лишь арифметические операции. Такие выражения называются рациональными функциями от тригонометрических функций и в данном случае обозначаются  . Например, . Например,
 , ,  , , 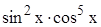 . .
В то же время функция  рациональной не является. рациональной не является.
Теорема
. Интеграл вида  с помощью подстановки с помощью подстановки 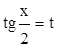 преобразуется в интеграл от рациональной дроби
. преобразуется в интеграл от рациональной дроби
.
Для доказательства выразим  , ,  и и  через через 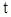 : :
 ; ;
 ; ;
 . .
В результате проведенных преобразований  , ,  и и  превратились в рациональные дроби от превратились в рациональные дроби от 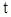 . Подставляя их в исходный интеграл, получаем: . Подставляя их в исходный интеграл, получаем:
 . .
В данном выражении рациональные дроби подставлены в рациональную функцию. Так как над ними выполняются лишь арифметические операции, то в результате получается также рациональная дробь. Итак, рациональную функцию от тригонометрических функций можно проинтегрировать, превратив ее в рациональную дробь.
Подстановка
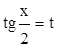 , ,  , , 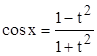 , , 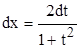
называется универсальной тригонометрической подстановкой.
2. Частные случаи интегрирования выражений, содержащих тригонометрические функции
Рассмотренная в п. 11 универсальная тригонометрическая подстановка позволяет вычислить любой интеграл от функции вида  . Однако на практике она часто приводит к слишком сложным рациональным функциям, интегрирование которых представляет значительную трудность. Есть целый ряд интегралов от тригонометрических функций, которые можно вычислить значительно проще. . Однако на практике она часто приводит к слишком сложным рациональным функциям, интегрирование которых представляет значительную трудность. Есть целый ряд интегралов от тригонометрических функций, которые можно вычислить значительно проще.
1. Интегралы типа  удобно вычислять с помощью подстановки удобно вычислять с помощью подстановки 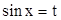 . Тогда . Тогда  и получаем простой интеграл и получаем простой интеграл 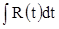 . .
2. Интегралы типа 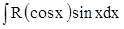 удобно вычислять с помощью подстановки удобно вычислять с помощью подстановки  . Тогда . Тогда  и интеграл приводится к виду и интеграл приводится к виду  . .
3. Если подынтегральная функция зависит только от  ( (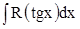 ), то удобна замена ), то удобна замена  . В этом случае . В этом случае  и и  . В результате получаем . В результате получаем  . .
4. Если подынтегральная функция является рациональной относительно четных степеней  и и  , то есть , то есть  , то в этом случае также удобна замена , то в этом случае также удобна замена  . При этом: . При этом:
 ; ;
 ; ;
 . .
Данная подстановка в этом случае дает более простую рациональную дробь, чем с использованием универсальной тригонометрической подстановки.
Пусть дан интеграл 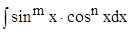 , где , где  и при этом хотя бы одно из этих чисел нечетное. Допустим, что и при этом хотя бы одно из этих чисел нечетное. Допустим, что  . Тогда . Тогда
 . .
Далее делается замена 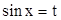 , и получаем , и получаем  . .
6. Пусть дан интеграл 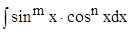 , где , где 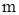 и и  неотрицательные и четные. Положим, что неотрицательные и четные. Положим, что  , ,  . Тогда . Тогда
 ; ;  . .
Данная замена позволяет в два раза понизить степень тригонометрических функций. Раскрывая скобки в интеграле  , получаем снова случаи 5 или 6. , получаем снова случаи 5 или 6.
7. Пусть дан 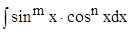 , где , где 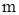 и и  – четные и хотя бы одно из этих чисел отрицательно. Тогда удобна та же замена, что и в случае 4. – четные и хотя бы одно из этих чисел отрицательно. Тогда удобна та же замена, что и в случае 4.
8. В случае 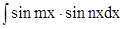 используется тригонометрическая формула используется тригонометрическая формула
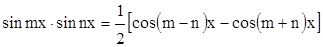
и интеграл превращается в два табличных интеграла.
9. В случае 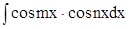 используется тригонометрическая формула используется тригонометрическая формула
 . .
10. В случае 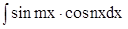 используется тригонометрическая формула используется тригонометрическая формула
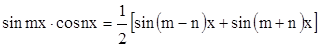 . .
3. Тригонометрические подстановки для интегралов вида
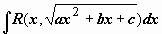
Рассмотрим тригонометрические подстановки для вычисления таких интегралов, которые сводят подынтегральную функцию к функции, рационально зависящей от 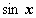 и и 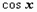 . Вначале выполняется выделение полного квадрата в трёхчлене (и соответствующей линейной замены переменной), в результате этого интеграл сводится, в зависимости от знаков . Вначале выполняется выделение полного квадрата в трёхчлене (и соответствующей линейной замены переменной), в результате этого интеграл сводится, в зависимости от знаков  и дискриминанта трёхчлена, к интегралу одного из следующих трёх видов: и дискриминанта трёхчлена, к интегралу одного из следующих трёх видов:
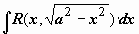 , , 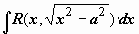 , , 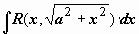 . .
Следующий шаг:
1) 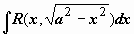 рационализируется подстановкой x
= a
sin t
(или x
= a
cos t
). Замена переменной в неопределённом интеграле. рационализируется подстановкой x
= a
sin t
(или x
= a
cos t
). Замена переменной в неопределённом интеграле.
2) 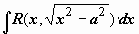 рационализируется подстановкой рационализируется подстановкой 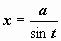 (или (или 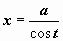 , или , или 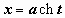 ). ).
3) 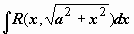 рационализируется подстановкой x
= a
tg t
(или x
= a
ctg t
, или x
= a
sh t
). рационализируется подстановкой x
= a
tg t
(или x
= a
ctg t
, или x
= a
sh t
).
 Пример 1. Пример 1.  . Интеграл вида . Интеграл вида 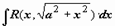 , из возможных подстановок наиболее удобной оказывается x
= ctg t
. , из возможных подстановок наиболее удобной оказывается x
= ctg t
.
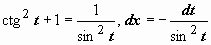 , ,
поэтому 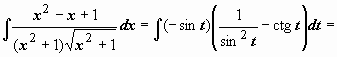
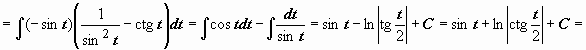
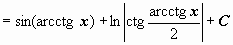
или
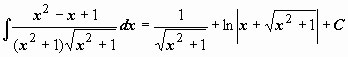 . .
 Пример 2. Пример 2.
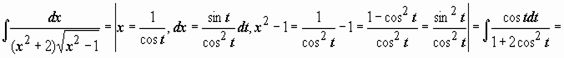
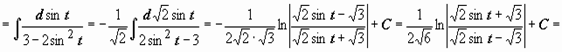
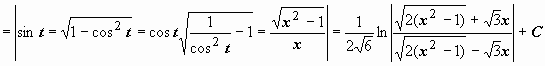
3. Интегрирование некоторых алгебраических иррациональностей
Рассмотрим теперь интегрирование функций, содержащих радикалы. Не от всякой иррациональной функции интеграл выражается через элементарные функции. Однако в наиболее простых случаях, когда над радикалами выполняются рациональные действия, это удается сделать. Необходимо отметить, что все такие иррациональные функции интегрируются посредством их рационализации, то есть избавления от корней.
1. Пусть дан интеграл
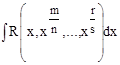 , ,
где 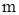 , ,  ,…, ,…, 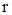 , ,  . Найдем общий знаменатель дробей . Найдем общий знаменатель дробей  ,…, ,…,  . Пусть это число . Пусть это число  . Сделаем подстановку . Сделаем подстановку  , , 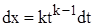 . В этом случае все дробные степени становятся целыми и подынтегральная функция становится рациональной относительно . В этом случае все дробные степени становятся целыми и подынтегральная функция становится рациональной относительно 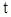 . .
2. Рассмотрим общий случай подобных интегралов:
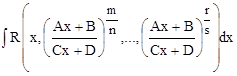 , ,
где 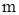 , ,  ,…, ,…, 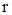 , ,  . .
Чтобы получить рациональную функцию, находят общий знаменатель дробей  ,…, ,…,  (обозначим его (обозначим его  ) и делают замену переменной ) и делают замену переменной  . В этом случае . В этом случае

 . .
Очевидно, если 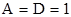 и и 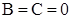 , то случай 2 переходит в случай 1. Кроме того, необходимо иметь в виду, что в обоих случаях основания всех степеней должны быть одинаковы: в первом случае , то случай 2 переходит в случай 1. Кроме того, необходимо иметь в виду, что в обоих случаях основания всех степеней должны быть одинаковы: в первом случае 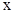 , во втором – , во втором –  . .
4. Интегрирование некоторых иррациональных функций с помощью тригонометрических подстановок
Рассмотри снова интегралы, содержащие квадратный трехчлен:
 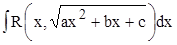 . .
Выделив полный квадрат под корнем, получим один из трех интегралов:  , , 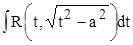 , , 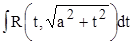 . Все они вычисляются с помощью тригонометрических подстановок. . Все они вычисляются с помощью тригонометрических подстановок.
1. 
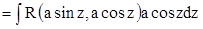 . .
2. 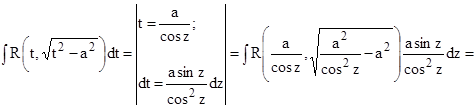
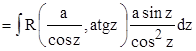 . .
3. 
 . .
Во всех трех случаях после проведенных подстановок интегралы пришли к виду, рассмотренному в п. 2.
5. Интегралы, не выражающиеся через элементарные функции
В п. 1 была сформулирована теорема о том, что любая непрерывная функция имеет первообразную. Однако необходимо иметь в виду, что не всегда первообразная выражается в конечном виде через элементарные функции.
К таким интегралам следует отнести
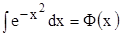 , ,  , ,  , ,  , ,
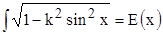 ( (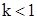 ). ).
Во всех подобных случаях первообразная представляет собой некоторую новую функцию, которая не сводится к комбинации конечного числа элементарных функций.
Например, та из первообразных 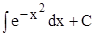 , которая обращается в нуль при , которая обращается в нуль при 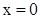 , называется функцией Гаусса и обозначается , называется функцией Гаусса и обозначается  . Эта функция хорошо изучена, составлены подробные таблицы ее значений. То же самое можно сказать и о других подобных функциях. . Эта функция хорошо изучена, составлены подробные таблицы ее значений. То же самое можно сказать и о других подобных функциях.
Литература
1. Александров В.В., Потапов М.К., Пасиченко П.И., Потапов М.К. Александров В.В., Потапов М.К и др. Алгебра, тригонометрия и элементарные функции. Учебник. М: Высшая школа, 2001. – 736 с.
2. Крищенко Александр, Канатников Анатолий Аналитическая геометрия: Учебное пособие для студентов высших учебных заведений. Изд-во «Академия», 2009. – 208c.
3. Макарычев Юрий Тригонометрия. Издательство: ПРОСВЕЩЕНИЕ, 2004. – 360 с.
4. Потапов Михаил Задачи по алгебре, тригонометрии и элементарными функциями. Издательство: ЭКЗАМЕН XXI, 2008. – 160 с.
5. Тоом А., Гельфанд И., Львовский С. Тригонометрия. МЦМНО, 2003. – 200 с.
6. Шахмейстер А.Х. ТРИГОНОМЕТРИЯ 1-е изд. МГУ, 2006. – 672 с.
|