Великая теорема Ферма – два коротких доказательства
Бобров А.В.
123098, г. Москва, ул. Маршала Новикова, д.10, корп. 1, кв. 15
Контактный телефон – 193-42-34
Последняя теорема Ферма, иногда называемая Великой, формулируется следующим образом:
В равенстве 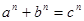 числа числа 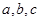 и и  не могут быть одновременно целыми положительными, если не могут быть одновременно целыми положительными, если 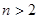 . .
Предположим, такие числа существуют. Тогда должны выполняться следующие условия:
· Равенство справедливо для взаимно простых, не имеющих общих целых множителей, кроме 1, чисел 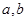 и и 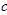 , т.е. два числа – всегда нечетные. , т.е. два числа – всегда нечетные.
· Существуют числа 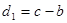 и и 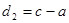 , или , или 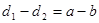 , то есть для произвольно выбранных натуральных , то есть для произвольно выбранных натуральных  существует бесконечное множество рациональных, действительных или комплексных чисел существует бесконечное множество рациональных, действительных или комплексных чисел 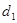 и и 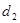 , удовлетворяющих приведенному равенству, если в этом множестве выполнимы арифметические действия. Для целых , удовлетворяющих приведенному равенству, если в этом множестве выполнимы арифметические действия. Для целых 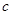 числа числа 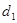 и и 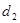 также будут целыми. также будут целыми.
Вариант№1
Равенство 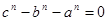 (1) (1)
путем последовательного деления на числа 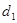 и и 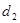 всегда преобразуется в два многочлена (уравнения) всегда преобразуется в два многочлена (уравнения)  -ой степени относительно -ой степени относительно 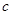 : :
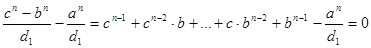 (2) (2)
 (3) (3)
Равенства (2) и (3) получены путем тождественных преобразований равенства (1), т.е. должны выполняться при одних и тех же значениях целых положительных чисел 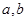 и и 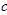 . По определению, необходимым и достаточным условием тождественности двух многочленов над некоторым числовым полем (в нашем случае – над множеством целых чисел) является равенство коэффициентов членов, содержащих одни и те же аргументы в одинаковых степенях, то есть должно выполняться: . По определению, необходимым и достаточным условием тождественности двух многочленов над некоторым числовым полем (в нашем случае – над множеством целых чисел) является равенство коэффициентов членов, содержащих одни и те же аргументы в одинаковых степенях, то есть должно выполняться:
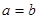 , , 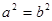 , … , … 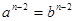 , , 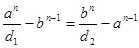 (4) (4)
Из (1) и (4) следует 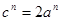 , , 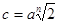 то есть число то есть число 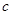 , как общий арифметический корень уравнений (1), (2) и (3) не может быть рациональным при целых , как общий арифметический корень уравнений (1), (2) и (3) не может быть рациональным при целых 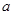 , , 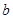 , , 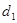 и и 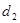 . .
Из равенства свободных членов следует:
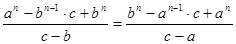 ,или ,или ,или ,или
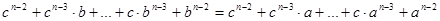 (5) (5)
Вычитая из правой части равенства (5) левую, получим:
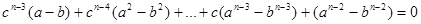 (6) (6)
или, если 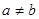 , сократив на , сократив на 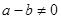 , получим: , получим:
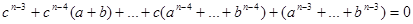 (7) (7)
Из равенства (7) следует, что для 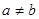 числа числа 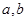 и и 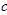 не могут быть одновременно положительными. не могут быть одновременно положительными.
Представленные преобразования позволяют сделать следующие выводы:
· для тождественных над множеством рациональных чисел многочленов (2) и (3) при 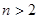 число число 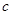 , как общий арифметический корень уравнений (1), (2) и (3), не может быть рациональным при целых положительных , как общий арифметический корень уравнений (1), (2) и (3), не может быть рациональным при целых положительных 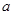 , , 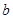 , , 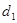 и и 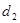 ; ;
· многочлены (2) и (3) для 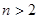 и натуральных и натуральных 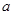 и и 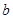 не тождественны над множеством рациональных чисел, если делители не тождественны над множеством рациональных чисел, если делители 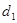 и и 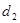 равенства (1) являются иррациональными, откуда следует иррациональность числа равенства (1) являются иррациональными, откуда следует иррациональность числа 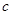 ; ;
· числа 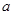 , , 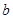 и и 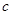 в равенстве (1) для в равенстве (1) для 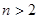 не могут быть одновременно рациональными. не могут быть одновременно рациональными.
Для 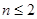 противоречие исчезает, коэффициенты при противоречие исчезает, коэффициенты при 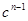 равны 1, а равенство свободных членов после подстановки значений равны 1, а равенство свободных членов после подстановки значений 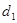 и и 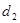 обращается в тождество: обращается в тождество:
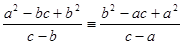 . (8) . (8)
Если правую и левую части равенства (5) обозначить соответственно через 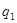 и и  , где , где 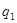 и и  - целые положительные числа, то многочлены (2) и (3) преобразуются в квадратные уравнения относительно - целые положительные числа, то многочлены (2) и (3) преобразуются в квадратные уравнения относительно 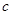 : :
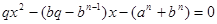
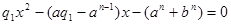 (9), (9),
где неизвестное 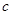 обозначено общепринятым образом через обозначено общепринятым образом через 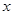 , то есть , то есть 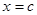 . .
Из условий эквивалентности или анализа причин неэквивалентности этих уравнений следуют те же выводы.
Это доказательство опубликовано в 1993 г. в журнале РАН «Вопросы истории естествознания и техники», №3.
Со стороны оппонентов не поступило никаких возражений по существу, кроме утверждения, что в используемых для доказательства уравнениях известные и неизвестные величины зависят друг от друга – как будто может быть иначе. Любое аналитическое выражение, в котором присутствуют известные и неизвестные величины, есть выражение зависимости между ними, поэтому я не могу согласиться с подобным опровержением.
Вариант№2
Пусть в равенстве 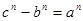 числа числа 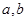 и и 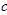 - взаимно простые, - взаимно простые, 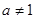 - нечетное. Для любых положительных чисел выполнима операция нахождения арифметического значения квадратного корня, то есть можно записать: - нечетное. Для любых положительных чисел выполнима операция нахождения арифметического значения квадратного корня, то есть можно записать:
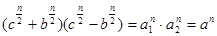 (1) (1)
где  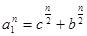 , , 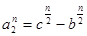 - действительные положительные множители числа - действительные положительные множители числа 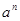 . .
Из (1) следует:
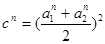 , , 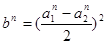 (2) (2)
В соответствии со свойствами показательной функции, для действительных положительных чисел 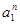 , , 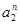 и целого и целого 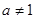 существуют единственные значения показателей степени существуют единственные значения показателей степени 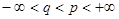 , удовлетворяющие равенствам: , удовлетворяющие равенствам:
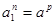 , ,  (3) (3)
где  , , 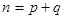 . .
Из (3) следует  , ,  , или после сокращения на числа , или после сокращения на числа 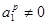 , , 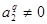 получим: получим:
 (4) (4)
Из (1), (2) и (3) следует:
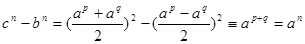 , (5) , (5)
или, с учетом равенств (3) и (4):
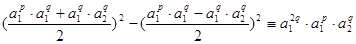 (6) (6)
Вынесем за скобки общий множитель 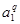 : :
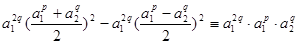 (7) (7)
Из (5) и (7) следует, что числа 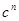 , ,  и и 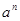 содержат общий множитель содержат общий множитель 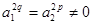 , что противоречит условию их взаимной простоты, если , что противоречит условию их взаимной простоты, если 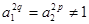 . Из . Из  следует следует  , ,  , то есть , то есть 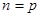 , , 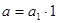 , и равенства (5) и (7) принимают вид: , и равенства (5) и (7) принимают вид:
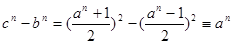 (8) (8)
Из (8) следует, что при нечетном 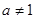 числа числа 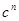 и и  также целые, причем всегда имеет место тождество: также целые, причем всегда имеет место тождество:
 (9) (9)
что для одновременно целых 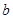 , , 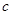 и и  выполнимо только при выполнимо только при 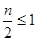 , или , или 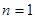 , , 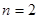 , что и требовалось доказать. , что и требовалось доказать.
Доказательство можно вести и несколько иным способом. Все числа равенства 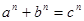 , где , где 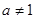 , , 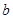 и и  - произвольно выбранные натуральные числа, - произвольно выбранные натуральные числа, 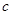 - действительное положительное число, через преобразования (1)…(4) могут быть выражены в виде слагаемых тождества (5). - действительное положительное число, через преобразования (1)…(4) могут быть выражены в виде слагаемых тождества (5).
Вынесем за скобки множитель  и поделим на него все слагаемые тождества (5): и поделим на него все слагаемые тождества (5):
 (10) (10)
где 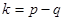 . .
В соответствии со свойствами показательной функции, произвольно выбранным натуральным числам 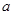 , , 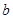 и и  , например из равенства (5), соответствует единственное значение , например из равенства (5), соответствует единственное значение 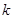 , удовлетворяющее условию: , удовлетворяющее условию:
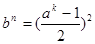 (11) (11)
тогда  , или , или
 (12) (12)
где 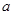 , , 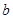 и и  - целые числа. - целые числа.
Из (10), (11) и (12) следует:
 (13) (13)
то есть числа 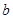 и и 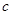 могут быть одновременно целыми только при могут быть одновременно целыми только при 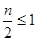 , или , или 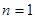 , , 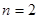 . При . При 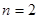 числа числа 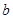 и и 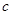 есть последовательные целые числа. Еще Эвклидом доказано, что всякое нечетное число может быть выражено, как разность квадратов двух последовательных целых чисел, которые и могут быть найдены с помощью тождества (10) для любых целых есть последовательные целые числа. Еще Эвклидом доказано, что всякое нечетное число может быть выражено, как разность квадратов двух последовательных целых чисел, которые и могут быть найдены с помощью тождества (10) для любых целых 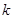 и нечетных и нечетных 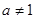 . .
Отметим, что равенство (12) получено путем деления равенства (5) на множитель  , при этом число , при этом число  в этих равенствах одно и то же, откуда следует в этих равенствах одно и то же, откуда следует 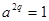 , ,  , , 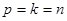 , и тождество (10) принимает вид тождества (8). , и тождество (10) принимает вид тождества (8).
Отметим также, что тождества (8) и (10) справедливы не только для целых значений 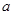 . Подставляя вместо . Подставляя вместо 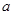 любую рациональную дробь и полагая любую рациональную дробь и полагая 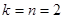 , можно найти все Пифагоровы числа. , можно найти все Пифагоровы числа.
Приведенные преобразования равенства Ферма над множеством натуральных чисел показывают, что с помощью конечного числа арифметических действий оно всегда приводится к тождеству (13), что и доказывает теорему.
Я счел необходимым в дополнение к размещенному на сайте доказательству предложить и эти два варианта, один из которых в сравнении с ранее размещенным является более развернутым.
А.В.Бобров
Великая теорема Ферма
Бобров Александр Владимирович, 1936 г. р., образование высшее, закончил в 1960 году МВТУ им. Баумана по специальности инженер-механик. В настоящее время – пенсионер.
Домашний адрес: 123098, г. Москва, ул. Маршала Новикова, д. 10, корп.1, кв. 15.
Телефон (495) 193-42-34, моб. тел. 8-903-560-07-15
The evidence of the Fermat theorem
Alexander V. Bobrov
The evidence of the Fermat great theorem by elementary method is presented
|