| Исходные данные к курсовому проекту
Рассматривается последний этап посадки космического аппарата (КА) на планету. При построении математической модели предположим:
1) посадка осуществляется по нормали к поверхности планеты, планета неподвижна и в районе посадки плоская;
2) на КА действуют сила тяжести G=mg, причем g=const и сила тяги 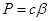 , где с=const, а β – секундный расход массы m, , где с=const, а β – секундный расход массы m, 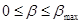 ; ;
3) аэродинамические силы отсутствуют.
Уравнения движения КА могут быть представлены в виде:
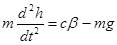 ; ; 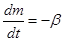 ; ; 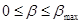 , где h – текущая высота; , где h – текущая высота;
или в нормальной форме:
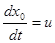 ; ; 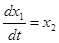 ; ; 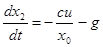 ; ; 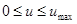 . .
Здесь введены обозначения:
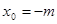 ; ; 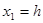 ; ; 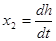 ; ; 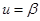 ; ; 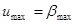 . .
Граничные условия имеют вид:
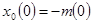 ; ; 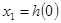 ; ; 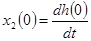 ; ; 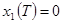 ; ; 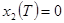 , ,
причем Т заранее неизвестно. Требуется найти программу управления u*(t), обеспечивающую мягкую посадку при минимальном расходе топлива, то есть 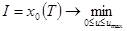 . .
Исходные данные для расчетов
| Начальная масса КА
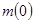 , кг. , кг.
|
Начальная высота
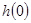 , км. , км.
|
Начальная
скорость
 , км/с , км/с
|
Отношение силы тяги
к начальной массе 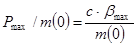 , м/с2 , м/с2
|
| 500
|
190
|
2,65
|
42,5
|
| 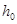 =190000 м. =190000 м.
|
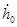 =2650 м/с =2650 м/с
|
Ускорение силы тяжести для планеты g=1,62 м/с2
, величина с=3000 м/с.
Задание к курсовому проекту
1.) Составить гамильтониан Н, воспользовавшись необходимыми условиями оптимальности для задачи Майера.
2.) Из условия максимизации Н по u найти оптимальное управление.
3.) Получить каноническую систему уравнений и в результате прийти к краевой задаче, для которой в момент t=0 заданы компоненты x0
, x1
, x2
, а в момент t=T‑компоненты x1
, x2
, ψ0
.
4.) Из условия Н(Т)=0 получить соотношение для определения неизвестного времени Т.
5.) Произвести анализ необходимых условий оптимальности, начав с исследования возможности существования особого вырожденного управления, то есть случая, когда функция переключения
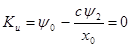 . .
Доказать, что Кu
не может обратиться в нуль на конечном интервале времени и, следовательно, особого управления в данной задаче не существует.
Показать, что Кu
есть монотонная функция t.
Рассмотреть четыре возможных случая:
а) Ku
>0 для всех 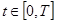 ; ;
б) Ku
<0 для всех 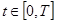 ; ;
в) Ku
>0 для 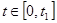 , Ku
<0 для , Ku
<0 для 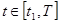 ; ;
г) Ku
<0 для 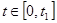 , Ku
>0 для , Ku
>0 для 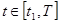 . .
Показать, в каких случаях (из физических соображений) мягкая посадка невозможна, в каком из реализуемых случаев расход топлива меньше.
Получить программу оптимального управления, когда до некоторого момента t1
управление отсутствует u*=0, а начиная с t=t1
, управление равно своему максимальному значению u*=umax
, что соответствует минимальному расходу топлива.
6.) Решить каноническую систему уравнений, рассматривая ее для случаев, когда 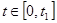 и управление u*=0, и когда и управление u*=0, и когда 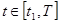 , u*=umax
. , u*=umax
.
Приравнивая х1
(Т) и х2
(Т) нулю, получить два уравнения относительно t1
и Т. Таким образом, краевую задачу свести к системе, состоящей из двух нелинейных уравнений относительно двух неизвестных t1
, Т. Составить программу расчета. Получив решение этой системы, решить полностью исходную задачу программирования оптимального управления мягкой посадкой КА на планету. В заключение следует построить фазовую траекторию спуска КА и определить конечную массу m(Т).
Выполнение задания курсового проекта
Нам известно, что
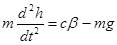 , где с – сила тяги двигателя, , где с – сила тяги двигателя,
m – масса космического аппарата;
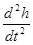 – ускорение аппарата. – ускорение аппарата.
То есть, масса · ускорение = сумме сил, действующих на аппарат.
β – секундный расход массы m: 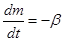 . .
Расход массы обеспечивает силу тяги двигателя (P=c·β), ее можно менять в пределах 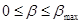 . .
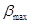 можно найти из исходных данных – выразив из отношения силы тяги к начальной массе Pmax
/m(0): можно найти из исходных данных – выразив из отношения силы тяги к начальной массе Pmax
/m(0):
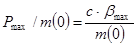 ; ;
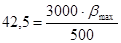 ; ;
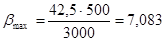 кг/с. кг/с.
Наш критерий оптимизации 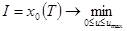 . Введем принятые в исходных данных обозначения: . Введем принятые в исходных данных обозначения:
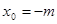 ; ; 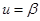 . .
Начальный момент времени t=0, конечный момент времени – момент посадки КА (момент столкновения с планетой) t=T.
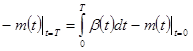 ; ;
Тогда критерий оптимизации:
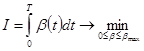 ; ;
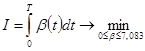 . (Здесь . (Здесь 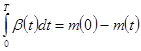 .) .)
Теперь необходимо написать уравнение состояния системы. Для этого нужно ввести переменные состояния и входную переменную.
Порядок дифференциального уравнения n=3, отсюда 3 уравнения состояния:
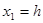 ; ;
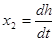 ; ;
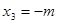 . .
Выберем управление:
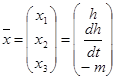 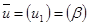 ; ;
Подставляем уравнения состояния, получим:
так как 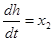 и и 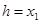 , отсюда , отсюда
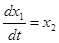 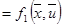 ; ;
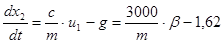 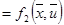 ; ;
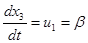 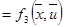 . .
Критерий оптимизации:
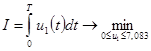 . .
Введем переменные х0
и хn+1
(то есть х4
).
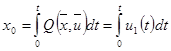 , где t – текущее время. , где t – текущее время.
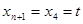 . .
Тогда основные уравнения состояния:
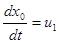 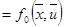
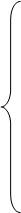 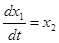 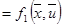
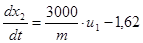 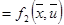
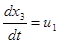 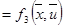
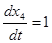 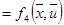
Составим гамильтониан Н:
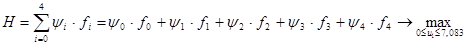 ; ;
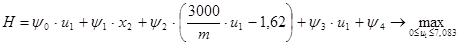 . .
Оптимальному управлению соответствует максимум функции Гамильтона в заданной области возможных управлений. Причем этот максимум равен нулю.
То есть нужно добиться максимума этой функции, меняя u1
. Это и будет оптимальное управление.
Для функций ψi
тоже получим сопряженные уравнения, которые имеют вид 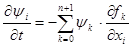 : :
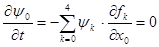 – так как функция не зависит от х0
, – так как функция не зависит от х0
,
следовательно производная равна нулю;
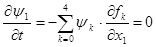 – аналогично, так как функция не зависит от х1
. – аналогично, так как функция не зависит от х1
.
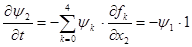
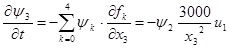
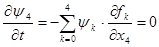
Итак, нужно найти максимум гамильтониана:
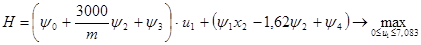
Функция переключения:
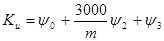
Используя для вычислений Mathcad, получим оптимальное управление:
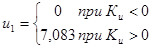
Таким образом оказалось, что оптимальное управление должно осуществляться на предельных ресурсах. То есть либо двигатель должен быть совсем выключен (при Ku
<0), либо включен на максимальную мощность (при Ku
>0).
Посмотрим, как меняется функция переключения Кu
во времени:
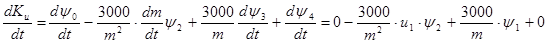 ; ;
Для определения ψ1
и ψ2
решаем сопряженные уравнения:
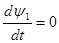 , следовательно, ψ1
= const, обозначим ψ1
=с1
. , следовательно, ψ1
= const, обозначим ψ1
=с1
.
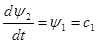 , следовательно, , следовательно, 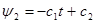 , где c2
= const. , где c2
= const.
Итак,
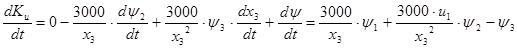
Масса КА всегда положительна, а с=3000 = const – величина постоянная, поэтому производная 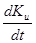 имеет всегда постоянный (один и тот же) знак. То есть величина Ku
либо всё время монотонно возрастает, либо всё время монотонно убывает. А это означает, что она может пройти через ноль только один раз. имеет всегда постоянный (один и тот же) знак. То есть величина Ku
либо всё время монотонно возрастает, либо всё время монотонно убывает. А это означает, что она может пройти через ноль только один раз.
Рассмотрим четыре возможных случая:
а)
Ku
>0 для всех 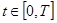 ; ;
б)
Ku
<0 для всех 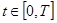 ; ;
в)
Ku
>0 для 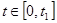 , Ku
<0 для , Ku
<0 для 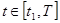 ; ;
г)
Ku
<0 для 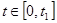 , Ku
>0 для , Ku
>0 для 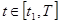 . .
В случаях б)
(когда двигатель КА выключен на всем протяжении посадки) и в)
(когда двигатель включен на максимальную мощность до какого-то момента времени t=t*, а затем полет происходит с выключенным двигателем до самой посадки) – говорить о мягкой посадке не приходится. Эти варианты означают падение КА на планету. Поэтому оптимальными (и вообще допустимыми) их считать нельзя.
Следовательно, остаются два реализуемых варианта – а)
и г)
. И оптимальное управление предполагает либо всё время включенный на максимальную мощность двигатель, либо полет с выключенным двигателем до какого-то момента t=t*, а затем полет с двигателем, включенным на максимальную мощность до момента посадки. Естественно, что во втором случае (г) расход топлива меньше, так как часть пути проделывается с выключенным двигателем.
Поэтому оптимальным управлением в данной ситуации можно считать полет с выключенным двигателем, затем происходит включение двигателя и полет продолжается с двигателем, включенным на максимальную мощность.
Итак, оптимальному управлению соответствует
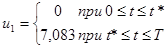
На первом участке полета, на котором u1
=0:
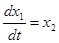
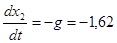
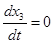
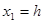 ; ; 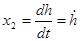 ; ; 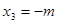 ; ;
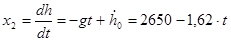 ; ;
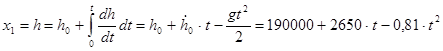 ; ;
 . .
Рассмотрим второй участок полета u1
=7,083:
Зададимся условием, что при t=t* (в момент включения двигателя):
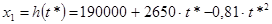 ; ;
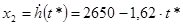 ; ;
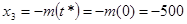 . .
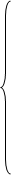 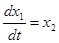
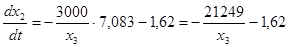
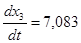
На отрезке полета со включенным двигателем:
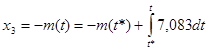 ; ;
так как 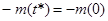 , запишем: , запишем:
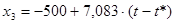 . .
Теперь, зная х3
, можно выразить х2
:
 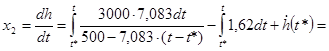 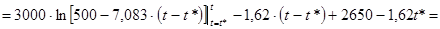
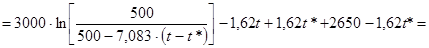
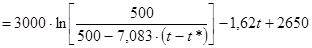 . .
Теперь, зная х2
выразим х1
:
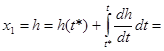
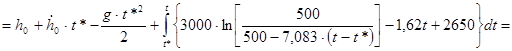

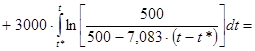
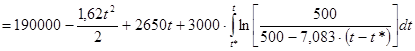 ; ;
На отрезке пути h(t):
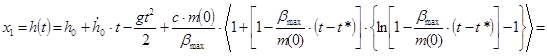
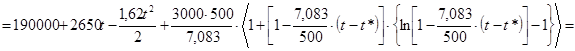
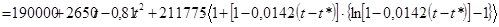
В момент посадки t=T высота и скорость должны быть равны нулю, то есть 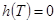 и и 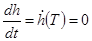 . На основании этого утверждения приравняем х1
(T) и х2
(Т) нулю и получим таким образом два уравнения относительно t* и T. Таким образом, краевая задача у нас свелась к системе, состоящей из двух нелинейных уравнений относительно двух неизвестных t* и Т: . На основании этого утверждения приравняем х1
(T) и х2
(Т) нулю и получим таким образом два уравнения относительно t* и T. Таким образом, краевая задача у нас свелась к системе, состоящей из двух нелинейных уравнений относительно двух неизвестных t* и Т:
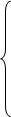 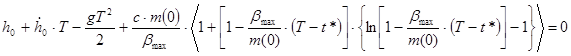

Из второго уравнения системы выразим момент времени, на котором включается двигатель:
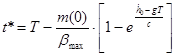 ; ;
Подставим это выражение в первое уравнение системы, получим уравнение для нахождения времени полета T (оно же время посадки):
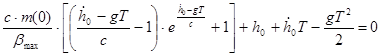
Для расчета времени полета Т воспользуемся программой Mathcad. На следующем листе приведены эти вычисления[1]
:
Теперь, зная Т и t*, можно определить конечную массу космического аппарата m(T):
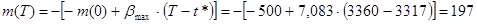 кг. кг.
Можно рассчитать высоту h (t*), на которой КА должен включить двигатели:
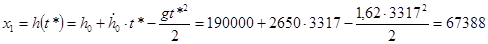 м. м.
Таким образом, включение двигателей происходит на 3317-ой секунде полета на высоте около 67 км. от поверхности планеты. Тот же результат мы наблюдаем и на графике.
[1]
Все дальнейшие вычисления также производились в программе Mathcad
|