Содержание.
Введение……………………………………………………………………….2
Глава
I
. Нормированные пространства…………………………………..3
§1. Понятие нормированного пространства........................................3
§2. Пространства суммируемых функций…………………………...5
§3. Интеграл Лебега – Стилтьеса………………………………..........7
Глава
II
. Интерполяция в пространствах суммируемых функций….11
§1. Теорема Марцинкевича и ее применение……………………...11
§2.Теорема Рисса–Торина и ее применение ………………………15
Глава
III
. Пространства суммируемых последовательностей…..…....24
§1. Основные понятия……………………………………………….24
§2. Связь между коэффициентами Фурье  -периодической функции и ее нормой в -периодической функции и ее нормой в 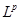 …………….……………………………25 …………….……………………………25
Литература………………………………………………………………...28
Введение.
Понятие нормированного пространства – одно из самых основных понятий функционального анализа. Теория нормированных пространств была построена, главным образом, С.Банахом в 20-х годах 20 века. В работе эта теория прилагается к изучению суммируемых функций и последовательностей с позиций функционального анализа. Эти функции и последовательности образуют нормированные пространства, на которых вводятся операции сложения и умножения на число, а также норма.
Основным объектом классического функционального анализа являются операторы, действующие из одного банахова пространства в другое.
Целью данной работы является рассмотрение линейных операторов, действующих из одного пространства суммируемых функций в другое, а также в пространство суммируемых последовательностей.
Основные понятия нормированных пространств изложены в первой главе.
Вторая глава посвящена интерполяции в пространствах измеримых функций. Рассмотрена теорема Марцинкевича, являющаяся одной из классических в теории интерполяции, и дано ее подробное доказательство. Приводится доказательство непрерывности оператора свертки с использованием данной теоремы. Также рассмотрена интерполяционная теорема Рисса – Торина и ее применение.
В третьей главе даны основные понятия пространства суммируемых последовательностей, доказана связь между коэффициентами Фурье  - периодической функции и ее нормой в - периодической функции и ее нормой в 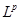 при помощи теоремы Марцинкевича. при помощи теоремы Марцинкевича.
Глава
I
. Нормированные пространства.
§1. Понятие нормированного пространства.
Введем основные понятия теории нормированных пространств.
Определение.
Непустое множество 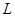 называется линейным пространством
, если оно удовлетворяет следующим условиям: называется линейным пространством
, если оно удовлетворяет следующим условиям:
Ι. Для любых двух элементов 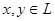 однозначно определен элемент однозначно определен элемент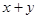 , называемый их суммой, причем , называемый их суммой, причем
1. 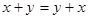 (коммутативность) (коммутативность)
2. 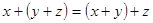 (ассоциативность) (ассоциативность)
3. В 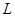 существует такой элемент 0, что существует такой элемент 0, что  для всех для всех 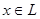
4. Для каждого 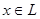 существует такой элемент существует такой элемент 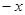 , что , что 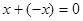 . .
II. Для любого числа 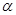 и любого элемента и любого элемента 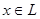 определен элемент определен элемент  , причем , причем
5. 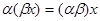
6. 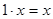
III. Операции сложения и умножения связаны между собой дистрибутивными законами:
7. 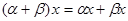
8. 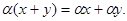
Определение.
Линейное пространство 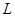 называется нормированным,
если на нем задана неотрицательная функция называется нормированным,
если на нем задана неотрицательная функция 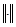 , называемая нормой, удовлетворяющая условиям: , называемая нормой, удовлетворяющая условиям:
1. 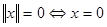 ; ;
2. 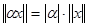 для любого для любого 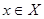 и любого числа и любого числа 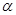 ; ;
3. 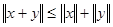 для любых для любых 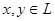 (неравенство треугольника). (неравенство треугольника).
Определение.
Оператором
называется отображение 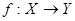 , где , где 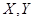 - это линейные пространства. - это линейные пространства.
Определение.
Оператор 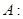 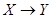 называется линейным
, если для любых элементов называется линейным
, если для любых элементов 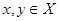 и любых чисел и любых чисел  R
выполняется равенство: R
выполняется равенство:
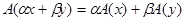 . .
Определение.
Пусть 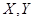 - линейные нормированные пространства, - линейные нормированные пространства,
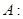 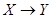 – линейный оператор, – линейный оператор,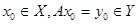 . .
Линейный оператор непрерывен в точке  , если из того, что
, если из того, что 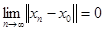 следует, что следует, что 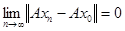 . .
Определение.
Линейный оператор 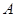 непрерывен
,
если он непрерывенв каждой точке непрерывен
,
если он непрерывенв каждой точке 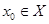 . .
Определение.
Линейный оператор называется ограниченным
, если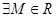
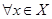 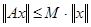 . .
Утверждение.
Для линейного нормированного пространства непрерывность линейного оператора равносильна его ограниченности.
Определение.
Наименьшая из констант M таких, что 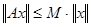 , называется нормой оператора А
и обозначается , называется нормой оператора А
и обозначается 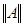 . .
В частности, выполняется 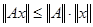 . .
Справедливо следующее утверждение: для любого ограниченного линейного оператора 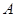 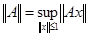 . .
§2. Пространства суммируемых функций.
Среди различных классов нормированных пространств, встречающихся в анализе, один из важнейших - это пространство суммируемых функций. Далее будем рассматривать именно эти нормированные пространства.
Определение.
Пусть 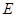 – некоторое фиксированное измеримое множество из – некоторое фиксированное измеримое множество из 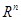 . Пространством . Пространством 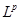 , где
, где 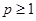 ,называется нормированное пространство, элементами которого служат функции ,называется нормированное пространство, элементами которого служат функции 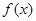 , измеримые и почти всюду конечные на , измеримые и почти всюду конечные на 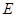 , для которых выполняется , для которых выполняется 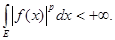
Функции, эквивалентные друг другу на 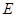 , не различаются, а считаются за один и тот же элемент пространства , не различаются, а считаются за один и тот же элемент пространства 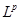 . В частности, нулевой элемент в . В частности, нулевой элемент в 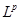 – это совокупность всех функций, равных нулю почти всюду. – это совокупность всех функций, равных нулю почти всюду.
Сложение элементов в 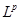 и умножение их на числа определяются как обычные сложение и умножение функций. Точнее, поскольку каждый элемент в и умножение их на числа определяются как обычные сложение и умножение функций. Точнее, поскольку каждый элемент в 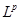 – это класс эквивалентных между собой функций, то для того, чтобы сложить два таких класса, нужно брать в них по представителю и потом суммой этих классов называют класс, содержащий сумму выбранных представителей. Результат не будет зависеть от выбора представителей в данных классах. – это класс эквивалентных между собой функций, то для того, чтобы сложить два таких класса, нужно брать в них по представителю и потом суммой этих классов называют класс, содержащий сумму выбранных представителей. Результат не будет зависеть от выбора представителей в данных классах.
Определение.
Число 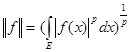 называется нормой функции называется нормой функции 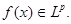
Будут выполняться все свойства нормы:
1. 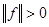 и и 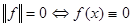 почти всюду; почти всюду;
2. 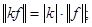
3. 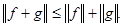
Первое свойство cледует из определения нормы и того, что 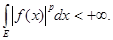
Второе – из свойства интеграла: постоянный множитель можно выносить за знак интеграла. Третье свойство вытекает из неравенства Минковского: для любых функций 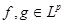

Определение.
Функция 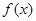 называется ограниченной почти всюду, если существует неотрицательное число называется ограниченной почти всюду, если существует неотрицательное число 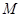 такое, что почти всюду выполняется неравенство такое, что почти всюду выполняется неравенство 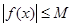 . (*) . (*)
Определение.
Пространством 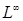 называется нормированное пространство, элементами которого служат почти всюду ограниченные функции
называется нормированное пространство, элементами которого служат почти всюду ограниченные функции 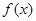 . Нормой . Нормой  называется наименьшая из констант, удовлетворяющих неравенству (*).
называется наименьшая из констант, удовлетворяющих неравенству (*).
Для  выполняется почти всюду неравенство выполняется почти всюду неравенство 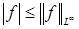 . .
Через 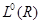 будем обозначать линейное пространство измеримых функций, заданных на R. будем обозначать линейное пространство измеримых функций, заданных на R.
Среди линейных операторов, действующих в пространстве 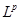 , рассмотрим следующие. , рассмотрим следующие.
Определение.
Оператор 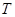 , действующий из пространства , действующий из пространства 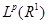 ( ( ) в ) в 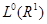 , называется оператором слабого типа (
p
,
p
)
, если , называется оператором слабого типа (
p
,
p
)
, если
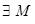 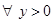 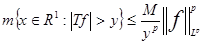 , где , где 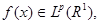 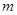 - мерамножества, и оператором типа (
p
,
p
)
, если - мерамножества, и оператором типа (
p
,
p
)
, если 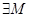 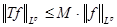 . .
По определению оператор типа 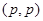 является ограниченным, что равносильно его непрерывности. является ограниченным, что равносильно его непрерывности.
Предложение 1
. Любой оператор типа 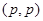 есть оператор слабого типа есть оператор слабого типа 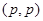 . .
Доказательство.
Нужно доказать, что 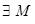 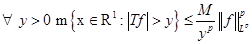 . .
Воспользуемся неравенством Чебышева: 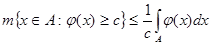 . .
Возьмем любое положительное число 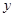 . По неравенству Чебышева . По неравенству Чебышева
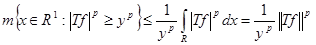 . Но по условию . Но по условию 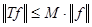 . .
Учитывая последнее соотношение, имеем 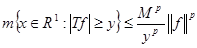 , что и требовалось доказать. , что и требовалось доказать.
§3. Интеграл Лебега – Стилтьеса.
Далее понадобится понятие интеграла Лебега – Стилтьеса. Введем это понятие.
Определение.
Пусть на R
задана монотонно неубывающая функция 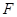 , которую для определенности будем считать непрерывной слева. Определим меры всех сегментов, интервалов и полусегментов равенствами , которую для определенности будем считать непрерывной слева. Определим меры всех сегментов, интервалов и полусегментов равенствами

Таким образом, функция 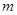 , которая каждому сегменту ставит в соответствие меру этого сегмента, будет: , которая каждому сегменту ставит в соответствие меру этого сегмента, будет:
1. принимать действительные неотрицательные значения;
2. аддитивной, т.е. мера объединения есть сумма мер этих сегментов.
Применив стандартное распространение меры, получим меру на некоторой 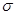 - алгебре. - алгебре.
Определение
. Меру 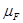 ,
получающуюся с помощью такого построения, называют мерой Лебега – Стилтьеса
, отвечающей функции ,
получающуюся с помощью такого построения, называют мерой Лебега – Стилтьеса
, отвечающей функции 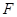 , а саму функцию , а саму функцию 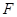 называют производящей функцией
этой меры. называют производящей функцией
этой меры.
Определение
. Пусть 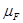 - мера на R
, порожденная монотонной функции - мера на R
, порожденная монотонной функции 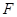 . Для этой меры обычным образом определяется класс суммируемых функций и вводится понятие интеграла Лебега . Для этой меры обычным образом определяется класс суммируемых функций и вводится понятие интеграла Лебега 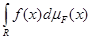 . .
Такой интеграл, взятый по мере 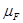 , отвечающей производящей функции , отвечающей производящей функции 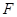 , называется интегралом Лебега – Стилтьеса
и обозначается , называется интегралом Лебега – Стилтьеса
и обозначается 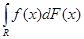 . .
Теперь докажем факт, который используется при доказательстве интерполяционной теоремы.
Предложение 2.
   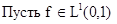 и для и для 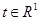
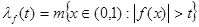 и и 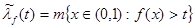 , тогда , тогда
(1) 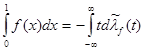 , и если , и если 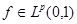 , и , и 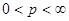 , то , то
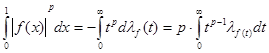 . (2) . (2)
Доказательство.
Равенство (1) следует из определения интегралов Лебега и Лебега – Стилтьеса:
Если 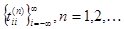 - последовательность разбиений действительной оси: - последовательность разбиений действительной оси:
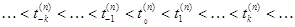 , и , и  , то интегралы , то интегралы 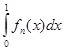 , где , где 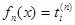 , если , если  , стремятся при , стремятся при  . .
С другой стороны:
 при при 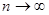 . .
Это и доказывает равенство (1).
Пусть теперь 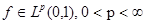 . По (1), учитывая, что . По (1), учитывая, что  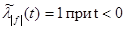 , получаем , получаем  (2’) (2’)
При 
Следовательно, из соотношения (2’), делая замену переменных 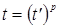 , получим первое равенство (2). , получим первое равенство (2).
Далее, для любого 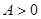 выполняется выполняется

(интегрирование по частям: 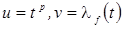 ). ).
Для доказательства второго равенства в (2) достаточно устремить в последнем соотношении число 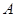 к к 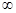 и использовать оценку: и использовать оценку:
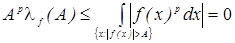 при при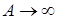 . .
Предложение 2 доказано.
Замечание.
Если функция 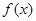 задана на задана на 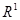 , то, применяя равенство (2) для функции , то, применяя равенство (2) для функции 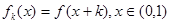 , , 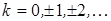 , и учитывая, что , и учитывая, что 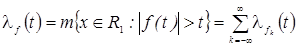 , получим , получим
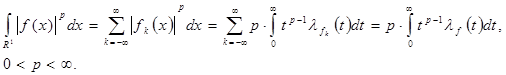 (3) (3)
Глава
II
. Интерполяция в пространствах суммируемых функций.
§1. Теорема Марцинкевича и ее применение.
Одной из важнейших в теории интерполяции является теорема Ж.Марцинкевича, доказанная им в 1939 году. Прежде чем рассмотреть теорему, докажем предложение.
Пусть дана функция 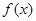 . Положим для . Положим для 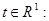
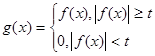 , , 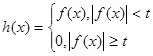 . .
Предложение 3.
Пусть 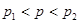 , , 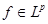 , для любого положительного числа , для любого положительного числа  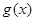 и и 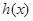 – функции, описанные выше. Тогда – функции, описанные выше. Тогда 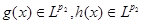 . .
Доказательство.

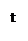 
    

Нужно показать, что 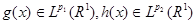 , т.е. , т.е. 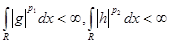 . .
I. Для функции 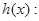
1) если 0<t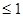 , то , то 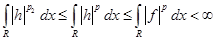 , т.к. , т.к. 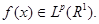
2) Пусть t>1.
Обозначим 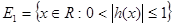 , , 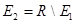 . .
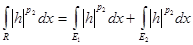 . Конечность . Конечность 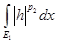 доказана в первом случае. Рассмотрим второй интеграл. доказана в первом случае. Рассмотрим второй интеграл.
Покажем, что 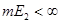 . Предположим противное, что . Предположим противное, что 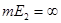 . .
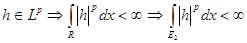 , т.к. , т.к. 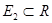 . С другой стороны, . С другой стороны, 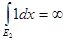 . Но . Но  на на 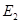 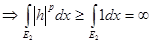 , т.е. , т.е. 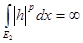 , а это противоречие. Получили, что , а это противоречие. Получили, что 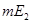 конечна и т.к. интеграл от ограниченной функции по конечной мере конечен, то конечна и т.к. интеграл от ограниченной функции по конечной мере конечен, то 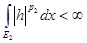 . Тогда . Тогда 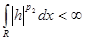 . .
II.для функции 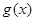 : :
1) если  , то , то 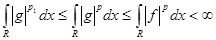 . .
2) Пусть  . .
Пусть 
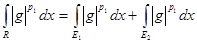 . Конечность . Конечность 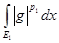 доказана в первом случае. Нужно показать, что доказана в первом случае. Нужно показать, что  конечен. конечен.
Докажем, что 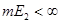 . Предположим противное, что . Предположим противное, что 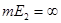 . .
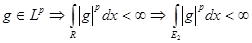 ( (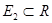 ). ).
С другой стороны  . Но . Но 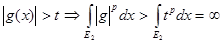 , т.е. , т.е.
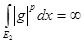 . Пришли к противоречию. . Пришли к противоречию.
Получили, что 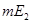 конечна и т.к. интеграл от ограниченной функции по конечной мере конечен, то конечна и т.к. интеграл от ограниченной функции по конечной мере конечен, то  . Следовательно, . Следовательно, 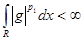 . Предложение доказано. . Предложение доказано.
Следствие.
Для всех 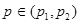 справедливо включение: справедливо включение: 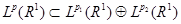 . .
Замечание 2.
Пусть оператор 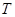 задан на пространстве задан на пространстве 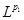 и на и на  . Тогда оператор . Тогда оператор 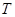 можно распространить с сохранением линейности до оператора, действующего из пространства можно распространить с сохранением линейности до оператора, действующего из пространства
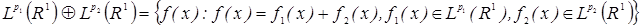 т.е. т.е.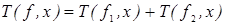 для любой функции для любой функции 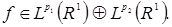
Такое определение функции 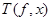 не зависит от выбора не зависит от выбора 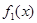 и и 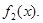 Действительно. Возьмем другое представление функции Действительно. Возьмем другое представление функции 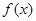 : :
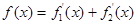 , где , где  т.е. т.е.
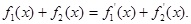 Нужно доказать, что Нужно доказать, что 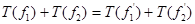 . .
Из условия следует  . Левая часть равенства – это функция из . Левая часть равенства – это функция из 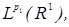 правая часть - из правая часть - из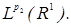 Применим к равенству оператор T: Применим к равенству оператор T:
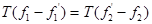 . Так как T линеен в пространствах . Так как T линеен в пространствах 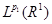 и и 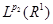 , то , то 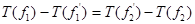 . Отсюда . Отсюда 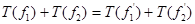 , что и требовалось доказать. , что и требовалось доказать.
Теорема Марцинкевича.
Если линейный оператор Т имеет слабый тип 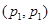 и одновременно слабый тип и одновременно слабый тип 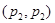 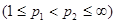 , то Т имеет тип , то Т имеет тип 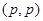 для любого для любого 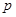 из интервала из интервала 
Доказательство.
Считаем, что 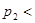 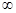 . Фиксируем функцию . Фиксируем функцию 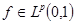 и положительное число и положительное число  . Оценим величину . Оценим величину 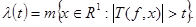
Пусть 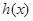 и и 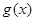 функции, описанные выше. функции, описанные выше.
Тогда  и и 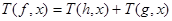 по замечанию 2. по замечанию 2.
Следовательно, 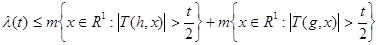 . .
Используя оценки слабого типа 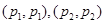 , находим, что при положительном , находим, что при положительном 

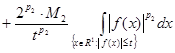 . .
Из последнего неравенства и формулы (3) из замечания 1 получаем
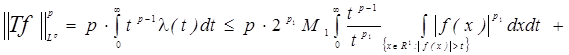
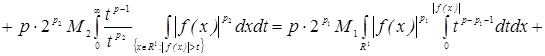
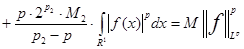 , т.е. оператор Т имеет тип , т.е. оператор Т имеет тип 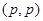 . Теорема доказана. . Теорема доказана.
В качестве применения этой теоремы рассмотрим следующий пример.
Утверждение 2.
Пусть  . Тогда оператор . Тогда оператор 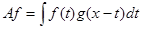 будет непрерывным оператором в пространстве будет непрерывным оператором в пространстве 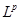 , , 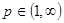 . .
Доказательство.
Рассмотрим два случая, когда 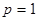 и и 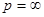 . Докажем, что оператор . Докажем, что оператор 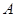 является оператором типа является оператором типа 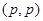 для этих случаев. Тогда по предложению 1 для этих случаев. Тогда по предложению 1 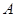 будет оператором слабого типа будет оператором слабого типа 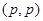 для для 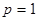 и и 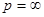 . Применив интерполяционную теорему Марцинкевича, получим, что . Применив интерполяционную теорему Марцинкевича, получим, что 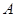 – оператор типа – оператор типа 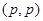 для любого для любого 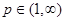 , а это равносильно его непрерывности. , а это равносильно его непрерывности.
1) 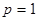 и и 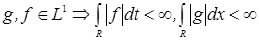 . Докажем, что найдется число . Докажем, что найдется число 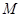 , такое, что , такое, что  
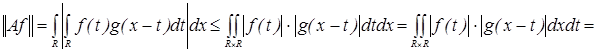

Учитывая последнее равенство и то, что для любого действительного числа  верно верно 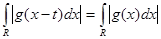 , получим , получим
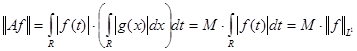 , где , где 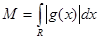 . .
2) 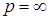 . .
Нужно доказать, что 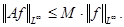
Для 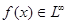 почти всюду выполняется неравенство: почти всюду выполняется неравенство:  . (*) . (*)
Обозначим 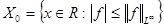 , , 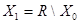 . .
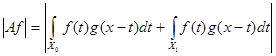 . Так как . Так как 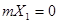 , то , то 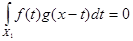 . .
Исходя из последнего соотношения и неравенства (*), получаем
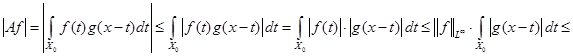
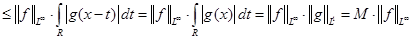 . .
Таким образом, доказали, что оператор свертки 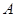 непрерывен в пространстве непрерывен в пространстве 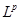 для любого р
³1. для любого р
³1.
§2. Интерполяционная теорема Рисса – Торина
и ее применение.
Прежде чем рассмотреть теорему Рисса – Торина и ее приложение, приведем определения и докажем факты, связанные с теорией банаховых пространств, которые понадобятся для этого.
Определение
. Последовательность 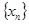 метрического пространства Х называется фундаментальной
, если метрического пространства Х называется фундаментальной
, если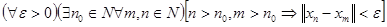 . .
Верно следующее утверждение.
Утверждение
. Если последовательность 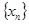 сходится, то она фундаментальная. сходится, то она фундаментальная.
Обратно верно не всегда.
Определение
. Метрическое пространство 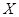 называется полным
,
если в нем любая фундаментальная последовательность сходится. называется полным
,
если в нем любая фундаментальная последовательность сходится.
Определение
. Если пространство 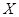 , порожденное нормой, является полным, то линейное нормированное пространство называется банаховым
. , порожденное нормой, является полным, то линейное нормированное пространство называется банаховым
.
Определение.
Пусть 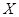 – банахово пространство, – банахово пространство, 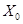 – подпространство в – подпространство в 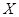 . . 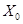 называется всюду плотным в
Х
,
если называется всюду плотным в
Х
,
если 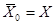 , т.е. , т.е. 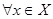 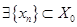 , такая, что , такая, что 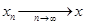 . .
Утверждение 4
. Пусть оператор 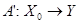 , где , где 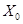 плотно в плотно в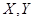 – банахово пространство. Тогда оператор – банахово пространство. Тогда оператор 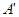 можно распространить на можно распространить на 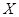 , т.е. существует оператор , т.е. существует оператор 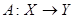 , такой, что , такой, что 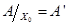 и и 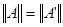 . .
Доказательство.
Возьмем 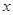 из из 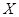 . По определению существует последовательность . По определению существует последовательность 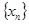 из из 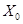 такая, что такая, что 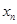 стремится к стремится к 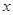 , при , при 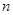 стремящемся к стремящемся к 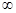 . .
Докажем, что 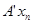 из из 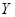 будет фундаментальной последовательностью. Тогда, т.к. будет фундаментальной последовательностью. Тогда, т.к. 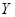 полное, последовательность полное, последовательность 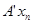 будет сходящейся. будет сходящейся.
Возьмем произвольное положительное число 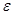 . Найдем номер . Найдем номер 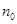 , для которого выполняется , для которого выполняется 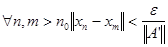 .Тогда .Тогда
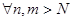 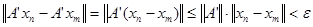 . Следовательно, последовательность . Следовательно, последовательность 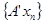 фундаментальная. фундаментальная.
Пусть 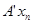 стремится к стремится к 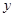 . Определим оператор . Определим оператор 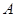 равенством равенством 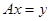 . .
а) Проверим корректность определения оператора 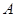 . .
Итак, 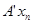 стремится к стремится к 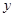 , , 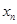 стремится к стремится к 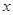 . Возьмем другую последовательность . Возьмем другую последовательность 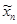 , имеющую в пределе , имеющую в пределе 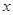 . Тогда . Тогда 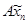 будет стремится к некоторому элементу будет стремится к некоторому элементу 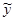 .Составим новую последовательность .Составим новую последовательность  Ее пределом будет Ее пределом будет 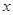 . Пусть соответствующая последовательность . Пусть соответствующая последовательность 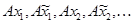 стремится к стремится к 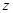 . Из последней можно выбрать две подпоследовательности . Из последней можно выбрать две подпоследовательности  и и 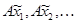 , сходящиеся соответственно к , сходящиеся соответственно к 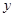 и и 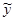 .Следовательно, .Следовательно, 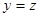 и и 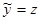 , т.е. , т.е. 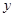 и и 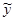 совпадают. совпадают.
б) Докажем линейность оператора А. Пусть  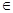 Х; Х;  - произвольные числа. Рассмотрим элемент - произвольные числа. Рассмотрим элемент 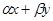 . По определению существуют последовательности {xn
},{yn
}, такие, что . По определению существуют последовательности {xn
},{yn
}, такие, что  . Тогда . Тогда 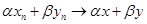 . .
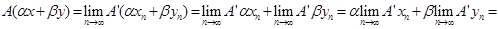 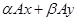 . .
Получили 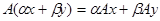 , что и означает по определению линейность оператора А. При этом, т.к. если , что и означает по определению линейность оператора А. При этом, т.к. если  , то в качестве , то в качестве 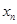 можно взять можно взять 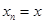 для всех n
. Тогда для всех n
. Тогда  и и 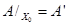 . .
в) Докажем непрерывность оператора А.
Возьмем 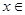 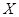 . . 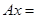 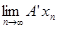 , , 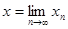 . .
  . По теореме о предельном переходе в неравенстве будет выполняться неравенство . По теореме о предельном переходе в неравенстве будет выполняться неравенство  . Т.к. по определению . Т.к. по определению 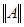 - это наименьшая из констант, удовлетворяющих данному неравенству, то - это наименьшая из констант, удовлетворяющих данному неравенству, то 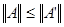 . (*) . (*)
С другой стороны, по определению 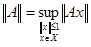 , , 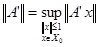 . Так как . Так как 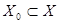 , то , то 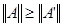 . (**) . (**)
Учитывая неравенства (*) и (**) , установили равенство 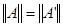  . Таким образом, утверждение доказано. . Таким образом, утверждение доказано.
Определение
. Функция 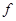 называется простой
, если она представляет собой конечную линейную комбинацию характеристических функций попарно непересекающихся измеримых множеств называется простой
, если она представляет собой конечную линейную комбинацию характеристических функций попарно непересекающихся измеримых множеств 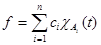 , где , где 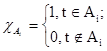 . .
Теорема Лебега
. Если последовательность 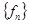 на на 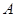 сходится к сходится к 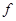 и при всех и при всех 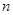  , где , где 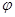 суммируема на суммируема на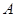 , то предельная функция , то предельная функция 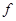 суммируема на суммируема на 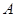 и и 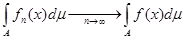 . .
Предложение 4
. Множество простых функций всюду плотно в 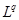 , т.е. , т.е. 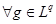 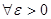  , такая, что , такая, что 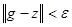 ,где ,где  – простая функция. – простая функция.
Доказательство.
I.Обозначим 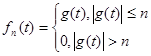 , где , где 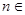 N
. N
.
Ясно, что для почти всех  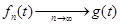 . Тогда . Тогда  для почти всех для почти всех  . Следовательно, . Следовательно, 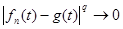 . .
С другой стороны, 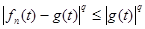 (*) (*) 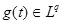 ,т.е. ,т.е. 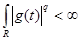 . Поэтому . Поэтому 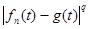 суммируема. Применим теорему Лебега к неравенству (*) : суммируема. Применим теорему Лебега к неравенству (*) :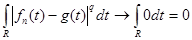 . Получим, что . Получим, что 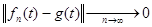 и, значит, приблизили и, значит, приблизили 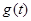 функциями функциями 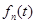 . Возьмем произвольное положительное число . Возьмем произвольное положительное число 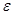 . Найдем функцию . Найдем функцию 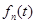 такую, что такую, что 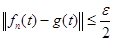 . .
II. Приблизим 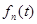 ступенчатой функцией. ступенчатой функцией.
Обозначим 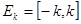 , где , где 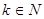 . Положим . Положим 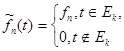 . .
По свойству интеграла Лебега для любого положительного 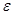 найдется найдется 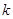 , такое, что , такое, что 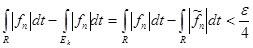 . Это означает, что . Это означает, что 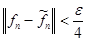 . .
Отрезок 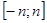 разобьем на разобьем на 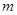 равных частей точками равных частей точками 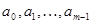 так, чтобы так, чтобы 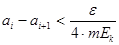 . .
Обозначим 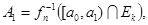 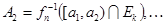
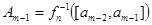 . .
Рассмотрим функцию  . Тогда . Тогда 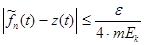 . Следовательно, . Следовательно,  , т.е. , т.е. 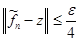 . .
В результате нашлась простая функция 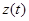 такая, что такая, что
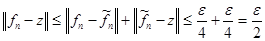 . .
III. Таким образом, 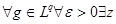 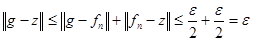 . Предложение доказано. . Предложение доказано.
Первая интерполяционная теорема в теории операторов была получена М.Риссом в 1926 году в виде некоторого неравенства для билинейных форм. Ее уточнение и операторная формулировка были даны Г.О.Ториным. Вся теория интерполяции линейных операторов первоначально развивалась в направлении обобщения этой теоремы. Дадим ее формулировку.
Теорема.
Пусть 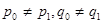 . Оператор Т действует из пространства . Оператор Т действует из пространства 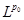 в в 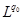 с нормой с нормой 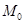 и одновременно из и одновременно из 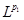 в в 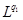 с нормой с нормой 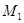 .Тогда Т будет непрерывным оператором из пространства .Тогда Т будет непрерывным оператором из пространства 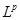 в в 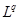 с нормой с нормой 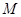 , удовлетворяющей неравенству , удовлетворяющей неравенству 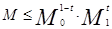 при условии, что 0<t<1 и при условии, что 0<t<1 и 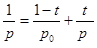 ; ; 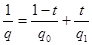 . .
Теперь рассмотрим приложение теоремы Рисса – Торина в доказательстве следующего факта.
Теорема.
Пусть 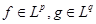 и для чисел и для чисел 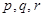 выполняется равенство выполняется равенство 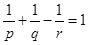 .Тогда свертка .Тогда свертка 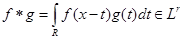 . .
Доказательство.
Нужно доказать, что 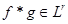 , т.е. , т.е. 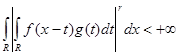 . Зафиксируем произвольную функцию . Зафиксируем произвольную функцию 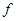 из из 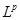 . Докажем сначала требуемый результат для частного случая, когда функция g простая, а затем распространим на произвольные функции g. . Докажем сначала требуемый результат для частного случая, когда функция g простая, а затем распространим на произвольные функции g.
I. Пусть функция 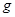 простая. простая.
1) Рассмотрим оператор свертки на множестве простых функций и проверим, что он типа 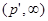 , где , где 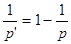 . В силу неравенства Гельдера . В силу неравенства Гельдера 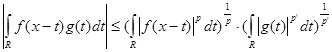 . Учитывая геометрический смысл . Учитывая геометрический смысл  интеграла, получим интеграла, получим 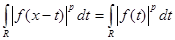 для любого действительного числа х. Тогда для любого действительного числа х. Тогда 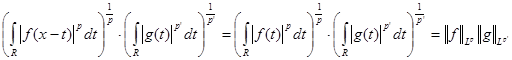 . Так как . Так как 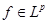 , то , то 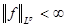 , т.е. равна некоторому числу , т.е. равна некоторому числу 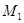 . Таким образом, . Таким образом, 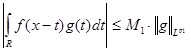 . Следовательно, нашлась константа . Следовательно, нашлась константа 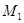 , такая, что , такая, что 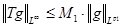 . Это и означает, что оператор свертки Т на множестве простых функций типа . Это и означает, что оператор свертки Т на множестве простых функций типа 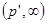 . .
2) Проверим, что оператор Т типа 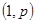 , т.е. , т.е. 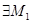 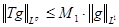 . .
Рассмотрим случай, когда функция g имеет вид:  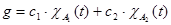 . .

 . .
Обозначим  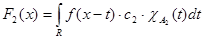 . .
Тогда правая часть равенства примет вид 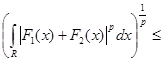
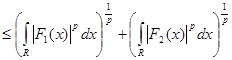  по неравенству Минковского. (1) по неравенству Минковского. (1)
Рассмотрим первое слагаемое 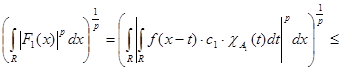 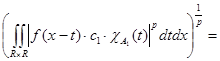
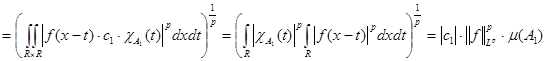 (2) Аналогично второе слагаемое (2) Аналогично второе слагаемое
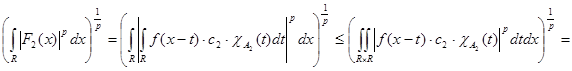
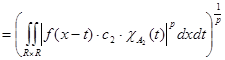 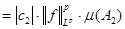 . (3) . (3)
Таким образом, учитывая (1),(2),(3), получим 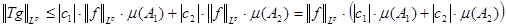 . Найдем . Найдем
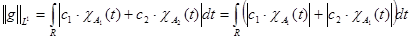 , т.к. , т.к. 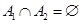 . .
Далее имеем
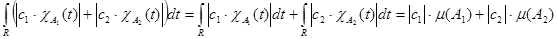 . В результате, . В результате, 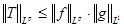 ,т.к. ,т.к. 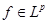 , то , то 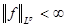 и равна некоторому числу и равна некоторому числу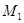 . .
Совершенно аналогично доказывается 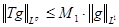 для случая, когда для случая, когда 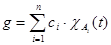 . .
1) Таким образом, из пунктов I.1 и I.2 получим, что 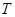 типа типа 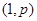 и и  , и, , и,
следовательно, 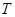 будет типа будет типа 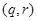 при условии при условии 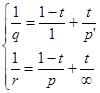 , где , где 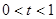 . .
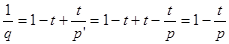 ; ;  , т.е. , т.е. 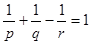 , что и дано по условию. , что и дано по условию.
Таким образом, применив теорему Рисса – Торина, установили истинность доказываемого утверждения для всех простых функций 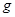 . .
II. Пусть 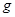 – произвольная функция из – произвольная функция из 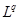 . .
По предложению 4 множество простых функций всюду плотно в 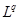 . .
По утверждению 4 оператор свертки 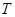 можно распространить на можно распространить на 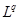 и тогда доказываемый факт верен для любой функции и тогда доказываемый факт верен для любой функции 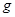 из из 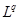 . Теорема доказана. . Теорема доказана.
Глава
III
. Пространства суммируемых последовательностей.
§1. Основные понятия.
Рассмотрим применение теории интерполяции для пространств 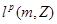 . .
Пусть {m
z
}z
Î
Z
- последовательность неотрицательных чисел. Определим на множестве Z
меру следующим образом: 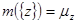 для любого целого числа для любого целого числа 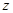 . Пространство суммируемых со степенью p
последовательностей относительно меры m
, то есть таких, что
. Пространство суммируемых со степенью p
последовательностей относительно меры m
, то есть таких, что 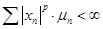 обозначается обозначается 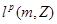 . .
Так как мера m
определена на множестве всех подмножеств множества Z
, то любую последовательность можно рассматривать как измеримую функцию. Обозначим через 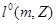 линейное пространство всех последовательностей. линейное пространство всех последовательностей.
Определение
. Число 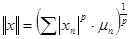 называется нормой последовательности
xn
из
lp
(
m
,
Z
). называется нормой последовательности
xn
из
lp
(
m
,
Z
).
В случае, если 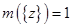 для всех z
, то получим классическое пространство lp
(
Z
)
последовательностей, суммируемых со степенью p
. для всех z
, то получим классическое пространство lp
(
Z
)
последовательностей, суммируемых со степенью p
.
Определение
. Оператор Т, действующий из пространства 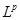 в в 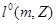 называется оператором слабого типа (
p
,
p
)
, если называется оператором слабого типа (
p
,
p
)
, если 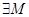 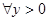 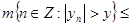 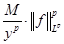 , где , где 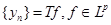 , и оператором типа
(
p
,
p
)
, если , и оператором типа
(
p
,
p
)
, если 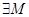 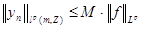 . .
В этом случае остается справедливым следующий факт: любой оператор типа 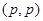 есть оператор слабого типа есть оператор слабого типа 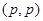 . Прежде чем установить его истинность, докажем утверждение, которое для этого понадобится. . Прежде чем установить его истинность, докажем утверждение, которое для этого понадобится.
Утверждение 5
. Пусть дана последовательность 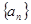 из из  с неотрицательными членами. Тогда с неотрицательными членами. Тогда 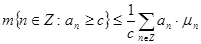 . .
Доказательство.
Обозначим 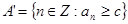 . Нужно доказать, что . Нужно доказать, что 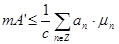 . .
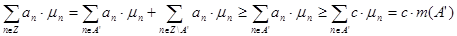 . Получили, что . Получили, что 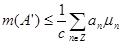 . .
Утверждение доказано.
Предложение 5
. Любой оператор типа 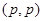 есть оператор слабого типа есть оператор слабого типа 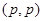 . .
Доказательство
.
Дано, что 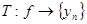 и и 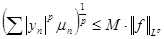 . Доказать, что . Доказать, что 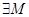 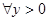
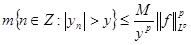 . .
Возьмем произвольное положительное число 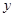 . По утверждению 5 . По утверждению 5
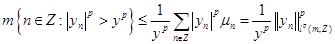 . По условию . По условию 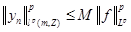 . Тогда . Тогда 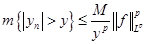 , что и требовалось доказать. , что и требовалось доказать.
Легко увидеть, что теорема Марцинкевича будет справедлива и для операторов, действующих из пространств 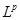 в пространство в пространство 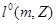 . .
§2. Связь между коэффициентами Фурье 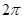 - периодической функции и ее нормой в - периодической функции и ее нормой в 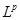 . .
Теория интерполяции имеет многочисленные приложения в теории рядов Фурье.
Определение
. Пусть  -периодическая функция, такая что -периодическая функция, такая что 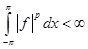 . Нормой . Нормой 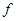 в пространстве в пространстве 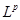 называется число
называется число 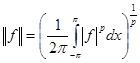 , а коэффициентами Фурье функции , а коэффициентами Фурье функции
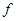 называются числа называются числа 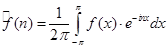 . .
Для функций 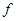 из пространства из пространства 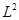 выполняется равенство выполняется равенство 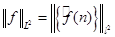 . .
В случае других значений 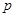 это, вообще говоря, не верно. Однако можно указать следующую оценку. это, вообще говоря, не верно. Однако можно указать следующую оценку.
Предложение 6
. Пусть  периодическая функция из периодическая функция из 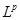 . Тогда для любого числа . Тогда для любого числа 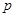 из отрезка [1,2] существует константа из отрезка [1,2] существует константа 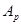 , такая, что , такая, что 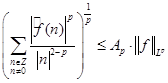 . .
Доказательство.
Рассмотрим оператор 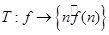 и определим меру и определим меру 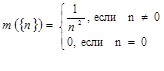 , т.е. оператор , т.е. оператор 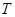 действует из действует из 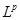 в в 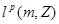 . .
1) Докажем, что 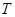 оператор слабого типа оператор слабого типа 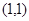 : : 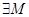 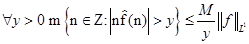 . .
Зафиксируем произвольное положительное число 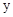 . .
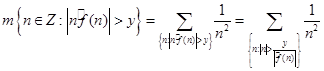 . .
Пусть 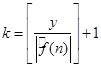 . Тогда . Тогда 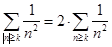 . (2) . (2)
Далее имеем
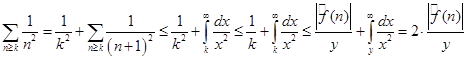 . .
Учитывая равенства (1) и (2), получим, что 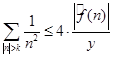 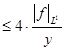 . .
В результате нашли константу 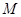 , такую, что , такую, что 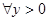 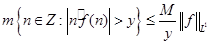 . .
2) Докажем, что 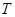 типа типа 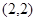 : : 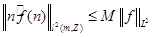 . .
Уже говорилось, что для функций из пространства 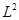 выполняется равенство выполняется равенство 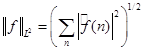 . (3) . (3)
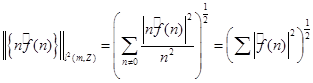 . По неравенству (3) . По неравенству (3) 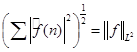 . По предложению 5 оператор . По предложению 5 оператор 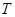 будет слабого типа будет слабого типа 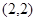 . .
3) По теореме Марцинкевича 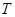 будет типа будет типа 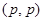 для любого для любого 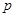 из интервала (1,2), т.е. из интервала (1,2), т.е. 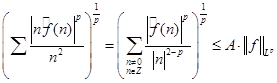 , что и требовалось доказать. , что и требовалось доказать.
Литература.
1. Вулих Б.З. Краткий курс теории функций вещественной переменной. «Наука», Москва, 1965.
2. Кашин Б.С., Саакян А.А. Ортогональные ряды. «Наука», Москва, 1984.
3. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. «Наука», Москва, 1968.
4. Крейн С.Г., Петунин Ю.И., Семенов Е.М. Интерполяция линейных операторов.«Наука», Москва, 1978.
5. Натансон И.П. Теория функций вещественной переменной. «Наука», Москва, 1974.
Распространим меру с сохранением свойств 1 и 2, определенную пока для сегментов, на более широкий класс множеств – так называемые элементарные множества.
Назовем множество элементарным
, если его можно представить хотя бы одним способом как объединение конечного числа попарно непересекающихся сегментов.
Определим теперь меру 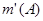 для элементарных множеств следующим образом: если для элементарных множеств следующим образом: если 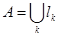 , где , где 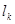 - попарно непересекающиеся сегменты, то - попарно непересекающиеся сегменты, то 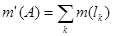 . .
Далее распространим меру и на бесконечные объединения сегментов. Для того, чтобы при этом не встречались множества «бесконечной меры», ограничимся рассмотрением множеств, целиком принадлежащих отрезку 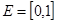 . На совокупности всех таких множеств определим две функции . На совокупности всех таких множеств определим две функции 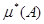 и и 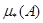 : :
Определение. Верхней мерой 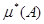 множества множества 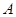 называется число, где нижняя грань берется по всевозможным покрытиям множества А конечными или счетными системами сегментов.
называется число, где нижняя грань берется по всевозможным покрытиям множества А конечными или счетными системами сегментов.
Определение. Нижней мерой 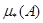 множества множества
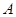 называетсячисло называетсячисло 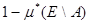 . .
Определение.
Множество 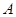 называется измеримым
, если называется измеримым
, если 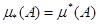 . Их общее значение . Их общее значение 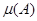 называется лебеговской мерой
. называется лебеговской мерой
.
Итак, распространили меру с элементарных множеств на более широкий класс множеств, называемых измеримыми
, замкнутый относительно операций взятия счетных сумм и пересечений. Построенная мера является на этом классе множеств 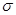 - аддитивной, т.е. если - аддитивной, т.е. если 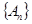 - последовательность попарно непересекающихся измеримых множеств и - последовательность попарно непересекающихся измеримых множеств и 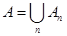 , то , то 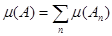 . .
Однако, мы рассмотрели лишь те множества, которые являются подмножествами 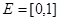 . .
Нетрудно освободиться и от этого ограничения. Представив всю числовую ось как сумму отрезков 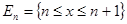 ( ( - целое), будем говорить, что множество - целое), будем говорить, что множество 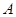 измеримо, если его пересечение измеримо, если его пересечение 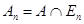 с каждым из этих отрезков измеримо, и ряд с каждым из этих отрезков измеримо, и ряд 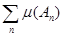 сходится. При этом положим по определению, сходится. При этом положим по определению, 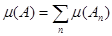 . .
Причем совокупность множеств, измеримых относительно данной меры, также будет замкнута относительно операций взятия счетных сумм и пересечений, а мера будет 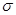 - аддитивна. - аддитивна.
Определение.
Меру 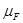 , получающаяся с помощью такого построения, называют мерой Лебега – Стилтьеса
, отвечающей функции , получающаяся с помощью такого построения, называют мерой Лебега – Стилтьеса
, отвечающей функции 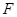 , а саму функцию , а саму функцию 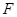 называют производящей функцией
этой меры. называют производящей функцией
этой меры.
|