Курсовая работа
по дисциплине «Алгоритмы с оценками»
На тему «Труднорешаемые задачи. Последовательный анализ вариантов»
Содержание
Введение
1. Задачи, NP-трудные в сильном смысле
1.1. Обслуживание требований без задержек
2.Алгоритм
2.1 Последовательный анализ вариантов
3. Псевдополиномиальное сведение задач и NP-трудные в сильном смысле задачи
4.Использование NP-трудных задач
Заключение
Библиографический список
Введение
Большинство задач, интересных с практической точки зрения, имеют полиномиальные (работающие за полиномиальное время) алгоритмы решения. То есть время работы алгоритма на входе длины n составляет не более O(nk) для некоторой константы k (не зависящей от длины входа). Разумеется, не каждая задача имеет алгоритм решения, удовлетворяющий этому свойству. Некоторые задачи вообще не могут быть решены никаким алгоритмом. Классический пример такой задачи — «проблема остановки» (выяснить останавливается ли данная программа на данном входе). Кроме того, бывают задачи, для которых существует решающий их алгоритм, но любой такой алгоритм работает «долго» — время его работы не есть O(nk) ни для какого фиксированного числа k.
Если мы хотим провести пусть грубую, но формальную границу между «практическими» алгоритмами и алгоритмами, представляющими лишь теоретический интерес, то класс алгоритмов, работающих за полиномиальное время, является разумным первым приближением. Мы рассмотрим, руководствуясь [1], класс задач, называемых NP-полными. Для этих задач не найдены полиномиальные алгоритмы, однако и не доказано, что таких алгоритмов не существует. Изучение NP-полных задач связано с так называемым вопросом «P = NP». Этот вопрос был поставлен в 1971 году и является сейчас одной из наиболее сложных проблем теории вычислений.
Зачем программисту знать о NP-полных задачах? Если для некоторой задачи удается доказать ее NP-полноту, есть основания считать ее практически неразрешимой. В этом случае лучше потратить время на построение приближенного алгоритма, чем продолжать искать быстрый алгоритм, решающий ее точно.
1. Задачи, NP-трудные в сильном смысле
Приводятся примеры доказательств NP-трудности в сильном смысле ряда задач теории расписаний. Техника доказательства результатов такого рода во многом напоминает приемы которые использовались при установлении NP трудности (в обычном смысле) экстремальных задач теории расписаний. Для доказательства NP-трудности в сильном смысле тон или иной экстремальной задачи будем доказывать №" трудность в сильном смысле соответствующей задачи распознавания. Для этого достаточно показать, что к ней сводится некоторая известная NP –полная в сильном смысле задача. В качестве такой задачи в данном параграфе выбрана задача о 3-разбиении,
которая заключается в следующем. Имеется множество  каждому элементу которого поставлено в соответствие натуральное число (вес) е,, причем каждому элементу которого поставлено в соответствие натуральное число (вес) е,, причем 
Существует ли такое разбиение мужества .V0
на трехэлементные подмножества N
°,
N
*
.....N°
такие, что  для всех ; для всех ; 
Отметим, что условие  является существенным. Оно означает, что сумма весов любых четырех (и более) элементов будет больше, чем Е. а любых двух элементов - меньше, чем Е.
Подчеркнем также то, что задача о разбиении - исторически первая задача, для которой установлена W-полнота в сильном смысле. является существенным. Оно означает, что сумма весов любых четырех (и более) элементов будет больше, чем Е. а любых двух элементов - меньше, чем Е.
Подчеркнем также то, что задача о разбиении - исторически первая задача, для которой установлена W-полнота в сильном смысле.
Чтобы обеспечить псевдополиномиальное сведение задачи с 3-раэбнении к некоторой задаче распознавания, необходимо преобразовать входную информацию задачи о 3-разбиении во входную информацию некоторой ее индивидуальной задачи распознавания. Число выполняемых при этом действий должно полиномиально зависеть от длины входа задачи о 3 разбиении, представленного в унарной системе счисления, другими словами, от величины  Иногда удается установить обычную полиномиальную сводимость. В этом случае число действий но преобразованию входной информации полиномиально зависит от Иногда удается установить обычную полиномиальную сводимость. В этом случае число действий но преобразованию входной информации полиномиально зависит от  или даже от n0
. Построенная в результате преобразования входа задачи о З разбиении –индивидуальная задача распознавания должна иметь ответ тогда и только тогда, когда такой же ответ имеет задача о 3 разбиений. или даже от n0
. Построенная в результате преобразования входа задачи о З разбиении –индивидуальная задача распознавания должна иметь ответ тогда и только тогда, когда такой же ответ имеет задача о 3 разбиений.
1.1 Обслуживание требований без задержек
Установим NP трудность в
сильном смысле  В этой задаче условие означает что требование I не обслуживается прибором LПри такой интерпретации нулевых длительностей оптимальное расписание без задержек необязательно принадлежит классу перестановленных расписаний . В этой задаче условие означает что требование I не обслуживается прибором LПри такой интерпретации нулевых длительностей оптимальное расписание без задержек необязательно принадлежит классу перестановленных расписаний .
Другими — словами, задачи  и
и  в данном случае не эквивалентны. Напомним, что задачи в данном случае не эквивалентны. Напомним, что задачи  и и  эквивалентны, если все эквивалентны, если все  либо среди f.t
имеются равные нулю и запись либо среди f.t
имеются равные нулю и запись  означает, что длительность. Справедлива
означает, что длительность. Справедлива
Теорема 1.1.
Задача  является NPтрудной в сильном смысле, если условие является NPтрудной в сильном смысле, если условие  означает, что требование i
прибором L
не обслуживается.
означает, что требование i
прибором L
не обслуживается.
Доказательство.
Сформулируем соответствующую задачу распознавания: определить, существует ли расписание s
°,
при котором  для заданного числа у. Покажем, что к этой задаче сводится задача о 3-разбиении. Для преобразования входной информации задачи о 3-раэбиении во входную информацию индивидуальной задачи распознавания необходимо значения для заданного числа у. Покажем, что к этой задаче сводится задача о 3-разбиении. Для преобразования входной информации задачи о 3-раэбиении во входную информацию индивидуальной задачи распознавания необходимо значения  и у
выразить через
и у
выразить через 
Положим  и разобьем множество N
на две группы: и-требования, обозначаемые Uij
и разобьем множество N
на две группы: и-требования, обозначаемые Uij
 и v-требовання, обозначаемые и v-требовання, обозначаемые 
Положим   , и зададим / , и зададим / . Покажем, что в построенной задаче расписание S
°
, при котором . Покажем, что в построенной задаче расписание S
°
, при котором  существует тогда и только тогда, когда имеет решение задача о 3-разбиеиии. имеет решение задача о 3 разбиений. существует тогда и только тогда, когда имеет решение задача о 3-разбиеиии. имеет решение задача о 3 разбиений.
1.
Пусть задача о 3-разбиении имеет решение и   найденные трехэлементные подмножества элементов множества N
0
. Через найденные трехэлементные подмножества элементов множества N
0
. Через  обозначим произвольную перестановку u-требований с номерами из множества
обозначим произвольную перестановку u-требований с номерами из множества  . Прибор 1 функционирует без простоев во временном интервале . Прибор 1 функционирует без простоев во временном интервале 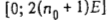 ], а прибор 2 - в интервале [0; у]. При этом прибор 1 в интервале ], а прибор 2 - в интервале [0; у]. При этом прибор 1 в интервале 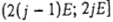 обслуживает требование обслуживает требование  . Прибор 2 в интервале . Прибор 2 в интервале 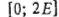 обслуживает требование v
0
, а в каждом из интервалов обслуживает требование v
0
, а в каждом из интервалов 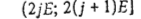 -
последовательность требований -
последовательность требований  Требование Требование  обслуживается прибором 2 в интервале обслуживается прибором 2 в интервале 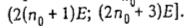
2. Пусть существует расписание s
°
. Так как 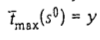 и прибор 2 функционирует в интервале [0; у] без простоев. и прибор 2 функционирует в интервале [0; у] без простоев.

Рис.(1.1)
Прибор 1 завершает обслуживание всех требований не раньше момента времени у - Е.
С учетом того, что задержки запрещены, последним требованием, которое обслуживает прибор 2, будет некоторое v-требование, а прибор 1 должен функционировать без простоев в интервале 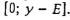 . Поскольку требования . Поскольку требования 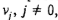 , не отличаются друг от друга по длительностям обслуживания, не нарушая общности можно считать, что они обслуживаются прибором I в порядке возрастания их номеров. Отсюда сразу следует, что требования , не отличаются друг от друга по длительностям обслуживания, не нарушая общности можно считать, что они обслуживаются прибором I в порядке возрастания их номеров. Отсюда сразу следует, что требования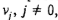 , обслуживаются при расписании s
°
так же, как и при расписании, представленном на рис. 1.1. Требование vc
обслуживается прибором 2 в интервале , обслуживаются при расписании s
°
так же, как и при расписании, представленном на рис. 1.1. Требование vc
обслуживается прибором 2 в интервале 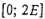 , так как это единственный незанятый подинтервал длины 2Е интервала , так как это единственный незанятый подинтервал длины 2Е интервала  Требования щ
должны обслуживаться прибором 2 в интервалах Требования щ
должны обслуживаться прибором 2 в интервалах 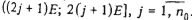 . Обозначая через . Обозначая через 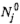 множество номеров и-требований, обслуживаемых прибором 2 в интервале множество номеров и-требований, обслуживаемых прибором 2 в интервале 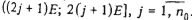 , получаем решение задача о 3-разбиении. Тем самым за , получаем решение задача о 3-разбиении. Тем самым за 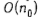 действий задача о 3-раз-биении сведена к задаче о существовании расписания S
°.
Теорема доказана.
действий задача о 3-раз-биении сведена к задаче о существовании расписания S
°.
Теорема доказана.
Теорема 2
. Задача  является NP-трудной в сильном смысле. является NP-трудной в сильном смысле.
Теорема 3.
Задача 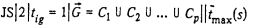 является NP-трудной в сильном смысле. является NP-трудной в сильном смысле.
Доказательство.
Сформулируем соответствующую задачу распознавания. В обслуживающую систему, состоящую из двух приборов А и В, в момент времени d
=0
поступает частично упорядоченное множество требований
N
{1,2...., л}.
. Каждая компонента связности графа редукции отношения -, заданного на N
,
является цепью. Длительность выполнения каждой операции равна единице. Требуется определить, существует ли расписание S
°
, при котором 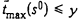 для заданного значения у
. для заданного значения у
.
Построим псевдополнномиальное сведение задачи о 3-разбиении к сформулированной задаче распознавания.
Положим: 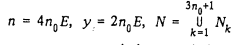 , где , где
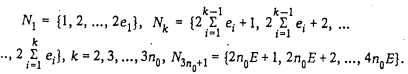
На множестве N заладим отношение -, полагай / -
I
тогда и только тогда, когда 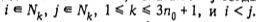 .
Очевидно, каждая компонента связности графа редукции этого отношения представляет собой цепь.
.
Очевидно, каждая компонента связности графа редукции этого отношения представляет собой цепь.
Пусть процесс обслуживания каждого требования 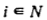 состоит в выполнении единственной операции. Для требований из множества N
1
положим L
1
= (В) при
состоит в выполнении единственной операции. Для требований из множества N
1
положим L
1
= (В) при 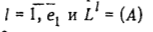 . Для каждого . Для каждого 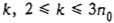 , положим
, положим
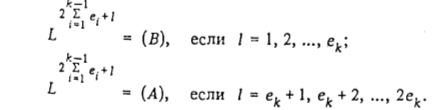
Для требования из множества 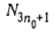 - линейно –упорядоченное и число его элементов равно - линейно –упорядоченное и число его элементов равно 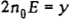 , то при любом расписаний с общим временем обслуживания требований, равным у, требования множества N3
n
+1
должны обслуживаться непрерывно одно за другим начиная с момента времени d
= 0. На рис. 2 представлен фрагмент расписания обслуживания требований множества , то при любом расписаний с общим временем обслуживания требований, равным у, требования множества N3
n
+1
должны обслуживаться непрерывно одно за другим начиная с момента времени d
= 0. На рис. 2 представлен фрагмент расписания обслуживания требований множества 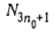 при котором общее время обслуживания требований равно у. Это расписание является периодическим с периодом при котором общее время обслуживания требований равно у. Это расписание является периодическим с периодом 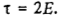

Рис(1.2)
Таким образом, обслуживание требований множества 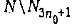 при любом расписании с общим временем обслуживания требований, равным у, может быть осуществлено только в тех единичных интервалах, которые определяются последовательностью при любом расписании с общим временем обслуживания требований, равным у, может быть осуществлено только в тех единичных интервалах, которые определяются последовательностью 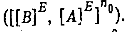
Покажем, что расписание S
0
можно построить тогда и только тогда, когда имеет решение задача о 3-раэбиении. Пусть существует разбиение множества № на n0
трехэлементных подмножеств 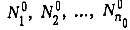 таких, что таких, что 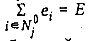 при j=1,0. Тогда, обслуживая множество требований при j=1,0. Тогда, обслуживая множество требований 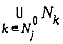 интервале
интервале 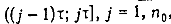 , в соответствии с отношением получаем расписание с общим временем обслуживания требований, равным у
. , в соответствии с отношением получаем расписание с общим временем обслуживания требований, равным у
.
Пусть существует расписание S
°
, при котором 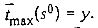 .Так как суммарная длительность обслуживания всех требований прибором А
(прибором В)
равна у
, то при расписании S
как прибор А,
так и прибор В
в интервале [0; у] не простаивает. По условию обслуживание каждого требования .Так как суммарная длительность обслуживания всех требований прибором А
(прибором В)
равна у
, то при расписании S
как прибор А,
так и прибор В
в интервале [0; у] не простаивает. По условию обслуживание каждого требования 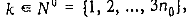 для которого для которого 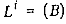
Учитывая, что в построенном при доказательстве теоремы 3 примере процесс обслуживания каждого требования  состоит из единственной операции, можно сделать вывод о том, что и задача состоит из единственной операции, можно сделать вывод о том, что и задача 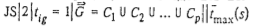 является NP-трудной в сильном смысле. является NP-трудной в сильном смысле.
2. Алгоритм
Этап 1.
Построить бесконтурный граф 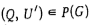 в результате выполнения следующего шага не более чем q - 1 раз. Первоначально положить в результате выполнения следующего шага не более чем q - 1 раз. Первоначально положить 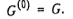
Пусть после выполнения 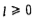 шагов получен смешанный граф шагов получен смешанный граф 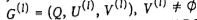 , у которого l
вершин отмечено и существует неотмеченная вершина i,
в которую не заходит ни одна дуга, исходящая из неотмеченной вершины. (Если такой вершины нет, то в графе (Q,U) содержится контур. Конец.) , у которого l
вершин отмечено и существует неотмеченная вершина i,
в которую не заходит ни одна дуга, исходящая из неотмеченной вершины. (Если такой вершины нет, то в графе (Q,U) содержится контур. Конец.)
Шаг 1 + 1.
Отметить вершину i
и в случае, если в графе G(1)
есть ребра, инцидентные этой вершине, то заменить их исходящими из нее дугами. Полученный в результате граф обозначить G(J+1)
= (Q,
U
(
l
+1),
V(
l
+1)
).
Если V(
l
+1)
= 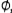 , то бесконтурный граф построен: , то бесконтурный граф построен: 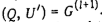 . В противном случае выполнить этот шаг, заменив l на l + 1. . В противном случае выполнить этот шаг, заменив l на l + 1.
Этап 2
. В соответствии с алгоритмом 3.1 построить которое допустимо относительно ориентированного графа 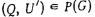 и смешанного графа G. Конец. и смешанного графа G. Конец.
Нетрудно убедиться в корректности описанного алгоритма, что и завершает доказательство теоремы .
Очевидно, трудоемкость этапа 1
алгоритма не превосходит 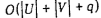 и, следовательно, общая трудоемкость построения активного расписания, допустимого относительно смешанного графа G, не превосходит и, следовательно, общая трудоемкость построения активного расписания, допустимого относительно смешанного графа G, не превосходит 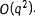
Если для каждого графа G(1)
в алгоритме рассматривать все возможные варианты выбора вершины i, то получим все множество P(G) = {G1
G2
, ..., G} бесконтурных графов, порождаемых смешанным графом G. Следовательно, все множество допустимых относительно G активных расписаний можно построить за 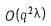 элементарных действий. элементарных действий.
Пример 1.
В условиях примера 3.1 (см. рис. 1) воспользуемся алгоритмом 2 для построения допустимого относительно С = (Q, V, V) расписания.
На этапе 1 алгоритма строим бесконтурный ориентированный граф из множества P{G). Положим G0
= G и выберем на шаг 1 вершину 1, в которую не заходит ни одна дуга. Отметим вершину 1 и заменим дугами инцидентные ей ребра. Получим смешанный граф 
На шаге 2 аналогичные преобразования проделаем для вершины 3, на шаге 3 — для вершины 4, на шаге 4 - для вершины 2, на шаге 5 - для вершины 9. Полученный в результате граф 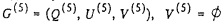 представлен на рис1 в виде сетевого графика. представлен на рис1 в виде сетевого графика.

Рис (2.1)
На этапе 2 воспользуемся алгоритмом 1 для построения активного расписания, допустимого относительно ориентированного графа 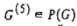 . Сначала сформируем списки потомков и списки предшественников каждой вершины . Сначала сформируем списки потомков и списки предшественников каждой вершины 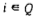 , затем распределим вершины графа , затем распределим вершины графа 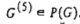 по рангам по рангам  наконец, по формуле 1 вычислим значения наконец, по формуле 1 вычислим значения  для всех вершин для всех вершин  последовательно в порядке неубывания рангов вершин. Полученные значения последовательно в порядке неубывания рангов вершин. Полученные значения  указаны около соответствующих вершин указаны около соответствующих вершин 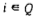 сетевого графика. сетевого графика.
2.1 Последовательный анализ вариантов
Выше рассматривались вопросы построения активного расписания, допустимого относительно ориентированного или смешанного графа. Было Сказано, что не более чем за 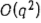 элементарных действий можно построить допустимое расписание либо установить невозможность построения такого расписания. элементарных действий можно построить допустимое расписание либо установить невозможность построения такого расписания.
Если на каждом шаге алгоритма 2 рассматривать все возможные варианты выбора вершины i
, в которую не заходит ни одна исходящая из: неотмеченной вершины дуги, то можно получить все множество P(G={G1
,G2
….G} бесконтурных графов порождаемых графом G = (Q, U, V). Задачу можно решить в результате построения активных расписаний, допустимых относительно графов  ,
и выбора среди них расписания S* минимизирующего значение F
(
s
)-
Трудоемкость полного перебора всех активных расписаний задачи ,
и выбора среди них расписания S* минимизирующего значение F
(
s
)-
Трудоемкость полного перебора всех активных расписаний задачи  может бытьограничена величиной может бытьограничена величиной  при условии, что для вычисления функции F(s) требуется не более при условии, что для вычисления функции F(s) требуется не более  элементарных действий. элементарных действий.
К сожалению, мощность множества P
(
G
)
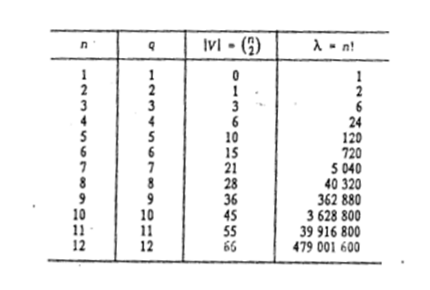
растет в обшей случае экспоненциально с ростом параметров задачи n и М. Например, для задачи  значение значение 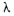 равно n!. Граф
равно n!. Граф  при этом является полным не ориентированным:
при этом является полным не ориентированным: 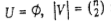 и q
=
n
.
Рост значений |v| и
и q
=
n
.
Рост значений |v| и 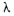 показан в табл. 1
показан в табл. 1
Таблица 1.
Сокращение числа перебираемых расписании можно обеспечить методом последовательного анализа вариантов. Для организации целенаправленного перебора графов множества P(G)будем использовать процедуру последовательного разбиения множества P
(
G
)
на подмножества.
При этом подмножествоP
(
G
)
сначала разбивается va
подмножества P(G1
), P(G2
)…… P(Gk
),
где Gk
,
k
=1,
h- графы, получаемые из 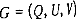 в результате замены одного или нескольких ребер V дугами. Затем одно из множеств P(Gk
),
например P(Gl
),
в свою очередь разбивается на подмножества P(Gh
+1
),
P(Gh
+2
),
..., P(Gh
+
p
),
результате получаем разбиение исходного множества в результате замены одного или нескольких ребер V дугами. Затем одно из множеств P(Gk
),
например P(Gl
),
в свою очередь разбивается на подмножества P(Gh
+1
),
P(Gh
+2
),
..., P(Gh
+
p
),
результате получаем разбиение исходного множества
Этот процесс удобно представлять „растущим" выходящим деревом 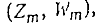 где Zm
- множество его вершина. где Zm
- множество его вершина.
Множество всех конечных вершин дерева (Zm, Wm) будем обозначать через Zm. При выполнении условия а) получаем точное значение f(C'). Нетрудно видеть, что из условия б) следует соотношение 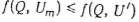 для любого графа для любого графа 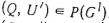 . При выполнении условия в) существует граф . При выполнении условия в) существует граф 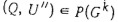 такой, что такой, что 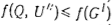 . Следовательно, при поиске оптимального расписания граф G1
можно исключить из рассмотрения, если условие б) или в) выполняется. . Следовательно, при поиске оптимального расписания граф G1
можно исключить из рассмотрения, если условие б) или в) выполняется.
3. Псевдополиномиальное сведение задач и
NP
-трудные в сильном смысле задачи
Наряду с разделением задач на NP-трудные и полиномиально разрешимые, NP-трудные задачи, в свою очередь, подразделяются на NP-трудные в сильном смысле задачи и задачи, имеющие псевдополиномиальные алгоритмы решения.
Алгоритм решения задачи Π называется псевдополиномиальным,
если его временная сложность не превосходит некоторого полинома от двух переменных Lengthn
[
I
]
и M
ax
ц[I]
для любого примера I
задачи Π. Соответствующая задача называется псевдополиномиалъно разрешимой.
Нетрудно заметить, что любой полиномиальный алгоритм является одновременно и псевдополиномиальным.
Кроме того, ни одна из NP-трудных задач, не имеющая числовых параметров, не может иметь псевдополиномиального алгоритма решения, если 
В противном случае такая задача имела бы полиномиальный алгоритм решения, поскольку 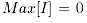 для любого ее примера. Аналогично, если для задачи Π существует такой полином, что для для любого ее примера. Аналогично, если для задачи Π существует такой полином, что для 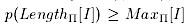 любого любого 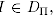 то Π,
удучи NP-трудной, не может быть псевдополиномиально разрешимой.
то Π,
удучи NP-трудной, не может быть псевдополиномиально разрешимой.
Таким образом, существуют NP-трудные задачи, которые не могут иметь даже псевдополиномиальных алгоритмов решения. Такие задачи образуют множество так называемых NP-трудных в сильном смысле задач. Для формализации понятия NP-трудной в сильном смысле задачи введем определение псевдополиномиальной сво димости задач распознавания.
Пусть пары функций (
Lengthn
, M
ax
ц)
и (
Lengthu
', M
ax
ц>)
сопоставлены задачам Π и Π' соответственно.
Говорят, что задача распознавания Π псевдополиномиалъно сводится
к задаче распознавания Π',
если существует словарная функция Φ,
переводящая задачу Π в задачу Π' и удовлетворяющая следующим условиям:
(а) для любого примера 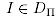 соотношение
соотношение 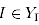 выполняется тогда и только тогда, когда выполняется
выполняется тогда и только тогда, когда выполняется 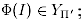
(б) временная сложность вычисления функции Φ не превосходит некоторого полинома q
от двух переменных Lengthn
[
I
]
и Max
п
[
I
] ;
(в) существуют такие полиномы q
iи qi
,
что для любого I

Задача распознавания Π называется NP
-трудной в сильном смысле,
если существует NP-трудная задача распознавания Π,
которая псевдополиномиально сводится к Π и для любого 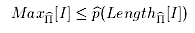
Поскольку любая задача псевдополиномиально сводится к себе, то любая
NP
-трудная задача, удовлетворяющая условию
(1.3), является
NP
-трудной в сильном смысле.
Кроме того, любая NP-трудная в сильном смысле задача является NP-трудной, и ни одна из NP-трудных в сильном смысле задач не может иметь псевдополиномиального алгоритма решения, если 
Понятие псевдполиномиальной сводимости транзитивно. Поэтому для доказательства NP-трудности в сильном смысле некоторой задачи достаточно псевдополиномиально свести к ней некоторую NP-трудную задачу.
Задача распознавания Π называется NP
-полной в сильном смысле,
если Π 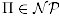 и Π является NP-трудной в сильном смысле. и Π является NP-трудной в сильном смысле.
Экстремальная комбинаторная задача называется NP-трудной в сильном смысле, если сопоставленная ей задача распознавания NP-трудна в сильном смысле.
Примеры
NP
-трудных задач
Ниже приведены формулировки NP-трудных задач, которые в дальнейшем используются при доказательстве NP-трудности задач оптимального планирования.
Разбиение:
Заданы целые положительные числа a
л,
a
о,...,
a
г
и A
такие,


Требуется определить, существует ли множество 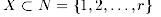 такое что такое что 
4. Использование NP-трудных задач
В настоящее время большое распространение получили криптосистемы с открытыми ключами, характерным свойством которых является то, что знание алгоритма не даёт дополнительных преимуществ при взломе, в отличие от симметричных систем, которые легко взламываются, если знать, по какому базовому правилу они работают. Типичным и самым популярным на данный момент примером системы с открытым ключом является RSA (алгоритм был опубликован в 1977 Ривестом, Шамиром, Эдлманом в MIT). Эта система проста в использовании, и, что более важно, сложна во взломе. Однако до сих пор остаётся открытым вопрос – относится ли задача факторизации, на которой базируется алгоритм RSA, к классу полиномиально разрешимых P или же к классу NP-трудных задач. Задача Р versus NP частично обязана своей значимостью пользующейся успехом теории завершенности NP и частично теории криптографии. Алгоритм удовлетворимости, будучи истинно эффективным алгоритмом по отношению к задаче завершенности NP, с одной стороны, мог бы вызвать к жизни целый ряд полезных алгоритмов для решения многих практических вычислительных задач в промышленности, однако, с другой стороны, такой алгоритм разрушил бы безопасность финансовых и иных сделок, широко использующих Интернет. Не сегодня-завтра может оказаться, что задача факторизации не является NP-трудной и более того, может найтись полиномиальный алгоритм её решения. В этом случае понадобятся совершенно другие методы криптографии. В данной работе я покажу некоторые криптографические методы, основанные на сложности широко известной NP-трудной задачи, задачи о рюкзаке(Knapsack problem)
Заключение
Итак, какой же практический смысл имеет изучение теории сложности и классификация задач с точки зрения NP-полноты? Ответ очевиден — зачастую гораздо разумнее и эффективнее найти доказательство того, что рассматриваемая задача принадлежит к классу NP-полных, и в соответствие с этим заняться поиском достаточно точных приближенных алгоритмов, нежели безрезультатно тратить время на отыскание полиномиальных алгоритмов ее решения. Ясно, что именно NP-полные задачи играют здесь центральную роль — дело в том, что полиномиальное время является, хоть и первым, но достаточно хорошим приближением понятия «практической разрешимости задачи».
Однако существует немало других интересных книг по данной тематике, заслуживающих пристального внимания со стороны читателя. Среди них хотелось бы выделить, где можно найти большое разнообразие NP-полных задач из самых различных областей. Читателям, желающим подробнее ознакомиться с теорией сложности, на мой взгляд, будет интересен подробный курс лекций, глубоко освещающий данную тематику
Библиографический список
1. Гэри М., Джонсон Д. «Вычислительные машины и труднорешаемые задачи» М.: Мир 1982-466 стр.
2. Иванова А.П. «Введение в прикладное программирование. Модели и вычислительные алгоритмы» М.: Физматлит 2002 г.
3. Перепелица В.А. «Асимптотически подход и решение некоторых экстремальных задач на графах. Проблемы кибернетики » М.: Наука, 1973 г.
4. А.В. Яковлев, А.А. Безбогов, В.В. Родин, В.Н.Шамкин, КРИПТОГРАФИЧЕСКАЯЗАЩИТА ИНФОРМАЦИИ
5. Еремеев А.В., Романова А.А., Сервах В.В., Чаухан С.С. Приближенное решение одной задачи управления поставками // Дискретн. анализ и исслед. операций. Серия 2. 2006. Т. 13, № 1. С. 27–39.
|