Министерство образования Республики Беларусь
Учреждение образования
«Брестский государственный университет имени А.С. Пушкина»
Кафедра теоретической физики
КУРСОВАЯ РАБОТА
по физике
Расчет коэффициента ассиметрии при рассеянии релятивистских частиц на кулоновском потенциале
Выполнил
Студент физического факультета
Группы
Научный руководитель
Брест, 2010
Содержание
Введение
1. Дифференциальное сечение
2. Поляризация
3. Случай Кулоновского поля
4. Эксперименты, подтверждающие теорию Мотта
5. Экспериментальная работа Шермана
6. Практическая часть
Заключение
Список используемой литературы
Введение
Объект исследования – электронный пучок, рассеивающийся на мишень.
Цель работы – вычисление коэффициента ассиметрии, функции Шермана и дифференциального сечения при рассеянии релятивистских частиц на кулоновском потенциале.
Рассеяние частиц – изменение направления движения частиц в результате столкновений с другими частицами.
Количественно рассеяние характеризуется эффективным или дифференциальным сечением рассеяния.
Все началось с того, что Резерфорд установил при помощи рассеяния альфа-частиц на золотой фольге строение атома и получил формулу для расчета дифференциального сечения рассеяния в классической релятивисткой механике, которая является функцией от 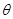 . .
Моттом было показано, что при рассеянии релятивистских неполяризованных электронов происходит частичная поляризация, а при рассеянии частично поляризованных электронов возникает азимутальная асимметрия, т.е. зависимость интенсивности рассеяния частично-поляризованного пучка от угла 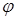 (т.е. при первичном рассеянии неполяризованного пучка происходит его частичная поляризации, а при двойном рассеянии возникает зависимость интенсивности рассеяния частично-поляризованного пучка от (т.е. при первичном рассеянии неполяризованного пучка происходит его частичная поляризации, а при двойном рассеянии возникает зависимость интенсивности рассеяния частично-поляризованного пучка от 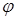 ) [6]. Зависимость интенсивности двойного рассеяния от ) [6]. Зависимость интенсивности двойного рассеяния от 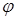 при данных при данных 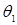 , , 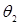 определяется множителем вида 1+ определяется множителем вида 1+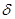 cos cos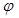 , где данный множитель зависит от , где данный множитель зависит от 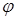 следующим образом. следующим образом.
Эти формулы были получены Моттом [6]. Их особенность заключается в том, что для нахождения численных значений дифференциальных сечений и степени ассиметрии используются не функции, а ряды. Они были получены путем решения уравнений Дирака.
Вонг также получил решение уравнений Дирака, которое отличалось от соотношений, полученных Моттом, значениями коэффициентов Dk
. Вонг пришел к выводу, что асимптотическое аналитическое выражение для сечения рассеяния в приближении малых α
совпадает с аналитическим выражением для сечения Мотта в том же приближении [5,6].
Однако ни Мотт ни Вонг численно суммирования не проводили, а лишь находили различные приближения для рядов [5,6].
Численные подсчеты функции S
(θ)
по формулам Мотта были выполнены Шерманом. Данная функция, называемая функцией Шермана, используется в детекторах Мотта, которые в настоящее время являются основным средством для анализа поляризации электронов.
В данной работе мы рассчитали функцию Шермана по формулам Мотта и сравнили ее с значениями приведенными Шерманом. В ходе этого обнаружилось, что при малых углах и скоростях мы получаем расхождение с Шерманом, а при больших углах наблюдается хорошее согласие.
Также в данной работе мы сравнили экспериментальные значения S
(θ)
при рассеянии электронов золотом с энергиями в диапазоне от 45 до 245 кэВ на угол 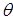 =120 =120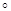 , полученные Спиваком, которые представлены в книге Мотта , со значениями, рассчитанными по Мотту и по Вонгу, и получили, что более близкими к эксперименту являются значения, рассчитанные по Вонгу [5,6].
, полученные Спиваком, которые представлены в книге Мотта , со значениями, рассчитанными по Мотту и по Вонгу, и получили, что более близкими к эксперименту являются значения, рассчитанные по Вонгу [5,6].
Уверенно утверждать, что метод Вонга больше соответствует действительности, мы пока не можем, так как был рассмотрен слишком маленький экспериментальный материал. Проблема требует дальнейших исследований.
1. ДИФФЕРЕНЦИАЛЬНОЕ СЕЧЕНИЕ
Выясним теперь, как должны быть изменены соотношения, полученные для расчета интенсивности рассеяния, когда движение рассматриваемых частиц описывается не уравнением Шредингера, а уравнениями Дирака [6].
Волновая функция 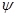 , описывающая рассеяние, имеет теперь четыре компоненты , описывающая рассеяние, имеет теперь четыре компоненты 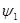 … … обладающие асимптотической формой обладающие асимптотической формой
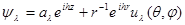 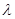 =(1,2,3,4) =(1,2,3,4)
Дифференциальное сечение I(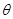 , ,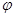 )d )d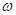 определяется выражением определяется выражением
I(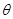 , ,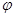 )d )d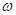 = = d d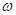
Величины 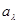 не являются взаимно независимыми. Воспользовавшись решениями (9.12) для плоской волны, находим, что при p1
=p2
=0 и p3
=k не являются взаимно независимыми. Воспользовавшись решениями (9.12) для плоской волны, находим, что при p1
=p2
=0 и p3
=k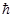
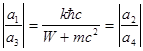
Отсюда независимо от ориентации спина. Аналогичное соотношение существует между значениями 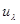 ,так как асимптотически рассеянную волну можно рассматривать как состоящую из ряда плоских волн, распространяющихся из некоторого центра в различных направлениях [6]. Поэтому можно написать ,так как асимптотически рассеянную волну можно рассматривать как состоящую из ряда плоских волн, распространяющихся из некоторого центра в различных направлениях [6]. Поэтому можно написать
I(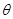 , ,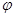 )d )d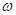 = =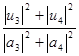 d d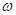
В действительности падающий электронный пучок обычно неполяризован. Такой пучок можно рассматривать как пучок, образованный равным числом электронов с параллельными и с антипараллельными ориентациямп спинов по отношению к направлению распространения. Сначала мы исследуем рассеяние в этих двух частных случаях. Асимптотическая форма функций 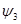 и и  имеет вид имеет вид
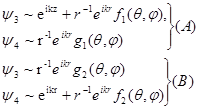
Формулы (А) относятся к электронам со спинами, параллельными направлению падения пучка, а формулы (В) — к электронам со спинами, антипараллельными этому направлению. Для определения функций f
1
,
f
2
,
g
1
,
g
2
можно воспользоваться решениями уравнений (9.10), найденными Дарвином для того случая, когда скалярный потенциал V зависит только от r
, а векторный потенциал равен нулю. Дарвин получил следующие группы решений:
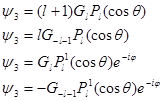 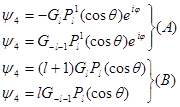
где 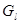 является решением системы уравнений является решением системы уравнений
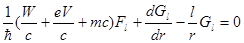
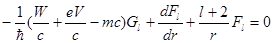
AG-
l
-1
решение аналогичной пары уравнений, получаемой путем замены lна –l-1.
Исключая функцию Fl
находим
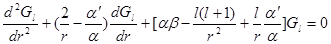
Где
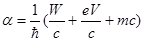 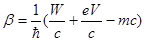 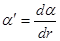
Подстановка
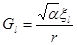
приводит к уравнению, имеющему вид уравнения Шредингера [см. формулу (2.12)]
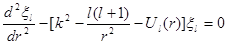
Где
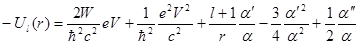
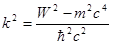
Аналогичный результат получается также и для функции  при замене l
на -l-1. при замене l
на -l-1.
Первые два члена выражения (9.23), определяющего Ul
(r), не зависят от спина электрона и являются типичными для уравнения Клейна-Гордона, описывающего бесспиновую частицу. Остальные члены связаны со спин-орбитальным взаимодействием и зависят не только от потенциала, но также и от силы и ее радиальной производной.
Отсюда следует, что собственные решения 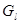 ,G
-
l
-1
уравнений (9.20) имеют асимптотический вид ,G
-
l
-1
уравнений (9.20) имеют асимптотический вид
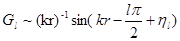
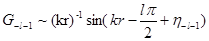
так как значение l(l+1) остается неизменным при замене l
на –
l
-1
.
С помощью решений (9.19) (А) можно получить функции 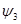 , ,  , имеющие асимптотическую форму (9.18) (А): , имеющие асимптотическую форму (9.18) (А):
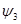 = =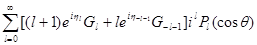
 = =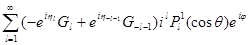
Это дает
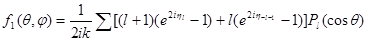
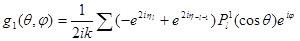
Сопоставляя полученные формулы с выражением (2.1), легко убедиться в том, что не релятивистский случай соответствует условию 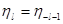 . .
В случае антипараллельных спинов [решения (В)] аналогичным образом находим
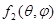 = =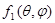 = =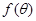
И
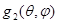 = =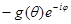
Где
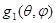 = =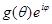
В общем случае произвольного исходного направления спинов, когда падающая волна описывается функциями
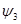 =
Aeikz =
Aeikz
 =
Beikz =
Beikz
линейная комбинация найденных выше решений дает
u3
=Af-Bge-i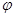
u4
=Bf+Age-i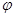
так что
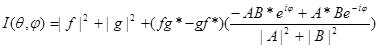
2. ПОЛЯРИЗАЦИЯ
Из выражения (9.28) следует, что рассеяние частично поляризованного пучка зависит не только от угла 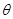 , но также и от угла , но также и от угла 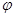 . Так, и в случае, соответствующем изображенному на рис. 37, интенсивность рассеяния в направлении СО будет отлична от интенсивности рассеяния в направлении СЕ. Эффект такого рода можно было бы обнаружить путем исследования двойного рассеяния электронного пучка. Пусть неполяризованный пучок электроном падает на мишень В. Электроны, рассеянные в направлении ВС, попадаю; . Так, и в случае, соответствующем изображенному на рис. 37, интенсивность рассеяния в направлении СО будет отлична от интенсивности рассеяния в направлении СЕ. Эффект такого рода можно было бы обнаружить путем исследования двойного рассеяния электронного пучка. Пусть неполяризованный пучок электроном падает на мишень В. Электроны, рассеянные в направлении ВС, попадаю;

затем на мишень С. Этот рассеянный пучок частично поляризован в результате рассеяния на мишени В, так как рассеивающее поле оказывает различное влияние па электроны с параллельными и антипараллельными спинами. Электронные пучки, испытавшие вторичное рассеяние в направлениях СDч СЕ под одним и тем же углом 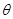 2
по отношению к направлению ВС, будут, следовательно, обладать различной интенсивностью. 2
по отношению к направлению ВС, будут, следовательно, обладать различной интенсивностью.
Подробная теория такого двойного рассеяния впервые была разработана Моттом [11]. Падающий неполяризованный пучок мы, как всегда, будем считать состоящим из равного количества электронов со спинами, параллельными и антипараллельными направлению падения пучка [6].
Для электронов падающего пучка, обладающих антипараллельными спинами,
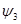 =
Aeikz
, =
Aeikz
,
 =0, AA*= =0, AA*=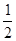
После первичного рассеяния на угол 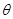 1
, в плоскости 1
, в плоскости 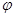 = 0 (плоскость AВС на рис. 37) компоненты волновой функции будут пропорциональны = 0 (плоскость AВС на рис. 37) компоненты волновой функции будут пропорциональны 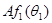 и и 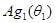 . Повернем теперь координатные оси на угол . Повернем теперь координатные оси на угол 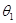 таким образом, чтобы ось z была направлена вдоль ВС, а плоскость АBС осталась плоскостью таким образом, чтобы ось z была направлена вдоль ВС, а плоскость АBС осталась плоскостью 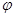 =0. В этойновой системе координат =0. В этойновой системе координат
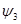 = =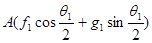  = =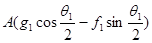
(член еikz
и постоянный множитель здесь опущены). Подставляя эти функции в выражение (9.28) вместо А и В, получаем интенсивность |
u
3
|2
+|
u
4
|2
вторичного рассеяния. Вычисления производятся точно таким же образом и тогда, когда электроны падающего пучка обладают спинами, параллельными направлению падения. Складывая полученные значения интенсивности,находим интенсивность рассеяния в направлении (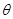 2
, 2
, 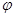 2
) 2
)
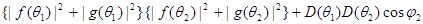
Где
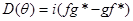
Из этой формулы видно, что при данных значениях 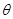 1
и 1
и 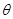 2
зависимость интенсивности рассеяния от угла 2
зависимость интенсивности рассеяния от угла 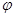 2
определяется множителемвида 2
определяется множителемвида
1+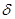 cos cos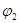
где
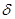 = =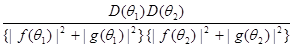
Зависимость этого множителя от угла 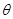 имеет следующий вид при каком-то фиксированном значении имеет следующий вид при каком-то фиксированном значении 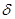 : :
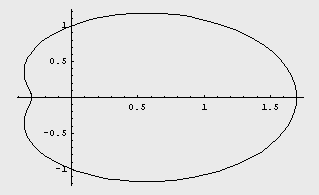
При 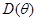 =0 рассматриваемый эффект исчезает. В этом случае рассеяние приводит к повороту всех первоначальных направлений спина на один и тот же угол, так что неполяризованный пучок остается неполяризованным. =0 рассматриваемый эффект исчезает. В этом случае рассеяние приводит к повороту всех первоначальных направлений спина на один и тот же угол, так что неполяризованный пучок остается неполяризованным.
В общем случае при малых значениях 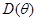 степень асимметрии будет мала, хотя она может принимать большие значения при некоторых специальных условиях, когда знаменатель выражения (9.31) очень мал. Множитель степень асимметрии будет мала, хотя она может принимать большие значения при некоторых специальных условиях, когда знаменатель выражения (9.31) очень мал. Множитель 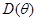 , вообще говоря, мал тогда, когда мала величина g
, т. е. в нерелятивистском случае. Возвращаясь к формулам (9.26) и (9.27), мы видим, что , вообще говоря, мал тогда, когда мала величина g
, т. е. в нерелятивистском случае. Возвращаясь к формулам (9.26) и (9.27), мы видим, что
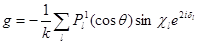
Где
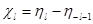 , , 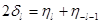
Фазы 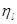 и и 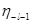 могут быть вычислены с помощью уравнения (9.22) для функции могут быть вычислены с помощью уравнения (9.22) для функции 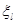 и соответствующего уравнения для функции и соответствующего уравнения для функции  . Выражения, определяющие эти фазы, отличаются друг от друга только одним членом, пропорциональным . Выражения, определяющие эти фазы, отличаются друг от друга только одним членом, пропорциональным 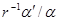 ; в случае функции ; в случае функции 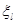 этот член содержит множитель l
+1
, в случае функции этот член содержит множитель l
+1
, в случае функции  — множитель -
l
. Поскольку величина — множитель -
l
. Поскольку величина 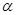 ' пропорциональна dV/dr, то разность фаз ' пропорциональна dV/dr, то разность фаз 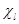 , а следовательно, функция , а следовательно, функция 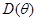 и степень асимметрии электронного пучка определяются не потенциалом рассеивающего поля, а величиной рассеивающей силы [6]. и степень асимметрии электронного пучка определяются не потенциалом рассеивающего поля, а величиной рассеивающей силы [6].
3. СЛУЧАИ КУЛОНОВСКОГО ПОЛЯ
Рассмотрим теперь рассеяние быстрых электронов неэкранированным атомным ядром с зарядом Z
е
, когда
V
=-
Ze
/
r
Как и в нерелятивистском случае, исследованном в гл. 3, медленное убывание этого потенциала с расстоянием вызывает изменение асимптотической формы функций 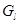 и и 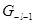 . Формулы (9.26) и (9.27) остаются справедливыми, а фазы . Формулы (9.26) и (9.27) остаются справедливыми, а фазы 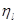 и и 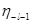 таковы, что таковы, что
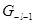 ~ ~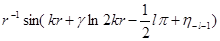
Где 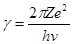
Уравнения (9.20), определяющие функции 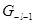 , приобретают теперь вид , приобретают теперь вид
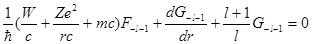
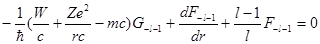
Записывая
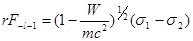
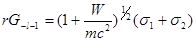
Имеем
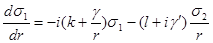
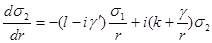
Где 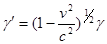 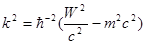
Разлагая 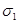 и и 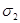 в ряд в ряд
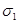 = =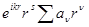 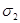 = =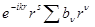
Находим, что регулярные решения могут быть представлены в виде
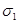 = =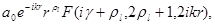
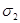 = =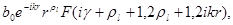
Где
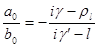 , , 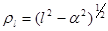 , , 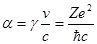
Это дает
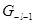 = =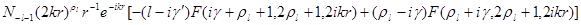
Где 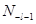 - постоянная. Воспользовавшись асимптотическими значениями гипергеометрических функций, приведенных в гл. 3, § 3, имеем - постоянная. Воспользовавшись асимптотическими значениями гипергеометрических функций, приведенных в гл. 3, § 3, имеем
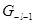 ~ ~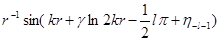
Где 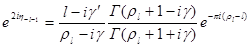
Постоянная 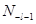 равна, таким образом, равна, таким образом,
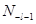 = =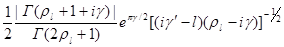
Записывая
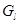 = =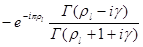
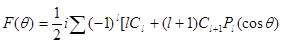
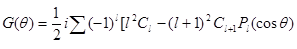
И подставляя (9.42) и соответствующее выражение для ехр(2
i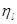 )
в формулы (9.26) и (9.27), получаем
)
в формулы (9.26) и (9.27), получаем
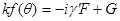
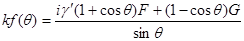
Следовательно, дифференциальное сечение равно
|
f
|2+|
g
|2
=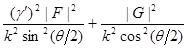
Функции F и G не могут быть получены в конечной форме; при рассеянии легкими элементами они могут быть,однако, разложены в ряд по степеням 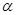 , поскольку , поскольку 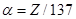 . .
В предельном случае 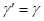 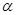 2
=0
справедливы результаты, полученные нами при исследовании рассеяния кулоновским полем без учета спинового и релятивистского эффектов. Из формулы (3.16) следует, что в этом случае 2
=0
справедливы результаты, полученные нами при исследовании рассеяния кулоновским полем без учета спинового и релятивистского эффектов. Из формулы (3.16) следует, что в этом случае
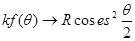 g
( g
(
 ) )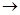 0 0
Где R
=
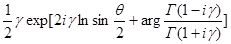
Разлагая F и G в ряд по степеням 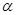 , имеем , имеем
F
=
F
0
+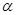 F
1
+
F
1
+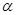 2
F
2
+… 2
F
2
+…
G
=
G
0
+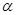 G
1
+
G
1
+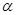 2
G
2
+… 2
G
2
+…
Воспользовавшись формулой (9.45) при 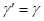 , получаем , получаем
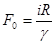 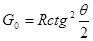
ПосколькуF
иGдолжны зависеть от 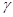 , подставляемэти функции в (9.46) и находим дифференциальное сечение , подставляемэти функции в (9.46) и находим дифференциальное сечение
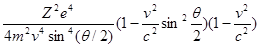
Эта формула справедлива для всех значений v
при условии, что величина 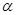 мала по сравнению с единицей. мала по сравнению с единицей.
Следовательно, в рассматриваемом приближении формула Резерфорда должна быть умножена на выражение
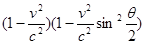
Первый множитель учитывает лоренцево сжатие, второй связан с наличием спина. Поскольку в этом приближении как f, так и g вещественны (если опустить общий фазовый множитель 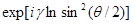 ), то при двойном рассеянии не должно было бы наблюдаться никакой асимметрии. Для получения конечного значения величины ), то при двойном рассеянии не должно было бы наблюдаться никакой асимметрии. Для получения конечного значения величины 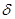 , определяемой формулой (9.31), необходимо решить задачу в следующем приближении. Это было проделано Моттом [11], который показал, что при , определяемой формулой (9.31), необходимо решить задачу в следующем приближении. Это было проделано Моттом [11], который показал, что при 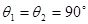
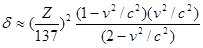
При v
/
c
=0,81
эта функция приобретает минимальное значение, равное 0,2(Z/137)2
. Дифференциальное сечение (9.17), вычисленное в том же приближении, содержит множитель [13,14]
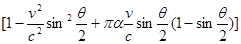
Вместо множителя
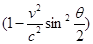
В случае рассеяния тяжелыми элементами отношение Z/137уже не является малым, и приближенные формулы (9.47),(9.48) перестают быть справедливыми. Мотт впервые определил численные значения дифференциальных сечений и степени асимметрии с помощью точных формул (9.45). В 1932 г. он вычислил
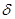 как функцию отношения v
/с
для случая двукратного рассеяния на 90° электронов ядрами золота и нашел также значения дифференциальных сечений для однократного рассеяния электронов на этот угол.
как функцию отношения v
/с
для случая двукратного рассеяния на 90° электронов ядрами золота и нашел также значения дифференциальных сечений для однократного рассеяния электронов на этот угол.
С тех пор было проведено много дальнейших расчетов; в настоящее время имеются таблицы дифференциальных сечений для рассеяния электронов ядерными кулоновскими полями в широком интервале значений углов и энергии. Так, например, Доггет и Спенсер [15] протабулировали значения 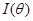 через каждые 15° для рассеяния электронов с энергиями 10; 4; 2; 1; 0,7; 0,4; 0,2; 0,1 и 0,05 МэВ точечными зарядами Zeпри Z=6; 13; 29; 50; 82 и 92. Шерман [16] составил таблицы для Z= 13, 18 и 80 с интервалом 15° для рассеяния электронов при значениях через каждые 15° для рассеяния электронов с энергиями 10; 4; 2; 1; 0,7; 0,4; 0,2; 0,1 и 0,05 МэВ точечными зарядами Zeпри Z=6; 13; 29; 50; 82 и 92. Шерман [16] составил таблицы для Z= 13, 18 и 80 с интервалом 15° для рассеяния электронов при значениях 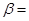 0,2; 0,4; 0,5; 0,6; 0,7; 0,8 и 0.9. Полученные им таблицы содержат не только 0,2; 0,4; 0,5; 0,6; 0,7; 0,8 и 0.9. Полученные им таблицы содержат не только 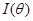 , но также и значеиия функций F
и G, входящих в формулы (9.45), и параметра асимметрии , но также и значеиия функций F
и G, входящих в формулы (9.45), и параметра асимметрии 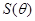 , определяемого выражением , определяемого выражением
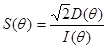
Фактически 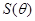 дает величину поляризации Ри
,вызванной рассеянием падающего неполяризованного пучка на угол дает величину поляризации Ри
,вызванной рассеянием падающего неполяризованного пучка на угол  . .
Параметр ассиметрии еще называют функцией Шермана, так как этот параметр был числено подсчитан Шерманом.
Параметр 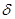 , определяемый формулой (9.31), равен , определяемый формулой (9.31), равен
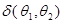 =S( =S(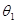 )S( )S(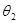 ) )
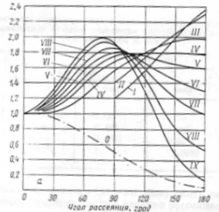
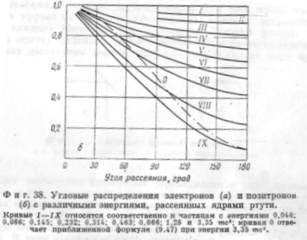
Рис. 38 иллюстрирует зависимость сечений однократного рассеяния от угла и энергии для рассеяния ртутью (Z=80). По оси ординат отложено отношение r
найденной интенсивности рассеяния к интенсивности рассеяния, определяемой формулой Резерфорда
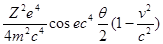 , ,
Учитывающей зависимость массы от скорости. В случае тяжелых элементов приближенное значение r
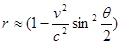 , ,
фигурирующее в формуле (9.47), становится очень неточным.
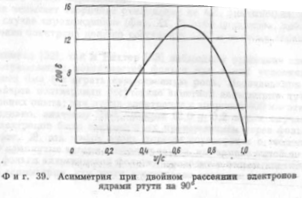
Зависимость степени асимметрии 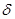 от скорости электронов при от скорости электронов при 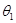 = =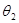 =90° иллюстрируется на рис. 39. Из графика следует, что эффект асимметрии при двойном рассеянии должен приобретать существенную роль при значениях v
/с
, близких к 0,6. Хотя эти результаты были получены в предположении, что рассеяние электронов обусловлено «голыми» ядрами, в дальнейшем было показано [17—19], что эффект экранирования ядра атомными электронами не должен оказывать существенного влияния на значения =90° иллюстрируется на рис. 39. Из графика следует, что эффект асимметрии при двойном рассеянии должен приобретать существенную роль при значениях v
/с
, близких к 0,6. Хотя эти результаты были получены в предположении, что рассеяние электронов обусловлено «голыми» ядрами, в дальнейшем было показано [17—19], что эффект экранирования ядра атомными электронами не должен оказывать существенного влияния на значения 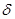 , предсказываемые теорией. , предсказываемые теорией.

Рис. 40. Зависимость степени асимметрии 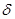 от угла рассеяния (
от угла рассеяния (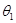 = =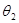 = = ) при
) при 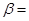 0,6.
0,6.
На рис. 40 представлена зависимость 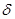 от угла рассеяния при от угла рассеяния при 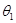 = =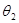 . Как видно, при . Как видно, при 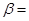 0,6 величина 0,6 величина 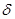 имеет максимум при 120°. Это определяет условия максимально возможной асимметрии для всех возможных углов и энергий. имеет максимум при 120°. Это определяет условия максимально возможной асимметрии для всех возможных углов и энергий.
4. ЭКСПЕРИМЕНТЫ, ПОДТВЕРЖДАЮЩИЕ ТЕОРИЮ
Хотя первые эксперименты по проверке предсказаний теории рассеяния быстрых электронов, принадлежащей Мотту, находились в резком противоречии с ней, теперь очевидно, что эта теория хорошо согласуется с результатами наблюдений. Следует, однако, учитывать, что мы имеем дело со столкновениями электронов с ядрами при таких энергиях, когда структура ядра не должна влиять на результаты опытов.
Результаты наблюдений, проведенных до 1942 г., обзор которых сделан в работе Урбана [20], дают очень нечеткую картину. Однако вскоре после воины, Ван дер Грааф и сотр. [21, 22] выполнили эксперименты с электронами в области энергий от 1,27 до 2,27 Мэв и углов рассеяния от 20 до 50°, обнаружившие хорошее согласие с теорией.
Опыты в более широком диапазоне углов проводились Байярдом и Интема [23] также с использованием генератора Ван дер Граафа. В табл. 9.1 приведены некоторые из полученных ими результатов, относящиеся к рассеянию электронов с энергией 1 Мэв на алюминии и золоте, которые сравниваются с вычисленными значениями. Как видно из таблицы, согласие является очень хорошим, так что нет основания сомневаться в справедливости теории для рассматриваемого интервала энергий.
Сравнение теоретических и экспериментальных значений дифференциального сечения рассеяния электронов с энергией 1 Мэв на алюминии и золоте
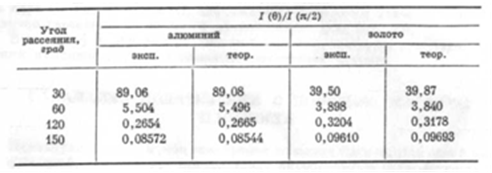
Был предпринят ряд попыток обнаружить на опыте предсказываемый теорией эффект асимметрии при двойном рассеянии электронов ядрами золота. Вплоть до появления работы Шелла, Чейза и Майерса [35] эти попытки оставались, однако, безуспешными. Для того чтобы можно было обнаружить эффект асимметрии, существенно, конечно, устранить деполяризующее влияние многократного рассеяния. Золотая фольга, использовавшаяся в опытах Даймонда [32] и Рихтера [33] в качестве источника рассеяния, была достаточно тонкой, для того чтобы можно было пренебречь многократным рассеянием электронов, приводящим к ряду отклонений на малые углы; однако вероятность отклонения на 90° в результате двух последовательных отклонений сравнимой величины, по-видимому, не была при этом достаточно малой.

Отклонение на 90° становится заметным [36—38] только тогда, когда электроны рассеиваются «отражающей» стороной фольги (рис. 41, а). В этом случае электрон, испытавший отклонение на 45°, движется в фольге почти параллельно ее слою, и, следовательно, вероятность того, что он испытает вторичное отклонение на 45°, значительна. С другой стороны, в случае «прохождения» (фиг. 41, б) либо первичное, либо вторичное отклонение электрона должно составлять 135° и поэтому гораздо менее вероятно.
Как Даймонд [32], так и Рихтер [33] наблюдали рассеяние электронов на 90° от отражающих поверхностей фольги при таких условиях, когда эффект должен был бы играть существенную роль. Исследования Шелла, Чейза и Майерса подтвердили отсутствие заметной асимметрии при аналогичных условиях опыта; для пучка электронов с энергией 400 кэвэти авторы получили, однако, значение 200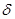 , равное 12,0 ± 0,2 в том случае, когда рассеяние электронов было связано с их прохождением через фольгу. Как следует из рис. 39, эта цифра очень хорошо согласуется с теоретическим значением. Упомянутые авторы показали также, что замена одной из пластинок золотой фольги алюминиевой фольгой приводит к весьма значительному уменьшению асимметрии, как этого и следовало ожидать. , равное 12,0 ± 0,2 в том случае, когда рассеяние электронов было связано с их прохождением через фольгу. Как следует из рис. 39, эта цифра очень хорошо согласуется с теоретическим значением. Упомянутые авторы показали также, что замена одной из пластинок золотой фольги алюминиевой фольгой приводит к весьма значительному уменьшению асимметрии, как этого и следовало ожидать.
Наиболее точные измерения коэффициента асимметрии сейчас принадлежат Спиваку и др. [39]. Они измеряли асимметрию при рассеянии электронов с энергиями от 45 до 245 кэв, золотом при углах 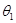 = =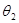 =120°. Сравнение между теорией и опытом проведено в табл. 9.2. =120°. Сравнение между теорией и опытом проведено в табл. 9.2.
Сравнение экспериментальных и теоретических значений параметра асимметрии 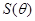 для двойного рассеяния электронов золотом на угол 120° для двойного рассеяния электронов золотом на угол 120°
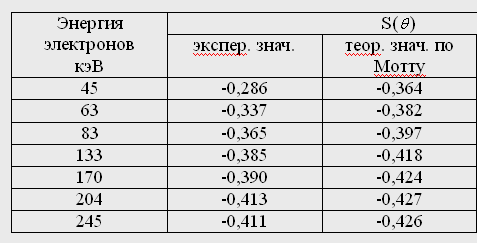
Согласие можно считать хорошим, особенно в случае высоких энергий. Некоторое несоответствие, увеличивающееся с уменьшением энергии, возможно, отчасти связано с тем, что при вычислениях трудно учесть экранирование.
В качестве других опытов, которые очень хорошо согласуются с теорией, следует упомянуть наблюдения, проведенные Петтусом [40] и Нельсоном и Пиддом [41].
5.ЭКСПЕРИМЕНАЛЬНАЯ РАБОТА ШЕРМАНА
Теория электронов Дирака была применена Moттом к рассеянию электронов ядрами, чтобы исследовать возможные эффекты поляризации в двойных экспериментах рассеяния. Теоретические результаты для ожидаемой поляризации и для дифференциальных поперечных сечений рассеяния медленно вовлекают в условно сходящиеся ряды, которые не поддаются легкому вычислению. Moтт вычислил результаты для золота (Z=79) в 90 градусах. Барлет и Ватсон суммировали ряд в цифровой форме для ртутных ядер (Z=80) по диапазону углов и энергий. Позже, другие исследователи выполнили числовые вычисления. В работе Шермана ряд Moтта, поляризация, и дифференциальное поперечное сечение рассеяния оценены для рассеяния электронов ядрами заряда Z=80, 48, и 13, в энергиях, данных отношением электронной скорости, чтобы осветить скорость, 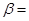 v
/
c
=
0.2,
0.4, 0.5, 0.6, 0.7, 0.8, и 0.9, через рассеивание углов, v
/
c
=
0.2,
0.4, 0.5, 0.6, 0.7, 0.8, и 0.9, через рассеивание углов,  , в интервалах с 15 градусов от 15 градусов до 165. Эти вычисления были выполнены при помощи компьютера UNIVAC. [3] , в интервалах с 15 градусов от 15 градусов до 165. Эти вычисления были выполнены при помощи компьютера UNIVAC. [3]
Формулы, которыми пользовался в своих расчетах Шерман, имеют следующий вид:
Отличительное поперечное сечение для неполяризованного луча электронов, рассеянных через угол  , ,
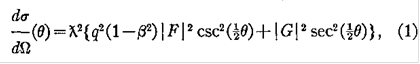
Где 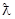 является длина волны де Бройля, является длина волны де Бройля, 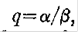
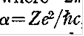 , и , и 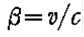 . Если неполяризованный луч будет рассеян через угол . Если неполяризованный луч будет рассеян через угол 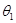 ,,
то рассеянные электроны будут частично поляризованы. Если этот частично поляризованный луч будет рассеян снова через угол ,,
то рассеянные электроны будут частично поляризованы. Если этот частично поляризованный луч будет рассеян снова через угол 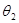 , то интенсивность дважды рассеянных электронов будет тогда зависеть от азимута в направлении , то интенсивность дважды рассеянных электронов будет тогда зависеть от азимута в направлении 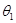 .
Дифференциальное поперечное сечение для этого двойного рассеивающегося процесса .
Дифференциальное поперечное сечение для этого двойного рассеивающегося процесса
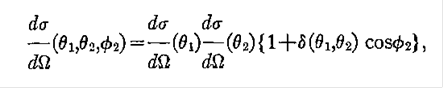
где 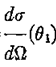 и и 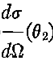 определены (1), определены (1), 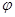 2,
являюсь азимутальным углом в направлении 2,
являюсь азимутальным углом в направлении 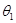 и и 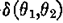 асимметрия поляризации.
асимметрия поляризации.
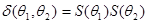
Где
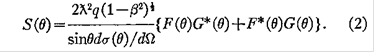
где Г- гамма функция, и 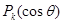 - полиномы Лежандра порядка k
.
Dk
дают - полиномы Лежандра порядка k
.
Dk
дают
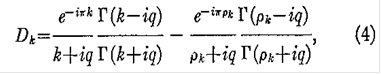
где 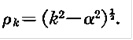
Отношения гамма функций, которые появляются в формуле (4) были оценены при использовании отношений рекурсии для гамма функций и приближения Стерлинга следующим образом:


В последнем уравнении x
обращается или к k
или к pk
в формуле (4). [Отношение гамма функции, которое появляется на определении Fo
,
может быть записано
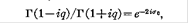
где 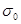 доступен в изданных таблицах ] доступен в изданных таблицах ]
С этими приближениями были оценены Dk
. Эти условия были вставлены в (3) и ряд, Fi
и Gi
были определены в численной форме. Так как эти ряды являются условно сходящимися и сходятся очень медленно, использовались два преобразования. Сначала "сокращенный" ряд Yennie, Ravenhall, и Wilson8
использовался, чтобы улучшить конвергенцию под маленькими углами. Это преобразование может быть применено к любому ряду полиномов Лежандра, данных
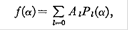
где 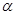 =cos =cos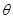 . С использованием отношений повторения для полиномов Лежандра этот ряд может быть преобразован к . С использованием отношений повторения для полиномов Лежандра этот ряд может быть преобразован к
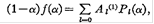
или
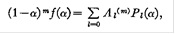
Где

Ряды для F
1
и G
1
были "сокращены" в этой манере с m=3.
Второе преобразование было применено к сокращенному ряду. Это - известное преобразование Эйлера, которое является соответствующим для этих рядов. Это преобразование дано
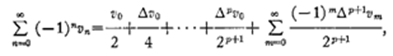
Где
 [3] [3] |
Данные полученные Шерманом
Z
=80
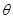 ° ° |
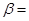 0.2 0.2 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
| 15 |

S
|
2.64*108
2.11*10-3
|
1.47*107
-4.25*10-4
|
5.35*106
1.60*10-3
|
2.21*106
3.45*10-3
|
9.67*105
4.04*10-3
|
4.10*105
3.77*10-3
|
1.39*105
2.79*10-3
|
| 30 |

S
|
1.72*107
-1.93*10-3
|
9.3*105
1.53*10-2
|
3.48*105
1.96*10-2
|
1.51*105
1.66*10-2
|
6.89*104
1.14*10-2
|
3.03*104
6.32*10-3
|
1.06*104
2.3*10-3
|
| 45 |

S
|
3.63*106
-9.65*10-3
|
1.99*105
3.93*10-2
|
7.93*104
2.01*10-2
|
3.59*104
2.02*10-3
|
1.68*104
-1.06*10-2
|
7.53*103
-1.74*10-2
|
2.66*103
-1.76*10-2
|
| 60 |

S
|
1.19*106
5.64*10-2
|
7.45*104
2.18*10-3
|
3.09*104
-3.8*10-2
|
1.42*104
-6.16*10-2
|
6.69*103
-7.22*10-2
|
2.99*103
-7.1*10-2
|
1.05*103
-5.86*10-2
|
| 75 |

S
|
5.21*105
8.3*10-2
|
3.81*104
-0.104
|
1.59*104
-0.143
|
7.25*103
-0.160
|
3.37*103
-0.162
|
1.48*103
-0.150
|
5.11*102
-0.117
|
| 90 |

S
|
2.94*105
-3.59*10-2
|
2.35*104
-0.234
|
9.64*103
-0.261
|
4.29*103
-0.271
|
1.94*103
-0.265
|
8.3*102
-0.242
|
2.78*102
-0.190
|
| 105 |

S
|
2.1*105
-0.203
|
1.66*104
-0.333
|
6.56*103
-0.356
|
2.81*103
-0.367
|
1.22*103
-0.364
|
5.01*102
-0.34
|
1.6*102
0.277
|
| 120 |

S
|
1.8*105
-0.283
|
1.29*104
-0.372
|
4.89*103
-0.401
|
2.00*103
-0.424
|
8.27*102
-0.436
|
3.19*102
-0.429
|
94.4
-0.373
|
| 135 |

S
|
1.71*105
-0.262
|
1.1*104
-0.342
|
3.95*103
-0.380
|
1.54*103
-0.418
|
5.98*102
-0.453
|
2.13*102
-0.479
|
56.3
-0.464
|
| 150 |

S
|
1.69*105
-0.188
|
9.86*103
-0.257
|
3.42*103
-0.295
|
1.27*103
-0.337
|
4.66*102
-0.387
|
1.52*102
-0.446
|
34.2
-0.505
|
| 165 |

S
|
1.69*105
-9.56*10-2
|
9.31*103
-0.137
|
3.15*103
-0.161
|
1.13*103
-0.189
|
3.97*102
-0.226
|
1.20*103
-0.281
|
22.6
-0.380
|
Z
=
4
8
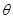 ° ° |
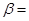 0.2 0.2 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
| 15 |

S
|
9.51*107
-1.14*10-4
|
5.25*106
1.81*10-3
|
1.95*106
1.64*10-3
|
8.19*105
1.22*10-3
|
3.58*105
7.56*10-4
|
1.51*105
3.58*10-4
|
5.03*104
7.35*10-5
|
| 30 |

S
|
6.12*106
4.37 *10-3
|
3.54*105
2.30*10-3
|
1.34*105
-1.16*10-3
|
5.68*104
-3.67*10-3
|
2.50*104
-5.23*10-3
|
1.06*104
-5.81*10-3
|
3.55*103
-5.13*10-3
|
| 45 |

S
|
1.28*106
0.0123
|
7.78*104
-0.0119
|
2.96*104
-0.0188
|
1.26*104
-0.0227
|
5.52*103
-0.0242
|
2.33*103
-0.0232
|
776
-0.0188
|
| 60 |

S
|
4.50*105
7.70*10-4
|
2.78*104
-0.0427
|
1.05*104
-0.0510
|
4.43*103
-0.0550
|
1.93*103
-0.0554
|
803
-0.0515
|
264
-0.0410
|
| 75 |

S
|
2.12*105
-0.0372
|
1.30*104
-0.0832
|
4.86*103
-0.0919
|
2.01*103
-0.0959
|
862
-0.0953
|
352
-0.0886
|
113
-0. 0710
|
| 90 |

S
|
1.21*105
-0.080
|
7.23*103
-0.123
|
2.56*103
-0.133
|
1.08*103
-0.139
|
0449
-0.139
|
178
-0.131
|
55.5
-0.108
|
| 105 |

S
|
7.99*104
-0.112
|
4.58*103
-0.153
|
1.64*103
-0.166
|
646
-0.175
|
261
-0.180
|
99.6
-0.176
|
29.5
-0.151
|
| 120 |

S
|
5.91*104
-0.122
|
3.22*103
-0.163
|
1.12*103
-0.180
|
428
-0.195
|
166
-0.208
|
60.1
-0.213
|
16.5
-0.197
|
| 135 |

S
|
4.77*104
-0.110
|
2.48*103
-0.151
|
840
-0.170
|
310
-0.190
|
115
-0.211
|
39.0
-0.231
|
9.60
-0.238
|
| 150 |

S
|
4.15*104
-0.0822
|
2.07*103
-0.116
|
684
-0.134
|
245
-0.153
|
87.2
-0.177
|
27.4
-0.208
|
5.87
-0.247
|
| 165 |

S
|
3.83*104
-0.0435
|
1.85*103
-0.0630
|
606
-0.0736
|
212
-0.0863
|
73.1
-0.103
|
21.7
-0.128
|
4.00
-0.176
|
Z= 13
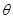 ° ° |
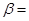 0.2 0.2 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
| 15 |

S
|
6.98*106
2.97 *10-5
|
3.84*105
-1.92*10-4
|
1.41*105
-2.68*10-4
|
5.80*104
-3.24*10-4
|
2.50*104
-3.56*10-4
|
1.04*104
-3.55*10-4
|
3.41*103
-2.94*10-4
|
| 30 |

S
|
4.54*105
-7.90*10-4
|
2.50*104
-1.80*10-3
|
9.13*103
-2.13*10-3
|
3.75*104
-2.36*10-3
|
1.61*103
-2.45*10-3
|
6.63*102
-2.35*10-3
|
2.17*102
-1.92*10-3
|
| 45 |

S
|
9.52*104
-3.00*10-3
|
5.20*103
-5.14*10-3
|
1.89*103
-5.88*10-3
|
7.72*102
-6.40*10-3
|
3.28*102
-6.60*10-3
|
1.34*102
-6.33*10-3
|
43.3
-5.19*10-3
|
| 60 |

S
|
3.27*104
-6.28*10-3
|
1.76*103
-9.73*10-3
|
6.35*102
-0.0110
|
2.56*102
-0.0120
|
1.07*102
-0.0125
|
43.0
-0.0121
|
13.6
-0.0101
|
| 75 |

S
|
1.48*104
-9.90*10-3
|
7.87*102
-0.0147
|
2.80*102
-0.0167
|
1.11*102
-0.0184
|
45.7
-0.0194
|
17.9
-0.0192
|
5.50
-0.0164
|
| 90 |

S
|
8.11*103
-0.0130
|
4.22*102
-0.0191
|
1.48*102
-0.0220
|
57.7
-0.0244
|
23.1
-0.0263
|
8.76
-0.0269
|
2.58
-0.0240
|
| 105 |

S
|
5.09*103
-0.0150
|
2.60*102
-0.0220
|
89.6
-0.0256
|
34.2
-0.0290
|
13.3
-0.0321
|
4.83
-0.0341
|
1.34
-0.0324
|
| 120 |

S
|
3.56
-0.0152
|
1.78
-0.0226
|
6.04
-0.0266
|
2.25
-0.0309
|
8.47
-0.0353
|
2.93
-0.0394
|
0.748
-0.0406
|
| 135 |

S
|
2.74*103
-0.0136
|
1.34*102
-0.0205
|
44.8
-0.0244
|
16.3
-0.0290
|
5.94
-0.0342
|
1.94
-0.0404
|
0.446
-0.0461
|
| 150 |

S
|
2.28*103
-0.0102
|
1.10*102
-0.0155
|
36.4
-0.0187
|
13.0
-0.0226
|
4.58
-0.0276
|
1.42
-0.0343
|
0.288
-0.0444
|
| 165 |

S
|
2.05*103
-5.48*10-3
|
98.0
-8.38*10-3
|
32.1
-0.0102
|
11.3
-0.0125
|
3.90
-0.0156
|
1.16
-0.0202
|
0.211
-0.0290
|
[3].
В данной работе мы рассчитали функцию Шермана S
(θ)
по формулам Мотта и сравнили ее с значениями приведенными Шерманом [3]. В ходе этого обнаружилось, что при малых углах и скоростях мы получаем расхождение с Шерманом, а при больших углах наблюдается хорошее согласие.
Z=80
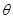 ° ° |
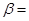 0.2 0.2 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
| 15 |
S |
-0.000418302 |
-0.000756439 |
0.00145307 |
0.00329674 |
0.0039953 |
0.00373716 |
0.00274968 |
| 30 |
S |
-0.00187486 |
0.0152943 |
0.0195888 |
0.0166319 |
0.0114146 |
0.0063109 |
0.00229958 |
| 45 |
S |
-0.0096423 |
0.0392795 |
0.0201246 |
0.00200746 |
-0.0106478 |
-0.0173581 |
-0.01755 |
| 60 |
S |
0.0564524 |
0.00215459 |
-0.0380525 |
-0.061627 |
-0.0722324 |
-0.0717536 |
-0.0585935 |
| 75 |
S |
0.0819812 |
-0.104404 |
-0.143382 |
-0.160522 |
-0.16228 |
-0.149558 |
-0.117176 |
| 90 |
S |
-0.0359008 |
-0.233591 |
-0.261294 |
-0.27086 |
-0.265409 |
-0.242333 |
-0.190523 |
| 105 |
S |
-0.203417 |
-0.33333 |
-0.356412 |
-0.367131 |
-0.364091 |
-0.340456 |
-0.276848 |
| 120 |
S |
-0.283302 |
-0.371493 |
-0.400819 |
-0.423479 |
-0.435978 |
-0.42863 |
-0.372563 |
| 135 |
S |
-0.261868 |
-0.341975 |
-0.379889 |
-0.41743 |
-0.452872 |
-0.478899 |
-0.464095 |
| 150 |
S |
-0.187517 |
-0.257346 |
-0.294901 |
-0.33715 |
-0.386582 |
-0.445469 |
-0.504932 |
| 165 |
S |
-0.095583 |
-0.137073 |
-0.160618 |
-0.189017 |
-0.22625 |
-0.281099 |
-0.379501 |
Z=48
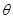 ° ° |
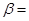 0.2 0.2 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
| 15 |
S |
-0.000354003 |
0.00179185 |
0.00163194 |
0.00120204 |
0.000743085 |
0.000345745 |
0.0000581197 |
| 30 |
S |
0.0043748 |
0.00230238 |
-0.00115705 |
-0.00367532 |
-0.00523496 |
-0.00581212 |
-0.00513253 |
| 45 |
S |
0.0122719 |
-0.0119116 |
-0.0187611 |
-0.0226723 |
-0.0241881 |
-0.0232369 |
-0.0188261 |
| 60 |
S |
-0.000775493 |
-0.0427226 |
-0.0510018 |
-0.0550211 |
-0.0553761 |
-0.0515071 |
-0.0410046 |
| 75 |
S |
-0.037162 |
-0.0831498 |
-0.0918924 |
-0.0959215 |
-0.0953098 |
-0.0885493 |
-0.0709926 |
| 90 |
S |
-0.0801096 |
-0.12314 |
-0.133128 |
-0.138642 |
-0.138991 |
-0.13141 |
-0.108084 |
| 105 |
S |
-0.111543 |
-0.152591 |
-0.165502 |
-0.174899 |
-0.179562 |
-0.175566 |
-0.151203 |
| 120 |
S |
-0.12179 |
-0.16341 |
-0.180143 |
-0.195181 |
-0.207542 |
-0.21321 |
-0.197411 |
| 135 |
S |
-0.110379 |
-0.151191 |
-0.17031 |
-0.190084 |
-0.210816 |
-0.230797 |
-0.237679 |
| 150 |
S |
-0.0822047 |
-0.116163 |
-0.133585 |
-0.153371 |
-0.177409 |
-0.208322 |
-0.24701 |
| 165 |
S |
-0.0435328 |
-0.0630519 |
-0.0735821 |
-0.0862266 |
-0.102987 |
-0.128248 |
-0.175791 |
Z=13
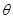 ° ° |
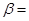 0.2 0.2 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
| 15 |
S |
0.0000289762 |
-0.000193137 |
-0.000269304 |
-0.000324673 |
-0.000355381 |
-0.000352534 |
-0.000294804 |
| 30 |
S |
-0.000789803 |
-0.00179821 |
-0.00212978 |
-0.00235565 |
-0.00244758 |
-0.00234771 |
-0.0019201 |
| 45 |
S |
-0.00300104 |
-0.00513906 |
-0.00588438 |
-0.00639987 |
-0.00660143 |
-0.00632627 |
-0.00519423 |
| 60 |
S |
-0.00627752 |
-0.00972718 |
-0.0110393 |
-0.0120076 |
-0.012464 |
-0.0120817 |
-0.0100823 |
| 75 |
S |
-0.00989484 |
-0.0147189 |
-0.0167393 |
-0.0183716 |
-0.0193562 |
-0.01916 |
-0.0164415 |
| 90 |
S |
-0.0130368 |
-0.0191377 |
-0.0219487 |
-0.024452 |
-0.0263322 |
-0.0268673 |
-0.0240351 |
| 105 |
S |
-0.0149871 |
-0.0220317 |
-0.0255784 |
-0.0290456 |
-0.0321584 |
-0.0341475 |
-0.0324057 |
| 120 |
S |
-0.015253 |
-0.0226232 |
-0.0266354 |
-0.0308998 |
-0.0353208 |
-0.0393887 |
-0.0405279 |
| 135 |
S |
-0.0136347 |
-0.0204602 |
-0.0244242 |
-0.028945 |
-0.0342038 |
-0.0403082 |
-0.0460698 |
| 150 |
S |
-0.0102474 |
-0.0155458 |
-0.0187767 |
-0.0226657 |
-0.0276005 |
-0.0343413 |
-0.0443492 |
| 165 |
S |
-0.00549471 |
-0.00839936 |
-0.0102252 |
-0.0124995 |
-0.0155491 |
-0.0201658 |
-0.029066 |
Также мы рассчитали функцию Шермана по формулам Вонга, которые он получил путем решения уравнений Дирака [5]. Они отличались от соотношений, полученных Моттом, значениями коэффициентов Dk
. Вонг пришел к выводу, что асимптотическое аналитическое выражение для сечения рассеяния в приближении малых α
совпадает с аналитическим выражением для сечения Мотта в том же приближении.
Z=80
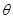 ° ° |
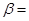 0.2 0.2 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
| 15 |
S |
-0.000325861 |
-0.000460614 |
0.001815671 |
0.00349754 |
0.00392141 |
0.00331966 |
0.00199565 |
| 30 |
S |
-0.00203191 |
0.015505 |
0.0181483 |
0.0137475 |
0.00712512 |
0.000604712 |
-0.00434351 |
| 45 |
S |
-0.00754127 |
0.0345897 |
0.0137954 |
-0.00575588 |
-0.0204759 |
-0.0297084 |
-0.0316156 |
| 60 |
S |
0.0559105 |
-0.00462725 |
-0.044347 |
-0.0693419 |
-0.0833641 |
-0.0875461 |
-0.0782605 |
| 75 |
S |
0.0754772 |
-0.104716 |
-0.142573 |
-0.162288 |
-0.169784 |
-0.165052 |
-0.140459 |
| 90 |
S |
-0.0394871 |
-0.222071 |
-0.249061 |
-0.262367 |
-0.264923 |
-0.25374 |
-0.215472 |
| 105 |
S |
-0.196093 |
-0.310419 |
-0.332176 |
-0.346143 |
-0.351742 |
-0.343136 |
-0.300442 |
| 120 |
S |
-0.269261 |
-0.342106 |
-0.367845 |
-0.390805 |
-0.409309 |
-0.416849 |
-0.388862 |
| 135 |
S |
-0.248129 |
-0.312798 |
-0.344654 |
-0.378224 |
-0.413635 |
-0.448134 |
-0.462152 |
| 150 |
S |
-0.177588 |
-0.234425 |
-0.265352 |
-0.300972 |
-0.344297 |
-0.400049 |
-0.472008 |
| 165 |
S |
-0.0905161 |
-0.124587 |
-0.143801 |
-0.167067 |
-0.197774 |
-0.243637 |
-0.329562 |
Z=48
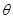 ° ° |
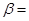 0.2 0.2 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
| 15 |
S |
-0.000279942 |
0.00177929 |
0.00171094 |
0.0013729 |
0.000945969 |
0.000497486 |
0.000075258 |
| 30 |
S |
0.0043124 |
0.00308827 |
0.000390966 |
-0.00174537 |
-0.00337733 |
-0.00448628 |
-0.00475334 |
| 45 |
S |
0.0117983 |
-0.00784188 |
-0.0131318 |
-0.0165279 |
-0.0185876 |
-0.0192257 |
-0.0173729 |
| 60 |
S |
0.000265315 |
-0.0329951 |
-0.0390729 |
-0.0425949 |
-0.044191 |
-0.0433575 |
-0.0376706 |
| 75 |
S |
-0.032362 |
-0.0666354 |
-0.0725475 |
-0.075991 |
-0.0772258 |
-0.0750157 |
-0.0649577 |
| 90 |
S |
-0.070991 |
-0.100285 |
-0.106624 |
-0.11107 |
-0.113394 |
-0.11151 |
-0.0984737 |
| 105 |
S |
-0.0994131 |
-0.125389 |
-0.133621 |
-0.140923 |
-0.146847 |
-0.148751 |
-0.137004 |
| 120 |
S |
-0.108906 |
-0.135062 |
-0.146157 |
-0.157699 |
-0.169654 |
-0.179858 |
-0.177454 |
| 135 |
S |
-0.0989384 |
-0.125479 |
-0.138621 |
-0.153744 |
-0.171929 |
-0.193331 |
-0.211078 |
| 150 |
S |
-0.0738095 |
-0.0966881 |
-0.108956 |
-0.124069 |
-0.144219 |
-0.172976 |
-0.215519 |
| 165 |
S |
-0.0391271 |
-0.0525741 |
-0.0600885 |
-0.069741 |
-0.0834847 |
-0.105635 |
-0.150263 |
Z=13
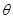 ° ° |
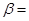 0.2 0.2 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
| 15 |
S |
0.000116029 |
0.0000599323 |
0.0000394557 |
0.000019462 |
-4.3*10-7
|
-1.92*10-5
|
-0.000033 |
| 30 |
S |
-0.000152866 |
-0.000356423 |
-0.000413753 |
-0.000464555 |
-0.000505997 |
-0.000525444 |
-0.000486041 |
| 45 |
S |
-0.00128077 |
-0.00155724 |
-0.00164009 |
-0.00171368 |
-0.0017622 |
-0.00174451 |
-0.00154729 |
| 60 |
S |
-0.00314478 |
-0.00340466 |
-0.0035158 |
-0.00362663 |
-0.00369943 |
-0.00364789 |
-0.00323359 |
| 75 |
S |
-0.00532057 |
-0.00554711 |
-0.00572068 |
-0.00592287 |
-0.00609251 |
-0.006089 |
-0.00550203 |
| 90 |
S |
-0.00729398 |
-0.00754208 |
-0.00783322 |
-0.00820998 |
-0.00860041 |
-0.00882106 |
-0.0082659 |
| 105 |
S |
-0.00859717 |
-0.00894134 |
-0.00939487 |
-0.0100208 |
-0.0107677 |
-0.0114609 |
-0.0113533 |
| 120 |
S |
-0.00889614 |
-0.00936755 |
-0.00997846 |
-0.0108623 |
-0.0120322 |
-0.0134236 |
-0.0143826 |
| 135 |
S |
-0.0080418 |
-0.00858937 |
-0.00927559 |
-0.0103079 |
-0.0117915 |
-0.0138827 |
-0.0164939 |
| 150 |
S |
-0.00608809 |
-0.0065856 |
-0.00719512 |
-0.00814112 |
-0.00959034 |
-0.0119103 |
-0.0159687 |
| 165 |
S |
-0.00327795 |
-0.0035766 |
-0.0039384 |
-0.00451165 |
-0.00542735 |
-0.00702186 |
-0.0104989 |
Также в данной работе мы сравнили экспериментальные значения функции Шермана S
(θ)
при рассеянии электронов золотом с энергиями в диапазоне от 45 до 245 кэВ на угол 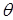 =120 =120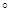 , полученные Спиваком, которые представлены в книге Мотта , со значениями, рассчитанными по Мотту и по Вонгу, и получили, что более близкими к эксперименту являются значения, рассчитанные по Вонгу. Данная функция используется в детекторах Мотта, которые в настоящее время являются основным средством для анализа поляризации электронов, поэтому необходимо уметь правильно ее рассчитывать [4].
, полученные Спиваком, которые представлены в книге Мотта , со значениями, рассчитанными по Мотту и по Вонгу, и получили, что более близкими к эксперименту являются значения, рассчитанные по Вонгу. Данная функция используется в детекторах Мотта, которые в настоящее время являются основным средством для анализа поляризации электронов, поэтому необходимо уметь правильно ее рассчитывать [4].
Результаты представлены в таблице.
Энергия электронов
кэВ
|
S(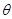 ) ) |
| экспер. знач. |
теор. знач. по Мотту |
теор. знач. по Вонгу |
| 45 |
-0,286 |
-0,364 |
-0.333 |
| 63 |
-0,337 |
-0,382 |
-0.349 |
| 83 |
-0,365 |
-0,397 |
-0.362 |
| 133 |
-0,385 |
-0,418 |
-0.3846 |
| 170 |
-0,390 |
-0,424 |
-0.395 |
| 204 |
-0,413 |
-0,427 |
-0.401 |
| 245 |
-0,411 |
-0,426 |
-0.406 |
Уверенно утверждать, что метод Вонга больше соответствует действительности, мы пока не можем, так как был рассмотрен слишком маленький экспериментальный материал. Проблема требует дальнейших исследований.
Заключение
В данной работе мы хотели выяснить, какой метод расчета функции Шермана является более точным: по формулам, полученные Моттом или Вонгом. Так как эта функция используется в детекторах Мотта, которые в настоящее время являются основным средством для анализа поляризации электронов и очень важно правильно ее подсчитывать [4].
Для сравнения мы рассмотрели экспериментальные значения, полученные Спиваком для золота и высчитанные нами численные значения функции Шермана по формулам Мотта и Вонга. В ходе этого из представленных нам ряда значений наиболее близкими к экспериментальным являются значения, рассчитанные по формулам Вонга.
Однако строго утверждать этот факт мы не можем, так как нами была рассмотрена лишь небольшая выборка значения и проблема требует дальнейшего рассмотрения.
Список литературы
1. Mott, N.F. The Solution of the Wave Equation for the Scattering of Particles by a Coulombian Centre of Force. / N.F. Mott // Proc. Roy. Soc. – 1928 A118. – P. 542-549.
2. Mott, N.F. The Scattering of Fast Electrons by Atomic Nuclei / N.F. Mott // Proc. Roy. Soc. A – 1929. – V. 124 – P. 425 – 442.
3. Sherman, N. Coulomb Scattering of Relativistic Electrons by Point Nuclei / N. Sherman // Phys. Rev. – 1956. – V. 103, № 6. – P. 1601–1607.
4. Петров, В.Н. Компактный эффективный анализатор спиновой поляризации электронов / В.Н. Петров, В.В. Гребенщиков, Б.Д. Грачев, А.С. Камочкин, М.К. Ярмаркин / Письма в ЖТФ. – 2004. – т. 30, вып. 4. – С.
5. Wong, M.K.F. Coulomb scattering of fast electrons / M.K.F. Wong // Phys. Rev.D – 1982. – V. 26, № 4. – P. 927–930.
6. Мотт, Н. Теория атомных столкновений / Н. Мотт, Г. Месси. – М. : Изд-во иностр. лит., 1969. – 756 с.
|